Термодинамические методы получения определяющих соотношений

Common questions of classical and modern thermodynamics considered. The description is given concepts quasi-static process, elasticity, viscosity, plasticity. The basic corollaries of the second and third laws of thermodynamics are parsed. Common relations of a thermoelasticity are given. The bases and a methodology of existing thermodynamic approaches to obtaining defining relation of the viscoelastic and plastic materials are full enough elucidated. Ways of elimination of paradox of the infinite speed of heat distribution are indicated.

Основная задача термодинамики сплошных сред состоит в установлении определяющих соотношений, позволяющих воспроизводить результаты опытов, которые существующими средствами не описываются вообще или же описываются, но недостаточно точно. В настоящее время считается возможным применение нескольких подходов к термодинамическому описанию поведения материалов. Отличаются они, главным образом, физической интерпретацией второго начала термодинамики. В одних подходах используются представления о неравновесной энтропии и неравновесной температуре, в других подходах – нет. В рамках каждого подхода допускаются различия в выборе параметров состояния среды. Указанные отличия существенным образом влияют на конечный результат (определяющие соотношения).

Общие положения и основные понятия

По отношению к актуальной и отсчётной конфигурациям среды изменение массы и внутренней энергии описывается уравнениями [ 1-3 ]

р + pV• v = 0, р о /р = det F ,                             (1)

р e = -V- j q + рР + T:D , Р о e = -V , • J q +р о в + P:C .                (2)

Здесь р , р ₀ - плотность в актуальной и отсчётной конфигурации, v - скорость, F = d x ( t , X )/5 X - градиент деформации ( x ( t , X ) - закон движения среды, x , X -радиус-векторы одной и той же точки среды в отсчётной и актуальной конфигурациях), e - удельная внутренняя энергия, j q - (истинный) вектор теплового потока, р -плотность внешних источников теплоты (например, за счёт излучения), T – (истинный) тензор напряжений, D = 0,5 ( V v + V v T ) - тензор скоростей деформации ( V = d" x , V _X д д \ - операторы градиента по отношению к актуальной и отсчётной конфигурации),

J , = ( р о /p ) F - 1 • j q , P = (V 2 )( Р о /р>^{- 1} • т - ( f ^{- 1} ) T , C = F T • F              (3)

– приведённый вектор теплового потока, приведённый тензор напряжений, мера деформации Коши соответственно. Величины (3) удовлетворяют равенствам

Р о ¹ J q • G = p^{- 1} j q • g , р о ¹ Р:(2 = p^{- 1} T:D , E = 0,5 ( C - 1 ) ,                 (4)

Общие вопросы неравновесной термодинамики где g = V6, G = VX6 = g • F - градиент абсолютной температуры 6 по отношению к актуальной и отсчётной конфигурации, E – тензор конечной деформации, I – единичный тензор. По теореме об изменении кинетической энергии индивидуального объёма среды V , ограниченного поверхностью 2 с внешней нормалью n [4], d jpv- dV = j v • T • nd2 + j pb • vdV - j T : DdV .            (5)

^dt V ²         2              v           v

Здесь b – плотность внешних массовых сил (например, сил тяжести). Количество теплоты, подводимое к индивидуальному объёму среды от внешних источников в единицу времени, определяется выражением

Q ext =— j j q • П d E + j pp dV .

С учётом (3) соотношения (5), (6) можно представить в локальной форме записи:

k = aext + aint, k = v2/2, aext =p-1V-(v• T) + b • v , aint = -p-1T : D, (7) q ext =-p-1V-jq +в = -р01Vx • Jq +в.(8)

Здесь a & ^ext , a & ^int – удельные мощности внешних и внутренних сил, k – удельная кинетическая энергия, q & ^ext – удельная скорость подвода внешней теплоты.

Интегральное уравнение баланса некоторой скалярной величины A имеет вид d jpAdV = -j jA • nd2 + jpcAvdV + jpcAdV,(9)

dt V           2           VV где jA - вектор потока, cAxt - приток от внешних источников, cA - производство величины A . Ссылаясь на (1), по теореме Гаусса – Остроградского из (9) находим

РA + V j A -PcAxt =рсТ, p о A + V x • J A -p о c Axt =Po c A1, J A =(Po/p)F-1 •j A .

Первое уравнение (10) относится к актуальной конфигурации, а второе уравнение (с приведённым вектором потока J _A ) – к отсчётной конфигурации среды.

Классическая термодинамика равновесных процессов (ТРП)

В ТРП (термостатике) центральное место занимает представление о равновесном состоянии термодинамической системы (точек среды). Понятие состояния точки среды отождествляется с некоторым набором параметров П = ( П 1 , П ₂ ,. „) . Число и тип параметров состояния устанавливаются на основании опытных данных. Под термомеханической (термодеформационной или простой) системой понимается такая термодинамическая (макроскопическая) система, в которой могут протекать только процессы деформирования и теплообмена [ 5 ] . Равновесное состояние каждой точки термомеханической системы характеризуется набором параметров состояния П = ( Э , F ) , где Э - эмпирическая температура. Существование равновесного состояния обеспечивается принятием общего начала термодинамики: «изолированная макроскопическая система с течением времени приходит в состояние термодинамического равновесия и никогда самопроизвольно выйти из него не может» [ 6 ] . Термомеханическая система считается изолированной, если её граница не деформируется и не проводит теплоту (адиабатическая изоляция). Эмпирическая температура измеряется термометром той или иной конструкции и рассматривается как «мера нагретости» материальных тел. В состоянии термодинамического равновесия эмпирическая температура всех точек термомеханической системы имеет одинаковое значение (нулевое начало термодинамики [ 7 ] ). Обычно в ТРП рассматриваются термомеханические системы, находящиеся в однородном деформированном состоянии.

Общие вопросы неравновесной термодинамики

Чтобы удовлетворить данному требованию, в качестве термомеханической системы можно взять некоторый достаточно малый объём среды.

Замечание . Иногда высказывается мнение, что эмпирическая температура является термодинамически равновесным параметром, который строго применим только для систем, находящихся в термодинамическом равновесии. Такое представление восходит к Фаулеру и Гуггенгейму, которые для единообразного изложения термостатики (каждое из начал термодинамики – первое, второе и нулевое – должно приводить к доказательству существования новой функции состояния – энергии, энтропии и температуры) изначально ограничивают область применимости всех результатов одними равновесными процессами. Если исходить из работ Кельвина [ 7 ] , то понятия «эмпирическая температура» и «мера нагретости» следует рассматривать как эквивалентные первичные понятия. Не вызывает сомнений, что различие в степени нагретости присуще точкам среды в любых условиях. Поэтому факт существования эмпирической температуры, как меры нагретости, не подлежит сомнению. Если преследовать чисто прагматические цели (создаваемая термодинамическая теория должна давать приемлемое совпадение теоретических и экспериментальных данных), то вовсе не обязательно знать, что такое мера нагретости как философская категория. Достаточно уметь правильно пользоваться данным понятием. В свою очередь, чтобы правильно применять понятие эмпирической температуры, следует ответить, как минимум, на два вопроса: 1) сколько чисел надо поставить в соответствие мере нагретости, 2) как эти числа преобразуются при замене системы отсчёта. Если исходить из существующих способов измерения эмпирической температуры с помощью термометров, которые применяются при экспериментальном исследовании равновесных и неравновесных процессов, то можно утверждать, что в любых условиях эмпирическая температура является инвариантной скалярной величиной (в каждой точке среды эмпирическая температура задаётся одним числом, одинаковым во всех системах отсчёта). Для этого надо чётко обговорить процедуру измерения эмпирической температуры посредством того или иного термометра, ибо эмпирическая температура – это то и только то, что измеряется термометром.

В ТРП важное место занимает представление о равновесных и обратимых процессах. Термодинамический процесс называется равновесным или квазистатическим, если все параметры системы изменяются физически бесконечно медленно, так что система всё время находится в равновесных состояниях [ 6 ] . Конечно, реально осуществить такой процесс невозможно; ему также нельзя дать и непротиворечивое объяснение. Действительно, с одной стороны, равновесный процесс должен состоять из ряда чередующихся во времени состояний равновесия, а, с другой стороны, переход из одного состояния равновесия в другое возможен лишь в результате нарушения этого равновесия (общее начало термодинамики). Поэтому трудность усвоения данного понятия связана с высокой степенью абстракции [ 8 ] . Обратимым процессом называют такой процесс, который может совершаться в обратном направлении так, что система пройдёт все те же состояния, что и при прямом процессе, но в обратном порядке [ 9 ] . Данное понятие также требует разъяснения. Например, в двух аксиоматических теориях, предложенных в своё время Дьярмати и Ландсбергом как прямое развитие термодинамического подхода Каратеодори, встречаются два в точности противоположных утверждения: «квазистатический процесс может быть как обратимым, так и необратимым» (Дьярмати) и «любой квазистатический процесс обратим и наоборот» (Ландсберг) [ 10 ] . С Дьярмати солидарен Л.И. Седов [ 4 ] , а с Ландсбергом -М. А. Леонтович [ 9 ] . Чтобы примирить эти две точки зрения, надо уточнить качественные отличия между упругостью, вязкостью и пластичностью.

Общие вопросы неравновесной термодинамики

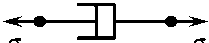
Обратимся к реологическим моделям идеально упругого, идеально вязкого и идеально пластического элементов (рисунок), которые подчиняются закону Гука о = E s , закону вязкости Ньютона а = це и закону сухого трения Кулона - Амонтона о = о ₅ е/|s| ( E , ц , о ₅ = const >  0) соответственно [ 11 ] . Равновесие упругого элемента имеет место при любой постоянной нагрузке о ; после снятия нагрузки он восстанавливает свою длину. Равновесие вязкого элемента возможно только при нулевой нагрузке; после снятия нагрузки о * 0 вязкий элемент приобретает остаточную деформацию. Равновесие пластического элемента возможно, если |о| < о ₅ ; он деформируется, если |о| > о ₅ ; после снятия нагрузки пластический элемент также приобретает остаточную деформацию. Как видим, наличие (или отсутствие) остаточной деформации является отличительным признаком лишь при сравнении упругого элемента с вязким и пластическим элементами; для сравнения вязкого и пластического элементов нужен другой критерий. С этой целью рассмотрим модели вязкоупругих тел Фойгта, Максвелла и вязкопластического тела Бингема (см. рисунок). При равновесии тела Фойгта выполняется равенство о = E s . Поэтому в ходе процесса, который можно считать квазистатическим, скорость деформирования должна быть такой, при которой усилие, развиваемое вязким элементом, было бы пренебрежимо мало по сравнению с усилием, развиваемым упругом элементом, |цс| <<  E s| . Когда ц >>  1, скорость деформирования тела Фойгта может быть очень малой величиной, |s| = |о|/ц <<  1. Однако если E s - цS| >  E s|5 , где 5 - некоторое достаточно малое число, то процесс деформирования не будет квазистатическим; его следует рассматривать как процесс ползучего течения, при котором можно пренебречь силами инерции, но нельзя пренебречь силами вязкости. Аналогичным образом, если при приложении нагрузки о выполняется требование |ps| <<  E е| , то процесс деформирования тела Максвелла можно считать квазистатическим; в противном случае процесс деформирования не квазистатический, даже если |s| = Ю/ц<< 1. Причины необходимости такого разграничения в ТРП предельно просты: квазистатические процессы нужны для того, чтобы можно было пренебречь работой сил вязкости по сравнению с работой сил упругости. Принципиальное отличие между вязким и пластическим элементом наглядно иллюстрируется на модели тела Бингема (рисунок, е ). Какой бы ни была скорость деформирования s , пластический элемент всегда развивает одно и то же усилие; усилие, развиваемое вязким элементом, убывает по величине при уменьшении скорости деформирования.

E

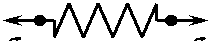
а

ц

б

• >

о о

в

ц

E

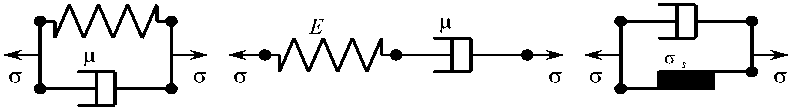
г                         д                           е

Рис.1. Реологические модели: а – упругий элемент, б – вязкий элемент, в – пластический элемент, г – тело Фойгта, д – тело Максвелла, е – тело Бингема

Общие вопросы неравновесной термодинамики

Таким образом, под упругостью в чистом виде можно понимать свойство материальных тел сопротивляться деформации, которое приводит к восстановлению их первоначальной формы после снятия внешних нагрузок. Под вязкостью можно понимать свойство материалов сопротивляться деформации, которое проявляется в динамических процессах и исчезает (не наблюдается) в квазистатических процессах. Наконец, под пластичностью можно понимать свойство материалов сопротивляться деформации, которое проявляется в квазистатических и динамических процессах в равной степени. Тогда, если материал обладает вязкоупругими свойствами, то «любой квазистатический процесс обратим и наоборот» (Ландсберг, Леонтович). Если же в одной области изменения параметров материал обладает вязкоупругими свойствами, а в другой области – вязкоупругопластическими свойствами, то тогда «квазистатический процесс может быть как обратимым, так и необратимым» (Дьярмати, Седов).

В ТРП полагается, что все квазистатические процессы обратимы. Поэтому объектом исследования в ТРП являются вязкоупругие материалы (газы, жидкости, твёрдые тела с ярко выраженным пределом текучести). Распространение большинства результатов ТРП на пластические среды возможно только через обобщение.

В термодинамике Клаузиуса – Кельвина под первым началом понимается принцип эквивалентности между теплотой и работой: «во всех случаях, когда из теплоты появляется работа, тратится пропорциональное полученной работе количество тепла, и, наоборот, при затрате той же работы получается то же количество теплоты» [ 12 ] . Иными словами, если термодинамическая система совершила круговой процесс (по окончании процесса все точки системы вернулись в начальное термодинамическое состояние), то тогда [ 4 ]

j ( dQ ^ext + dA ^ext ) = 0. (11)

Соотношение (11) справедливо для любых круговых процессов. Для равновесных процессов, протекающих в бесконечно малом индивидуальном объёме среды, dqext = c(3, C)d3 + p01L(3, C): dC , daext =-daint = p-1P(3, C): dC, (12) где c – удельная теплоёмкость при постоянной деформации, L – тензор теплот изотермического деформирования. По своему виду первая формула (12) отличается от (8); её справедливость основывается на физическом положении, которое широко использовалось в термометрии задолго до Клаузиуса и Кельвина: «если термодинамическую систему подвергнуть внешнему воздействию, то у неё должен измениться хотя бы один из параметров состояния». Вторая формула (12) вытекает из теоремы (7) с учётом (4). Обе формулы (12) записаны в сопутствующей системе координат, относительно которой данная точка среды неподвижна, а её бесконечно малая окрестность деформируется без квазитвёрдого вращения. Это допустимо, так как величины dqext , daint не зависят от выбора системы отсчёта [13]. На основании (11), (12) имеем

J (dqext + daext )= J {c(3, C)d3 + p--1 [L(3, C) + P(3, C)]: dc} = 0.

Поскольку параметры (3, C) могут принимать независимые приращения во всей области своего изменения, приходим к выводу о существовании функции состояния e(3,C), называемой удельной внутренней энергией. Для квазистатических процессов de(3, C) = c(3, C)d3 + p--1 [l(3,C) + p(3,C)]: dC = dqext + daext. (13)

Под вторым началом в ТРП понимается постулат Кельвина или постулат Клаузиуса (они эквивалентны [ 14 ] ). Согласно постулату Кельвина «нельзя построить периодически действующую тепловую машину, единственным результатом которой было бы производство работы за счёт охлаждения одного теплового резервуара». Физическая интерпретация постулата Кельвина предельно ясна. Если такую машину

Общие вопросы неравновесной термодинамики можно было бы создать, то тогда, поместив её, например, в океан, можно было бы за счёт охлаждения воды производить работу, например, вращать вал генератора и вырабатывать электрическую энергию, которая передавалась бы на материк, использовалась для бытовых и промышленных нужд, а затем, после превращения в теплоту, вновь возвращалась в океан. По своей значимости такая машина ничем не уступает perpetuum mobile. Поэтому-то её и нельзя построить.

Из постулата Кельвина вытекает, что дифференциальная форма (12) для dq ^ext имеет интегрирующий множитель, зависящий от эмпирической температуры [ 6, 14 ] :

c ( Э , C ) d Э + р^{- 1} L ( O , C ) : d C = 0 ( Э ) d п ( Э , C ) .                      (14)

Поскольку 0 ( э ) является отличной от нуля монотонной функцией, её можно взять в качестве новой эмпирической температуры. Если в одном из фиксированных состояний приписать величине 0 положительное значение, то она станет абсолютной температурой, а величина п - удельной энтропией (энтропией Клаузиуса). Причём, если до этого эмпирическая температура 0 определялась по идеально-газовому термометру, то тогда будет выполняться равенство

0(э)=Э .(15)

Совместно (13) – (15) приводят к уравнению Клаузиуса

0dп(0,C) = de(0,C)-p01P(0,с): dC .(16)

И хотя уравнение (16) получено при рассмотрении равновесных процессов, оно справедливо для любых неравновесных состояний вязкоупругих сред [ 13 ] .

Из второго начала термодинамики вытекает также неравенство Клаузиуса [ 14 ]

Н2 -Н1 >JdQext /0ext, Н = |рпdV.(17)

V

Здесь Н 1 , Н 2 - энтропия индивидуального объема среды V в некоторых равновесных состояниях 1 и 2, dQ ^ext – количество теплоты, сообщаемое этому объёму одним из тепловых резервуаров с температурой 0 ^ext. Знак равенства в (17) отвечает равновесному переходу из состояния 1 в состояние 2, а знак неравенства – неравновесному переходу. Количество тепловых резервуаров (материальных тел, которые могут обмениваться теплотой без совершения работы) полагается достаточно большим, чтобы обеспечить протекание указанного перехода. Температура 0 ^ext - это температура, которую имеет данный тепловой резервуар (обязательно бесконечной массы) не во время взаимодействия с объёмом среды V , а в состоянии равновесия до и после их теплового контакта [ 14 ] . Поэтому 0 ^ext является фиксированным числом, имеющим в лучшем случае косвенное отношение к распределению температуры на данном участке границы выделенного объёма среды.

Ещё одно неравенство устанавливается из постулата Клаузиуса: «теплота не может самопроизвольно переходить от тела, менее нагретого, к телу, более нагретому». Возьмём два тепловых резервуара большой массы с разными температурами. Передачу теплоты осуществим посредством процесса теплопроводности через тонкий стержень с адиабатически изолированной боковой поверхностью. При в = 0 и установившемся режиме теплопроводности по формуле (6) через каждое плоское сечение стержня в единицу времени будет проходить одинаковое количество теплоты. Если взять сечение с нормалью, направленной по градиенту температуры V0 в центре сечения, то тогда на основании постулата Клаузиуса можно записать неравенство Фурье с ограничениями:

• - j q -veL0 ( t , x y₅ 1 = o >  o.                                          (18)

• ¹    v ( t , x ) = 0

Общие вопросы неравновесной термодинамики

Ограничения на стационарность температурного поля и неподвижность среды являются существенными. В общем случае при неустановившемся режиме теплопроводности в формуле (6) скорость подвода теплоты к любому объёму стержня Q ext * 0. Поэтому снять ограничения в (18) не представляется возможным, поскольку требование постулата Клаузиуса Q ( t ) >  0 ( Q - количество теплоты, полученное тепловым резервуаром с меньшей температурой) не исключает возможности того, что в некоторые моменты времени Q ( t ) <  0.

По третьему началу термодинамики («по мере приближения абсолютной температуры к нулю энтропия всякой равновесной системы при изотермических процессах перестаёт зависеть от каких-либо термодинамических параметров» [ 6 ] )

5р(0 = 0, C)/5C = 0.(19)

Это позволяет сузить класс функций P(0,C) [15]. Согласно (13) - (15) можно записать c (0, C) = 5 e (0, C)/50 = 05ц(0, C)/50.(20)

Проинтегрировав (20), на основании (19) получим

e ( 0 , C ) = J c ( 0 , C ) d 0 + e h ( C ) , n ( 0 , C ) = J 0^{- 1} c ( 0 , C ) d 0 + const, 00

где e h ( c ) - внутренняя энергия при нуле абсолютной температуры. Так как энтропия определена с точностью до аддитивной постоянной, то, приписав последней нулевое значение, получим следующее выражение для свободной энергии:

f ( 0 , C ) = e ( 0 , C ) - 0ц ( 0 , C ) = J ( 1 - 0/0' ) c ( 0' , C ) d 0' + e h ( c ) .

По уравнению Клаузиуса (16)

df ( 0 , C ) = -n ( 0 , C ) d 0 + p ₀ ¹ P ( 0 , C ) : d C , p^{- 1} P ( 0 , C ) = f ( 0 , C )/ d C , n ( 0 , C ) = -5 f ( 0 , C )/ 50 .

Отсюда находим

⁰°, P ( 0 , C ) = p 0 d e h ( c )/ d C + J ( 1 -0/0' ) d c ( 0' , C )/ d C d 0' . _                     0                                       _

Величину e h ( c ) можно рассматривать как гиперупругую составляющую внутренней

(свободной) энергии. Если теплоёмкость зависит только от температуры (в частности, постоянна), то из (21) вытекает, что P = P(c) . Иными словами, при c = c(0) материал является гиперупругим [2, 3]. При малых деформациях и малых изменениях температуры из (21) следует уравнение состояния Дюамеля - Неймана [15]:

T = [ - p ₀ -y ( 0-0 ₀ ) +X tr ] I + 2 ц .                      (22)

Здесь в - линейный тензор деформации, X и ц - упругие постоянные Ламе, у -коэффициент температурных напряжений, 0 ₀ и p ₀ - температура и давление окружающей среды в отсчётной неискажённой конфигурации (например, температура 0 ₀ - комнатная, а давление p ₀ - атмосферное).

Классическая (линейная) термодинамика необратимых процессов (ТНП)

В ТНП используются результаты ТРП, в частности, уравнение Клаузиуса (16). Понятия неравновесной энтропии и неравновесной температуры не привлекаются, но учитывается тот факт, что при протекании неравновесных процессов приведённый тензор напряжений P не равен своему равновесному значению P ' ( 0 , C ) , входящему в (16),

P = P ' + P" .                                       (23)

Общие вопросы неравновесной термодинамики

Величины P ' , P" будем называть статической и динамической составляющими приведённого тензора напряжений P . То же самое относится к разложению T = T + T" истинного тензора напряжений T на составляющие T , T , которые связаны с P ‘ , P" соотношениями, аналогичными второму соотношению (3). В состоянии равновесия P" = 0, T = 0 . В ТНП величина T" называется тензором вязких напряжений.

Из уравнения Клаузиуса (16) и уравнения для внутренней энергии (2) имеем

РП = р ej 0 - ( p/Р о ) P ‘ :C /0 = - ( v • j q )/ 0 + рР/О + ( p/Р о )( P - P ‘ ) : С /о .

С учётом разложения (23) совместно со вторым равенством (4) получаем

РП + V • ( j , /о) - pp/0 = - j q ■ g/ 0 2 + T: D/ 0 .                   (24)

Сопоставив (24) с общим уравнением баланса (10), можно принять j„ = jq /0, О“ =р/о, Р< =- jq • g/02 + T":D/0.           (25)

Следуя формализму Онзагера [16], будем рассматривать величины jq, T" как термодинамические потоки, а величины - g/02 = V0-1, D/0 - как термодинамические силы. Тогда с учётом соотношений взаимности Онзагера из (25) получим формулы jq = -Lq • g/02 + L q : D/0, T = Lq • g/02 + Lp : D/0, которые справедливы при небольших отклонениях от равновесного состояния. Поэтому D = г . Кинетические коэффициенты Lq , L q , Lp являются постоянными тензорами второго, третьего и четвёртого ранга соответственно. Для изотропных материалов по принципу Кюри «никакая термодинамическая сила не может вызвать термодинамического потока, имеющего другую тензорную размерность» [16]. Поэтому L‘q = 0 и jq = -Lq • g/02, T = Lp :D/0.(26)

С другой стороны, по принципу объективности поведения материалов (см., например, [2, 10]) в линейном приближении по неравновесным параметрам g , D имеем jq (0,g) = -Л(о)g , T-(0,D) = Xv(0)trDI + 2цv (0)D .(27)

Сравнив (26), (27), получаем

Lq = 02Л(0)1, Lp = 0[Xv(0)Ci + цv(0/Cn + C„)],(28)

где C I , C II , C III - изотропные тензоры четвёртого ранга [ 2 ] . Для твёрдых тел динамическая составляющая тензора напряжений (27) подчиняется закону Навье – Стокса, как для жидких и газообразных сред. Из условия ст ¹^ >  0 следует, что

Л ( 0 ) > 0, X v ( 0 ) > 0, ц v ( 0 ) > 0.

Таким образом, из (22), (27) для вязкоупругих твёрдых тел имеем

T = T ' + T" = [ - p ₀ -у ( о-О ₀ ) +Xta ] l + 2 ц г + X _v ( о )йЯ + 2 ц _v ( о ) ё , j _q =-Л ( 0 ) V0 .

На основании (2), (20) получается классическое уравнение теплопроводности

Р c d0/d t = ЛV ² 0 + Рр ,                                (29)

записанное для неподвижной среды с постоянным коэффициентом теплопроводности Л . Уравнение (29) является уравнением параболического типа. Поэтому скорость распространения теплоты принимает бесконечное значение, что неприемлемо с физической точки зрения (тепловой парадокс). Впервые на данную особенность обратил внимание ещё Максвелл [ 10 ] . Чтобы уравнение (29) стало гиперболическим, в него надо внести соответствующие изменения, которые в общем случае могут затронуть левую и (или) правую его части. Эти изменения требуют либо замены классического выражения для внутренней энергии, либо отказа от закона Фурье. В первом случае механизм тепловой инерции будет носить объёмный характер, а во

Общие вопросы неравновесной термодинамики втором случае – диффузионный характер. Вопрос о том, какой именно механизм тепловой инерции реализуется в природе, в настоящее время является открытым.

Термодинамика необратимых процессов с неравновесной температурой (ТНПНТ)

Несколько другой подход был предложен Мейкснером [17]. Стремясь к построению локально-неравновесной термодинамики, он не склонен допускать существования неравновесной энтропии, ссылаясь при этом на слова Кирхгофа: «… понятие энтропии, которая может быть измерена, а следовательно, и определена только в обратимых процессах, не применимо к необратимым процессам» (цитируется по [18]). Из равновесной термодинамики берётся уравнение Клаузиуса (16) и постулируется диссипативное неравенство рП +V.(jq/о)-рр/О = ра"' >0, (30) обобщающее аналогичное неравенство ТНП. Здесь p(e,С) - энтропия Клаузиуса, О - неравновесная температура, которая при термодинамическом равновесии совпадает с абсолютной температурой: Оeq=0. ТНПНТ отличается от ТНП в одном важном пункте: в (30) используется не абсолютная температура 0 , а неравновесная температура О .

Если выразить из (2), (16) величины ( -V- j _q +рв ) , П и подставить результат в (30), то с учётом (4) получится следующее выражение для производства энтропии:

аint = (1/0-1/0)e + (р/0- P‘/0):С -(vo/O2). Jq > 0.            (31)

Используя формализм Онзагера и рассматривая в (31) величины, стоящие в скобках, как термодинамические потоки, а множители при них — как термодинамические силы, придём к следующим определяющим соотношениям:

1 0- 10 = L e e , -v0 /0² = L _q • J _q , p/ 0 - P '/0 = L P :C .         (32)

При записи (32) был принят во внимание принцип Кюри для изотропных сред. Для них кинетические коэффициенты L _q , L _P подобны (28):

L q =A- ' I , L P = X . C i +p ,. ( C„ + C„ ) .

В результате получаем

0 = 0/(1 - 0Lee) = 0 + 02Lee, Jq = Лv(V0), P = 0(p'/0+X.trC1 + 2p.С).

Статическая составляющая тензора напряжений P ' определяется формулой (21). Для замыкания уравнений состояния (32) нужно задать определяющее соотношение для внутренней энергии. Например, можно ограничиться равновесной зависимостью e ( О , С ) . Тогда для неподвижной среды будем иметь

de(О,С)/5О = c(О,С), e = c0, 0 = 0/(1 -ОLecО)=0 + cLeО2О.

Как видим, в данном случае неравновесная температура зависит от скорости изменения абсолютной температуры, 0 = 0 ( о , 0 ) . Поэтому уравнение теплопроводности содержит старшую производную V ² 0 и является уравнением параболического типа.

Расширенная необратимая термодинамика

Основы расширенной необратимой термодинамики (РНТ) разработаны немецким учёным Инго Мюллером. В отличие от ТНПНТ в РНТ предполагается существование неравновесной энтропии П , которая при термодинамическом равновесии совпадает с энтропией Клаузиуса р . Понятие неравновесной температуры в РНТ не используется. При разработке этой локально-неравновесной теории одновременно применяется

Общие вопросы неравновесной термодинамики кинетический и феноменологический подходы. Поэтому в монографии [19] рассмотрение ограничивается случаем разреженных газов.

Чтобы вместе охватить твёрдые, жидкие и газообразные среды, положим, что неравновесная энтропия n является функцией внутренней энергии e, градиента деформации F , вектора теплового потока jq и динамической составляющей истинного тензора напряжений T": n = р(e, F, jq, T"). С помощью принципа объективности поведения материалов можно показать, что неравновесная энтропия имеет вид

П = П(e, C, Jq , P") и является изотропной скалярной функцией. Поэтому в общем случае n = n (e, trC, trC2, trC3, trP", trP''2, trP"3, J 2,

q(33)

P " :C , P" ² :C , P " :C ² , P" ² :C ² , J q - C - J q , J q - C ² - J q , J q - P" . J q , J q - P" 2 - J q ) .

При термодинамическом равновесии J _q = 0, P" = 0 и П ( e , C , J q = 0 , P" = 0 ) = n ( e , C ) .

Введём в рассмотрение тензор

P" = P"-(P" :C)C-1/3.(34)

Согласно определениям (3)

F -P".FT =(po/p)T"/2, P" :C = (po/p)trTV2,(35)

где T" - девиатор динамической составляющей истинного тензора напряжений. Как видим, тензор (34) является аналогом девиатора T", а скаляр в (35) - аналогом следа trT". Исходя из этого, представим зависимость (33) квадратичным приближением

П = n(e,C)- a1(P": C)2 - a2P'': P'' - a3J2 ,(36)

где a i - некоторые константы. По уравнению Клаузиуса (16)

( а _л/ з e ) , = V e , ( an/S C ) o = -p »¹ p'^ ,

где P ' - статическая составляющая приведённого тензора напряжений (21). На основании (36), (37) с учётом (2), (4), (23) находим pon = p0Ие - P': С/е -2poa1(P": C)(P": C) - 2p„a2P": l>' - 2p a Jq • -Jq = -V, • (j,/e)- (38) - Jq ■ G/e2 + p„p/e + P-: C/e - 2poa1(p-: C)(P-: €)■ - 2poa2p': P" - 2poa3Jq ■ .J,.

Чтобы отделить объёмную деформацию от деформации изменения формы, воспользуемся приёмом, предложенным В.А. Пальмовым [ 20 ] ,

C = 13 (C)C+, где 13 (c) = detC = (p0/p)2 - третий главный инвариант меры деформации Коши. Тогда

P ' :C = P ' : C ₊ 1₃ + 1 ₃ P ' : (3 ₊ = ( P": C )(_J & ₃/ / ₃ + 1 ₃ C ^{- 1} : (3 ₊ /3 ) + 1 ₃P" : (3 ₊ .         (39)

Сопоставив (40) с общим уравнением баланса (10), можно предположить, что jn= Jq/e, a“t =₽/e, a nnt =(P":C)[I3/(p 0 e13) +13 C-1 :C+/(3p „ e)-2a| (P":C)']-

• - J q - [g/ '(p 0 e ² ) + 2 a 3 .J q ] + P-: [ 1 3 C +/( p 0 e ) - 2 a 2 P ' ] .

Общие вопросы неравновесной термодинамики

Соотношения (41), (42) записаны по отношению к отсчётной конфигурации среды. Для выполнения требования о“t >  0 достаточно принять соотношения

( P" :С ) = K v \&з /( р о б I з ) + I з С ^{- 1} :С ₊/ ( 3 р о б ) - 2 а 1 ( P" :C ) ^ j , J q =-л [ б/ ( р о © ² ) + 2 а з ^ q ] ,

P" = \ X v C i + p v ( Си + С_ш ) ] : \ l 3 С ₊/ ( р о б ) - 2 а 2 P ’] =

X v \ l 3И С +/ ( р о б ) - 2 a 2 tr P" ] l + 2 p v \ l 3 С +/ ( р о б ) - 2 a 2 P"

при условии, что материальные параметры Kv, Л, X v, рv являются положительными функциями б, С. Соотношения (43), (44) предназначены для описания изотропных вязкоупругих сред. При переходе от приведённых величин Jq, P" к истинным величинам jq , T" надо учесть (1), (3) и известные равенства F 1 • F = I, Vv = F • F 1, С = 2FT • D • F . В результате совместно с (21) , (23) будем иметь

T = T + T, Т = 2(р/ро)F• P(б,С)FT = Т(б,B), T = T" + trT"I/3, (45) - \V(2a1 K)]trT = \1 - 2р/(зр0a1б)]v • v + trT",(46)

• - W ( 4 a 2 P v ) ] T ' = \ x v р/^р v р 0 б ) ] \ tr ( B • D ) - ( V • v ) tr B ] B +

+ \Xv/(2рv )]B-1 : \t" + (V • v)T" - Vv • T" - T” • VvT ]b -

• - \ 2р/ ( а 2 р 2 © ) ]\ в • D • B - ( V • v ) B ² ] + \t" + ( V • v ) T" - V v • T” - T" • V v ^T ] ,

1 (2а3Л)]jq = -\р/(2а3Pо©2 )]b • V© - \djq^t + (V • v)jq - Vv • jq ].(48)

Здесь B = F • FT – мера деформации Грина. Для замыкания системы определяющих соотношений (45) – (48) нужно определяющее соотношение для внутренней энергии. С этой целью можно взять, например, равновесную зависимость е(б,С), считая, что она справедлива и в неравновесных условиях. В этом случае для неподвижной среды согласно (2), (48) будет иметь место система уравнений рcйб/аt = -V • jq + рв, [р/(2aзЛ)]jq = -|р/(2а3б2)]v6 -djq/31, которая аналогична системе уравнений Максвелла - Каттанео - Лыкова \21]. Поэтому уравнение теплопроводности имеет гиперболический тип, и распространение тепловых возмущений происходит с конечной скоростью.

На основании (10) приведённому вектору потока неравновесной энтропии (41) отвечает истинный вектор потока неравновесной энтропии j ^ = j _q /б. Данное значение было принято по аналогии с (25). В этом случае J п = J п ( б , J _q ) или, что то же самое, J п = J п ( е , С , J _q ) . Данный факт не согласуется с принципом равноприсутствия, согласно которому «выбирая для изучения некоторый допустимый класс определяющих соотношений, теоретик должен выбирать для всех этих соотношений одни и те же независимые переменные» \ 3 ] . Поэтому приведённый вектор потока неравновесной энтропии в общем случае должен быть функцией такого же вида, как и неравновесная энтропия: J п = J п ( е , С , J _q , P" ) . Чтобы учесть данное обстоятельство, можно вместо (41)

взять, например, следующее выражение:

J п = J q /б + Д , ( P " :C ) J q +Д 2 P" . J q .                     (49)

Вопрос о том, равны нулю константы Д 1 , Д ₂ или нет, следует решать посредством последующей экспериментальной проверки получаемых определяющих соотношений. Кстати, именно так исторически развивалась ТНП. Законы Фурье, Фика, Навье –

Общие вопросы неравновесной термодинамики

Стокса, Ома и т.п. были экспериментально установлены задолго до создания ТНП. Более того, именно опыты Фойгта по анизотропной теплопроводности (наряду с другими фактами), проведённые в 1903 г., привели Онзагера в 1931 г. к его соотношениям взаимности (подробнее см., например, [ 22 ] ).

Примем значение (49), сохранив прежней величину ст ^ xt = P/O . После этого шага следует вернуться к уравнению (40) и добавить к его левой и правой частям слагаемое

V л ‘[ A ( P*:CJ q +А , F" - J q ] = A 1 [ ( P " :C ) V _A . J q + J q -V _A ( P ' :C ) ] + A ₂ [ P-: V _A J q + J q ' ( v , ■ P " )] .

В результате будем иметь

P o n + V Л -J , /O + A l (p" : CJ q + A 2 P' - J q ] -p o ₽/O =

= P o ( P":C ) [ / 3 /( P o e 1 3 ) + 1 3 C ^{- 1} : C +/ ( 3 p o O ) - 2 a , ( P":C )' + ( A , /p o ) V _A - J , ] -

-P o J q -G/ ( p o e ² ) + 2 a 3 J q + ( A , /P o ) V , ( P':C ) + ( A 2 /p o ) V , - P " ] +

+ P o P': [ l 3 C + /GVO- 2 a 2 P " + ( a 2/po )V _A J q ]

Отсюда вытекает уточнённое выражение для производства неравновесной энтропии ст“ = (P': C)/ /(po013)+13 C- : C + /(3poO)- 2a, (P': C)" + (A, /po )V A - J q ]-

• - J q -[ G/ ( p o 0 ² ) + 2 a 3 J q + ( A , /p o ) V , ( P " :C ) + ( A 2 /p o ) V _A - P' ] +

+ P " : I 3 C +/ ( p o 0 ) - 2 a 2 P' + ( A 2/po ) V _A J q ^]

и отвечающие ему определяющие соотношения ( A ^s – симметричная часть тензора A )

P":C = K,[/3/(poO13)+13C-1 :C+/(3p„9)-2a,(P':C)-+(A,/p„)VA ■ Jq],(5o)

Jq =-a[g/(poO2)+ 2a3Jq +(A,/Po)VA(P-:C)+(A2/po)VA -P"],(51)

P" = [X,Ci + p,, (C„ + Ciii )]: [l .< + /(poO) - 2a2 Р" + (A2 /po )V, Jq ]=

= X , [ l 3 tr C +/ ( p o O ) - 2 a ₂tr P "+ ( A 2, 'Po) V , ■ J q )+ 2 p , [ / 3 C +/ ( p o O ) - 2 a 2 P ' + ( A 2 /p o ) ( v , J q ) * ] ,

Из-за наличия временных и пространственных производных соотношения (50) – (52) обладают временной и пространственной нелокальностью.

Рациональная термодинамика сплошных сред (РТД)

Основы РТД были заложены в работах Колемана, Нолла, Трусделла, Тупина. В ней используется неравенство Клаузиуса – Дюгема pa“ =Pn + V-(j „/O)-pP/O> o,                    (53)

содержащее неравновесную энтропию n, и его модификация pa “ =pn + V-(j,,'O )-p₽/O > o,                      (54)

в которое так же, как в ТНПНТ, входит неравновесная температура O . Диссипативное неравенство (53) является интегральным обобщением неравенства Клаузиуса (17):

_& ext

Н> dQL^ ^ d fpn dV >-[^- n d S+ f^^ dV ^ — fpf| dV >-f^- n d S+ [^^ dV .

J O ^ext       dt V           J O V O dt V J O V O

При этом требование равновесности бесконечно близких состояний 1 и 2 снимается. Метод РТД очень популярен, потому что вывод определяющих соотношений осуществляется по единой, хорошо отработанной схеме. При фиксации одного из диссипативных неравенств (53), (54) отличия в результатах определяются, главным образом, списком назначаемых параметров состояния. Выбор параметров состояния определяется кругом физических явлений, для описания которых предназначается

Общие вопросы неравновесной термодинамики разрабатываемая модель среды. Для иллюстрации метода РТД можно ограничиться случаем изотропных материалов дифференциального типа сложности (1,0), состояние которых описывается набором параметров [3]

П = (о, F, 6, F, G).(55)

С помощью (2) диссипативное неравенство (53) можно привести к виду

Ро (f + п 6 )< Р:С - Jq - G/6,(56)

где f = e - 6f| - свободная энергия. Из принципа объективности поведения материалов можно установить, что величины f , п , J q , P зависят от (55) через параметры

П = (б, С, 6, С, G).(57)

С учётом данного факта из (56) получаем

( d f /56+р ) 6+ ( f /а с -р -¹ р ) :С + ( d f /а6>+ ( f /а С )-.С + ( a f /a G ) . G +Р о1 j q . g/ 6< 0. (58) Так как при заданных значениях (57) величины 6 , С , G могут быть произвольными, соотношение (58) распадается на три равенства:

af ^6 = о, af /аС = о, af /aG = о, которые означают, что f = f (6,С), как в термостатике, и на остаточное неравенство

( П - п ) 6 - Р о 1 P": С + Р о ¹ J q ■ G/6 <  0.                    (59)

Здесь P" определяется (23), п ( 6 , С ) - равновесная энтропия (энтропия Клаузиуса). В линейном приближении по 6 , С , G неравенству (59) удовлетворяют соотношения

П - п = ае(0,С)6 , P" = [1 v(6,С)С1 + рv(6,С)(СП + Сш)] :С, Jq = -Л(6,C)G, если материальные параметры о^ <о, 1 v > о, рv > о, A > о. Поэтому e = f + 6П = e'(6,С) + 6а6 (6,С)6, jq = -AV6,                  (бо)

где e'(6, С)=f (6, С)+6п(6, С) – внутренняя энергия при термодинамическом равновесии. Подставив (60) в (2), придём к уравнению теплопроводности в неподвижной среде р6а6 a 26/a t2 + р c a6/a t + р(а6 + 0aа0/a0)(a0/a t )2 = v . (av6)+рв, которое является уравнением параболического или эллиптического типа, так как а6 <о. Чтобы преодолеть тепловой парадокс при сохранении неравенства (53), нужно взять, например, набор параметров состояния [23]

П = ( 6 , С , G , J q )

и подчинить вектор теплового потока релаксационному уравнению J _q = H ( 6 , С , G , J _q ) , которое в линейном приближении подобно уравнению Максвелла – Каттанео – Лыкова: т ( 6 , C ) J q + J q =-A ( 6 , C ) G .

Не повторяя выкладок, отметим, что в этом случае внутренняя энергия e = e'(6,С)+а(6,C)Jq .

Принципиально иной результат получается при использовании неравенства (54), который впервые установили Грин и Линдсей [Ю] . В случае термоупругих материалов, состояние которых описывается набором параметров состояния

П = ( 6 , С , G , 6 ) ,                                   (б1)

из (54) получается диссипативное неравенство f + п6 -ро1Р : С + ро1 Jq - Vх6/6 < о,                   (б2)

в которое входит неравновесная свободная энергия f = e -6П . При равновесии 6=6> о.

С другой стороны, неравенства (54), (62) имеют смысл, если неравновесная

Общие вопросы неравновесной термодинамики температура не обращается в нуль при jq * 0, в ^ 0. Поэтому 0(ё, C, G, 0)> 0 . С учётом данных замечаний из (62) находим

( d f /5 C + П 50/5 C - p^{- 1} p ) : C + ( d f /5 G + n 50/5 G + р _о1 0 - 1 J q 50/50 ) - G + ( d f /50 + n 50/50 ) 0+ + р ₀ ¹ 0 - 1 50/d G -V X G ■ J q + р ₀ ¹ 0 - 1 50/5 C: V X C ■ J q + [ ( d f /50 + n 50/50 ) 0 + р _о1 0 - 1 50/50 J q • g] < 0 . Поскольку в каждом состоянии с параметрами (61) величины C , G , 0 , V _X G , V X C могут принимать произвольные значения, приходим к равенствам

P = Р ₀ ( f /5 C + П50/d e ) , J _q =-р ₀ [ 0/ ( её, d0 ) ] s f /5 G + n50 /sg) , n =- ( f ,'50 У( е ё /'50 ) , (63) 50/5 G , ( J q ) = -d0/5 G_; ( j „ ) , 50/5 C „( j , ) _k —50/d C , ( j „ )            (64)

и остаточному неравенству

( d f /50 + n 50/50 ) && + p ₀ 1 0^{- 1} 50/50 J _q • G <  0.                      (6 5)

Равенства (64) записаны в декартовой системе координат, они выводятся с учётом определений величин F, G, C . Первое равенство (64) означает, что диада 50/dG ® Jq является кососимметричным тензором второго ранга. Второе равенство указывает на то, что соответствующий тензор третьего ранга кососимметричен по последним двум индексам. Если в некотором состоянии с параметрами (61) вектор Jq не равен нулю, то тогда из требований (64) вытекает, что 50/dG = 0, d0/dC = 0 . В силу непрерывности эти условия должны выполняться и в случае J q = 0. Поэтому

0 = 0(0, 0)> 0 , 0 = 0(ё, 0 = 0)= 0 .(66)

Данный результат аналогичен соответствующему результату ТНПНТ. Благодаря (66) происходит упрощение соотношений (63):

P = р„5f/5C, Jq = -р„[0/(50,'50)]s/• /SG, n = -(df,S0)/(s0,/д0).(67)

Ограничившись проблемой бесконечной скорости распространения тепловых возмущений, рассмотрим поведение изотропных тел при отсутствии деформации. В квадратичном приближении можно записать следующие соотношения:

0 = a0 (o)+a, (o)0 + a2 (0)02, f = a0 (0)+ а, (0)0 + a2 (0)02 + b(o)G2.(68)

Отказываясь от простейшего случая a, = 0, a 2 = 0, на основе (66) получаем a 0 (0) = 0, a 2 (0)> 0, a2 (0)< 20a 2 (0).(69)

Подставив (68) в (67) и приняв во внимание (69), находим

Jq =-л(ё,0)g , Л = 2р0b(o)[o + a1 (o)0 + a2(o)02 ]/[a1 (ё) + 2a2 (o)0],(70)

n = -[a1 (o)+ 2 a 2 (0)0 ]/[a1 (0) + 2a 2 (0)0 ].(71)

Если в (65) положить 0 = 0, получим b ( o )/ a , ( ё ) > 0. Значит, в равновесных условиях коэффициент теплопроводности л ( ё , 0 = 0 ) > 0. Однако в неравновесных состояниях коэффициент теплопроводности (70) может принимать отрицательные значения. Поэтому в нестационарных процессах неравенство J _q ■ G <  0 может быть нарушено.

Выражениям (68), (71) отвечает следующее выражение для внутренней энергии:

e =. f + 0n = a 0 ( 0 ) + а , ( о ) ) + a 2 ( O ) 0 ² + b ( 0 ) G ² - a ^{l (0)+} 2 a ^{2 (l}°⁾⁰ [ a . ( 0 ) + a , ( O ) 0 + a 2 ( O ) 0 ² ] . (72) a 1 (0) + 2 a ₂ (0) 0

В линейном приближении по параметрам (0, G) выражение (72) имеет вид e = e'(О) + т0 (0)0, e' = а0 (о) - 0 а, (0)/a, (о), т0 = 20 [а, (o)a2 (о) - а2 (o)]/a, (О).    (73)

Точно так же для вектора теплового потока (70) находим

Общие вопросы неравновесной термодинамики

J q =-Л о ( e ) G , Л о = 2 p o O b ( e )/ a ( e ) .                   (74)

На основании (73), (74) из (2) получается уравнение теплопроводности to s2 e/st2 = Р01Л 0v2 e+p01 (ve)2 sл 0 /so - (se/st )2 st0 /so - c se/st+p, которое имеет гиперболический тип, если только To > 0.

Термодинамика сплошных сред с функцией рассеяния (ТДФР)

Другое направление в термодинамике сплошных сред, восходящее к Р. Клаузиусу, М. Планку, Т. де Донде и связанное с именами А.А. Ильюшина, Л.И. Седова, С.К. Годунова, А.А. Вакуленко, Б.Е. Победри, Г. Циглера и многих других отечественных и зарубежных учёных, основывается на уравнении баланса неравновесной энтропии pen = -V • jq + рв + pw, w > 0 .                        (75)

Величина w называется (массовой) функцией рассеяния [24], скоростью диссипации работы [25], мощностью некомпенсированной теплоты [4]. В последнем случае используется обозначение w = q', где q' - некомпенсированная теплота. Диссипативное неравенство (75) является дифференциальным обобщением неравенства Клаузиуса (17), относящимся к бесконечно малому индивидуальному объёму среды массы m , нjm > (qext m)/eext ^ n > qext /e ^ n > qext /e.                    (76)

Обычно требование равновесности бесконечно близких состояний 1 и 2 снимается. ТДФР широко применяется при моделировании пластических сред, поэтому требование ТНП на обратимость квазистатических процессов в ТДФР также снимается [ 4 ] .

Как правило, для вектора теплового потока принимается закон Фурье j _q =- Л •Ve [ 1 ] . В этом случае из условия w >  0 вытекает неотрицательность производства энтропии: оП¹ ' >  0. Следующим шагом в цепочке обобщений (76) является замена в (75) абсолютной температуры О неравновесной температурой О :

р w = pOn + V^ j q -Рв> 0.                           (77)

С помощью уравнения внутренней энергии (2) термодинамическое соотношение (77) можно представить в виде так называемого неравенства Клаузиуса - Планка [ 3, 26 ]

w = Оn- e + p^{- 1} T:D > 0, w = On- e + p ₀ ¹ P:C > 0.                  (78)

При термодинамическом равновесии О = О , n = n , где ц - равновесная энтропия (для вязкоупругих сред n совпадает с энтропией Клаузиуса n ( O , C ) ; для пластических сред равновесная энтропия зависит от большего числа параметров, в которые обычно входит та или иная мера пластической деформации, параметры упрочнения и т.п.).

Проиллюстрируем особенности ТДФР на примере пластической среды, состояние которой описывается набором параметров П = (О,C,х,О,C,G). Здесь х = (х1,X2,X3,—) — набор внутренних параметров состояния, описываемых эволюционным уравнением х = fx(n).                                         (79)

Так как величины n , e , P , w полагаются функциями П , из соотношения (78) имеем w ( n ) = О ( п ) П ( п ) - e ( n ) +p ₀ ¹ p ( n ) : C& = ( О Эц/so-s e / se ) o+ ( О Эц/s C -s e / s C +p ₀ ¹ p ) :CP +

+ ( О sn/s % - s e / s x ) * х + ( О sn/sO - se, sO )e> + ( О sn /s C& - s e / s C ) :C + ( О sn /s G - s e/ s g )^ G >  0 .

Поскольку функция рассеяния не зависит от О , C , G , то с учётом эволюционного уравнения (79) приходим к равенствам

Общие вопросы неравновесной термодинамики e an/аё - аe/ae = о, 0 an/aC - ae/aC = 0, e an/ас - ae/dG = 0      (80)

и остаточному неравенству w = (ean/ae - ae/ae)e + (ean/ас - аe/ac + p01P): C + (ean/ax - ae/ax)* x > 0. (81) Введём обозначения xer =-(edin/ae-аe/ae), p01Pr =-(ean/ас-ae/ac), xr = -(ean/ax-ae/ax), (82)

X ' r ^ - X ^r _e , P ^ir ^ P - P ^r , X i = - X X .                         (83)

Следуя [ 25 ] , величины (82) можно назвать обратимыми внутренними силами, а величины (83) — необратимыми внутренними силами. Умножим выражения (82) на произвольные приращения (вариации) 80 , 8 C , 5 X , а выражения (80) на 80 , 8 C , 8 G соответственно. Сложив полученные результаты, придём к уравнению

08n -8 e = - ( х0 80 + p ₀1 P ^r : 8 C + X r, * 8 x ) ,                      (84)

связывающему приращения энтропии и внутренней энергии с вызвавшими их произвольными (виртуальными) приращениями параметров состояния (при рассмотрении истинных приращений, получаемых соответствующими величинами за промежуток времени dt, надо заменить в (84) знак 8 знаком d). Из соотношений (81) -(83) вытекает выражение для функции рассеяния w = Xer0 + p01Pir :C + X* * x > 0,(85)

разложение тензора напряжений на обратимую и необратимую составляющие

P = pr + pir,(86)

а также характерные равенства

X0 + Xer = 0, x; + Xir = 0.(87)

Соотношения (84) – (87) лежат в основе общего формализма ТДФР.

Замечание. Когда понятие неравновесной температуры не привлекается, возможно упрощение термодинамических соотношений. Если в (84) вместо 0 подставить 0 и перейти к свободной энергии f = e - en , будем иметь

8 f = ( X ₆ ^r - n ) 8e + p 0 ^{- 1} P ^r : 8 C + X X * 8 x .                         (88)

Поэтому f = f ( e , C , x ) , т.е. свободная энергия зависит от меньшего числа параметров, чем энтропия и внутренняя энергия. В результате P ^r = P ^r ( 0 , C , x ) , X X = X X ( 0 , C , x ) .

8f = (X6r-n)зe + p01Tr : 8c + XX*8x, f = e-0п .(90)

В теории малых упругопластических деформаций тензор напряжений и функция рассеяния при активном нагружении имеют вид [ 24, 27 ]

T = [KtrE -Y(0-00 )]I + 2p[1 -to(£u )]8 , p0w = (2 3)oud[8uto(£u )]/dt > 0.

Здесь K, p, у - независящие от температуры модуль объёмного сжатия, модуль сдвига и коэффициент температурных напряжений, а„ = V(3/2)T: T , 8„ = 4(3/2)ё : 8(92)

• - интенсивности тензора напряжений и тензора деформации, ® ( 8 _u ) - функция пластичности Ильюшина, удовлетворяющая требованиям [ 27 ]

• ¹    >  ^{d [8} u ю ( ⁸ u )Р ^{d 8} u >Ю> ⁰ , ^d ® ( ⁸ u )/ ^{d 8} u >  ⁰ -

• Общие вопросы неравновесной термодинамики

Первичной для расчёта функции рассеяния является зависимость е„

u

J o ud ^в и

V 0

2 d

^-О и ⁴ м

J

Ро w =

Несущественная разница (в значениях коэффициентов) между (91) и аналогичным выражением для Роw из [27] связана с принятыми определениями (92).

Подставив выражения ви , oи , T в выражение (91) для w, получим w = Ро1 М1 -ю)d(вию)/dви ]~ : ~ > 0.

Сопоставив (93) со вторым выражением (89), находим

XLr = 0, T " = [2ц(1 - ю)d(е и ю)Ув и ]~.(94)

При этом список внутренних параметров χ пуст. Исходя из (94), (87), третьего соотношения (89) и первого уравнения (91), имеем

X 0 = о, Tr = [K trE - у(0 - 00 )]I + 2ц(1 - ю)[1 - d(s и ю)/ da и ] ~ .(95)

Следовательно, на основании (90) f = f ( 0 , e ) , n = n ( 0 , e ) . Данные зависимости можно определить, если известна функция пластичности Ильюшина ю ( в _и ) .

В [4] при моделировании пластических сред за основу берутся соотношения w = р01т: Ep > 0, E = Ee + Ep, f = f (о,Ee,Ep),(96)

которые выписаны в приближении малых деформаций. Здесь τ – некоторый тензор, характеризующий диссипацию энергии, εe и ε p – упругая и пластическая составляющие линейного тензора деформации ε . Переписав выражение для свободной энергии в виде f = f (o,e,Ep), приходим к выводу, что список внутренних параметров состояния состоит из тензора пластической деформации: х = ep . Сравнив первое выражение (96) с (89) и приняв во внимание (87), (90), получим

X 0r = 0, Tr = 0, X Г =Р01т, X 0 = 0, T = Tr, X Х=-Р01т ,(97)

5f = -р5О + Ро1T : 5e - Р-1т: 5ep, T = Р0 5f /dE, т = -Р0 5f /5ep .(98)

Чтобы в (96) удовлетворить условию w >  0 , достаточно принять

Ep = Х т , Х> 0.(99)

В (99) знак строгого неравенства отвечает режиму пластического деформирования, а знак равенства – режиму упругого деформирования. Смена режима деформирования определяется некоторым условием пластичности, например, условием Губера – Мизеса:

F ( t , e p , 0 , к ) ^о и -о ₅ ( 0 , e p , к ) = 0,                       (100)

где о ₅ - предел текучести на растяжение, к - некоторый параметр упрочнения.

Если материал пластически несжимаем (tr E ^p = 0), то тогда

T = o I + T , о = K ( o ) tr E - y ( 0 - 0 ₀ ) , E e = T /[2 ц ( о ) ] .

Поэтому ввиду второго уравнения (96) в области упругого деформирования ( о _и <  о ₅ )

будет выполняться уравнение состояния Дюамеля – Неймана

T = [ K ( 0 ) tr E - y ( 0 - 0 ₀ ) ] I + 2 ц ( 0 ) ( ~ - e p ) .

Отсюда на основании (98) находим f = Р01 J T: dE = f 0 (О) + Р01 0,5 K(o)(trE)2 -Y(o-00)trE + ц(0)tr(~ - Ep)2 , т = 2ц(0)(~ - ep )= T.                             (101)

Общие вопросы неравновесной термодинамики

Соотношение (101) совместно с уравнением (99) приводит к закону пластического течения, ассоциированному с условием пластичности (100): Ё p = Xd F /д Т .

Сравнение (97) с (94), (95) показывает, что термодинамическое содержание теории пластического течения и деформационной теории разное, даже для процессов простого нагружения, при которых обе теории одинаковы с механической точки зрения [ 28 ] .