Термодинамический анализ равновесных процессов в сложных природных системах

• 1.    Введение

• 2.    Методика исследования

  Использование недостаточно полной информации при определении термодинамических условий образования природной системы может повлиять на достоверность результатов исследования. При традиционном подходе в расчётах обычно учитывается только часть химических соединений, которые могут принимать участие в реакциях. Но неучтённые соединения могут оказать существенное влияние на давление и температуру. Поэтому выбор количества компонентов в исследуемой системе должен обеспечить возможность составления всех реакций, что позволит получить достоверный результат. В этой связи наиболее привлекательным нам представляется метод TWQ ( Berman , 1991). Данный метод оценивает равновесное состояние из сравнения поведения констант равновесия ( Кр как функция Р и Т ) химических реакций, возможных в данной системе, и позволяет осуществлять расчёт величин давления и температуры по химическому составу всех присутствующих фаз (соединений). Метод использует обширную внутренне согласованную базу термодинамических характеристик химических соединений. В основу расчёта положены следующие уравнения:

Термодинамическим исследованиям отводится важная роль при анализе процессов, сопровождаемых химическими и фазовыми превращениями в широком интервале температур и давлений. Для равновесных или локально равновесных процессов расчёт параметров состояния позволяет с относительно высокой точностью моделировать реальные условия и представлять информацию, которую обычно трудно получить экспериментальным путём. В связи с этим путём расчёта проводится предварительная оценка наличия сосуществующих в условиях равновесия химических соединений в реагирующей смеси. Действительно, исследованиям, например, синтеза новых химических соединений при высоких давлениях и температуре обычно предшествует детальный термодинамический и кинетический анализ путей решения поставленной задачи.

Принято считать, что "...состав и термодинамические свойства равновесных продуктов однозначно зависят от элементарного состава, температуры и давления" ( Зельдович , 1938). Это же соотношение является главным и при решении обратной задачи химического равновесия. Это позволяет широко использовать термодинамические методы исследования для решения некоторых геологических задач. Оценка температуры и давления среды (термобарометрический расчёт), при которых происходило образование минералов, является важной задачей для прогнозирования протекающих в природных условиях постмагматических (метаморфических) процессов. Для данной цели исследуют химический состав совместно присутствующих в природном образце минералов и осуществляют расчёт на основании констант равновесия химических реакций. Так, для определения зависимости константы равновесия от температуры при постоянном давлении обычно использовали следующее уравнение: d (ln Kp ) / dT = Δ H / RT ². Для случая изотермических условий зависимость константы равновесия от давления выглядит следующим образом: d (ln Kp ) / dP = Δ V / RT .

T = [ΔHo + ΔVo (P-1)] / (ΔSo - RlnKp),     P = (- RTlnKp - ΔHo + TΔSo) / ΔVo, где ΔHo, ΔSo и ΔVo - изменение энтальпии, энтропии и объёма соединений, участвующих в реакции.

Отсюда находятся константы равновесия химических реакций как функции температуры и давления. При равновесии в исследуемой системе расчётные кривые констант равновесия должны пересечься на Р-Т плоскости в одной точке. В данном случае равновесие среды определяется фазовым и химическим составами, а уравнения, определяющие Р , Т и составы равновесных фаз в точке пересечения, получаются из условия равенства химических потенциалов компонентов системы во всех фазах. Если по результатам расчёта исследуемая система является неравновесной, то на Р-Т плоскости за счёт смещения кривых констант равновесия образуется некоторая область, размеры которой пропорциональны степени отклонения системы от состояния равновесия. Возможности метода позволяют решать и обратную задачу, т.е. по известным значениям температуры и давления установить, существует ли равновесие в исследуемом объекте или системе. В данной работе проведена оценка возможностей метода TWQ на примере одного из природных объектов Кольского полуострова.

Основой для исследований явилось детальное петрографическое и микрозондовое изучение химического состава минеральных фаз. В процессе модельных исследований предусмотрено решить задачу по определению Р-Т параметров превращения исследуемого природного объекта во вторичные (метаморфические) минералы в присутствии летучих компонентов при равновесных условиях. Метаморфическая система, как сложная природная система, рассматривается как результат эволюционирования совокупности всевозможных взаимосвязанных процессов. В качестве примера для исследования мы использовали образец (Панская интрузия, Кольский полуостров), имеющий следующую минеральную ассоциацию: плагиоклаз, амфиболы, серпентины, хлорит, клиноцоизит. Химический состав некоторых минеральных фаз представлен в таблице.

	SiO 2     Al 2 O 3     FeO     MgO    CaO    Na 2 O    K 2 O
Амфибол 1 Амфибол 2 Клиноцоизит Плагиоклаз	53.40      5.36      11.00     15.61      12.51      0.74      0.18 52.85      6.45      10.86     15.01      11.95      0.90      0.20 40.37     24.72     10.26     0.15     22.76     0.27      0.00 55.58     28.30     0.00      0.00      10.38      5.74      0.00

Как видно из таблицы, исследуемая минеральная система представлена следующим элементарным составом: Si, Al, Fe, Ca, Mg, Na, K, H, O. В соответствии с петрографическим составом природного образца для расчёта в исследуемую систему на начальном этапе были включены следующие минералы: NaAlSi 3 O 8 (альбит), CaAl 2 Si 2 O 8 (анортит), Ca 2 Fe 5 Si 8 O 22 (OH) 2 (актинолит), Ca 2 Mg 5 Si 8 O 22 (OH) 2

(тремолит), Ca₂Al₃Si₃O₁₂(OH) (клиноцоизит), Ca₂FeAl₂Si₃O₁₂(OH) (эпидот), Fe₃O₄ (магнетит) и SiO₂ ( α -кварц). Термодинамические характеристики перечисленных соединений брались из совмещённой базы данных метода TWQ, в которую внесён справочный материал из ( Holland and Powell , 1990).

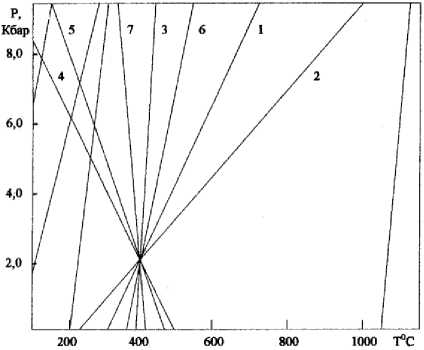
Рис. 1. Р - Т диаграмма химических реакций системы (подробности в тексте)

На начальном этапе исследования был рассмотрен вариант "сухой" (безводной) минеральной системы. Моделирование показало, что химическое взаимодействие между указанными компонентами отсутствует. При последовательном введении в указанную минеральную систему летучих компонентов (воды, водорода и кислорода) было отмечено протекание многочисленных химических реакций. Было установлено, что значительное усложнение химического состава системы приводит к её постепенному отходу от равновесного состояния. В связи с этим истинные Р - Т параметры в сильно усложнённой системе оценить оказалось невозможным. Для системы, в которой присутствуют все летучие компоненты, расчет показал наличие ряда химических реакций и отсутствие равновесия. Детальный анализ позволил установить, что отклонение системы от равновесных условий обусловлено реакциями, в которых принимал участие водород.

Термодинамическим расчётом системы при отсутствии водорода установлено, что остальные химические соединения могут находиться между собой в состоянии равновесия при Т = 404°С и Р = 2.18 Кбар (рис. 1). При этих параметрах существуют семь реакций (из одиннадцати), константы равновесия которых на Р - Т диаграмме пересеклись в одной точке (их номера показаны на кривых рис. 1):

26 CaAl 2 Si 2 O 8 + 10 Ca 2 FeAl 2 Si 3 O 12 (OH) + Ca 2 Fe 5 Si 8 O 22 (OH) 2 + 6 Н 2 О =

= 24 Ca2Al3Si3O12(OH) + 5 Fe3O4 + 18 SiO2

24 Ca2Al3Si3O12(OH) + 4 Fe3O4 + 12 SiO2 + О2 = 24 CaAl2Si2O8+ 12 Ca2FeAl2Si3O12(OH) + 6 Н2О(2)

2 CaAl2Si2O8+ Ca2Fe5Si8O22(OH)2 + О2= 2 Ca2FeAl2Si3O12(OH) + Fe3O4+ 6 SiO2

2 Ca 2 Fe 5 Si 8 O 22 (OH) 2 + 24 Ca 2 Al 3 Si 3 O 12 (OH) + 2 Fe 3 O 4 + 3 О 2 =

= 20 CaAl2Si2O8 + 16 Ca2FeAl2Si3O12(OH) + 6 Н2О(4)

12 Ca 2 Fe 5 Si 8 O 22 (OH) 2 + 24 Ca 2 Al 3 Si 3 O 12 (OH) + 13 О 2 =

= 36 Ca2FeAl2Si3O12(OH) + 8 Fe3O4+ 60 SiO2 + 6 Н2О(5)

36 CaAl 2 Si 2 O 8 + 6 Ca 2 Fe 5 Si 8 O 22 (OH) 2 + 6 Н 2 О + 5 О 2 =

= 24 Ca2Al3Si3O12(OH) + 10 Fe3O4+ 48 SiO2

24 Ca 2 Al 3 Si 3 O 12 (OH) + 4 Ca 2 Fe 5 Si 8 O 22 (OH) 2 + 5 О 2 =

= 16 CaAl2Si2O8+ 20 Ca2FeAl2Si3O12(OH) + 12 SiO2 + 6 Н2О(7)

В химических реакциях (1-7) отсутствуют соединения, содержащие натрий и магний. Это явилось результатом недостаточно корректного отбора в исследуемую систему химических соединений, которые могли бы принять участие в реакциях. Вместе с тем следует отметить, что установленное химическими реакциями (1-7) равновесие можно считать действительным для системы с указанным составом минералов, но при отсутствии в ней альбита и тремолита. Поэтому была предпринята попытка ввести химические соединения, содержащие натрий и магний. В исследуемую систему вводились отдельно и попарно Na- и Mg-содержащие минералы: паргасит, магнезиорибекит, эденит, глаукофан. Было установлено, что всякое усложнение системы также способствует выводу её из состояния равновесия. Равновесное состояние в системе, содержащей минералы всех указанных элементов, было установлено после замены актинолита (активно участвующего в реакциях 1, 3-7) на паргасит [NaCa 2 Mg 4 Al 3 Si 6 O 22 (OH) 2 ]. Расчёты показали, что равновесное состояние в откорректированной системе определяется следующими химическими реакциями:

4 Ca 2 Mg 5 Si 8 O 22 (OH) 2 + 14 CaAl 2 Si 2 O 8 + 5 NaAlSi 3 O 8 + 4 Н 2 О =

= 6 Ca2Al3Si3O12(OH) + 5 NaCa2Mg4Al3Si6O22(OH)2 + 27 SiO2

24 Ca 2 Al 3 Si 3 O 12 (OH) + 4 Fe 3 O 4 + 12 SiO 2 + O 2 =

= 12 Ca2FeAl2Si3O12(OH) + 24 CaAl2Si2O8+ 6 Н2О(9)

12 Ca 2 Mg 5 Si 8 O 22 (OH) 2 + 30 Ca 2 Al 3 Si 3 O 12 (OH) + 15 NaAlSi 3 O 8 + 8 Fe 3 O 4 +2 О 2 =

= 6 CaAl2Si2O8 +24 Ca2FeAl2Si3O12(OH) + 15 NaCa2Mg4Al3Si6O22(OH)2 + 57 SiO2

6 Ca 2 Mg 5 Si 8 O 22 (OH) 2 + 192 Ca 2 Al 3 Si 3 O 12 (OH) + 20 NaAlSi 3 O 8 + 36 Fe 3 O 4 + 9 О 2 =

= 160 CaAl2Si2O8+ 108 Ca2FeAl2Si3O12(OH) + 20 NaCa2Mg4Al3Si6O22(OH)2 + 38 Н2О(11)

48 Ca 2 Mg 5 Si 8 O 22 (OH) 2 + 96 Ca 2 Al 3 Si 3 O 12 (OH) + 60 NaAlSi 3 O 8 + 28 Fe 3 O 4 + 6 Н 2 О + 7 О 2 =

= 84 Ca2FeAl2Si3O12(OH) + 60 NaCa2Mg4Al3Si6O22(OH)2 +240 SiO2

Ca 2 Mg 5 Si 8 O 22 (OH) 2 + 32 CaAl 2 Si 2 O 8 + 20 NaAlSi 3 O 8 + 4 Fe 3 O 4 + 10 Н 2 О + О 2 =

= 12 Ca2FeAl2Si3O12(OH) + 20 NaCa2Mg4Al3Si6O22(OH)2 + 96 SiO2

В связи с тем, что паргасит является более высокотемпературным минералом по сравнению с исключёнными соединениями, его появление в системе вызвало смещение ранее установленных параметров в область более высокой температуры.

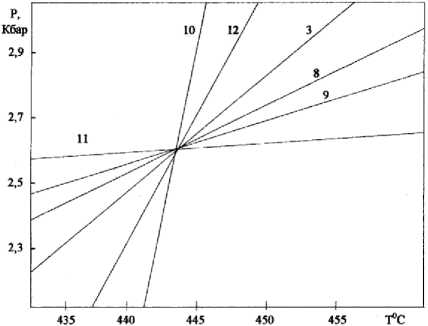
Рис. 2. Оценка Р - Т параметров природного образца согласно установленному равновесию в системе

Кривые констант равновесия химических реакций (8-13) на Р - Т диаграмме, как следует из рис. 2, пересеклись в одной точке при Т = 443°С и Р = 2.62 кбар.

4. Выводы

По данным фазового и химического состава исследуемого объекта теоретическими расчётами установлены температура и давление среды образования минералов в природных условиях. Показаны возможности термодинамического расчёта параметров равновесия по результатам химического анализа и химических реакций, протекающих в исследуемой системе. Отмечается, что определение величин давления и температуры возможно при условии детальных микрозондовых и петрографических анализов, а также при корректной постановке задачи.