Термодинамический анализ реакции водяного газа

Водяной газ – четырехкомпонентная смесь Н2 – Н2О–СО–СО2 – является основой газовых атмосфер во многих металлургических технологиях. Параметры равновесия реакции водяного газа

H 2 + CO 2 = H 2 O + CO достаточно просто рассчитываются с использованием константы равновесия:

p H 2 O p CO   (% H 2 O)(% CO)

K n (1) = K (1) =--------=---------------= p c    pH2 pCO2   (%H2)(%CO2)

понентов водяного газа, удовлетворяющих соотношениям (4). Получить водяной газ нужного состава можно нагреванием до заданной температуры смеси «Н₂, a ₀ моль – СО₂, d ₀ моль» при исходных концентрациях x _co = x Н₂о = 0; или смеси «Н₂О, b ₀ моль – СО, c ₀ моль» при исходных концентрациях x Н₂ = X co₂ = 0. Подтвердим это чис-

x H₂O x CO x H₂ x CO₂

A G (1) e RT

ленными расчетами.

Пусть смесь водорода и углекислого газа нагревается до заданной температуры в реакторе любого объема при любом давлении:

Стандартное изменение энергии Гиббса (Дж) для реакции водяного газа с учетом температурных зависимостей тепловых эффектов реакций, изменения энтропии и теплоемкостей газов [1, 2]

A _rG_T (1) = 47 584 - 1,263 • 10 ^{- 3} T ² - ^3,963 0—

Н 2 + СО 2 = Н 2 О + СО

Исходный состав a ₀ d ₀      –    –

Равновесный состав    a ₀ – x d ₀ – x   x    x

Здесь a 0 и d 0 – числа молей Н 2 и СО 2 в исходной смеси. Если для простоты расчетов положить a 0 + d 0 = 1 моль, тогда a 0 – x , d 0 – x , x и x – моляр-

- 132,956 T + 13,011 T In T . (2)

Довольно часто в практических расчетах используют приближенные уравнения. Например, для реакции водяного газа в справочниках и научной литературе рекомендуется пользоваться приближенным линейным уравнением [2]

A _rG T (1) = 36 580 - 33,465 T . (3) Результаты расчетов по уравнениям (2) и (3) хорошо совпадают при температурах ниже 1200 К. Поэтому при расчетах процессов твердофазного восстановления, например оксидов железа (особенно в присутствии углерода), допустимо использование приближенного уравнения (3).

Если переписать константу равновесия реакции водяного газа в таком виде:

K 1 = xco/xco^, xco = K JH., (4) xH2 xH2O xCO2 xH2O то количественную информацию о равновесии реакции при разных температурах можно представить номограммой, на которой изотермы – прямые линии, угловой коэффициент которых равен константе равновесия (рис. 1). График на рис. 1 иллюстрирует важную особенность равновесия реакции водяного газа – для любой температуры возможно множество концентраций ком-

ные доли компонентов равновесного водяного газа. Получаем для константы равновесия

K 1 =

.

⁽ a 0 ^- x ⁾⁽ d 0 ^- x )

Решение этого квадратного уравнения (при

K 1 * 1) представляется уравнением

^x CO = ^x Н₂О =

0,5 K ₁

1 - K

±

^K 1 a 0 d 0 +1 0,^{5 K} 1 |    (6)

1 - K 1   ( 1 - K 1 ) . ¹

Из результатов вычислений по этому уравнению следует, что физический смысл имеет один из двух корней, причем для K 1 <  1 перед квадратным корнем следует ставить знак «+», а для K 1 >  1 - знак «-». При K 1 = 1 (1093 К) из уравнения (5) получается a ₀ d ₀

x a ₀ + d 0.

Результаты расчетов составов равновесного водяного газа для трех температур представлены в табл. 1–3 и точками для разных соотношений a ₀ / d ₀ на соответствующих изотермах номограммы на рис. 1. Для примера на рис. 2 представлены результаты расчетов для температуры 1093 К. Рис. 3 отмечает еще одну важную особенность – сумма концентраций газов-восстановителей и сумма концентраций газов-окислителей зависят только от состава нагреваемой смеси, но не зависят от температуры.

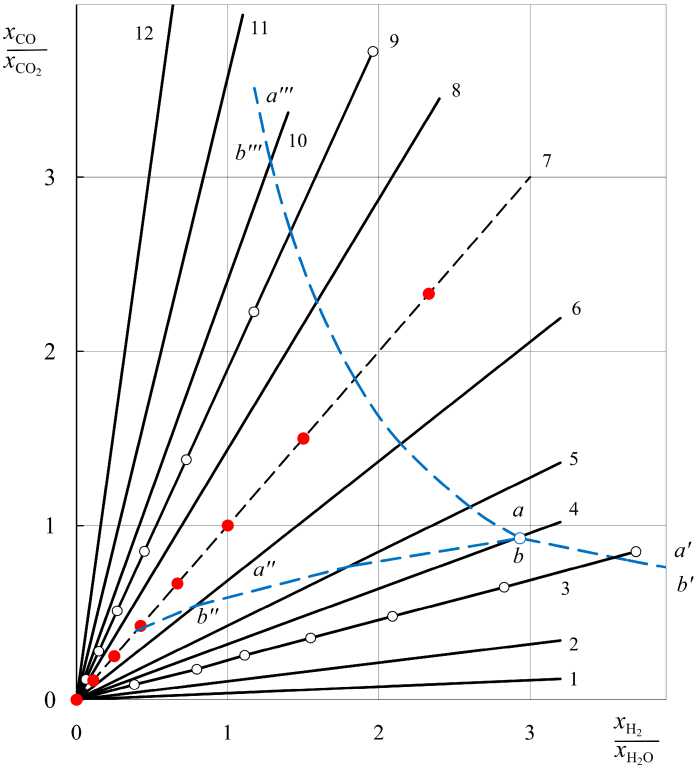
Рис. 1. Соотношения между x _CO/ x _CO₂ и x H₂ / x H₂O равновесного водяного газа: 1 – 600, 2 – 700, 3 – 800, 4 – 850, 5 – 900, 6 – 1000, 7 – 1093, 8 – 1200, 9 – 1300, 10 - 1400, 11 - 1600, 12 - 2000 К; линии aa’ ( bb’) , aa” ( bb^fr) , aa^m ( bb^{n r} ) - равновесия водяного газа со смесями Fe 3 O 4 -Fe, Fe 3 O 4 -FeO, FeO-Fe; точка a ( b ) - нонвари-антное равновесие Fe 3 O 4 –FeO–Fe–H 2 –H 2 O–CO–CO 2

Таблица 1

Возможные параметры равновесия реакции водяного газа при 800 К

a o d o	1 0	0,9 0,1	0,8 0,2	0,7 0,3	0,6 0,4	0,5 0,5	0,4 0,6	0,3 0,7	0,2 0,8	0,1 0,9	0 1
x СО = x H2O	0	0,0724	0,1153	0,1420	0,1570	0,1618	0,1570	0,1420	0,1153	0,0724	0
x H2	1	0,8276	0,6848	0,5580	0,4430	0,3382	0,2430	0,1580	0,0848	0,0276	0
x CO2	0	0,0276	0,0848	0,1580	0,2430	0,3382	0,4430	0,5580	0,6848	0,8276	1
x H2 x H2O	0	0,382	0,7354	1,1122	1,5483	2,09	2,8224	3,928	5,9414	11,438	—
x CO x CO2	0	0,08074	0,1683	0,2545	0,3543	0,4784	0,6459	0,8991	1,3599	2,618	—
lg( p O2, атм)	—	–28,60	–28,03	–27,67	–27,38	–27,12	–26,86	–26,58	–26,22	–25,64	—

Таблица 2

Возможные параметры равновесия реакции водяного газа при 1093 К

a o d o	1 0	0,9 0,1	0,8 0,2	0,7 0,3	0,6 0,4	0,5 0,5	0,4 0,6	0,3 0,7	0,2 0,8	0,1 0,9	0 1
x СО = x H2O	0	0,09	0,16	0,21	0,24	0,25	0,24	0,21	0,16	0,09	0
x H 2	1	0,81	0,64	0,49	0,36	0,25	0,16	0,09	0,04	0,01	0
x CO2	0	0,01	0,04	0,09	0,16	0,25	0,36	0,49	0,64	0,81	1
x H2 / x H2O	0	0,111	0,25	0,429	0,667	1	1,5	2,33	5,674	9	—
x CO / x CO2	0	0,111	0,25	0,429	0,667	1	1,5	2,33	5,674	9	—
lg( p O2, атм)	—	–19,78	–19,07	–18,60	–18,22	–17,87	–17,52	–17,13	–16,66	–15,96	—

Таблица 3

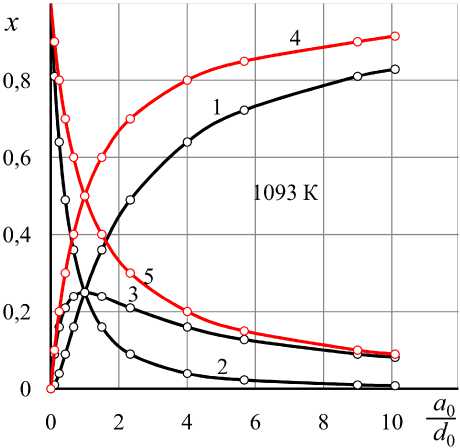
Рис. 2. Равновесные параметры водяного газа, полученном нагреванием исходной смеси «Н 2 , a ₀ моль + + СО 2 , d ₀ моль» до 1093 К: 1 – x _H ; 2 – x _CO ; 3 – x _CO ,

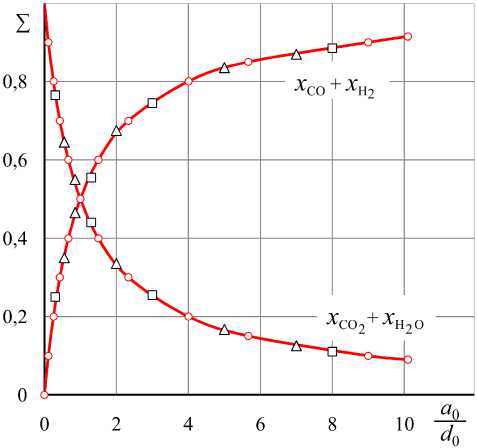
Рис. 3. Суммы концентраций восстановителей и окислителей в равновесном водяном газе, нагревание до 800 (∆), 1093 (○) и 1500 К (□)

Возможные параметры равновесия реакции водяного газа при 1300 К

ao do 1 0 0,9 0,1 0,8 0,2 0,7 0,3 0,6 0,4 0,5 0,5 0,4 0,6 0,3 0,7 0,2 0,8 0,1 0,9 0 1 xСО = xH2O 0 0,0942 0,1744 0,2365 0,2761 0,2897 0,2761 0,2365 0,1744 0,0942 0 xH2 1 0,8058 0,6256 0,4636 0,3240 0,2103 0,1240 0,0636 0,0256 0,0058 0 xCO2 0 0,0058 0,0256 0,0636 0,1240 0,2103 0,3240 0,4636 0,6256 0,8058 1 xH2 / xH2O 0 0,1169 0,2788 0,5101 0,8521 1,3776 2,2271 3,7207 6,808 — — xCO / xCO2 0 0,0616 0,1469 0,2688 0,4490 0,7259 1,1735 1,9605 3,5926 — — lg(pO2, атм) — –15,99 –15,23 –14,71 –14,26 –13,84 –13,43 –12,98 –12,46 –11,70 — xH2O ; 4 – (xH2 + xCO) ; 5 – ( xH2O + xCO2 )

Пунктирными линиями aa' (bb'), aa'' (bb''), aa''' (bb''') на номограмме (см. рис. 1) показаны хорошо известные «вилки», определяющие параметры равновесия газовых смесей CO–CO2 и H2 –H2O со смесями твердых фаз Fe3O4 –Fe, Fe3O4 –FeO и FeO – Fe. Точка пересечения линий a (b) ха- рактеризует параметры нонвариантных равновесий Fe3O4 –FeO–Fe–H2 –H2O и Fe3O4– FeO–Fe– CO–CO2.

В металлургической литературе принято количественно оценивать окислительно-восстановительные свойства газовой фазы величиной кислородного потенциала πО = RT ln pO . Для любой сколь угодно сложной газовой смеси, если в ней присутствуют СО2 и СО (или Н2О и Н2) и известны их концентрации, кислородный потенциал может быть вычислен при общем давлении 1 атм по уравнениям:

П О = -565 3 90 +

+

x

175,17 + 16,628ln-CO 2 x _CO

T , Дж

П О = -492 230 +

+

108,24 + 16,628ln ^ H 2 °

T , Дж

x H₂

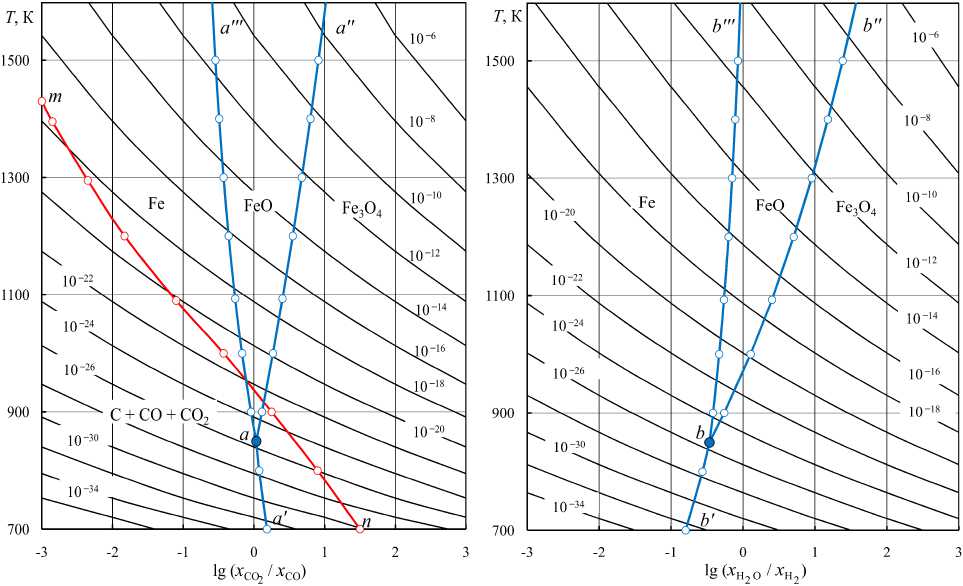
дяного газа при 1 атм: область ниже линии mn – термодинамическая неустойчивость CO (метастабильные состояния); линии aa' , aa'' и aa''' – равновесие газовой смеси CO–CO 2 с твердыми Fe 3 O 4 – Fe, Fe 3 O 4 – FeO и FeO–Fe; точка a – нонвариантная система Fe 3 O 4 – FeO–Fe– CO–CO 2

Рис. 5. Номограмма « lg( x _{H O} x _H ) - p _O - T » для водяного газа при 1 атм: линии bb' , bb'' и bb''' – равновесие газовой смеси H 2 – H 2 O с твердыми Fe 3 O 4 – Fe, Fe 3 O 4 – FeO и FeO–Fe; точка b – нонвариантная система Fe 3 O 4 –FeO–Fe–H 2 –H 2 O

Рис. 4. Номограмма « lg( x _CO x _CO) - p _O - T » для во

Эти уравнения основываются на термодинамических характеристиках реакций диссоциации диоксида углерода или паров воды при давлении 1 атм. Результаты расчетов величин lg( p _O , атм) водяного газа, получающегося нагреванием смесей Н₂ + СО₂, приведены в табл. 1–3. Для приблизительной оценки величины парциального давления кислорода можно воспользоваться номограммами [3], рис. 4 и 5. На номограммах представлены изобары кислорода и, для примера, равновесные параметры реакций восстановления оксидов Fe₃O₄ и FeO водородом и монооксидом углерода. На рис. 4 линия mn характеризует равновесие реакции C + CO₂ = 2CO. Параметры ниже этой линии характеризуют метастабильные состояния – выделения сажистого углерода.

Результаты расчетов (см. табл. 1–3) кроме обычных графиков (см. рис. 2 и 3) можно представить трехмерной диаграммой (рис. 6). Политерми-ческая поверхность на этой диаграмме определяет возможные сочетания концентраций Н₂ и СО в водяном газе, полученном нагреванием смесей «Н₂, a ₀ моль+СО₂, d ₀ моль». Образующими поверхности являются изотермические линии, которые представляются проекциями 1, 2 и 3 на плоскость x _H – x _СО (рис. 7). Эти проекции определяют

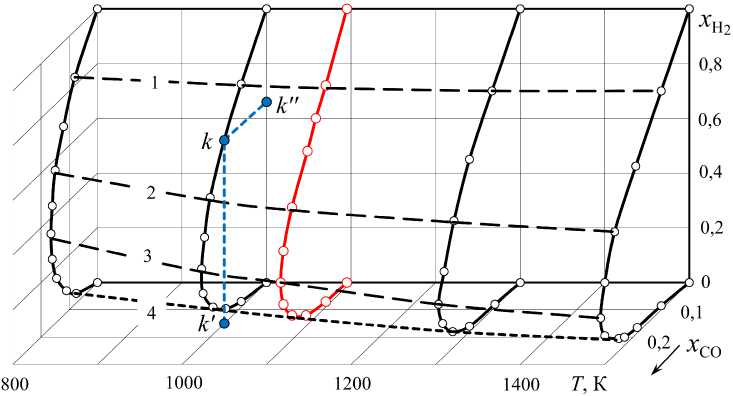
Рис. 6. Пространственная диаграмма, определяющая возможные соотношения между концентрациями H 2 и CO в равновесном водяном газе: изотермы 800, 1000, 1093, 1300 и 1500 К; исходные смеси (Н 2 , a ₀ моль + СО 2 , d ₀ моль): линия 1 – ^{a 0} = ^0,9 , 2 – ^0,7 , d ₀    0,1       0,3

3 – _{0 5} ; точка k : x _CO = 0,1498 ( k' ), x _H

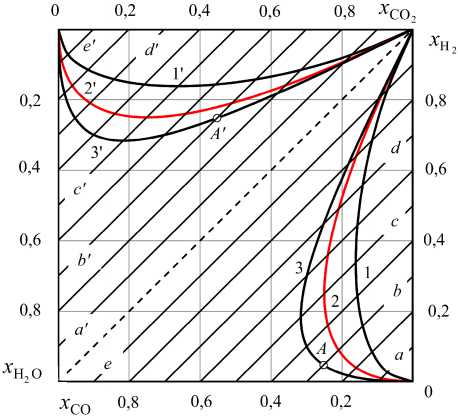
Рис. 7. Номограмма равновесных параметров водяного газа, полученного нагреванием смеси «Н 2 , a ₀ моль + + СО 2 , d ₀ моль»: 1, 2 и 3 – концентрации Н 2 и СО при 800, 1093 и 1500 К, 1 ′ , 2 ′ и 3' – концентрации Н 2 О и СО 2 при 800, 1093 и 1500 K; линии a , b , c , d и e : ^{a 0} = ^0,1 , d ₀    0,9

0,3 0,5 0,7    0,9

0,7 , 0,5 , 0,3 и 0,1

равновесные концентрации только Н₂ и СО. Равновесные концентрации Н₂О и СО₂ определяются на рис. 7 линиями 1 ′ , 2 ′ и 3 ′ . Соотношения равновесных концентрации Н₂О и СО₂ тоже могут быть представлены политермической поверхностью на пространственной диаграмме (чтобы не загромождать рисунок, эта поверхность на рис. 6 не показана, но ее положение можно представить по виду рис. 7).

= 0,6502 ( k'' ) – частный случай 1000 К,

a 0 ₌ 0,8

d ₀    0,2

Как следует из рис. 7, равновесный водяной газ кроме многообразия возможных концентраций компонентов характеризуется еще одной особенностью – зеркальной симметрией соотношений концентраций газов-восстановителей и концентраций газов-окислителей. Кроме того, политермиче-ские линии, соединяющие точки равновесных концентраций Н₂ (или СО) и Н₂О (или СО₂) газа, полученного нагреванием до разных температур исходных смесей Н₂ –СО₂ разных составов, оказываются прямыми. Например, в нижнем правом концентрационном треугольнике (см. рис. 7) точки пересечения с изотермами 1, 2 и 3 политермиче-ских линий b и d (концентрация водорода в исходной смеси 0,3 и 0,7, соответственно) определяют равновесные концентрации x _H и x _СО. В верхнем левом концентрационном треугольнике (см. рис. 7) проведены политермические прямые линии b ′ и d ′ . Точки пересечения этих линий с изотермическими кривыми 1 ′ , 2 ′ и 3 ′ определяют другие две равновесные концентрации: x _{H O} и x _CO . Каждая из линий a … e и a ′ … e ′ параллельна гипотенузе и пересекает оси координат в точках, характеризующих состав исходной смеси. Таким образом, равновесные параметры газа определяются номограммой, на которой можно провести диагональные линии для любых соотношений величин a ₀ и d ₀ в нагреваемых смесях Н₂ + СО₂.

Водяной газ можно получить нагреванием смесей «Н2О, b0 –СО, c0». Результаты расчетов равновесия реакции Н2О + СО = Н2+ СО2 представлены на рис. 8. И в этом случае получаются зеркально симметричные кривые, определяющие составы равновесного водяного газа. Разные поло- жения изотерм 800, 1093 и 1500 К на рис. 7 и 8 объясняются разными знаками тепловых эффектов:

– реакция Н2 + СО2 = Н2О + СО эндотермическая (рис. 7),

– реакция Н2О + СО = Н2 + СО2 экзотермическая (рис. 8).

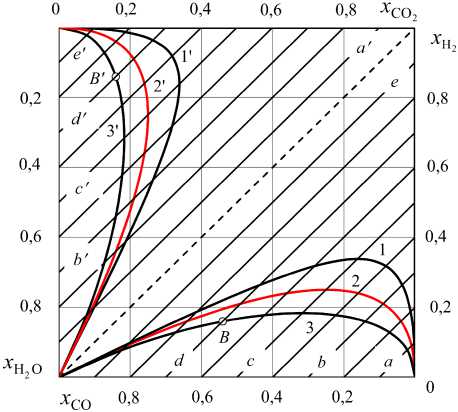
Рис. 8. Номограмма равновесных параметров водяного газа, полученного нагреванием смеси «H 2 O, b ₀ моль – CO, c ₀ моль»: линии 1, 2 и 3 – концентрации Н 2 и СО при 800, 1093 и 1500 К, линии 1 ′ , 2 ′ и 3' – концентрации Н 2 О и СО 2 при 800, 1093 и 1500 К; линии a , b , c , d и e : c     0,1  0,3  0,5  0,7    0,9

0=       ,        ,        , и b^   0,9  0,7  0,5  0,3    0,1

Приведем примеры использования номограмм для определения составов равновесного водяного газа при разных способах его получения.

• 1.    Состав равновесного водяного газа, получающегося при нагревании смеси (Н₂, 0,3 моль + +СО₂, 0,7 моль) до 1500 К определяется координатами точек пересечения линий b и b ′ с изотермами 3 и 3 ′ . Получаем x _H2 = 0,0477, x СО = 0,2523 (точка A , рис. 7); x _{H O} = 0,2523, x _CO = 0,4477 (точка A ′ , рис. 7).

• 2.    Состав равновесного водяного газа, получающегося при нагревании смеси «Н₂О, 0,3 моль –

  СО, 0,7 моль» до 1500 К определяется координатами точек пересечения линий d и d ′ с изотермами 3 и 3 ′ . Получаем x _H2 = 0,1596, x СО = 0,5404 (точка B , рис. 8); x _H2O = 0,1404, x CO₂ = 0,1596 (точка B ′ , рис. 8).

Выводы

• 1.    Равновесие водяного газа реализуется при бесконечном множестве возможных концентраций компонентов. Это согласуется с правилом фаз Гиббса: число степеней свободы системы H 2 – H 2 O–CO–CO 2

• 2.    Частные значения концентраций реализуются нагреванием до заданной температуры различных по составу смесей H₂ –CO₂ или H₂O–CO.

• 3.    Равновесные параметры водяного газа можно с достаточной точностью определять по номограммам. По этим же номограммам можно оценивать параметры исходных систем «оксид–H₂–CO₂» или «оксид – H₂O – CO». При нагревании этих систем до заданной температуры будет происходить восстановление оксида. Номограммы могут использовать студенты для самоконтроля правильности расчетов, или преподаватели для контроля результатов работы студента.

с = к + 2 – ф = 3 + 2 – 1 = 4.

В случае Р и Т = const число степеней свободы с = к – ф = 3 – 1 = 2, то есть равновесные характеристики системы можно определить, если задать какие-либо два параметра исходной системы.