Термодинамика системы "газовая турбина - эжектор - охладитель наддувочного воздуха" в дизеле с наддувом
Автор: Лазарев Е.А., Салов А.Ю., Лазарев В.Е.
Рубрика: Расчет и конструирование
Статья в выпуске: 3 т.24, 2024 года.
Бесплатный доступ
С позиций термодинамического подхода рассмотрены структурные и функциональные особенности элементов системы эжекционного охлаждения воздуха на выходе из компрессора в дизеле с газотурбинным наддувом. Выделены основные элементы системы: газовая турбина, эжекционное устройство (эжектор), охладитель воздуха после компрессора (наддувочного воздуха). Описаны физические процессы и их связи в элементах системы. Определены термодинамические параметры состояния, энергия газовоздушных потоков и их изменения в газовой турбине, эжекторе, установленном за турбиной турбокомпрессора на выпуске, и охладителе воздуха после компрессора. Рассмотрены связи между располагаемой и действительной работами, совершаемые отработавшими газами на выходе из цилиндра дизеля с газотурбинным наддувом. Приведены p,v- и i,s-диаграммы состояния газовоздушных потоков в элементах системы эжекционного охлаждения воздуха на выходе из компрессора. Рассмотренные особенности определения энергии и термодинамических параметров состояния отработавших газов в турбине турбокомпрессора, эжекционном устройстве и охладителе воздуха на выходе из компрессора использованы для оценки эффективности их совместной работы. Описаны способы повышения плотности наддувочного воздуха с выделением способа, использующего эжектор для реализации низкопотенциальной энергии отработавших газов дизеля. С использованием программного комплекс Solid Works определены скорости и температуры газовоздушных потоков в элементах эжекционного устройства (сопле, смесительной камере и диффузоре). Определен коэффициент эжекции эжекционного устройства как функция термодинамических параметров газовоздушных потоков. Отмечается целесообразность принятия компромиссных решений, при которых система эжекционного охлаждения может обеспечить максимальную плотность наддувочного воздуха при минимальных затратах энергии на циркуляцию охлаждающего воздуха через матрицу охладителя.
Компрессор, турбина, охладитель наддувочного воздуха, эжектор и его элементы, термодинамические параметры и энергия газовоздушных потоков, расходы газа и охлаждающего воздуха, коэффициент эжекции
Короткий адрес: https://sciup.org/147246014
IDR: 147246014 | УДК: 621.436 | DOI: 10.14529/engin240301
Текст научной статьи Термодинамика системы "газовая турбина - эжектор - охладитель наддувочного воздуха" в дизеле с наддувом
Улучшение технико-экономических и экологических показателей дизелей с газотурбинным наддувом достигается применением в качестве агрегата наддува наряду с турбокомпрессором промежуточного охладителя наддувочного воздуха (ОНВ). Охлаждение наддувочного воздуха (НВ) в ОНВ используют с целью дополнительного увеличения плотности и массового расхода свежего заряда для повышения мощности дизеля. Снижение температуры воздуха после компрессора осуществляется применением в качестве охлаждающих агентов: атмосферного воздуха, жидкости системы охлаждения дизеля, автономной системы жидкостного охлаждения [1, 2]. Охлаждение наддувочного воздуха атмосферным воздухом имеет ряд особенностей выбора источника циркуляции атмосферного охлаждающего воздуха (ОВ), в частности применение эжектора, рабочим потоком в котором являются отработавшие газы (ОГ) дизеля.
Для установления функциональных и структурных параметров, а также режимов работы системы эжекционного охлаждения целесообразно использовать термодинамический подход, который недостаточно изучен и требует отдельного рассмотрения элементов системы: газовой турбины, эжектора и охладителя наддувочного воздуха с описанием физических процессов, их связи и определением термодинамических параметров состояния, энергии газовоздушных потоков и их изменения [2, 3].
Необходимо рассмотрение особенностей связей между располагаемой и действительной работами при использовании низкопотенциальной энергии отработавших газов на выходе из цилиндра на основе анализа p , v- и i , s- диаграмм состояния газовоздушных потоков в элементах системы эжекционного охлаждения.
Для оценки эффективности совместной работы элементов эжектора требуется определение скоростей и температур потоков в сопловом устройстве, смесительной камере, диффузоре и коэффициента эжекции как функции термодинамических параметров газовоздушных потоков [4].
Материалы и методы
Термодинамический подход к определению энергетических характеристик элементов системы «газовая турбина - эжектор - охладитель наддувочного воздуха» лежит в основе оптимизации функциональных и геометрических параметров эжектора. Анализ энергетических процессов в газовой турбине, эжекторе и охладителе наддувочного воздуха позволяет оценить целесообразность принятия компромиссных решений, при которых система эжекционного охлаждения может обес- печить максимальную плотность наддувочного воздуха при минимальных затратах энергии на циркуляцию охлаждающего воздуха через матрицу охладителя. Для анализа рассмотрим структурную схему эжекционной системы охлаждения НВ (рис. 1) [4].
Рис. 1. Структурная схема эжекционной системы охлаждения НВ и параметры газовоздушных потоков в сечениях ее элементов: 1 – дизель, 2 – ОНВ, 3 – устройство измерения расхода воздуха, 4 – компрессор, 5 – турбина, 6 – трубопровод ОГ, 7 – трубопровод ОВ, 8 – эжектор
Fig. 1. Block diagram of the HB ejection cooling system and parameters of gas-air flows in the sections of its elements: 1 – diesel, 2 – ONV, 3 – air flow measurement device, 4 – compressor, 5 – turbine, 6 – exhaust gas pipeline, 7 – OV pipeline, 8 – ejector
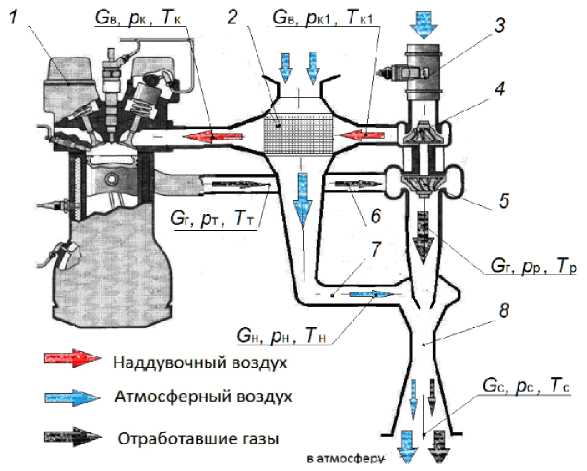
Атмосферный воздух через устройство измерения расхода 3 поступает во входное устройство компрессора 4 турбокомпрессора. Далее сжатый воздух после компрессора 4 под определенными давлением и температурой направляется в матрицу 2 охладителя наддувочного воздуха, где происходит теплообмен между НВ после компрессора и охлаждающим воздухом из атмосферы, и далее в цилиндры дизеля 1 [4].
Выделим и рассмотрим в структурной схеме эжекционного охлаждения систему в составе: газовая турбина 5, эжектор 8 и охладитель наддувочного воздуха 2, как термодинамическую систему с источником теплоты в виде отработавших газов дизеля 1 [5]. Отработавшие газы из цилиндров дизеля через трубопровод 6 поступают на турбину 5 турбокомпрессора, в которой срабатывается часть энергии ОГ для привода компрессора 4. После турбины ОГ через трубопровод 7 поступают в эжектор 8, где, расширяясь в сопле, передают оставшуюся часть кинетической энергии охлаждающему воздуху, увлекая и осуществляя его циркуляцию через ОНВ. После восприятия теплоты наддувочного воздуха охлаждающий воздух из атмосферы, пройдя через матрицу ОНВ, поступает в камеру смешения эжектора 8, где смешивается с потоком ОГ из турбины.
Для определения условий максимальной эффективности системы необходимо определить располагаемую работу L п и полезную работу L , которые можно получить, используя возможности данной системы. В соответствии со вторым законом термодинамики полностью преобразовать теплоту, полученную системой от источника, в полезную работу не представляется возможным. Поэтому полезная работа, получаемая при переходе системы из неравновесного (I) состояния в равновесное (II) состояние с окружающей средой, определится [6, 7]
L = ( U - U 0 ) - T o ( S 0 I - S I ) - p о ( V o - V ) , (1)
где U , V - энергия и объём некоторого источника в неравновесном состоянии; U 0 , V 0 - энергия и объём некоторого источника в равновесном состоянии; Т 0 , р 0, S о - температура, давление и энтропия окружающей среды.
В результате протекания обратимых процессов энтропия изолированной системы не меняется. Это означает, что изменение энтропии источника равно изменению энтропии окружающей среды, т. е. S I — S I = S — So . Используя это условие, можно определить располагаемую работу L п источника теплоты:
L п = ( U- U^ - T ) (S - - о ) - МК ) - Ю = / - ' о - T ) (S - So) , (2)
где 1 , 1 0 - энтальпия источника соответственно в неравновесном и равновесном состояниях со средой.
Связь между располагаемой и полезной работой выражается зависимостью [8, 9]:
L — L п = T 0 A S , (3)
где A S = ( S q — S‘ I ) — ( S — S o) - изменение энтропии системы.
Обратимыми процессами при наличии в системе одного холодного источника теплоты с неизменной температурой (окружающей среды с температурой T 0) являются адиабатический и изотермический процессы при температуре T 0.
Анализируя уравнение (2), можно отметить два крайних случая равновесия:
-
1) термическое равновесие (температура источника равна температуре среды Т т = Т 0):
L п = ( UuU(-tTs(-sS(==4 F,
полезная работа равна изменению так называемой энергии Гельмгольца F ;
-
2) механическое равновесие (давление источника равно давлению среды р т = р 0):
L п = ( --UU-po0Vo-V= = A Ф, полезная работа равна изменению так называемой энергии Гиббса Ф.
Если же источник теплоты (например, отработавшие газы) находится в тепловом и в механическом неравновесном состояниях с окружающей средой (р т ^ р 0 и Т т ^ Т 0), то максимальная полезная работа будет представлять собой сумму работ двух обратимых процессов: адиабатического процесса расширения 1-а до температуры Т 0 и изотермического процесса сжатия средой а -2 до
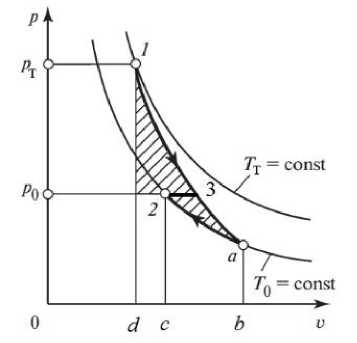
давления р 0. Это есть заштрихованная площадь на рис. 2. Несмотря на то, что цикл с перерасширением 1-3 - а -2 теоретически осуществим, в рассматриваемой системе он технически затруднен.
Рис. 2. p, v- диаграмма состояния газового потока, иллюстрирующая располагаемую работу при переходе системы из неравновесного ( р т , Т т ) состояния в равновесное ( р 0 , Т 0 ) состояние с окружающей средой
Fig. 2. p , v is a diagram of the state of the gas flow, illustrating the available operation during the transition of the system from a nonequilibrium ( р t , T t ) state to an equilibrium ( p 0 , T 0 ) state with the environment
Поэтому располагаемая работа, которая может быть получена в представленной выше структурной схеме системы, есть работа адиабатного расширения 1 -3 до давления окружающей среды. Для определения энергетических параметров элементов системы эжекционного охлаждения наддувочного воздуха обозначим через р с давление газа на выходе из выпускного трубопровода
(в отсутствие какого-либо дополнительного сопротивления р с ~ р о ), а через р т и Т т - давление и температуру газа перед газовой турбиной.
Примем для исследуемых случаев значения этих параметров неизменными, поэтому располагаемая работа Н п турбины также будет неизменна:
H п =
k
k
-
RT
т
т
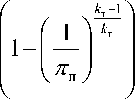
где k т, R т - показатель адиабаты и универсальная газовая постоянная отработавших газов; Т т - температура отработавших газов на входе в турбину; п п = р т /р с - степень понижения давления газов в турбине.
Результаты и обсуждение
Располагаемая работа турбины расходуется на привод компрессора и, как следствие, на повышение плотности воздуха после компрессора. Однако добиться этого можно следующими способами [5]:
-
1) полностью используя энергию отработавших газов только в турбине для повышения давления воздуха в компрессоре без его охлаждения;
-
2) частично используя энергию ОГ в турбине для повышения давления воздуха в компрессоре и частично в эжекторе - для осуществления циркуляции ОВ через ОНВ для понижения температуры НВ;
-
3) полностью используя энергию ОГ в турбине для повышения давления воздуха после компрессора, при этом осуществляя циркуляцию охлаждающего воздуха через ОНВ для понижения температуры НВ, например с использованием приводного вентилятора.
В данной статье рассмотрены первые два способа. Так, если степень повышения давления в компрессоре при первом способе составляет, например для дизеля 4ЧН13/15, п к = 2,86 и охлаждение воздуха после компрессора отсутствует, то его температура Т к1 = Т к составит 440 К при мощности дизеля N e ~ 250 кВт.
Особый интерес представляет второй способ, поскольку предполагает использование эжекцион- ного устройства для реализации низкопотенциальной энергии отработавших газов дизеля. Для оцен- ки эффективности второго способа требуется дополнительное исследование, поскольку речь идет о компромиссном распределении энергии отработавших газов между газовой турбиной и эжектором.
Обозначив давление ОГ перед эжектором через р р , можно определить работу газовой турбины [10, 11]:
H = — RT т k т - 1 т т
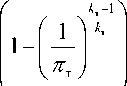
где
п т = р т/ р р - степень понижения давления газов в турбине.
Работа адиабатного расширения отработавших газов в эжекторе в таком случае запишется
H э =
k
k
—
R т T р
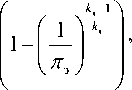
где пэ = р р/р с - степень понижения давления в эжекторе; Тр - температура отработавших газов на входе в эжектор.
Полагая п = —п и т = T , можно записать э пт р п э т
H э
= Н п
—
Н т =
Процессы, происходящие в элементах системы, можно проиллюстрировать на i, s -диаграмме состояния газовоздушных потоков (рис. 3). Далее параметры с индексом «р» будут относиться к рабочему (ОГ), а с индексом «н» - к эжектируемому (ОВ) потокам газов перед эжектором.
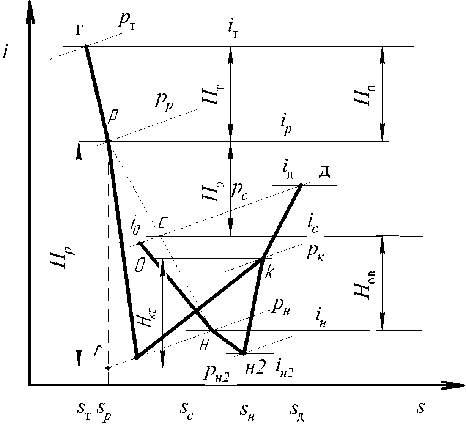
Рис. 3. i, s -диаграмма состояния газовоздушных потоков в системе «газовая турбина – эжектор – охладитель наддувочного воздуха», индексы «т» – состояние ОГ перед турбиной, «р» – состояние ОГ перед эжектором, «0» – состояние ОВ перед ОНВ, «н» – состояние ОВ перед эжектором, «к» – состояние смешанного потока в конце камеры смешения и «д» – на выходе из диффузора эжектора
Fig. 3. i , s -diagram of the state of gas-air flows in the system “gas turbine – ejector – charge air cooler”, indexes “t” – state of exhaust gas in front of the turbine, “p” – state of exhaust gas in front of the ejector, “0” – state of exhaust gas in front of the exhaust gas, “h” – state of exhaust gas before ejector, “k” – the state of the mixed flow at the end of the mixing chamber and “d” – at the outlet of the ejector diffuser
Поток отработавших газов, расширяясь от давления р р до давления р с, совершает работу, которая на диаграмме представлена разностью энтальпий [6]:
H э = i р - i с ,
где i p, i c - энтальпия потока отработавших газов соответственно до и после эжектора.
Эта работа идет на сжатие охлаждающего воздуха в эжекторе от давления р н до давления р с:
H ов = i c
—
i н
где п ов = р с/ р н - степень повышения давления охлаждающего воздуха в эжекторе.
Запишем уравнение энергетического баланса для эжектора [12, 13]:
G or H э = Gw H ов ,
где G ог и G ов - расход отработавших газов и охлаждающего воздуха соответственно.
Поделим обе части равенства на G ог:
Ст
Hов э H ов •
G ог
Отношение Gов/Gог обозначим через и и назовем теоретическим коэффициентом эжекции u = G- = H = iP-ic.. (14)
С ог H ов i c - i н
Уравнения (10)-(14) относятся к идеальному эжектору. Действительные же процессы протекают с потерями, а, соответственно, при заданном фиксированном давлении р с действительный коэффициент эжекции и д будет меньше теоретического и определится в соответствии с уравнением (2) как
u
д
i p - i c - T o ( s p - s c )
i c - i K - T 0 ( s c - s н )
где s p, s н , s с - удельная энтропия ОГ, ОВ и смешанного газовоздушного потока соответственно.
Уравнение (12) представляет собой закон сохранения энергии для процессов в эжекторе. Для описания процесса смешения в смесительной камере эжекционного устройства используют ещё два уравнения:
-
1) уравнение сохранения массового расхода [14, 15]:
-
G , + G . = G c = ( 1 + и ) G , • (16)
где G с - массовый расход смешанного потока из отработавших газов и охлаждающего воздуха.
-
2) закон сохранения импульса для любого поперечного сечения камеры смешения в эжекторе [16, 17]:
I = Gw + pf = const, (17)
где р - давление в поперечном сечении f камеры смешения, f - площадь поперечного сечения, w - скорость газа в поперечном сечении f камеры смешения.
Рассмотрим совместную работу эжектора с охладителем наддувочного воздуха. Уравнение энергетического баланса для охладителя наддувочного воздуха, учитывая уравнение (14), запишем в виде [18, 19]
G в c нв Л T = G„ис ;в ( Т 0 - Т н ) , (18)
где G в - расход наддувочного воздуха; с нв , с ов - удельная изобарная теплоемкость соответственно наддувочного и охлаждающего воздуха.
Пренебрегая разницей удельных теплоемкостей наддувочного и охлаждающего воздуха и полагая здесь и в дальнейшем, что G в ~ G ог, получим
Л Т = и ( Т 0 - Т н ) . (19)
В приведенном уравнении явно не учитывается зависимость А Т в функции начальной разности температур ( Т к] - Т 0 ), в отсутствие которой теплообмен между наддувочным и охлаждающим воздухом в принципе невозможен [14].
Результатом численного решения прямой задачи для системы уравнений (12), (17), (18) будет зависимость u = f ( Р р, Тр, Р н, Тн ), которую можно записать в виде [20]
и =
p * лнР ТК
p* (f 3p 1) q ( Яр) Pi
На рис. 4 представлены поля скоростей потоков отработавших газов и охлаждающего возду- ха, а также изменение давления вдоль оси эжектора.
Если пренебречь разницей теплофизических параметров газового и воздушного потоков, т. е. положить кр = кн и R р = R н, то выражение (20) запишется u = Пр
А(f’ -1)
qM. q ( я ) ,
где 0р - отношение критической скорости ОВ к критической скорости ОГ; Пр = р н /р р - отношение давлений ОГ и ОВ на срезе сопла; f3p = f3fp - отношение площадей КС и сопла; q ( Л н), q ( А р ) - газодинамические функции расхода от приведенных скоростей Л н и А р воздушного и газового потоков.
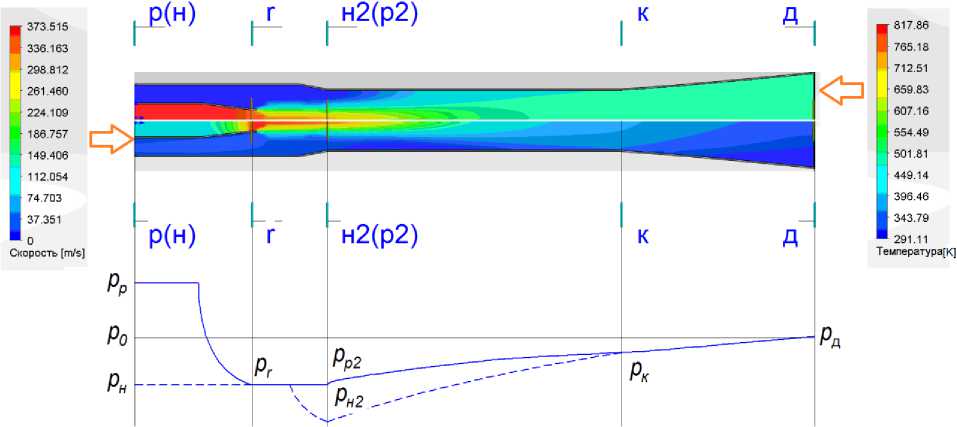
Рис. 4. Изменение основных параметров газовоздушных потоков вдоль оси эжектора в сечениях: «p» – перед эжектором, «r» – срез сопла, «н 2 (р 2 )» – начало камеры смешения, «к» – конец камеры смешения, «д» – конец диффузора
Fig. 4. Changes in the main parameters of gas–air flows along the ejector axis in sections: ”p” – in front of the ejector, “r” – nozzle section, “h 2 (p 2 )” – the beginning of the mixing chamber, “k” – the end of the mixing chamber, “d” – the end of the diffuser
Соотношения (20), (21) связывают коэффициент эжекции с параметрами потоков на входе в КС и отношением площадей КС и сопла. При заданном отношении давлений ОГ и ОВ коэффициент эжекции пропорционален корню квадратному из отношения температур смешивающихся потоков. Коэффициент эжекции увеличивается при повышении температуры рабочего потока и уменьшается при повышении температуры инжектируемого потока [4, 12].
Анализируя приведенные уравнения, можно заметить, что эжекционное устройство обладает следующим свойством: давление р н и температура Т н охлаждающего воздуха перед эжектором закономерно связаны с коэффициентом эжекции, т. е. р н = f( u). В свою очередь коэффициент эжекции и определяется как функция преимущественно от р р и Т р .
Проведенное исследование свидетельствует о том, что:
-
- рассмотренные элементы системы эжекционного охлаждения служат для повышения плотности наддувочного воздуха: турбина - посредством увеличения работы компрессора и, как следствие, повышения давления наддува р к, а эжектор - посредством снижения температуры наддувочного воздуха T k за счет обеспечения необходимого циркуляционного расхода G ов охлаждающего воздуха;
-
- сложность термодинамических связей параметров газовоздушных потоков в газовой турбине, эжекторе и охладителе наддувочного воздуха как в элементах рассматриваемой термодинамической системы и в связанных с ней воздушном компрессоре и дизеле существенно усложняет оценку их однозначного влияния на показатели рабочего цикла дизеля в целом;
-
- увеличение р р и Т р и, как следствие, энергии, подводимой потоком ОГ к эжектору, повышает коэффициент эжекции и, соответственно, расход охлаждающего воздуха через ОНВ. При этом снижается температура наддувочного воздуха после компрессора Т кь
-
- повышение р р и Т р перед соплом эжектора, очевидно, приводит к уменьшению степени понижения давления п т в турбине, т. е. к уменьшению её мощности, а следовательно, и работы компрессора. Это также приводит к уменьшению температуры Т к1 , но уже вследствие снижения степени повышения давления п к , что нерационально;
-
- в дальнейшем в зависимости от поставленных целей совершенствования системы эжекци-онного охлаждения наддувочного воздуха целесообразно принятие компромиссных решений, при которых система может обеспечить максимальную плотность наддувочного воздуха при минимальных затратах энергии на циркуляцию охлаждающего воздуха через матрицу охладителя по сравнению, например, с вентиляторной системой охлаждения;
-
– возможность достижения максимальной мощности дизеля при использовании эжектора для циркуляции охлаждающего воздуха через матрицу ОНВ требует дополнительного рассмотрения.
Список литературы Термодинамика системы "газовая турбина - эжектор - охладитель наддувочного воздуха" в дизеле с наддувом
- Heireth H., Prenninger P. Charging of internal combustion engine/ Springer Wien NewYork. 2003. 283 p.
- Ханин Н.С., Аболтин Э.В., Лямцев Б.Ф. Автомобильные двигатели с турбонаддувом: производственное издание. М.: ЭКОЛИТ, 2016, репринт.
- Двигатели внутреннего сгорания: Теория поршневых и комбинированных двигателей: учеб. для вузов по специальности «Двигатели внутреннего сгорания» / под общ. ред. А.С. Орлина, М.Г. Круглова. М.: Машиностроение, 1983. 372 с.
- Лазарев Е.А., Помаз А.Н. Эффективность эжекционного охлаждения наддувочного воздуха и особенности ее экспериментальной оценки // Вестник ЮУрГУ. Серия «Машиностроение». 2016. Т. 16, № 3. С. 21–28. DOI: 10.14529/engin160303
- Пат. РФ 2301899 Российская Федерация, F02B 37/12 Способ и устройство управления газообменом в дизеле с газотурбинным наддувом / Е.А. Лазарев, А.А, Малоземов, В.Н. Бондарь и др.; патентообладатель: ООО «Федеральный учебный межвузовский научный производственный центр» – № 2006100153/06 заявл. 10.01.2006; опубл. 17.06.2007, Бюл. № 18. 9 с.
- Кириллин В.А., Сычев В.В., Шейдлин А.Е. Техническая термодинамика. М.: Изд-во МЭИ, 2008. 494 с.
- Foust H. Thermodynamics, Gas Dynamics, and Combustion. Springer, 2021. 361 p.
- Двигатели внутреннего сгорания: Системы поршневых и комбинированных двигателей: учеб. для вузов по специальности «Двигатели внутреннего сгорания» / под общ. ред. А.С. Орлина, М.Г. Круглова. – М.: Машиностроение, 1985. 456 с.
- Rathakrishnan E. Applied Gas Dynamics. Wiley, 2019. 570 p.
- Байков Б.П. Турбокомпрессоры для наддува дизелей: справочное пособие. Л.: Машиностроение, 1975. 200 с.
- Gambini M., Vellini M. Turbomachinery: Fundamentals, Selection and Preliminary Design (Springer Tracts in Mechanical Engineering). Springer, 2021. 406 p.
- Соколов Е.Я., Зингер Н.М. Струйные аппараты. М.: Энергоатомиздат, 1989. 352 с.
- Bowden-Smith E. The Efficiency of Pumps and Ejectors. Legare Street Press, 2022. 224 p.
- Нащокин В.В. Техническая термодинамика и теплопередача: учебное пособие для не-энергетических специальностей вузов. М.: Высшая школа, 1975. 496 с.
- Babu V. Fundamentals of Gas Dynamics. Springer, 2020. 281 p.
- Черный Г.Г. Газовая динамика: учебник для университетов и втузов. М.: Наука. Гл. физ.-мат. лит., 1988. 424 с.
- Zucker R., Biblarz O. Fundamentals of Gas Dynamics. Wiley, 2019. 541 p.
- Михеев М.А., Михеева И.М. Основы теплопередачи. М.: Энергия, 1977. 344 с.
- Heywood J. Internal Combustion Engine Fundamentals. McGraw Hill, 2018. 1056 p.
- Абрамович Г.Н. Прикладная газовая динамика. М.: Наука. Гл. ред. физ.-мат. лит., 1991. 600 с.


