Термоупругодинамическая неустойчивость решения контактной задачи для покрытия с учетом тепловыделения от трения
Автор: Зеленцов Владимир Борисович, Митрин Борис Игоревич, Волков Сергей Сергеевич, Васильев Андрей Сергеевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 4 (79) т.14, 2014 года.
Бесплатный доступ
Рассматривается одномерная задача термоупругости о вертикальном внедрении жёсткой полуплоскости, движущейся горизонтально с постоянной скоростью по поверхности упругого покрытия (полосы в плане), нижняя сторона которого жестко оперта на недеформируемое основание. На поверхности основания поддерживается постоянная температура. Тепловой поток, порожденный фрикционным контактом, направлен в покрытие. Решение задачи получено с помощью интегрального преобразования Лапласа и представлено в виде контурных интегралов. Исследовано расположение полюсов подынтегральной функции решения в комплексной плоскости при различных значениях параметров задачи. Распределения температуры, смещений и напряжений по толщине покрытия получены в виде бесконечных рядов по собственным функциям. Показана неустойчивость полученных решений задачи на всём интервале времени при любой скорости скольжения полуплоскости по поверхности покрытия.
Термоупругодинамическая неустойчивость, связанная задача термоупругости, фрикционный контакт, покрытие
Короткий адрес: https://sciup.org/14250104
IDR: 14250104 | УДК: 539.3 | DOI: 10.12737/6910
Текст научной статьи Термоупругодинамическая неустойчивость решения контактной задачи для покрытия с учетом тепловыделения от трения
Постановка задачи.
Для исследования динамики скользящего фрикционного термоупругого контакта рассматривается одномерная задача плоской деформации о скольжении с постоянной скоростью I/ жесткой полуплоскости
В (h < х
< да) по поверхности
(х
= А) упругого покрытия в виде бесконечной полосы шириной
h
(0
Рис. 1. Схема скольжения жесткой полуплоскости по поверхности упругого покрытия, жестко соединенного с недеформируемым основанием
* Работа выполнена при поддержке грантов РФФИ № 14-08-91166-ГФЕН_а, 14-07-00271-а и 14-07-00705-а.
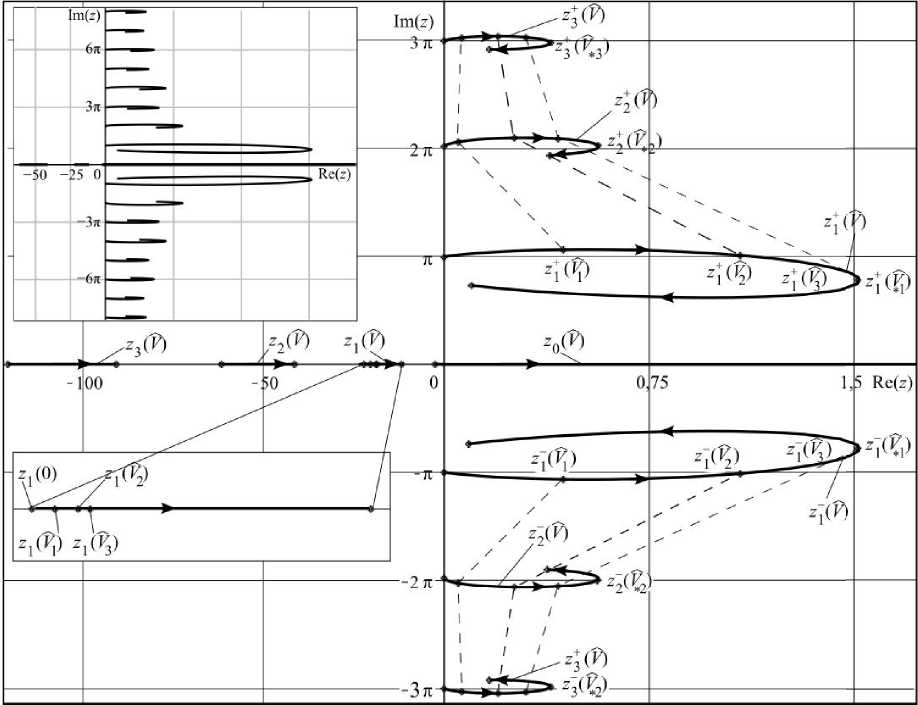
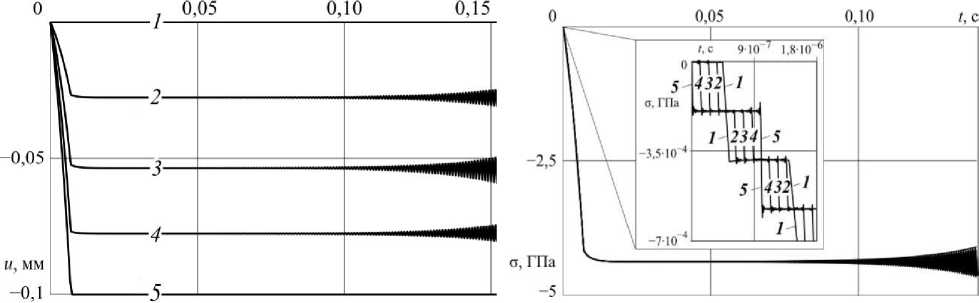
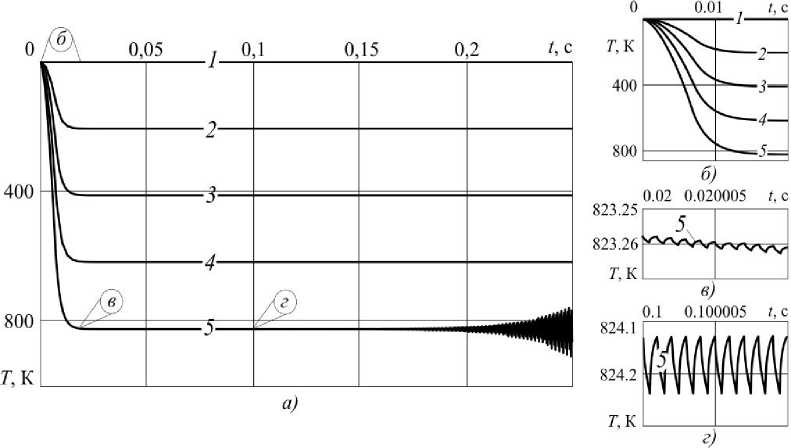
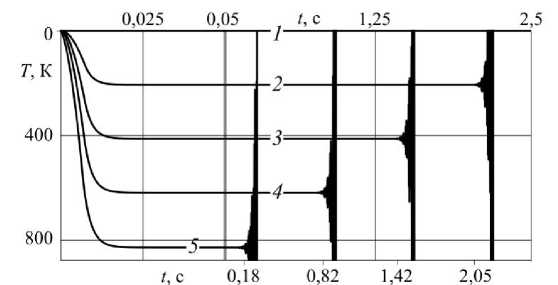
Скольжение недеформируемой полуплоскости В по поверхности покрытия происходит с учетом кулоновского трения, но без учета износа покрытия. Полуплоскость В деформирует упругое покрытие, смещаясь вдоль оси х по закону и(h,t) = -B(t), 0>0, где u{h,t") - вертикальное смещение поверхности покрытия при x = h. В начальный момент температура покрытия нулевая: Т(%,0) = Т0 = 0 (0 , би (х,0) _ и(Х,0) = = 0 . dt Сформулированная одномерная задача о скользящем контакте приводит к следующим граничным условиям: x = h: t/(/7,f) = -A(f), К°Т (h,t) =-fVb(h,t), 0>0; (1) бх х = 0: L/0O,t) = 0, T(0,f) = 0, 0>0, (2) где о(x,t) - напряжения сжатия в покрытии, К- коэффициент теплопроводности материала по крытия, д(t) - закон внедрения полуплоскости В в упругое покрытие, который принимается в следующем виде 0, Д(t) = Д0 -1 + e£t, 1, -со £> 0, где £> 0, t6 = E'h 2, Д0 - глубина внедрения полуплоскости В в упругое покрытие (0<Д0< hy Скорость внедрения полуплоскости В определяется как производная А(Г) и выражается формулой — со < t < 0, 0 0, A(t) = Д0- £e£t, 0, Максимальная скорость внедрения достигается при t = tE и составляет A(tE) = 2Д0£, при этом начальная скорость внедрения равна А(0) = v0 = £Д0, откуда £ = И0/Д0 (при заданных v„ и ^0)• Изменение и(x,t) и o(x,f) в полосе описывается одномерным уравнением теории упругости [10] --р—г = 0, 0<х —7---— = 0, 0<Х , Связь между о(x,t)- u^x,t) и Т^х,^ устанавливается соотношением Дюамеля - Неймана [12] , .. 2и(1- v) du 2и(1 + v) .. и (Л ,L ) — - U / (Л , L ) , 12 12 , , ала покрытия соответственно. Для удобства построения решения задачи (1) - (6) выражение о(x,t) (7) подставляется в дифференциальное уравнение движения упругой среды (5). В результате этого получим дифферен циальное уравнение движения упругой среды относительно и(x,t) и T^x,t^ 5 24/ 1524/_1 + у5Г Q , 0 , 0, , бх2 a2 dt2 1-v ОХ Vp(1-2v) где а - скорость упругой волны. Начальные условия на и(x,t)- T{x,t} и A(f) нулевые и(х,0} = 5^,0)=о, Т^О) = 0, 0<х Таким образом, решение рассматриваемой задачи, с учетом начальных условий (9), сводится к решению дифференциальных уравнений (6), (8) с граничными условиями (1), (2), а о(x,t) в (1) определяется формулой (7). - ча (1)-(9) относится к разряду собственно-связанных задач термоупругости, так как o связаны не только в формулах (5) и (7), но и во втором граничном условии (1). Её решение может быть построено различными методами математической физики [11]. С помощью интегрального преобразования Лапласа [13] решения поставленной задачи (1)-(9) 7"(x,f), и^х,)-- o(x,f) определя ются с помощью контурных квадратур о (X,t) = - т (x,t) = Т^ЕмЧ^ D(/^; ^z^1 и ) exP^ ^z- ~-T-LK U (x,t) = -21-J D^Nu^x,z>R-^z) exp^t \h 2p (1- И) (1-21/ )h справедливых для 0 плексной плоскости, представляющий прямую линию, параллельную мнимой оси и отстоящую от неё на величину dt^, в которой с/выбирается таким образом, чтобы все полюса подынтегральных функ- , R (z) = (1-у2^) ch Jzsh^z-y/(ch Vz chyz-yVzsh 4zsh\z-1),(13) NT (x,z) = Vz^-y2z)chyzsh(Vzxh"x),(14) Nu(x,z) = 1-\2z)chVzsh(yzv/7"1)- cvU\Uzxh~h)chyz-yVzshVzshYZr/7"1)-ch^z(h-x)h"*)), (15) Na (x,z) = у z[y° (x,z)sh\z - ch(yzxh 1 )^(z)],(16) N0 (x,z) = ^ - y2z)chVzch(yzy/7-1)+ y^ (yVz(shVzch(Yzr/?"1) -sh(Vzxhh (chyz)- shh^z(h-x)h "*)), R^= sh^zR (z), Ao XD (z) = z"1^ exp^-ztJ-1)+(z - sfj^ - exp(- (z - sfK)f£K)) «W,t)=t- ---, где a - постоянная из (7), a - из (8), безразмерные параметры у и И определяются формулами к ^ _ /Уб 2у(1+и)Л , 12 Внеинтегральные слагаемые получены в формуле (12) в результате выделения обобщенных квадратур [14-16] с помощью выражения D(z)ch(yzx/? 1 )/shyz . Квадратуры в формулах (10)—(12) существуют при выполнении условия t>(h-x)/a и благо даря алгебраическому убыванию подынтегральных функций на бесконечности D (z)NT(x,z)R '(z) О при Iz^ ОО, D (z) Nu (x,z)R "1(z) Na (z,z)/^d(z) при | Z ^ OO . Исследование подынтегральных функций в формулах (10)—(12) показывает, что все они меро морфны в комплексной плоскости переменной интегрирования z = 5 + ^l, то есть имеют в качестве изолированных особых точек только полюсы, которые доставляются обращением в ноль знаменателей этих функций: R(z), Ro)z). Кроме того, следует отметить, что подынтегральные функции в (10)—(12) при z = 0 и z = у 2 обращаются в ноль. NT (z,0) = Nulx$ = NQ,x,^ = /?(0) = /?о(0) = 0, NT (х,у2)) = Nukx,y2)) = /Vo(x,y-2) = R (Y"2)= А’: (V 2) 0, причём Na(x,z) и /?c(z) имеют двукратный ноль при z= 0. В заключении этого пункта заметим, что выделение главной части поведения подынтегральной функции в формуле (12) для о(x,t) производилось с помощью трансформанты Лапласа решения соответствующей одномерной упругой задачи о внедрении недеформируемой полуплоскости В в упругую полосу на жестком основании. Нули функции R(z) в комплексной плоскости. Для вычисления контурных интегралов в формулах (10)-(12) методами теории функций комплексного переменного необходимо знание нулей функции R(z) и их свойств в комплексной плоскости. Нули функции R(z') из (13) определяются в комплексной плоскости z = E, + x\ из решения трансцендентного уравнения R (z) = (1-Y2-^) ch 4z shyz-yV^hJz chYZ-YVzshVzshYZ-1)= 0, (22) которое совпадает с соответствующим характеристическим уравнением [5]. При численном определении корней уравнения (22) в комплексной плоскости z = ^ + /q использовались итерационные численные методы определения корней, требующие хорошего начального приближения. Для получения начального приближения корней уравнения применяется параметрический анализ функции R(z) по двум безразмерным параметрам у и V . Зафиксировав у и положив / = 0 в (22), получим упрощенное уравнение (1 - y2z)chVzshyz = 0, (23) решение которого распадается на решение трех уравнений: 1-Y2z = 0, chVz = 0, shYZ = 0. (24) для любых у иV, но и всех остальных подынтегральных функций, что было отмечено ещё в (21) (12). Второе и третье уравнения в (24) приносят две бесконечные последовательности нулей z0k = "" 2 (1 + 2^) , к = 0,1,2,. z0„=±/y, /7 = 0,1,2,3,... 0 0 0 приближениями для последовательного с увеличением / определения соответствующих по номеру , = 0 , = фиксированных Y- Нули z0к = z^.(0) (25), соответствующие / = 0, располагаются на отрицательной части действительной оси Im(z) = n = 0 комплексной плоскости z = E, + k\. Множество z0(/) при /е[0,оо) представляет полубесконечный промежуток [z0(0),да) действительной оси, где z0(0) = -п2/4, а при V = 2 и произвольном y z0(Ю попадает в начало координат z0(2) = 0. Таким образом, при 0<1/<2 выполняется неравенство -п 2/4 < z0 (И) <0,апри V > 2 значения z0 (/)> 0 и располагаются на положительной части действительной оси (рис. 2). При этом z0(И) единственный из всех корней (22), который при произвольном у обладает свойством Jim z0(1/) = оо. Множества ^(и), к - 1 7 А fX X,“ , '-,,... , V е [0,оо) при произвольном у представляют собой отрезки на отрицательной части действительной оси, левый край которых совпадает с z0к = z^(0)< 0, к = 1,2,3,.., из выражения (25), а правый представляет точку сгущения Jim zk(/) = zk^>)>z^(0), rflez^(0)<0 (на рис. 2 стрел- кой указано направление расположения точек множества zk жительным направлением действительной оси). со, совпадающее с поло- 0 20 . Нули z0„ = z±(0) (26), соответствующие / = 0, располагаются на мнимой оси Re(z) = 5 = 0 , последовательного с увеличением / определения в комплексной плоскости соответствующих по номеру нулей z,,^ из численного решения уравнения (22). Ноль z00 z0(0) = 0 не является полюсом V е [0,ос) представляют в комплексной плоскости z = ^ + >q траектории в виде кривых линий, похожих на незаконченные эллипсы (см. рис. 2) с главными осями, параллельными действительной оси Im(z) = q = о. С ростом п эллип-(1 ширина с ростом номера уменьшается (рис. 2). Уменьшается с ростом номера п и Re(z^(l/))=^, то : lim Re(z±i/))= lim ^ = 0. На графиках z^) стрелками указано направление расположения нулей с ростом аргумента V, при- (/) возрастает и при V = V«n достигает чем при возрастании V от 0 до V•„ действительная часть z„ своего наибольшего значения. При дальнейшем увеличении V от V„n до се величина Re(z„(l/)) убывает до некоторого конечного значения Re(z±(oo)) (рис. 2). Рис. 2. Расположение нулей R(z) в комплексной плоскости z при V е [0, ос), у = 1. В левом верхнем углу - общий план расположения нулей, в нижнем левом углу — расположение множества точек z1(1/) в увеличенном формате Мнимая часть корней z„«/) уравнения (22) Im(z;;(l/))= п± с ростом п приближается к ± —, что также следует из уравнения (26): Im(?^)=^=±^ + O(1), п = 1,2,...(28) В этом случае для больших номеров п нули z^(/) можно записать в виде , YVyn/7 а корни z„^ при этом для больших значений п получат асимптотику /7 —---±/— + О — +/О(1) при Л—>оо. YVYn/7 y Vn) Следует заметить, что графики z„ и zn обладают симметрией относительно действительной оси Im(z) = q = о, как и подынтегральные функции в квадратурах (10)—(12), а для z„ выполняется равенство 7~ — 7* . На всех траекториях нулей z„(I/), п = 1,2,3,..., указаны точками значения гк(у^ и z±(l/7), где j = 1,2,3, при чём 1/1 = 1, /2 = 2, 1/3 = 2,7. Значения z±(l/,), п = 1,2,3,..., при одинаковых Vj, = 1,2,3 Графики нулей функции /?(z): z^(l/),z±(l/), n,k = 1,2,3,..., z0(l/), представленных на рис. 2, Maple количестве значащих цифр в расчетах. Анализ полученных решений. После вычисления контурных квадратур в комплексной плоскости в (10)—(12) [17,18] для функций 7"(x,f), u^x,t^ и o(x,f) получаются удобные для вычисления фор мулы в виде рядов по полюсам подынтегральных функций 1 0 T^l-lk—A^^ 0, 0, (33) 0, 0, (34) (35) 0 , 0, ' (х, Г) - . " " , / ,(х, Г l" \< V Гек, ~ ~ u(x,t) = -До^Sk(х,t^H((-1/"^ , 2р(1- v) До О (x,t) =--—----Г_2°. 1 - 21/ /7 Е ta Wn кх, 0)+ А^ ,Х, Г)))+ + (x,t) + s(k(x,~)>1 ((-1)^(f -f£KJ где Sk(x,t) (к = 1,2) выражаются формулами: Si(aV) = s^O + ^f) G^x ,t) =2 Re ^e(z^'(z^,x,f)+ ^VzkWk.x.t), 10 S2 (x, t) = S( (x , t) + G(x, t) - (G {x, t-t^, s 1 (x, t) = К(tKE,x, t)- К(0,%,0) , S((x,t) = K(0,x,0), (IS^SlZ^PYrA fA fx (Z^,!)— exp^ZTj, A (Z,X,L) — exppZT^ A (Z) (V) К (0,x,0)= lim N (x,z) R (z) 0 (z) = z^z-t^ Ь i^X,l) — ( Re/ti\Z(lk p\ \Z,k ,X,tj 00 0 Э 2 X ,L ) — (D1 X, L L^ K) D i \X, L ) , где R’(z) есть прюизводная no z, H(t) - функция Хэвисайда. В формуле (35) под A(f) понимается нормирюванная функция А(г) = Ее£{Н(^£ - t)H(t) из (4), где E = v0/Д0. Функция G(x,t) (37) в фор>мулах для Sk(x,t) (k = 1,() содержит два беско нечных ряда, один из которых по полюсам zk , к = 1,(,3,..., следующего вида 00 / \ ~ м(хх 5+= V h\x zt leZkt b(x z} - J Z-IU\ , UVX,Z)-Q\Z) /X , ~ сходимость которюго не очевидна, так как Re(z^)> 0, t > 0. С учетом асимптотики zk (31) пр>и ~1 к^сс можно показать, что последовательность экспонент ^е^ является ограниченной для ~ ~ ~ а р>яд (41) является сходящимся [19], в том числе за счет убывания 6(z) при |z| -> со . С другой сто-рюны, учитывая упорядоченность ^е^)|, где для двух соседних членов выполняется условие Dol Ро|7~*~ I О Re\-^^/>Re\^ £+1 )f К — 1,(,3,..., сумму ряда (44) можно приставить в виде 5+ В^х ,z) ,4 b^x ,z+J' где ряд в скобках является сходящимся, прячем со скорюстью геометрической прюгрюссии, так как ~ Re(zf -zk)>0, к = (,3,... Из выражения (42) вытекает, что пр>и неограниченном возрастании t (t -»оо), неограниченно возрастает S+ из (41), а решение, его содержащее, является неустой- В формуле для G(x,f) (37) из Sk(x,t( (к = 1,(), крюме вышеупомянутого ряда (41), содер>- жится и др>угой бесконечный р>яд по полюсам zk ,к = 0,1,(,3,... Учитывая свойства 0 0 2 0 0 2 02 0, 2 00 ~ С- - у Z 3 ~ ^^ ,ZkF , где b(x,z^ из выражения (41) для фиксированных значений ~ сходится со скоростью геометриче- 2 00 рестроенная по формуле ~ ~ ~ ~ , 1 , , где В^х,z) из (41), при ~ -> ос неограниченно возрастает, хотя ряд, стоящий в скобках, сходится. решения рассмотренной задачи (33)-(35), содержащие ряды (41) и (43), являются термоупругоне-0. Численный анализ полученных решений. Для детального изучения термоупругонеустойчивого решения рассматриваемой задачи используются формулы (33)-(35). Числовые значения параметров = 44 109 2, = = 1,04 10 5 1, = 4 103 = 8 10 4 2 = 62,8 = 0,15, б0=0,1h, i/0 = 0,01 м/с, Д = 2-10“3м, V= 1,58 м/с, t£ = 6,93-10 3с, Л^ 5-10 7 с, в результате чего безразмерные параметры задачи у и / приобретают следующие значения: у = 1,0-10"4 и V = 0,25. На рис. 3 представлены графики изменения смещений и(x,t) по толщине покрытия (0 ростью геометрической прогрессии развивается амплитуда смещений неустойчивого и(x,t) на собственной частоте Im(z^), теряя физический смысл с некоторого момента = 0,5 На рис. 4 приведены графики изменения напряжений о(x,t) для различных глубин решения времени, ПО X, ко- торые, как и на рис. 3, обозначены цифрами 1-5. Начиная с некоторого момента времени, амплитуда колебаний о(x,t) на собственной частоте Im(z^) нарастает по экспоненте и неустойчивое решение теряет физический смысл, причем примерно в тот же временной период, когда это же происходит со смещениями u(x,t) на рис. 3. С помощью врезки на рис. 4 подробно показано изменение величины напряжений о(x,t) на отрезке fe[0, 1,8-10"6] в более мелком временном масштабе: различается = = кого основания (две цифры 1 на одной и той же прямой), двумя цифрами 5 отмечается рост амплиту-= На рис. 5, а представлены графики температуры т(x,t) в покрытии для различных значений ,, ные фрагменты графиков температуры т(x,t) в более мелком временном масштабе: на врезке бда- , график с цифрой 1 соответствует выполнению при х = 0 граничного условия 7"(0,f) = 0, с увеличением % графики т(x,t) показывают всё более быстрое нарастание температуры с максиму- мом на контакте при х = h (кривая 5); на врезке в представлен график температуры T{h,t) (на кон-3 частоте Im(z(); на врезке г показан интервал времени, на котором амплитуда колебаний претерпела 50-кратное увеличение по сравнению с врезкой в. Рис. 3. Графики распределения смещений u(x,t) по толщине Рис. 4. Графики распределения напряжений c(x,t) по толщине покрытия покрытия Рис. 5. Графики температуры ДхД на разных глубинах по толщине покрытия и на различных временных интервалах В дальнейшем (рис. 6) можно видеть экспоненциальное развитие амплитуды колебаний графика 7(h,t), достигающей десятков градусов, что свидетельствует о потере физического смысла для х = h при t > 0,18 с, для х = 0,15h - при t> 0,82с, для х = 0,5h - при t > 1,42 с, для х = 0,25h- при t > 2,05 с. Такая зависимость нарушения физического смысла оказалась свойственной только температуре, определяемой из параболического дифференциального уравнения. Рис. 6. Температура 7(х, кием времени потери физического смысла Выводы. Термоупругодинамическая неустойчивость скользящего фрикционного контакта при движении жесткой полуплоскости по упругому покрытию на жестком основании наступает при любой скорости движения полуплоскости. Неустойчивость решения рассмотренной задачи о скользящем фрикционном контакте заключается в том, что, начиная с некоторого момента времени, полученное решение теряет физический смысл - амплитуда собственных колебаний неограниченно возрастает по времени. Следует заметить, что решение задачи для смещений и напряжений теряет физический смысл раньше, чем решение для температуры, что может быть существенным моментом при разработке методов диагностики возникновения термоупругодинамической неустойчивости скользящего контакта.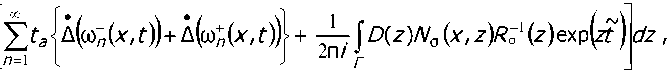
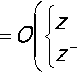
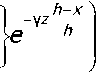
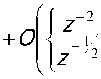
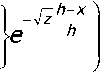
1/)=^±/^, /7 = 1,2,... (29)
где lim ^ = 0 из (27). Подставив (29) в уравнение (22) и считая при этом ^ малой величиной, для больших /7 получим следующую оценку:

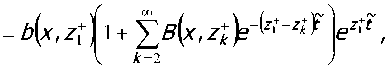
Список литературы Термоупругодинамическая неустойчивость решения контактной задачи для покрытия с учетом тепловыделения от трения
- Barber, J. R. Thermoelastic instabilities in the sliding of conforming solids/J. R. Barber//Proceedings of the Royal Society A. -1969. -Т. 312. -С. 381-394.
- Dow, T. A., Thermoelastic instability of sliding contact in the absence of Wear/T. A. Dow, R. A. Burton//Wear. -1972. -Т. 19. -С. 315-328.
- Burton, R. A. Thermoelastic instability in a seal-like configuration/R. A. Burton, V. Nerlikar, S. R. Kilaparti//Wear. -1973. -Т. 24. -С. 177-188.
- Barber, J. R. Stability considerations in thermoelastic contact/J. R. Barber, J. Dundurs, M. Comninou//Transactions ASME. Journal of Applied Mechanics. -1980. -Т. 47, вып. 4. -С. 871-874.
- Afferrante, L. Sliding thermoelastodynamic instability/L. Afferrante, M. Ciavarella, J. R. Barber//Proceedings of the Royal Society A. -2006. -Т. 462. -С. 2161-2176.
- Моров, В. Н. Термоупругая неустойчивость фрикционного контакта штампов с полупространством/В. Н. Моров, И. Н. Черский//Трение и износ. -1985. -Т. 6, № 1. -С. 27-38.
- Interaction of thermal contact resistance and frictional heating in thermoelastic instability/M. Ciavarella //International Journal of Solids and Structures. -2003. -Т. 40, вып. 21. -С. 5583-5597.
- Moirot, F. Brake squeal: a problem of flutter instability of the steady sliding solution/F. Moirot, Q. S. Nguyen//Archives of Mechanics. -2006. -Т. 52. -С. 645-662.
- Kinkaid, N. M. Automotive disk brake squeal/N. M. Kinkaid, O. M. O’Reilly, P. Papadopoulos//Journal of Sound and Vibration. -2003. -Т. 267. -С. 105-166.
- Лурье, А. И. Теория упругости/А. И. Лурье. -Москва: Наука, 1979. -979 с.
- Тихонов, А. Н. Уравнения математической физики/А. Н. Тихонов, А. А. Самарский. -Москва: Наука, 1977. -735 с.
- Новацкий, В. Вопросы термоупругости: пер. с польского/В. Новацкий. -Москва: Изд-во АН СССР, 1962. -363 с.
- Диткин, В. А. Интегральные преобразования и операционные исчисления/В. А. Диткин, А. П. Прудников. -Москва: Физматлит, 1961. -524 с.
- Функциональный анализ/Н. Я. Виленкин . -Москва: Физматлит, 1961. -524 с.
- Бейтмен, Г. Высшие трансцендентные функции/Г. Бейтмен, А. Эрдейи. -Москва: Наука, 1965. -Т. 1. -296 с.
- Брычков, Ю. А. Интегральные преобразования обобщенных функций/Ю. А. Брычков, А. П. Прудников. -Москва: Наука, 1977. -288 с.
- Гурвиц, А. Теория функций/А. Гурвиц, Р. Курант. -Москва: Наука, 1968. -648 с.
- Титчмарш, Е. Теория функций/Е. Титчмарш. -Москва: Наука, 1980. -464 с.
- Бриллинджер, Д. Временные ряды/Д. Бриллинджер. -Москва: Мир, 1980. -536 с.
- Barber, J. R. Thermoelastic instabilities in the sliding of conforming solids. Proceedings of the Royal Society A. 1969, vol. 312, pp. 381-394.
- Dow, T. A., Burton, R. A. Thermoelastic instability of sliding contact in the absence of wear. Wear, 1972, vol. 19, pp. 315-328.
- Burton, R. A., Nerlikar, V., Kilaparti, S. R. Thermoelastic instability in a seal-like configuration. Wear, 1973, vol. 24, pp. 177-188.
- Barber, J. R., Dundurs, J., Comninou, M. Stability considerations in thermoelastic contact. Transactions ASME. Journal of Applied Mechanics. 1980, vol. 47, iss. 4, pp. 871-874.
- Afferrante, L., Ciavarella, M., Barber, J. R. Sliding thermoelastodynamic instability. Proceedings of the Royal Society A. 2006, vol. 462, pp. 2161-2176.
- Morov, V. A., Cherskiy, I. N. Termouprugaya neustoychivost' friktsionnogo kontakta shtampov s poluprostranstvom. Friction and Wear, 1985, vol. 6, no. 1, pp. 18-27 (in Russian).
- Ciavarella, M., Johansson, L., Afferrante, L., Klarbring, A., Barber, J. R. Interaction of thermal contact resistance and frictional heating in thermoelastic instability. International Journal of Solids and Structures, 2003, vol. 40, iss. 21, pp. 5583-5597.
- Moirot, F., Nguyen, Q. S. Brake squeal: a problem of flutter instability of the steady sliding solution. Archives of Mechanics, 2000, vol. 52, pp. 645-662.
- Kinkaid, N. M., O’Reilly, O. M., Papadopoulos, P. Automotive disk brake squeal. Journal of Sound and Vibration, 2003, vol. 267, pp. 105-166.
- Lourie, A. I. Teoriya uprugosti Moscow: Nauka, 1979, 979 p. (in Russian).
- Tikhonov, A. N., Samarskii, A. A. Equations of Mathematical Physics. Dover Books on Physics, 2011, 800 p.
- Nowacki, W. Thermoelasticity. Addison-Wesley Publishing Company, 1962. 628 p.
- Ditkin, V. A., Prudnikov, A. P. Integralynie preobrazovaniya i operacionnye ischisleniya Moscow: Fizmatlit, 1961, 524 p. (in Russian).
- Vilenkin, N. Y., Flaherty, R. E. Functional Analysis. Wolters-Noordhoff B. V., 1972, 394 p.
- Bateman, H., Erdelyi, A. Higher transcendental functions. Vol. 1. New York: McGraw-Hill, 1953.
- Brychkov, Y. A., Prudnikov, A. P. Integral Transforms of Generalized Functions. New York: Gordon and Breach Science Publishers, 1989, 343 p.
- Hurwitz, A., Courant, P. Teoriya funkciy. Moscow: Nauka, 1968, 648 p. (in Russian).
- Titchmarsh, E. C. The Theory of Functions (2nd edition). New York: Oxford University Press, 1976, 464 p.
- Brillinger, D. R. Time series: Data analysis and theory. New York: Holt, Rinehart & Winston, 1975.


