Тестовые испытания полупроводниковых тензорезисторов на основе тонких пленок SmS

Основным параметром тензорезистора является его коэффициент тензочувствительности K = = Δ R / ( R ∙ ε ), где R , Δ R и ε — электросопротивление, приращение электросопротивления и деформация датчика соответственно [1]. Для измерения этого параметра тензорезистор должен быть наклеен на балку с помощью достаточно жесткого связующего. Изгиб балки задает деформацию тен-зорезистора, приводящую к изменению его электросопротивления. Обе эти величины измеряются, и их соотношение определяет величину K . После проведения такого тестового испытания тензоре-зистор безвозвратно выходит из строя. Это создает проблемы в процессе разработки новых тензоре-зисторов, т. к. отсутствует возможность измерения каких-либо других параметров после калибровки. Помимо этого, в процессе промышленного производства резистивных полупроводниковых тензодатчиков некоторая их часть, представляющая случайную выборку из партии готовых изделий, изымается для проведения тестовых испытаний с целью определения средней по партии величины коэффициента тензочувствительности [1]. Поскольку повторное использование прошедших тестирование датчиков исключено, себестоимость единицы продукции увеличивается.

В производстве тонкопленочных тензорезисто-ров на основе полупроводниковых пленок SmS таких экономических потерь можно избежать, если полностью изменить процесс тестирования датчиков, сведя его к определению величины барического коэффициента сопротивления B = ∂ln R /∂ P

( P — давление) в гидростатической и химически инертной по отношению к материалу пленки среде, и уже далее путем перерасчета величины указанного параметра получать искомое значение K . Это принципиально возможно, поскольку в датчиках на основе SmS изменение удельной электропроводности обусловлено изменением удельного объема тензочувствительного слоя под действием деформации [2].

В настоящей работе приведен вывод соотношения между коэффициентом тензочувствительности K и барическим коэффициентом электросопротивления В для тонкопленочных тензо- и барорезисторов на основе SmS.

ВЫВОД СООТНОШЕНИЯ МЕЖДУ K И B

Коэффициент тензочувствительности K =

= A R / ( R • е ) = (A R / R ) / (A 1 / 1 ); е = A 1 / 1 = -P -; R =

E подл.

= ρl / S , где l — длина тензочувствительного слоя датчика (пленка SmS); S — площадь поперечного сечения пленки; E _п^Ю_одл. — модуль Юнга подложки; P _L — напряжение растяжения (сжатия) датчика, приложенное вдоль направления l ; ρ — удельное электросопротивление тензочувствительного слоя [1]. Путем несложных преобразований, учитывая различие упругих свойств материалов пленки SmS и подложки, получаем:

K = 1 + V sms

+ v ± E ^Ю —^^

подл. подл.

Р -9 P i

= 1 + v_{s s} + v   + E Ю

SmS подл. подл.

д о

' о -a p _l

= 1 + v _s + v   + E Ю

SmS подл. подл.

д n

' n -d P _L ,

= ^{1 + V} SmS ^{+ V} подл. ⁺

₊   1      ® 1/2 < Ц ’)    Z £ 1 Z j = 1 9

⁺ E пЮдл. kT-F /2 ( ц ’)    ( n + S )

где ν _SmS — коэффициент Пуассона поликристал-лической пленки SmS; ν _подл. — коэффициент Пуассона подложки; σ — удельная электропроводность пленки SmS и n — концентрация свободных носителей заряда (электронов проводимости) в ней. Замена σ на n допустима, поскольку подвижность электронов проводимости под давлением в SmS меняется слабо [3].

Согласно общепринятой модели электропереноса в SmS [4], электроны активируются в зону проводимости с различных донорных уровней, включая 4f-уровни, имеющих различные деформационные потенциалы Ξ i , где i — номер уровня. Парциальные концентрации электронов, активированных с этих донорных уровней, определяются величинами их деформационных потенциалов и сжимаемостью воспринимающей напряжения структуры.

Для одноосного сжатия (растяжения) относительное изменение объема:

где

^{X [1} - ^{( v} SmS ^{+ V} подл.^)] ,                               (4)

₉ , = KN, ( ц, E i )

i        d E'

*

ц = const

.    .    aNi ( ц, Ej )

; ^s i                   *

д ц

E i = const

;

N_i — концентрация электронов, активированных

в зону проводимости с

F ( ц *) =[---——-

^Y      0 1 + exp( x - ц )

i -го примесного уровня;

— интеграл Ферми сте-

A V         P l n          M

= + ^£ ii = ⁺ „Ю   ^{- [1  ( v} SmS ^{+ V} подл. )],

V             E подл.

пени γ ; f 0 = [1 + exp( x -–- μ ^*)]^–1 — функция распределения Ферми—Дирака; µ — химический потенциал; ц = ц / kT — приведенный химический потенциал; 0_У( ц *) = [ |-^ f ⁰ | x ^Y d x = F ,( д *) / Г( у + 1);

^Y     0 (5 x )

Г( γ + 1) — гамма-функция [6]; γ = 1/2.

Для барического коэффициента сопротивления _n 1 5 R   1 д n

B =---=--- по аналогии с (4) можно за-

R дPg n дPg писать:

где i =1, 2, 3 и по повторяющимся индексам предполагается суммирование. Сжимаемость в этом случае будет определяться выражением

B =     ® 1/2⁽ ц ‘)

kT - F 1/2 ( ц*)

mj

^Z, = 1 ^Z j = 1 ⁹ i ^E , _R

---;-----^eg =

( n + S )       g

d V 1

^в1 = V AD = 7Ю- ^{- [1} — ^{( V} SmS + ^V подл.^)] .        ⁽³⁾

^{V -д} P l    ^E подл.

-

E ^Ю подл.

-

® 1/2⁽ ц ‘) kT - F_m( Ц)

-

mj ^Z i = 1 ^Z J=1 ⁹ i -----------X

^{( n +} s )

Логарифмическую производную концентрации

свободных носителей тока по давлению

дn n -dPL

X

E ^Ю подл.

Ю

_ E SmS

+ 2 - ( 1

-

ν SmS

-

^{2 v} подл. ) ,

можно записать аналогично [5], обобщив приведенную там формулу на случай счетного числа m донорных уровней с деформационными потенциалами Ξ i и вырождением j ( i ). Тогда для коэффициента тензочувствительности K получаем вы-

где β_g — объемная сжимаемость.

Из (4) и (5) находим искомое соотношение между K и В :

ражение

K = ^{1 +} V SmS ⁺ V _П одл. +

^K = ^{1 +} V sms ⁺ V под _Л . +

+ B - E пЮдл.

_ ® 1 _/2( ц ’)    Z Г = 1 Z^ E i

+

kT - F 1/2 (ц * )      ( n + s )

- в 1 =

^[1 - ^{( V} SmS ^{+ V} подл.^)]

E ^Ю

E подл.

—Ю ^{+ 2} ( 1 ^V SmS ^{2 V} подл. ) E SmS

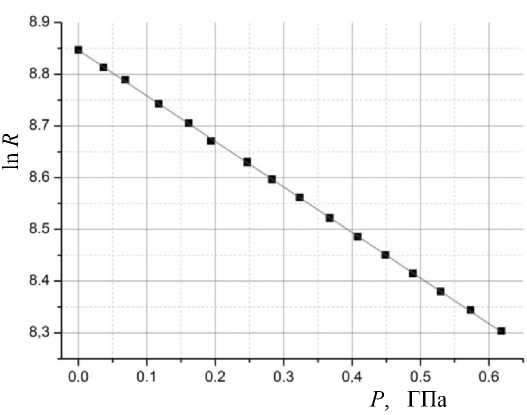
Рис. 1. Барическая зависимость логарифма электросопротивления R пленочного тензодатчика на основе SmS на подложке из константана

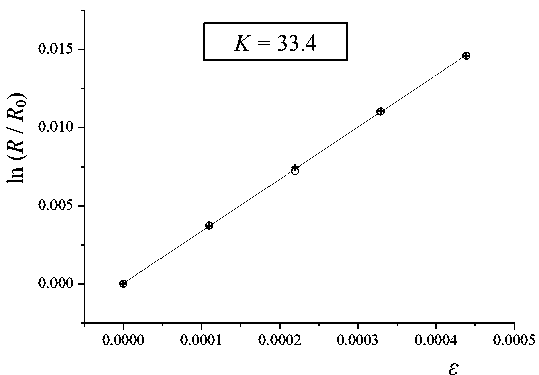
Рис. 2. Зависимость логарифма приведенного электросопротивления пленочного тензодатчика на основе SmS на подложке из константана от одноосной деформации

Обращает на себя внимание тот факт, что в конечную формулу (6) параметры зонной структуры пленки SmS уже не входят в силу изотропности тензо(баро)резистивного эффекта, в основе которого лежит сферическая симметрия строения дна зоны проводимости, образованного состояниями ионов Sm S-типа.

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ВЫВЕДЕННОГО СООТНОШЕНИЯ

Справедливость выражения (6) можно проверить экспериментально. C этой целью стандартный тензодатчик на основе пленки SmS, напыленной на металлическую константановую подложку через изолирующий слой SiO, был подвергнут гидростатическому сжатию в среде полиэтилсилоксановой жидкости ПЭС-5 до давления Р = 0.62 ГПa. Барическая зависимость логарифма электросопротивления пленки приведена на рис. 1. По наклону зависимости lnR(P) был определен коэффициент В = - 0.88 ГПа–1. Модуль Юнга мате- риала подложки (константана) EпЮодл. = 1.63∙1011 Па, коэффициент Пуассона — 0.33, модуль Юнга по-ликристаллического SmS ESЮmS = 0.83∙1011 Па, коэффициент Пуассона — 0.21 [7]. На основании этих данных по формуле (6) была рассчитана величина коэффициента тензочувствительности K, которая оказалась равной K = 33.2. Далее испытуемый образец был подвергнут одноосной деформации на установке для калибровки тензорези-сторов, и для него было получено значение K = 33.4. Как видно, величина коэффициента тен-зочувствительности K, рассчитанного по величине В, превосходно совпадает с его экспериментально определенным значением с точностью не хуже 1 %. Это дает возможность рассчитать и построить справочные таблицы перевода величин В в величины K для пленок SmS, напыленных на различные подложки. В приведенной таблице, в частности, представлены такие переводные данные для пленок SmS на стеклянной и константановой подложках.

Соответствие барических коэффициентов сопротивления В коэффициентам тензочувствительности K для поли-кристаллических пленок SmS на подложках из стекла и константана

B ∙10–3, MPa–1	K для подложки из стекла с параметрами: E Ю = 80 ГПa; ν = 0.2	K для подложки из константана с параметрами: E Ю = 163 ГПa; ν = 0. 33
1	2	3
0.5	14.9	19.54
0.6	17.6	23.14

Продолжение таблицы

1	2	3
0.7	20.3	26.74
0.8	23.0	30.34
0.9	25.7	33.94
1.0	28.4	37.54
1.1	31.1	41.14
1.2	33.8	44.74
1.3	36.5	48.34
1.4	39.5	51.94
1.5	41.9	55.54
1.6	44.6	59.14
1.7	47.3	62.74
1.8	50.0	66.34
1.9	52.7	69.94
2.0	55.4	73.54
2.1	58.1	77.14
2.2	60.8	80.74
2.3	63.5	84.34
2.4	66.2	87.94
2.5	68.9	91.54
2.6	71.6	95.14
2.7	74.3	98.74
2.8	77.0	102.34
2.9	79.7	105.94
3.0	82.4	109.54

Работа выполнена при поддержке фирмы SmStenzotherm GmbH .