Тетрация как специальная функция

Тетрация или суперэкспонента определяется как голоморфное решение F уравнения

F ⁽ z + 1)=ехр ь ( F ( z ) ) .                                  (1)

Такое уравнение рассматривалось с 1950-х гг. [1–10]. В частности, для «натурального» основания b = e. Термин «суперэкспонента», или sexp, указывает на то, что функция F является суперфункцией [ 9 , 11 ] от экспоненты.

Вообще говоря, для некоторой функции H , которую можно назвать передаточной функцией [ 11 , 12 ], суперфункция F есть голоморфное решение уравнения

F (z + 1) = H (F ( z )) .                                     (2)

Уравнение ( 1 ) является специальным случаем уравнения ( 2 ) для H = exp b . При этом умножение является суперфункцией сложения (прибавления константы), экспонента — суперфункцией от умножения на константу, а решение F уравнения ( 1 ) — суперфункцией от экспоненты, т. е. суперэкспонентой.

Специальный случай суперэкспоненты F , голоморфной хотя бы в правой части комплексной плоскости, я называю «тетрацией», F = tet b , если эта функция удовлетворяет дополнительному условию

F (0) = 1 .                                              (3)

Четыре примера таких функций показаны на рис. 1 для b = V2, b = exp(1 / e), b = 2 и b = e.

Тетрация tet b ( z ) может интерпретироваться как результат z -кратного экспоненциро-вания единицы, по крайней мере для целых значений z :

tet b ( z ) = exp b( exp b (.. exp _b (1)..) )

'-------------------------------------- -                                              (4)

z exponentiations

(c) 2010 Кузнецов Д. Ю.

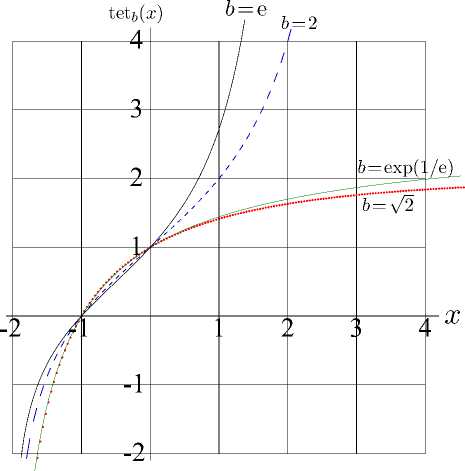
Рис. 1. Тетрация tet b (x) по основанию b = e (толстая сплошная), b = 2 (пунктир), b = exp(1/e) (тонкая сплошная) и b = V2 (точки) как голоморфное решение уравнений ( 1 ), ( 2 ) для вещественных значений x .

Имя функции «тетрация» («tetra» значит «четыре») указывает, что эта функция является четвертым элементом последовательности функций (единичный инкремент, сложение, умножение, экспонента, тетрация, пентация, . . . ), в которой каждый элемент (кроме элемента номер ноль) является суперфункцией для предыдущего элемента и передаточной функцией для последующего элемента. Физические приложения суперфункций, которые обосновывают термин «передаточная функция», предложены в работах [ 8 , 11 , 12 ]; суперфункция и ее обратная функция позволяют определять нецелые итерации функций и, в частности, такие экзотические функции, как ^ exp Кнезера [1 ] и V!, описанный в работе [ 11 ].

Способ аппроксимации решения уравнения ( 1 ) зависит от b . При 1 < b <  exp(1 / e) может использоваться так называемая регулярная итерация ( regular iteration ) [2, 3, 5–7, 9]. Для b >  exp(1 / e), решение можно вычислять через контурный интеграл [ 8] , предполагая, что эта функция голоморфна на множестве

C = C \{x G R : x <- 2 }. (5)

Такое представление позволяет выразить производную tet0 и вычислять обратную функцию, т. е. арктетрацию ate = tet-1. Для такой обратной функции может использоваться обозначение «суперлогарифм», slog, хотя tet-1 и не является суперфункцией от логарифма. Арктетрация удовлетворяет уравнению ate(exp(z)) = ate(z) + 1. (6)

Единственность решения ate, биголоморфного на множестве

G = {z G C : Re( z ) >  Re( L ); |z| < |L|}, (7)

исследуется в работах [ 8 , 10 ]. Здесь L ~ 0 . 318 + 1 . 337 i есть стационарная точка логарифма, т. е. решение уравнения L = log( L ). В языке программирования Maple константа L может быть представлена как conjugate(-LambertW(-1)) , а в языке Mathematica эта константа выражается как Conjugate[-ProductLog[-1]] .

В этой статье я предлагаю несложные аппроксимации функций tet и ate, которые могут быть прототипами для их численного complex <  double >  представления. Здесь я рассматриваю только случай b = e; log = ln = log _e и H = exp = exp _e . Тетрация при других значениях основания b >  e ^1/e может быть рассмотрена аналогичным образом. Ниже предлагается аппроксимация для функции tet = tet _e , показанная на рис. 1 толстой сплошной кривой, но эта аппроксимация не ограничивается вещественными значениями аргумента. Карты тетрации и арктетрации в комплексной плоскости показаны на рис. 2.

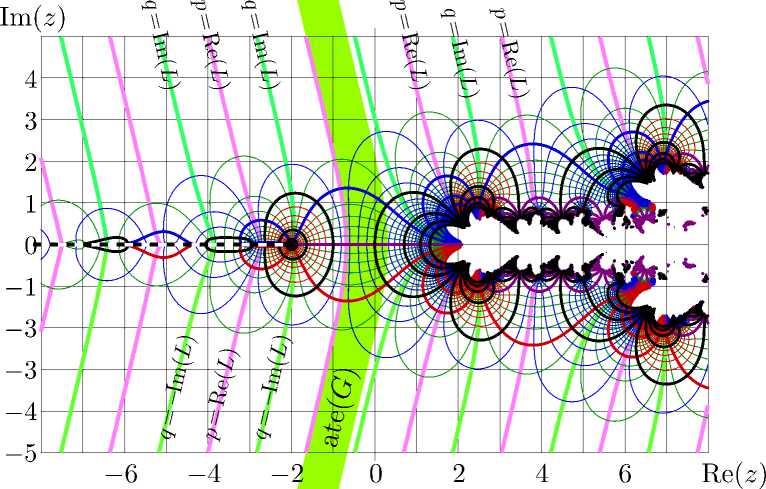
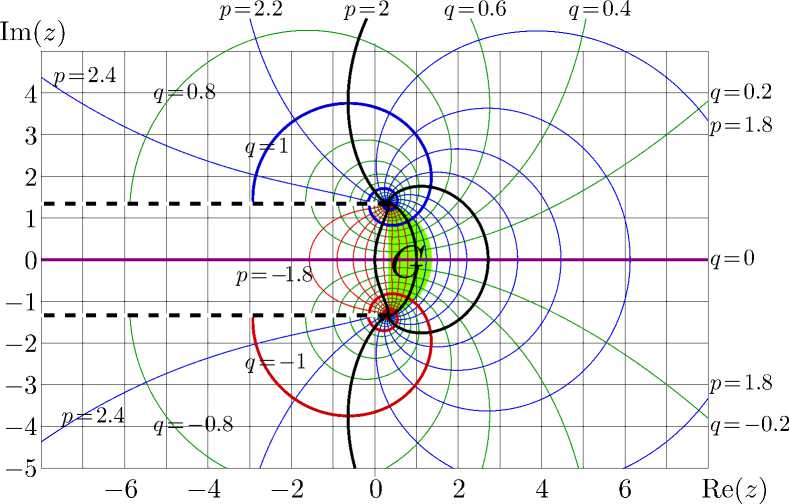
Рис. 2. Функции f = tet(z) и f = ate(z) в комплексной z-плоскости. Показаны уровни p = Re(f) = const и q = Im(f) = const.

• 2.    Свойства функций tet и ate

В этом параграфе обсуждаются свойства функций f = tet( z ) и f = ate( z ), следующие из их представления через контурный интеграл [ 8 ]. Поведение этих функций в комплексной плоскости z показано на рис. 2 с помощью линий p = Re( f ) = const и q = Im( f ) = const. Уровни целых значений p и q показаны толстыми темными линиями. Толстые светлые линии показывают уровни p = Re( L ) и |q| = Im( L ). Тонкие линии показывают промежуточные уровни, затененный серп — область G по формуле ( 7 ). Верхний угол этого серпа есть L , а нижний L ^∗ . Затененная полоса показывает домен ate( G ).

Функция tet имеет точку ветвления - 2 и разрез вдоль вещественной оси до -∞ . Положение этого разреза соответствует условию вещественности функции, т. е. tet( z ^∗ ) = tet( z ) ^∗ .

Функция ate имеет две точки ветвления, и необходимо выбрать положение линий разреза. В работе [ 8 ], линии разреза соответствуют уровню Re(ate( z )) = - 2, при этом разрезы «накручиваются» вокруг точек ветвления, и вычисление положений этих разрезов замедляет алгоритм вычисления арктетрации. Поэтому в этой работе линии разреза помещены вдоль прямых, параллельных вещественной оси.

Функция tet асимптотически приближается к своим предельным значениям L в верхней полуплоскости и L ^∗ в нижней полуплоскости. Это приближение видно на рис. 2 в той части, где линии p = Re( L ) почти параллельны линиям q = Im( L ). Стремление к значению L экспоненциальное [ 8] . Апроксимация тетрации tet( z ) при больших значениях Im( z ) должна использовать это свойство. В левой части комплексной плоскости, а также вблизи вещественной оси, кроме уравнения ( 1 ) функция f = tet удовлетворяет также «обратному» соотношению, т. е.

log^¡ f ( z +1)^¢ = f ( z ) ∀z ∈ C : | Im( f ( z )) | < π. (8)

Уравнения ( 1 ) и ( 8 ) упрощают аппроксимирование функций. Для численного представления тетрации, достаточно аппроксимировать эту функцию в некоторой связной области комплексной плоскости, которая простирается от - i ∞ до i ∞ так, что ширина ее сечения при каждом значении Im( z ) = const превышает единицу. Эта область может частично перекрываться с изображением tet( G ) домена G . В частности, этот район может быть полоской | Re( z ) | ≤ 1 / 2, использованной в работе [ 8 ], но может быть и «альтернативной полоской» - 1 ≤ Re( z ) ≤ 0, предложенной для проверки аппроксимации. Аналогично, для представления функции ate, достаточно аппроксимировать ее в некоторой области, которая простирается от L ^∗ до L так, что экспонента от левого края области попадает внутрь области (или хотя бы на правый край этой области).

Ниже, я предлагаю аппроксимации, построенные на основе дискретного представления этих функций через контурный интеграл [ 8 ]. Затем, свойства функций tet и ate используются для обобщения этих представлений на всю комплексную плоскость

• 3.    Численное представление тетрации: fima

Для того, чтобы отличать функции tet и ate от их аппрокимаций, я даю специальное имя каждой аппроксимации. Аппроксимации функции tet при больших значениях мнимой части аргумента получается из асимптотического разложения tet(z) = L + У^ Am,n exp (Lnz + amz). (9)

n,m

Подставляя такое разложение в уравнение ( 1 ) и считая exp( Lz ) малым параметром, получаю значение α = 2 π i и уравнения для коэффициентов A .

Учет нескольких слагаемых в разложении ( 9 ) дает асимптотическую аппроксимацию, назову ее fima:

N fima(z) =    anεn + βε exp(2πiz), n=0

где β является константой, малый параметр е = exp (Lz + R), а коэффициенты a0 = L≈ 0.3181315052047641353 + 1.3372357014306894089 i, a1 = 1, a2 = 1/2 ≈ -0.1513148971556517359 - 0.2967488367322413067 i,

L- 1

a 3 = ^{a 2 + 1/6} =     ^2+L ≈ - 0 . 03697630940906762 + 0 . 09873054431149697 i , (15)

L ² - 1    6( L - 1)( L ² - 1)

6+6 L +5 L ² + L ³

^{a 4 =} 24( L - 1) ³ ( L + 1)( L ² + L + 1)                         (16)

≈ 0 . 0258115979731401398 - 0 . 017386962126530755 i ,

24 + 36 L + 46 L ² + 40 L ³ + 24 L ⁴ + 9 L ⁵ + L ⁶

^{a 5 =} 120( L- 1) ⁴ ( L +1) ² (1+ L +2 L ² + L ³ + L ⁴ )                 (17)

≈ - 0 . 0079444196 + 0 . 00057925018 i .

Параметр R вводится для того, чтобы положить a1 = 1. Тогда получаются несложные выражения и других коэффициентов a через стационарные значение L логарифма. Значение этого параметра выбирается так, чтобы при фиксированном Re(z) и больших значениях Im(z) À 1 имела место асимптотика tet(z) = L + exp(Lz + R) + O (exp(2Lz)).                     (18)

Увеличение количества слагаемых в полиноме ( 10 ) и добавление полиномов от ε с множителями exp(2 π i z ), exp(4 π i z ), и т. д., улучшает аппроксимацию, но для алгоритма с 14-ю десятичными знаками, описанного ниже, достаточно в сумме ( 10 ) взять 6 слагаемых, полагая N = 5, и учесть одно слагаемое, пропорциональное exp(2 π i z ).

Я оцениваю параметры R и β , аппроксимируя численное решение [ 8 ]:

R ≈ 1 . 0779614375280 - 0 . 94654096394782 i ,                   (19)

β ≈ 0 . 12233176 - 0 . 02366108 i .                                (20)

Можно ожидать, что эти значения аппроксимируют фундаментальные математические константы. Приближение fima по формуле ( 10 ) показано на верхнем графике рис. 3 в тех же обозначениях, что и на рис. 2. В нижней части рис. 3 показано согласие

Im(z)

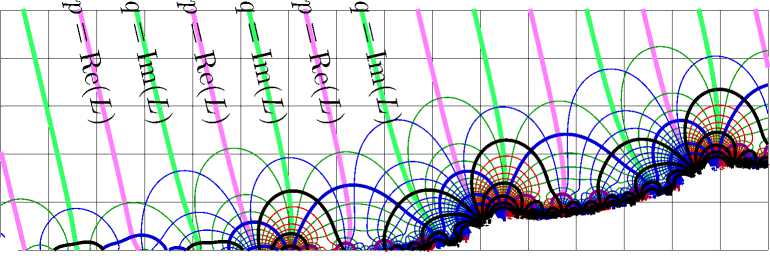
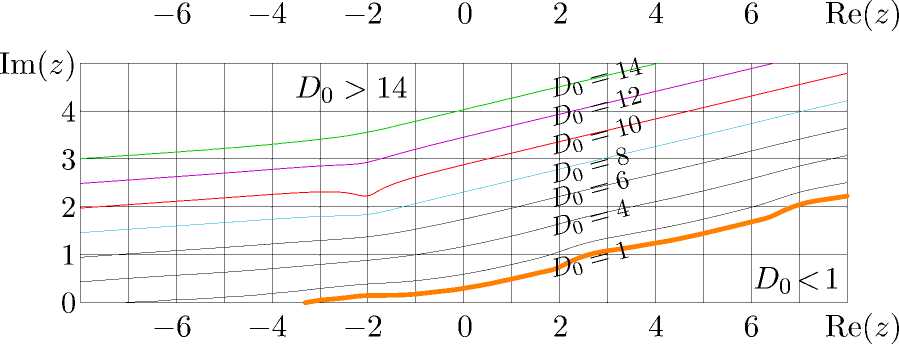
Рис. 3. Аппроксимация f = fima(z) по формуле ( 10 ) и согласие D o по формуле ( 21 )в комплексной z-плоскости.

Эта функция выражает невязку при подстановке F → fima в уравнение ( 1 ). Уровень D = 1 показан очень толстой светлой, самой нижней линией; уровни D = 2 , 4 , 6 , 8 — тонкими черными линиями; уровни D = 10 , 12 , 14 — толстыми линиями. Функция согласия указывает, сколько верных десятичных цифр можно ожидать получить в этом приближении. В частности, для значений аргумента над всеми проведенными линиями, можно ожидать получить по крайней мере 14 корректных десятичных знаков, в то время как для значений под нижней (самой толстой) линией, даже первый десятичный знак такого приближения сомнителен

Вместе с «сопряженным» приближением fima( z ^∗ ) ^∗ , аппроксимация ( 10 ) покрывает значительную часть комплексной плоскости, но не годится вблизи вещественной оси.

• 4.    Аппроксимация тетрации: разложение в нуле

Ряд Тэйлора имеет радиус сходимости, равный расстоянию от точки разложения до ближайшей сингулярности. В случае тетрации, конечная сумма ряда Маклорена дает приближение

N-1

naiv( z ) = ^X c _n z ⁿ , tet( z ) = naiv( z ) + O ( z ^N ) ,                     (22)

n=0

аппроксимирущее тетрацию при |z | <  2. Эта аппроксимация показана на рис. 4. Аппроксимации первых коэффициентов c _n представлены в первом столбце таблицы 1.

Таблица 1

Коэффициенты в разложениях ( 22 ) , ( 25 ) и ( 29 )

n	c n	s n	Re(t n )	Im(t n )
0	1.00000000000000	0.30685281944005	0.37090658903229	1.33682167078891
1	1.09176735125832	0.59176735125832	0.01830048268799	0.06961107694975
2	0.27148321290170	0.39648321290170	- 0.04222107960160	0.02429633404907
3	0.21245324817626	0.17078658150959	- 0.01585164381085	- 0.01478953595879
4	0.06954037613999	0.08516537613999	0.00264738081895	- 0.00657558130520
5	0.04429195209047	0.03804195209047	0.00182759574799	- 0.00025319516391
6	0.01473674209639	0.01734090876306	0.00036562994770	0.00028246515810
7	0.00866878181723	0.00755271038865	0.00002689538943	0.00014180498091
8	0.00279647939839	0.00328476064839	- 0.00003139436775	0.00003583704949
9	0.00161063129058	0.00139361740170	- 0.00001376358453	- 0.00000183512708
10	0.00048992723148	0.00058758348148	- 0.00000180290980	- 0.00000314787679
11	0.00028818107115	0.00024379186661	0.00000026398870	- 0.00000092613311
12	0.00008009461254	0.00010043966462	0.00000024961828	- 0.00000013664223
14	0.00001218379034	0.00001654344436	0.00000000637479	0.00000002270476
15	0.00000866553367	0.00000663102846	- 0.00000000341142	0.00000000512289
16	0.00000168778232	0.00000264145664	- 0.00000000162203	0.00000000031619
17	0.00000149325325	0.00000104446533	- 0.00000000038743	- 0.00000000027282
18	0.00000019876076	0.00000041068839	- 0.00000000001201	- 0.00000000013440
19	0.00000026086736	0.00000016048059	0.00000000002570	- 0.00000000002543
20	0.00000001470995	0.00000006239367	0.00000000000935	0.00000000000045
21	0.00000004683450	0.00000002412797	0.00000000000170	0.00000000000186
22	- 0.00000000154924	0.00000000928797	- 0.00000000000005	0.00000000000071
23	0.00000000874151	0.00000000355850	- 0.00000000000016	0.00000000000012
24	- 0.00000000112579	0.00000000135774	- 0.00000000000005	- 0.00000000000001
25	0.00000000170796	0.00000000051587	- 0.00000000000001	- 0.00000000000001

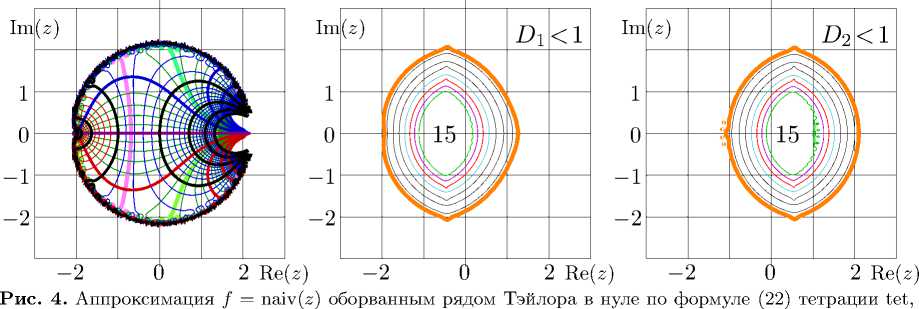
левый график; согласия D 1 и D 2 по формулам ( 23 ) и ( 24 ), центральный и правый графики.

Нулевой столбец таблицы 1 указывает номер n коэффициента, первый столбец — значение коэффициента c _n в формуле ( 22 ).

Точность аппроксимации ( 22 ) может быть охарактеризована функциями согласия:

D 1 = — 1g | exp(naiv( z — 1)) — naiv( z ) | ,

Эти функции построены на центральном и правом графиках рис. 4. Знак «15» указывает область, где согласие больше 14. Рисунок указывает, что при |z| ≤ 1, такая конечная сумма ряда Тэйлора дает порядка 15 значащих цифр.

Чтобы расширить область аппроксимации, имеет смысл «выключить» сингулярность в точке - 2, раскладывая функцию tet( z ) - log( z + 2) вместо функции tet( z ). Такое разложение дает приближение

N-1

maclo( z ) = log( z + 2) +     s _n z ⁿ ;

n=0

tet( z ) = maclo( z ) + O ( z ^N ) .

Название maclo (MAClaurin expansion with LOgarithm) указывает, что использованы разложение Маклорена и логарифм. Приближения коэффициентов разложения представ-

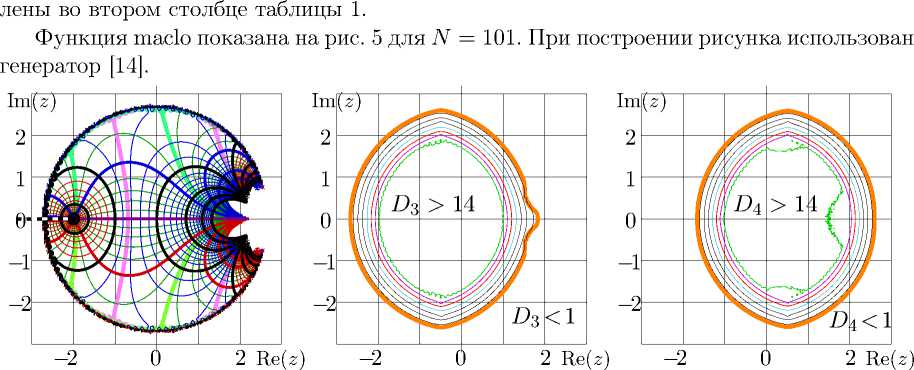
Рис. 5. Функция f = maclo(z) по формуле ( 25 ) при N = 101 в комплексной z-плоскости, слева; согласия

D 3 и D 4 по формулам ( 27 ) и ( 28 ), центр и справа.

Область аппроксимации тетрации функцией maclo шире, чем в случае непосредственного разложения тетрации в нуле. В правой части того же рис. 5 показаны согласия

D 3 = — lg I exp (maclo( z + 1)) — maclo( z )

D 4 = — lg I log (maclo( z — 1)) — maclo( z ) I .                         (28)

В центральной области невязки при подстановке tet → maclo в уравнения ( 1) , ( 8 ) имеют порядок величины 10 ^-15 .

• 5.    Разложение Тэйлора функции tet в точке 3i

Карты согласий D на рис. 3 и 5 указывают, что в области значений z ≈ 3i, каждая из аппроксимаций fima( z ) и maclo( z ) дает мало значащих цифр. В этой секции предложено разложение Тэйлора функции tet( z ) в точке z = 3i; назову такую аппроксимацию «tai» (TAylor expansion centered at the Imaginary axis):

N-1

tai( z ) = ^X t n (z — 3i) n .

n=0

Коэффициенты этого разложения оценены в последних двух столбцах таблицы 1.

Для N = 51 функция tai построена на рис

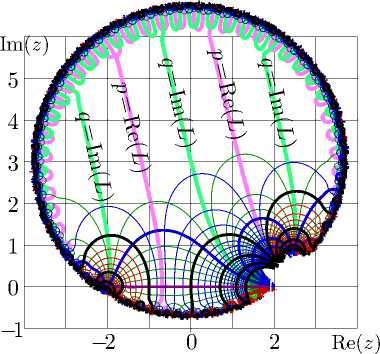
Рис. 6. Функция f = tai(z) по формуле ( 29 ) для N = 51 и согласие D 5 по формуле ( 30 ).

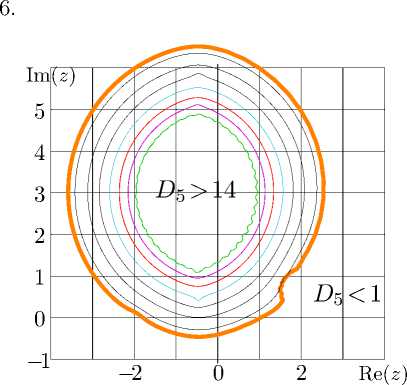
Рисунок построен с помощью генератора [ 15] . Погрешность аппроксимации решения уравнений ( 1 ), ( 8 ) характеризуется согласием

D 5 = - lg | log(tai( z + 1)) - tai( z ) |.

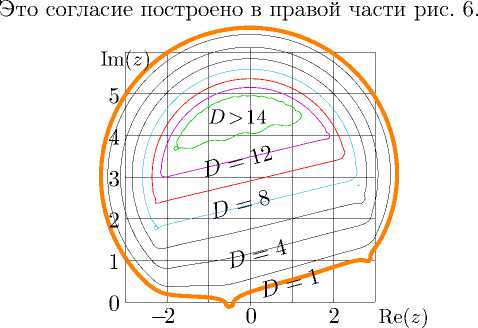
Рис. 7. Сравнение аппроксимации tai по формуле ( 29 ) с аппроксимациией fima по формуле ( 10 ), слева, и с аппроксимацией maclo по формуле ( 25 ), справа: согласия D = D 6 и D = D 7 по формулам ( 31 ), ( 32 ) в комплексной z-плоскости.

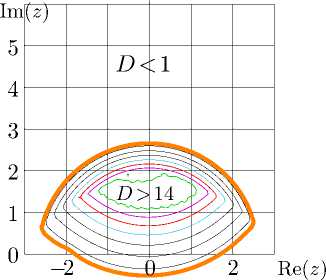
Взаимное согласие аппроксимаций может быть характеризовано функциями:

D 6 = - lg | fima( z ) - tai( z ) |,

D 7 = - lg | maclo( z ) - tai( z ) |.                                 (32)

Эти функции показаны на рис. 7. В центральных областях невязка не превышает 10 ^-14 . На основе этого рисунка я предлагаю следующую аппроксимацию:

fima( z ) ,

fse( z ) =

tai( z ) , maclo( z ) ,

tai( z * ) * , _ifima( z * ) * ,

4 . 5 <  Im( z ) ,

1 . 5 <  Im( z ) ≤ 4 . 5 ,

- 1 . 5 ≤ Im( z ) ≤ 1 . 5 ,

- 4 . 5 ≤ Im( z ) < - 1 . 5 , Im( z ) < - 4 . 5 .

Эту аппроксимацию интересно сравнить с результатами, опубликованными ранее. Ниже анализируется отклонение fse( z ) — F 4 ( z ), где F 4 ( z ) есть аппроксимация, полученная с помощью контурного интеграла [ 8] . В левой части рис. 8 показано согласие

D 8 = — lg | fse( z ) — F 4 ( z ) |

аппроксимации fse с аппроксимацией F 4 тетрации через контурный интеграл [ 8 ].

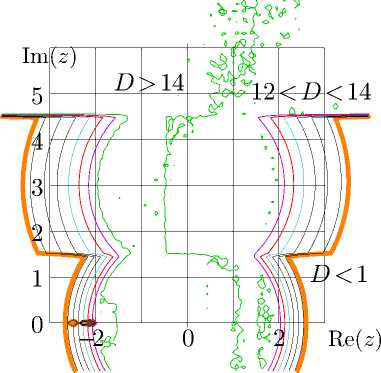
Рис. 8. Согласие D = D 8 по формуле ( 34 ), слева; аналогичное согласие для контурного интеграла со сдвинутой на -0.5 базовой областью, справа.

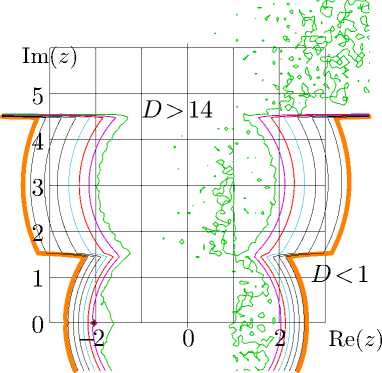
Рис. 8 выявляет дефекты каждой из аппроксимаций. Скачки при Im( z ) = 1 . 5 и при Im( z ) = 2 . 5 вызваны переходом от функции maclo к функции tai и от функции tai к функции fima в комбинации FSE. Скачки при полуцелых значениях Re( z ) вызваны разрывами функции F 4 , которая расширяет начальное приближение, справедливое для | Re( z ) | <  1, используя | Re( z ) | <  1 / 2 в качестве базового интервала. Ошибки округления приводят к нерегулярной структуре. По крайней мере внутри полоски | Re( z ) | <  1 . 5 взаимные отклонения этих аппроксимаций имеют порядок величины 10 ^-14 .

В правой части рис. 8 построено согласие для функции F 5 , которая аналогична функции F 4 , но базовый интервал сдвинут на — 1 / 2. Аппроксимация F 5 имеет скачки при целых значениях вещественной части. Эти скачки тоже малы; согласие во всяком случае не хуже, чем для функции F 4 .

Таким образом, различие всех трех аппроксимаций имеет порядок величины 10 ^-14 . На основе рис. 7, 8 я предлагаю финальную аппрокцимацию FSE (Fast Super Exponential) тетрации tet:

' FIMA( z ) ,

	TAI( z ) ,
FSE( z ) = <	MACLO( z ) ,

TAI( z * ) * ,

_FIMA( z * ) * ,

4 . 5 <  Im( z ) ,

1 . 5 <  Im( z ) <  4 . 5 ,

— 1 . 5 <  Im( z ) <  1 . 5 , — 4 . 5 <  Im( z ) < — 1 . 5 , Im( z ) < — 4 . 5 ,

где

FIMA( z ) =

{fima(z), exp(FIMA(z - 1)),

Im( z ) >  4 + 0 . 2379Re( z ) ,

Im( z ) <  4 + 0 . 2379Re( z ) ,

tai( z ) ,

TAI( z ) = log(TAI( z + 1)) ,

_exp(TAI( z - 1)) ,

| Re( z ) | <  0 . 5 ,

Re( z ) < - 0 . 5 ,

Re( z ) >  0 . 5 ,

tai( z ) ,

MACLO( z ) = log(MACLO( z + 1)) ,

^exp(MACLO( z - 1)) ,

| Re( z ) | <  0 . 5 , Re( z ) < - 0 . 5 , Re( z ) >  0 . 5 .

Эта аппрокцимация дает по меньшей мере 14 верных десятичных знаков голоморфной тетрации tet и согласуется с результатами [ 8 ].

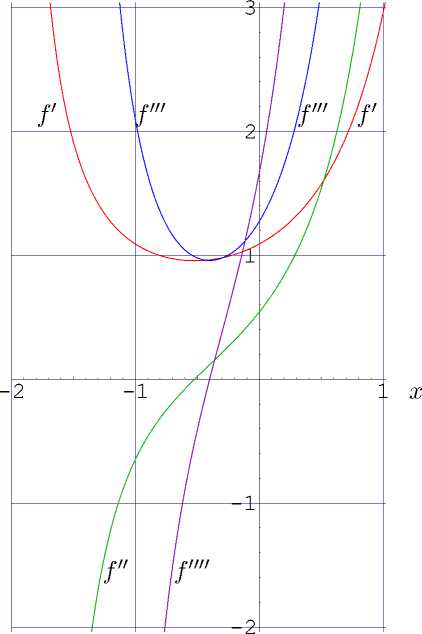
Рис. 9. Первые четыре производные функции f = tet(x) для вещественных значений х.

Насколько я могу судить, эта аппроксимация быстрее и точнее всех аппрокцимаций голоморфной тетрации, публиковавшихся ранее. Большое число слагаемых сохранено в аппроксимациях ( 29 ) и ( 25 ) для того, чтобы обеспечить их хорошее перекрытие на рис. 7 и 8. На конечной стадии имплементации количество слагаемых в аппроксимациях рядов может быть уменьшено без потери точности. Особенно это относится к вычислению тет-рации на вещественной оси: достаточно обеспечить хорошую аппроксимацию функции tet( z ) для |z| <  1 / 2, что составляет всего четвертую часть от радиуса круга, в котором аппроксимация тетрации функцией maclo дает 14 знаков.

По просьбе коллег, я перевел алгоритм быстрого вычисления тетрации и арктетрации с языка С++ на язык Mathematica. В качестве примера использования, на рис. 9 с этим алгоритмом построены первая, вторая, третья и четвертая производные тетрации, как функции вещественного аргумента. Код, генерирующий этот рисунок, доступен на ситизендиуме [ 16 ]. В принципе, с тем же кодом (т. е. на языке Mathematica) можно получать и другие рисунки для тетрации и арктетрации по основанию e и, в частности, карты этих функций в комплексной плоскости.

• 6.    Аппроксимация арктетрации ate , функция FSL

Обратная функция тетрации, т. е. арктетрация ate = tet ^-1 , удовлетворяет уравнениям:

ate( z ) = ate(exp( z )) - 1 ,

ate(z) = ate(log(z)) + 1, по крайней мере, пока z ∈ G. Кроме того, ate(1) = 0. Эта функция может быть представлена как численное решение уравнения tet(ate(z)) = z; однако, такое представление существенно медленнее, чем аппроксимация с помощью подходящих элементарных функций.

Первая (и наивная) попытка численного представления функции ate — это, естественно, разложение Тэйлора в единице. Коэффициенты такого разложения можно найти, обращая ряд naiv по формуле (22). Радиус сходимости такого обращенного ряда есть |L| ≈ 1.5, причем аппроксимация особенно плоха в окрестности стационарных точек L и L∗ логарифма. Лучше разложить функцию ate(z) - log(zL- L)

-

log( z - L ^∗ ) L ^∗

в точке z = 1. Такое разложение ведет к аппроксимации fsl(z)=log(zL-L)+log(zL-∗L∗)+NX1un(z-1)n; n=0

ate( z ) = fsl( z ) + O ^¡( z - 1) ^{N ¢}

Приближенные значения первых коэффициентов u этого разложения представлены в таблице 2. Аппроксимация fsl при N = 70 показана на рис. 10.

Формально, разложение Тэйлора функции ( 41 ) в точке z = 1 имеет тот же радиус сходимости, что и разложение Тэйлора функции ate. Однако практически, при численном представлении функции, аппроксимация по формуле ( 42 ) сходится существенно быстрее, чем непосредственное разложение Тэйлора функции ate. Функция fsl аппроксимирует ate даже на границе круга сходимости ряда и, в частности, вблизи концов серпа G , т. е. вблизи точек L и L ^∗ . Функция fsl имеет те же точки ветвления L и L ^∗ , что и функция ate, и тоже принимает бесконечные значения в этих точках.

Таблица 2

Коэффициенты u n в разложении ( 42 )

n	u n	n	u n	n	u n
0	1 . 41922521550451	10	0 . 00000003111805	20	0 . 00000000002293
1	- 0 . 02606629029752	11	0 . 00000002940887	21	- 0 . 00000000002462
2	0 . 00173304781808	12	- 0 . 00000001896929	22	0 . 00000000000666
3	- 0 . 00001952130725	13	0 . 00000000351784	23	0 . 00000000000322
4	- 0 . 00006307006450	14	0 . 00000000204270	24	- 0 . 00000000000354
5	0 . 00002567895998	15	- 0 . 00000000171995	25	0 . 00000000000096
6	- 0 . 00000559010027	16	0 . 00000000039882	26	0 . 00000000000051
7	- 0 . 00000007279712	17	0 . 00000000019328	27	- 0 . 00000000000055
8	0 . 00000065148872	18	- 0 . 00000000019113	28	0 . 00000000000014
9	- 0 . 00000027698138	19	0 . 00000000004947	29	0 . 00000000000009

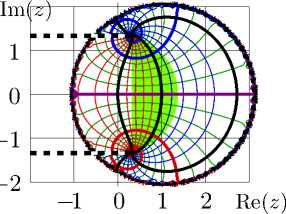
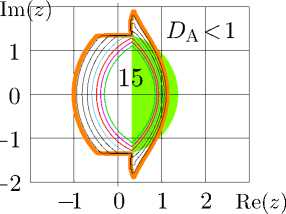
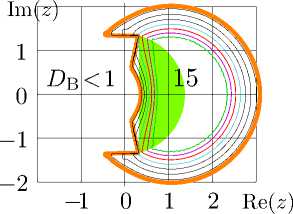
Рис. 10. Функция fsl(z) по формуле ( 42 ), слева; согласия по формулам ( 44 ) и ( 45 ), центр и справа; область G по формуле ( 7 ) затенена.

Чтобы оценить невязки при подстановке ate → fsl в уравнения ( 39 ), ( 40 ) согласия

D a = - lg | fsl ( exp( z )⁾ - 1 - fsl( z ) I ,                               (44)

D b = - lg | fsl ( log( z ) ) + 1 - fsl( z ) |

построены на центральном и правом графиках рис. 10. Как и раньше, символ «15» указывает область, где согласие лучше четырнадцати. (Внутри внутренних контуров, невязки не превышают 10 ^-14 .)

Область аппроксимации может быть расширена с помощью функции fsl(z),

FSE( z ) =

FSL(exp( z )) - 1 ,

FSL(log( z )) + 1 ,

| Im( z ) | <  Im( L ) & ,

|z- 1 | ≤ | log( z ) - 1 | &  |z- 1 | ≤ | exp( z ) - 1 |,

| Im( z ) | <  Im( L ) &  |z- 1 | > | exp( z ) - 1 |,

| Im( z ) | ≥ Im( L ) or |z- 1 | > | log( z ) - 1 |.

Расширение ( 46 ) позволяет накрыть всю комплексную плоскость с помощью одной единственной аппроксимации элементарной функцией ( 42 ). Чтобы проверить взаимное соответствие аппроксимаций FSE и FSL, рассмотрим согласия:

D c = - lg|FSL ( FSE( z ) ) - z | , D d = - lg | FSE ( FSL( z ) ) - z I .

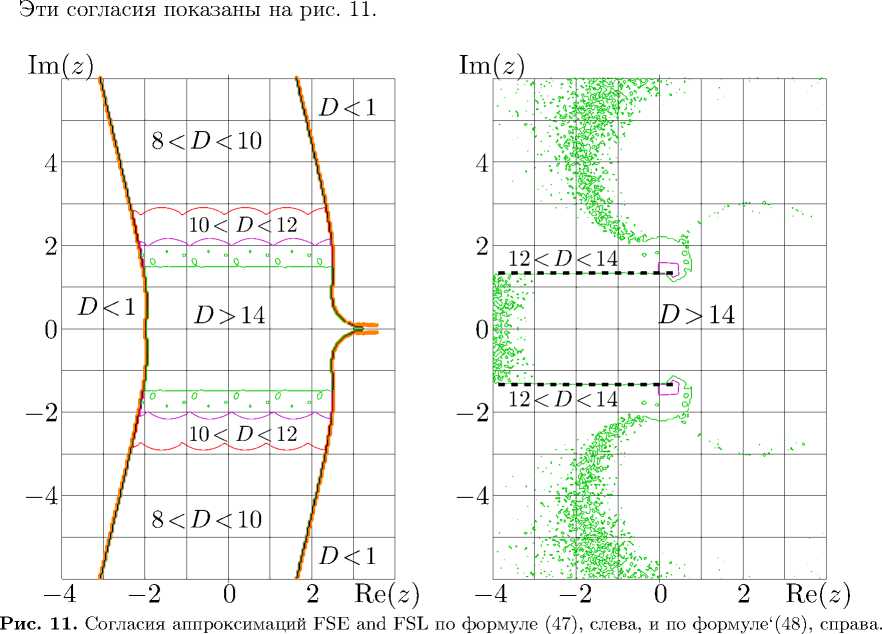
Рисунок подтверждает хорошую точность аппроксимации; ее погрешность сравнима с ошибками округления при использовании переменных complex h double i .

Заключение

Разработан численный алгоритм FSE по формуле ( 35 ) для вычисления голоморфной тетрации (суперэкспоненты) по основанию e. Предложен также алгоритм FSL по формуле ( 46 ) для вычисления обратной функции. Пока эти алгоритмы самые точные и самые быстрые; они могут быть прототипами для численной реализации тетрации и арктетрации в компиляторах следующего поколения.