The Analysis and Investigation of Multiplicative Inverse Searching Methods in the Ring of Integers Modulo M
Автор: Zhengbing Hu, I. A. Dychka, Onai Mykola, Bartkoviak Andrii
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 11 vol.8, 2016 года.
Бесплатный доступ
In this article an investigation into search operations for the multiplicative inverse in the ring of integers modulo m for Error Control Coding tasks and for data security is shown. The classification of the searching operation of the multiplicative inverse in the ring of integers modulo m is provided. The best values of parameters for Joye-Paillier method and Lehmer algorithm were also found. The improved Bradley modification for the extended Euclidean algorithm is also offered, which gives the operating speed improvement for 10-15%. The integrated experimental research of basic classes of searching methods for multiplicative inverse in the ring of integers modulo m is conducted for the first time and the analytical formulas for these calculations of random access memory necessary space when operated at k-ary RS-algorithms and their modifications are shown.
Integers modulo m, Error control coding, Data security, Euclidean algorithm
Короткий адрес: https://sciup.org/15010871
IDR: 15010871
Текст научной статьи The Analysis and Investigation of Multiplicative Inverse Searching Methods in the Ring of Integers Modulo M
Published Online November 2016 in MECS
Modular arithmetic is basic when realizing the majority of cryptographic algorithms, public-key algorithms in particular. One of the most computationally intensive operations of modular arithmetic is searching for multiplicative inverse in the ring of residues modulo m , where m > 2 and m is integer. This operation is used in multiplying the point of elliptic curve by the number in affine coordinates over the finite field GF ( p ), in Diffie-
Hellman the key exchange method, RSA algorithm and many other algorithms which realize public-key cryptography methods [1-3]. Furthermore, while Error Control Coding of data and in some algorithms of pseudorandom-number generation the necessity of multiplicative inverse searching also arises [4, 5]. That is why the task of searching and investigating the effective methods of finding the multiplicative inverse in the ring of residues modulo m by minimalistic criterion of computational and time complexity is topical.
-
II. C LASSIFICATION OF S EARCHING M ETHODS OF M ULTIPLICATIVE I NVERSE IN THE R ING OF R ESIDUES M ODULO M
The multiplicative inverse for the integer b in modular arithmetic is such an integer y , for which the following equation is attained:
b • y = 1 ( mod m ) .
The condition for multiplicative inverse existing is when GCD ( b ; m ) = 1. If this condition is not met, then the multiplicative inverse modulo m for the integer b does not exist [4, 6-8].
The searching methods of multiplicative inverse can be divided into two classes: methods which are derived from greatest common divisor searching methods and methods which are based on modular exponentiation (figure 1).
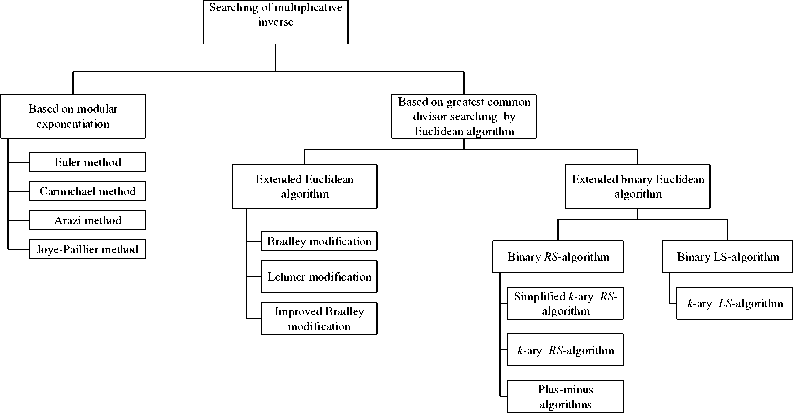
Fig.1. Classification of searching methods of multiplicative inverse
-
III. S EARCHING M ETHODS OF M ULTIPLICATIVE I NVERSE B ASED ON M ODULAR E XPONENTIATION
-
A. Euler, Carmichael and Arazi Methods
According to Euler theorem, if GCD ( b; m ) = 1, than:
Ьф (m) = 1 ( mod m ), where ф(m) — Euler function.
If we multiply the equation (1) by b 1 we will get:
b—1 = ЬФ (m)—1 ( mod m ).
At the same time, according to Carmichael function definition [9] for any b , which satisfies the condition GCD ( m ; b ) = 1 , the following equation holds true:
b^ m ) = 1(mOd m ), where Я(m)- Carmichael function.
From the equation (3) we will get the searching method of multiplicative inverse in the ring of residues modulo m , based on Carmichael function (we will name it Carmichael method):
b — 1 = b^-m ) - 1 ( mod m ) .
So, to find multiplicative inverse we need to find the value of the Euler function ф ( m ) or Carmichael function Я ( m ) and to do the modular exponentiation.
If modulo m is a prime number, than ф ( m ) = Я ( m ) = m - 1 and b 1 = bm — 2 ( mod m ) .
In case when multiplicative inverse to m modulo b is to be found easier than multiplicative inverse to b modulo m , the Arazi formula is used [10, 11]:
b 1 ( mod m ) =
1 + m ■ ( - m 1 mod b
When b is a prime number, the Arazi formula is simplified in the following way:
b 1 ( mod m ) =
1 + m ■ ( - m b 2 mod b )
b
If b and m are composite numbers and the condition
GCD ( m ; b ) = 1, is met for them, then for b — 1 ( mod m ) finding we can use the following formula:
1 + m ■ ( - m ^ b ) 1 mod b ) b ( mod m ) =--------------------- , (4)
which allows to find b 1 ( mod m ) , faster than formula (3), because the value Я ( b ) is calculated easier than Я ( m ) due to b < m . This method of multiplicative inverse searching will be named the Arazi method.
-
B. Joye-Paillier Method
If m and b are composite numbers, then while searching b — 1 ( mod m ) the necessity of calculating of Euler or Carmichael function appears. To avoid it Joye and Paillier offered [11] to find b ' = b + Cm , where C — arbitrary integer constant, and b — prime number.
Obvious is the fact that b 1 ( mod m ) = ( b') 1 ( mod m ), that’s why the transition from argument b to argument b' allows to avoid the evaluation of Euler or Carmichael function.
The searching of the necessary constant C can be done in a number of ways. For the purpose of investigation, we are to analyze four algorithms when searching the values of constant С , where the easiest algorithm is to scan all the values of С beginning with 1 until b ' is prime number (we will name such an approach to realize the Joye-Paillier method an algorithm №0).
Another approach for choosing the constant C lies in the fact that initial value of constant С is taken to be equal to [ 1 - ь л ( T ) J mod t , where T is the product of definite set of prime numbers, and then the value of b ' increases on value of m • T until we get prime b '. We will name such an approach to realize the Joye-Paillier method an algorithm №1.
We can expect the operating speed improving if we trace modulo m to prime number m by adding the value proportional to b • T and do the calculation according to the following formulas:
u = bm - 2 ( mod m ' ) ,
-
- 1/ 1 + b • ( m '- u )
v = m (mod b ) =------------, m'
-
- I 1 + m • ( b - v )
b 1 ( mod m ) =------.
Formulas (5) and (6) can be combined into one:
z m ' + m ( b • u -1 )
b (mod m) =--------------
-
V ’ b • m'
We will name such a realization of the Joye-Paillier method an algorithm №2.
If modulo m is a very big number comparing to argument b , then it is suitable to do the reduction m ' = m ( mod b ) with further bringing m' to prime number by increasing on the value which is proportional to b • T and do the calculation according to the following formulas:
u = bm-2 (mod m'), m • u - m + C b (mod m) =-----^-^.
We will name such an approach to realize the Joye-Paillier method an algorithm №3.
Instead of integer division, it is recommend to perform all the operations modulo 21 m, where |m| - bit length of number m. While performing the operations modulo 2m the integer division boils down to division modulo 2 m , which is quickly performed with the help of Newton’s method.
-
IV. S EARCHING M ETHODS OF M ULTIPLICATIVE I NVERSE B ASED ON S EARCHING T HE GCD
It is proved that from the computational viewpoint the most effective methods of searching the GCD are the methods based on Euclidean algorithm [4, 6].
The idea of searching the GCD can be adapted to the needs for finding the multiplicative inverse. The extended Euclidean algorithm is used for it, which allows finding the GCD of two numbers m and b and such coefficients x and y the following equation to hold true [4, 6-7]:
x • m + y • b = d , (7)
where d – is the greatest common divisor for m and b .
If we perform the equation (7) modulo m , that we will get:
y • b = d ( mod m ) .
For the case d = 1 we can see that element y is multiplicative inverse to b modulo m . At the same time GCD ( b ; m ) = 1 is the necessary condition for existing of the multiplicative inverse. So, we can draw the conclusion: if the multiplicative inverse exists, it can be always found with the help of extended Euclidean algorithm for GCD search.
When developing the extended Euclidean algorithm for GCD search it is necessary to keep the performance of two equations:
u = A • m + B • b ; (8)
v = C • m + D • b , (9)
Furthermore, at the beginning of algorithm u = m , v = b .
To provide the execution of equations (8) and (9) you need to define A = 1, B = 0, C = 0, D = 1 at the beginning of algorithm. The values u and v in the process of the algorithm change in the same way as in the process of the Euclidean algorithm for searching the greatest common divisor. The value of A , B , C and D changes to exactly maintain the execution of equations (8) and (9).
The methods based on searching the greatest common divisor can be divided into two subclasses:
-
1) methods based on Euclidean algorithm;
-
2) methods based on binary Euclidean algorithm.
-
A. The Extended Euclidean Algorithm and Its Modifications
The first subclass (figure 1) of the extended algorithms is the extended Euclidean algorithms, which main ideas were established in India in the 5th century [3].
These algorithms are based on the following identity GCD ( m;b ) = GCD ( b ; m mod b ) and in the process of the algorithms the execution of equations like (8) and (9) are maintained.
It was shown by Gordon Bradley [4, 6], that it is enough to maintain the equations like:
A • m = u and C • m = v, and in the end to find the value of the second coefficient using the formula в = u - A'm .
b
It is obvious that to find b - 1 ( mod m ) there is no need to search both coefficients of the equation (8), it is enough to find the coefficient of b . Considering this fact and using Bradley idea we offered to modify the extended Euclidean algorithm in such a way that it will find only coefficient B , i.e. in the process of performing the algorithm will maintain only in equations like B • b = u and D • b = v . Beside this, it is offered that the stopping of the iterative process to be performed by the value v = 1, not v = 0, like in the basic algorithm. We will name such an algorithm the improved the Bradley modification of the extended Euclidean algorithm.
The modification of the Euclidean algorithm for searching the GCD of two numbers with big bitness [4] was offered by French scholar Lehmer. His idea lies in m the fact that for big numbers the fraction won’t
b change if in numbers m and b we divest the certain amount of junior bits. Using this idea, we can build the extended Lehmer algorithm. The drawback to this algorithm is the fixed amount of junior bits which is divested while operands can have different length. That’s why efficient is to find the optimal amount of bits divested for operands’ length given.
-
B. The Extended Binary Euclidean Algorithm and Its Modifications
The second subclass (figure 1) of the extended algorithms is the extended binary Euclidean algorithms.
These algorithms in the process of performing also maintain the execution of equations (8) and (9), but on every iteration the division on two of following equations takes place hence comes the name of this subclass of algorithms. Herewith on every iteration in the checking of A and B coefficients on parity takes place. If both coefficients are binary the division on two takes place, if not – than b is added to A , and m is subtracted from B . So, the binary numbers are received which then are divided on 2 again.
It can be proved that in case m is odd and b is binary and the condition A and B are binary is not true – all that will always evidence that A is binary and B is odd. For the case when m and b are odd, the parity of A and B coincides. So, it is enough to check for parity only B .
So, for the odd modulus it is enough to maintain only the equation like B • b = u . If the modulus is binary, then for the correct performing of the algorithm it is enough to maintain the equation like A • m = u , and the value of B it is possible to find using the formula в = u - A ' m .
b
So, at the beginning of the process of the binary algorithm it is necessary to check the modulus parity and then to maintain equations like A • m = u or B • b = u . Only owing to it, it is possible to reduce the amount of operations almost doubly.
There are two fundamental approaches to building the algorithms which realize binary methods: Right-Shift (RS) and Left-Shift (LS) .
The first approach (RS) is based on the following identities:
-
1) if u and v are binary, then
GCD ( u ; v ) = 2 • GCD | u ; - | ;
v 7 (2 2J
-
2) if u is binary, and v is odd, then
GCD ( u ; v ) = GCD f u ; v ^ ;
-
3) if u and v are odd, then
f | u - v| )
GCD ( u ; v ) = GCD I ; v I ;
-
4) if v = 0 , then
GCD ( u ; 0 ) = u .
According to binary RS -Euclidean algorithm when searching the GCD of two numbers the values of arguments are reduced by dividing by 2, which is the equivalent of indentation on one binary digit bit.
The generalization of the binary algorithm is k -аry algorithm. When building such an algorithm comparing to binary the term “pairity” is replaced by “co-prime with k ” and during the realization of iteration process division by k is done.
The second approach (LS) is based on the following identities:
-
1) GCD ( u ; v ) = GCD (| u + 1 • v |; v ) , where t – is any
integer;
-
2) GCD ( u ;0 ) = u .
According to this approach the number t is calculated minus and such that is power of two, then the value of t ■ v can be found by out dent of v on certain amount of binary digit bits. For k -ary algorithm t is chosen like the power of the number k .
So, there arises the necessity of investigation of the influence of the value of k on the effectiveness of k -ary searching method of multiplicative inverse in the ring of residues modulo m .
At the same time there are two known [13] modifications for the binary RS -algorithm, which positioned the algorithms for hardware implementation. The peculiarity of these algorithms is that they on every iteration operate only with two least significant bits of operands. These algorithms are called extended plusminus algorithms.
-
V. T HE E XPERIMENTAL R ESEARCH
For the experimental investigation into the software product on computer programming language C# was designed in Visual Studio 2013 framework. The experimental research was carried out on the computer with the following technical characteristics: CPU Intel Core I5-3210М, 2.5 GHz, random access memory 8 Gb.
The software product allows testing the correctness of the process of the algorithms, generating incoming data with set characteristics and receiving the timing data of the processes of algorithms at specified arguments.
-
А. The Research of Euler, Carmichael and Arazi Methods
In the designed software product Euler method, Carmichael method and two modifications of Arazi method are realized, the Arazi method using Euler formula and the Arazi method using Carmichael formula in particular (figure 1).
To carry out the research of the algorithm operating speed four sets with pairs of random numbers m and b were formed. Every set of numbers contains 50 odd modules m of certain length (8, 16, 20, 32 bits) and 100 numbers b for every m .
In table 1 an average performing time of every method for one pair m and b is given. From received results one can see that the best time indexes as Arazi method based on Euler formula. At the same time Carmichael method and Arazi method based on Carmichael formula for modules with length of 32 bits do not give result in acceptable time.
Table 1. The Execution Time of Algorithms Based on Modular Exponentiation, ms
|
Method name |
The length of the module, bit |
|||
|
8 |
16 |
20 |
32 |
|
|
Euler method |
0,1 |
3,0 |
50,2 |
201732,9 |
|
Carmichael method |
4,8 |
378,5 |
7047,7 |
– |
|
Arazi method (based on Euler formula) |
0,1 |
0,9 |
16,3 |
9131,7 |
|
Arazi method (based on Carmichael formula) |
1,0 |
822,0 |
77260,2 |
– |
-
В. The Research of Joye-Paillier Method
For the Joye-Paillier method analysis (figure 1) the four algorithms of realization of this method were designed.
For the purpose of the research in the performance of Joye-Paillier method in for searching of multiplicative inverse the two classes of number sets with pairs of random numbers m and b were formed, each of them containing four sets with different length of the module (128, 256, 512, 1024 bit). To the first class sets containing m which are prime numbers belong, to the second class – sets containing odd m which have for at least 5 prime divisors. Every set consists of 50 modules m with specified characteristics and fixed length, and also
100 such numbers b for every m so that the condition GCD ( m; d ) = 1 is satisfied.
In the algorithms №1, №2 and №3 the parameter T is used which is the multiplication of certain set of prime numbers. About the choice of values of this parameter there are no recommendations in the article [11] that’s why we searched for optimal set of multipliers for T by looking through the multiplications of all the prime numbers from 2 to 23 (tables 2-3).
For optimal values of parameter Т the results with involvement of arithmetic modulo 2 are given in tables 4 and 5.
Table 2. Optimal Values of Parameter T for Prime Modules
|
The number of algorithm |
The length of the module, bit |
||||
|
128 |
256 |
512 |
1024 |
||
|
№0 |
Time, ms |
4,7 |
22,0 |
254,4 |
5087,9 |
|
№1 |
Time, ms |
3,0 |
8,1 |
52,6 |
135,1 |
|
Multipliers T |
{3;5;7;11;13} |
{2;7;17;19} |
{3;13;17;19} |
{2;3;13;17;23} |
|
|
№2 |
Time, ms |
1,9 |
6,2 |
47,3 |
174,5 |
|
Multipliers T |
{2} |
{2;3;5;7;13;19} |
{3;13} |
{7;11} |
|
|
№3 |
Time, ms |
2,0 |
7,1 |
51,5 |
196,8 |
|
Multipliers T |
{2} |
{2;3;5;7;13;19} |
{3;13} |
{7;11} |
|
Table 3. Optimal Values of Parameter T for Composite Modules
|
The number of algorithm |
The length of the module, bit |
||||
|
128 |
256 |
512 |
1024 |
||
|
№0 |
Time, ms |
4,0 |
25,8 |
551,8 |
6285,5 |
|
№1 |
Time, ms |
2,4 |
9,2 |
41,7 |
145,7 |
|
Multipliers T |
{3;5;7;11;13;19} |
{2;3;11;13;17;23} |
{2;3;5;13;17} |
{2;3;5;7;11;13;17;19} |
|
|
№2 |
Time, ms |
2,0 |
6,3 |
57,5 |
184,7 |
|
Multipliers T |
{2;5;11;13;17;23} |
{2;3;5;7;11;13;23} |
{2;3;5;7;17} |
{3;5} |
|
|
№3 |
Time, ms |
2,2 |
7,3 |
57,6 |
185,3 |
|
Multipliers T |
{2;5;11;13;17;23} |
{2;3;5;7;11;13;23} |
{5;7;11} |
{5;7;11;13;17;19;23} |
|
From the received experimental results, it is evident for every fixed length of operands there exists its own set of optimal values of range of multipliers for parameter T. Among the four algorithms were investigated, the best results for module with length of 512 bits shows algorithm №2, and for the module with length of 1024 bits almost on 25% algorithm №1 is better. Such a tendency retains for both prime and composite modules.
Table 4. Operating Time of Algorithms which realize Joye-Paillier Method for Prime Modules with Involvement of Arithmetic Modulo 2, ms
|
The number of algorithm |
The length of the module, bit |
|||
|
128 |
256 |
512 |
1024 |
|
|
№0 |
4,6 |
20,9 |
250,4 |
7375,3 |
|
№1 |
2,8 |
7,1 |
51,2 |
126,4 |
|
№2 |
1,9 |
6,2 |
48,6 |
172,8 |
|
№3 |
1,9 |
5,8 |
46,9 |
178,7 |
Table 5. Operating Time of Algorithms which realize Joye-Paillier Method for Composite Modules with Involvement of Arithmetic Modulo 2, ms
|
The number of algorithm |
The length of the module, bit |
|||
|
128 |
256 |
512 |
1024 |
|
|
№0 |
3,8 |
24,7 |
587,9 |
6507 |
|
№1 |
2,3 |
9,3 |
46,9 |
139,1 |
|
№2 |
2,1 |
6,5 |
56,8 |
177,2 |
|
№3 |
2,1 |
7,2 |
54,3 |
185,8 |
Table 6. The Operating Time of Algorithms of Searching the Multiplicative Inverse
|
Name of method |
The length of the module, bit |
||||||
|
128 |
256 |
512 |
1024 |
2048 |
4096 |
8192 |
|
|
Extended Euclidean algorithm |
0,06 |
0,14 |
0,31 |
0,72 |
1,96 |
5,62 |
19,16 |
|
Improved Bradley modification of extended Euclidean algorithm |
0,04 |
0,10 |
0,22 |
0,55 |
1,51 |
4,33 |
15,08 |
|
Plus-minus algorithm №1 |
0,36 |
0,85 |
2,24 |
6,58 |
21,54 |
74,86 |
291,77 |
|
Plus-minus algorithm №2 |
0,33 |
0,81 |
2,27 |
6,57 |
22,04 |
78,26 |
306,21 |
In the tables 4 and 5 the operating time of algorithms which realize Joye-Paillier method by optimal sets of multipliers of parameter T with involvement of arithmetic modulo 2. From the given tables we can see that involvement of arithmetic modulo 2 instead of integer division for all the algorithms gives small increase of performance.
-
С. The Research of Methods based on Euclidean Algorithm
With the purpose of research into the operating speed of this class of algorithms based on searching GCD (greatest common divisor) of two numbers with the help of Euclidean algorithm (figure 1), formed seven sets with pairs of random numbers m and b . Every set contains 50 odd modules m with fixed length (128, 256, 512, 1024, 2048, 4096, 8192 bits) and 100 numbers b for which there exists multiplicative inverse modulo m .
The experimental results for extended Euclidean algorithm, improved Bradley modification of extended Euclidean algorithm and two plus-minus algorithms are given in table 6.
Within the survey RS - and LS - realization of k -ary extended algorithm for arbitrary k were built. Besides, the simplified extended k -ary RS -algorithm was realized, which works only for values of k that are the power of prime number. It allows to essentially simplify the procedure of finding the coefficient х by which the equations A — X • V and B + X • U are aliquot to k . To k -ary LS- algorithm such modification is not efficient, because according to this algorithm the value of multiplier is chosen like a power of k not depending on a value of k .
To determine the optimal value of k the research of realized algorithms on three sets of values of k was conducted, namely the value of k, which is the power of 2 (the index of power changed from 1 to 22), the value of k, which is the power of 3 (the index of power changed from 1 to 14) and the arbitrary k. In the tables there are no time indexes of performing of LS-algorithm, because during the acceptable time it is possible to get the result only for values k < 1024 and these results considerably lose on time indexes to RS-algorithms. Besides, LS-algorithms are characterized of considerable using the memory, because the amount of necessary random access memory for this algorithm is proportional to the value of k2 . For example, if the value of k = 215 then for performing of this algorithm near 8 Gb of RAM is necessary.
That is why it is advisable to find the analytical formula for calculating the necessary random access memory size for RS -algorithms depending on the value of k . After research the following algorithms we for the first time received such a formula, that is for k -ary extended RS -algorithm the necessary random access memory size is calculated in bytes in such a way:
n = 4 • (З • k + n ( 4k ) + ^Q^
+|M| •(З + 2 • max{ M})), where п(x) - is a function of distribution of prime numbers, M – is a set of prime divisors of a number k in maximum possible power.
If k is a power of a prime number, then formula (10) is simplified to the following:
n = 4 • (5 • k + n( 4k ) + 3).
For the simplified extended k -ary RS -algorithm we have the following formula for calculating the necessary random access memory size:
n = 4 • (3- k + n( 4k )).
Table 7. Dependence of used RAM Size on k , bytes
|
k |
Algorithm |
|
|
RS |
Simplified RS |
|
|
2 |
56 |
28 |
|
4 |
100 |
52 |
|
8 |
180 |
104 |
|
32 |
664 |
396 |
|
1024 |
20536 |
12332 |
|
32768 |
655540 |
393384 |
|
131072 |
2621740 |
1573152 |
|
262144 |
5243280 |
3146116 |
|
1048576 |
20972220 |
12583600 |
|
2097152 |
41943968 |
25166740 |
|
4194304 |
83887328 |
50332884 |
The theoretically calculated necessary RAM size when performing the algorithms for the values of k , which are the powers of 2 is given in table 7.
While analyzing the received time indexes it was set that extended RS -algorithm for arbitrary composite values of k performs slower than for the values of k , which are the powers of prime number, that’s why the research of algorithms for the values of k , which are the power of a prime number was conducted (tables 8-11). It is obvious that with increasing of the length of operands the optimal value of k also increases.
Table 8. Optimal Values of k , which is the Power of 2 for k -ary RS -algorithm
|
Length of the module, bits |
Value of k |
Performing time, ms |
|
128 |
32768 |
0,091 |
|
256 |
65536 |
0,116 |
|
512 |
65536 |
0,147 |
|
1024 |
65536 |
0,199 |
|
2048 |
65536 |
0,305 |
|
4096 |
65536 |
0,558 |
|
8192 |
131072 |
0,996 |
Table 9. Optimal values of k , which is the Power of 2 for Simplified k -ary RS -algorithm
|
Length of the module, bits |
Value of k |
Performing time, ms |
|
128 |
32768 |
0,117 |
|
256 |
65536 |
0,132 |
|
512 |
65536 |
0,161 |
|
1024 |
65536 |
0,235 |
|
2048 |
65536 |
0,368 |
|
4096 |
65536 |
0,725 |
|
8192 |
131072 |
1,274 |
Comparing the time indexes of the optimal values of k for every algorithm (tables 8-11) we can see simplified RS -algorithm in all cases precedes its universal analogue and the best results shows for k , which is the power of 3.
In the Lehmer modification (figure 1) there are two parameters s and h are used, where s – is a basis of number system, h – is the amount of junior s-like bits of operands, which are reduced while division.
Table 10. Optimal Values of k , which is the Power of 3 for k -ary RS -algorithm
|
Length of the module, bits |
Value of k |
Performing time, ms |
|
128 |
59049 |
0,086 |
|
256 |
59049 |
0,108 |
|
512 |
59049 |
0,143 |
|
1024 |
177147 |
0,248 |
|
2048 |
177147 |
0,303 |
|
4096 |
177147 |
0,552 |
|
8192 |
177147 |
0,977 |
Table 11. Optimal values of k , which is the Power of 3 for Simplified k -ary RS -algorithm
|
Length of the module, bits |
Value of k |
Performing time, ms |
|
128 |
59049 |
0,096 |
|
256 |
59049 |
0,130 |
|
512 |
59049 |
0,202 |
|
1024 |
177147 |
0,238 |
|
2048 |
177147 |
0,373 |
|
4096 |
177147 |
0,652 |
|
8192 |
177147 |
1,267 |
For researching the extended Lehmer algorithm the software product was designed, which allows to determine the certain amount of least significant s -like bits can be reduced for fixed length of module m , to maintain the maximum performance. During the investigation for the fixed value of s and fixed length of module m the value of h changed from 2 to 0.5 - 1 , where l – is the length of the module. For example, according to received experimental data if 5 = 2 and the length of the module is 4096 bits than the optimal amount of junior bits which are to be reduced is 3226 bits (table 12). As we can see for every length of m it is impossible to analytically determine such values, it is possible to find only experimentally with the help of designed software.
Table 12. Time of Performance of Extended Lehmer Algorithm Depending on Parameter Values
|
s |
Parameter h , performing time t , ms |
Length of the module, bits |
||||||
|
128 |
256 |
512 |
1024 |
2048 |
4096 |
8192 |
||
|
2 |
h |
126 |
251 |
509 |
997 |
2023 |
3226 |
6551 |
|
t , ms |
0,067 |
0,155 |
0,388 |
0,925 |
2,478 |
7,076 |
22,808 |
|
|
3 |
h |
80 |
160 |
323 |
641 |
1227 |
2304 |
3998 |
|
t , ms |
0,068 |
0,166 |
0,373 |
0,947 |
2,502 |
7,313 |
22,926 |
|
|
4 |
h |
58 |
123 |
256 |
504 |
1015 |
1748 |
3215 |
|
t , ms |
0,076 |
0,176 |
0,372 |
0,960 |
2,501 |
7,067 |
22,582 |
|
|
8 |
h |
43 |
85 |
171 |
341 |
670 |
1245 |
2011 |
|
t , ms |
0,065 |
0,175 |
0,371 |
0,971 |
2,638 |
7,165 |
22,779 |
|
|
16 |
h |
30 |
63 |
128 |
256 |
508 |
897 |
1451 |
|
t , ms |
0,073 |
0,173 |
0,370 |
0,885 |
2,382 |
7,040 |
22,633 |
|
-
VI. C ONCLUSIONS
Among the methods that are based on modular exponentiation (figure 1), the best results is the Joye-Paillier method. At the same time for operands with length smaller than 512 bits’ algorithm №2 of realization of this method is leading, and for the operands with length above 512 bits – algorithm №1. The involvement of arithmetic modulo 2 in these algorithms gives additionally near 5% of performance increasing.
Comparing the search methods of multiplicative inverse in the ring of integers modulo m based on modular exponentiation and methods based on GCD searching (figure 1), the best results prove to be those based on algorithms of GCD searching of two numbers and the worst – those based on modular exponentiation. Within the class of methods based on GCD searching extended Euclidean algorithm leads over extended Lehmer algorithm with optimal values of parameters on almost 20%. At the same time the offered improved Bradley modification of extended Euclidean algorithm comparing to basic algorithm gives the increase of performance for almost 17%.
In the given investigation we for the first time have got analytical formulas for calculating the necessary random access memory when performing k -ary RS -algorithm and simplified k -ary RS -algorithm for searching the multiplicative inverse in the ring of integers modulo m .
Further investigations should be focused on analysis of the k -ary RS -algorithms, namely on values of k , which are the multiplication of two powers of prime numbers and on building the adapted simplified RS -algorithm, which will do the preliminary analysis of operands and determine the optimal value of k . Besides, it is necessary to build the analytical dependence function of operating time of algorithm and the length of operands and the value of k , which is used.
Список литературы The Analysis and Investigation of Multiplicative Inverse Searching Methods in the Ring of Integers Modulo M
- Darrel Hankerson Guide to EllipticCurve Cryptography / Hankerson Darrel, Menezes Alfred, Vanstone Scott // Springer-Verlag New York, USA. — 2004. — 311 p.
- Richard Crandall Prime Numbers A Computational Perspective / Crandall Richard, Pomerance Carl// Springer-Verlag New York, USA. — 2005. — 597 p.
- Guerric Meurice de Dormale, Philippe Bulens, Jean-Jacques Quisquater Efficient Modular Division Implementation ECC over GF(p) Affine Coordinates Application / Meurice de Dormale Guerric, Bulens Philippe, Quisquater Jean-Jacques // The 14th International Conference on Field Programmable Logic and Applications, FPL 2004, Volume 3203 of Lecture Notes in Computer Science. — 2004. — Pp. 231-240.
- Donald E. Knuth Art of Computer Programming, Volume 2: Seminumerical Algorithms / Knuth Donald // 3rd Edition by Addison-Wesley Professional, Canada. — 1997. — 784 p.
- Richard E. Blahut Theory and Practice of Error Control Codes / Blahut Richard E. // Addison-Wesley. — 1983. — 500 p.
- Henri Cohen A Course in Computational Algebraic Number Theory / Cohen Henri // Springer Science & Business Media. — 1993. — 534 p.
- S. Parthasarathy Multiplicative inverse in mod(m) / Parthasarathy S. // Algologic Technical Report #1/2012. — 2012. — P. 1-3.
- Robert Lorencz New Algorithm for Classical Modular Inverse/ Lorencz Robert // Cryptographic Hardware and Embedded Systems. International Workshop. — 2002. — P. 57-70.
- WolframMathWorld: http://mathworld.wolfram.com/CarmichaelFunction.html
- W. Fischer Note on fast computation of secret RSA exponents / Fischer W., Seifert J.-P. // Information Security and Privacy (ACISP 2002), vol. 2384 of Lecture Notes in Computer Science, Springer-Verlag. — 2002. — Pp. 136–143.
- Marc Joye GCD-Free Algorithms for Computing Modular Inverses / Joye Marc, Paillier Pascal // CHES 2003: Cologne, Germany. — 2003. — Pp. 243-253.
- Jonathan Sorenson Two fast GCD algorithms / Sorenson Jonathan // Journal of Algorithms 16 (1). — 1994. — Pp. 110-144.
- A.W. Bojanczyk A systolic algorithm for extended GCD / BojanczykA.W., BrentR.P. // Comput. Math. Applic. Vol. 14, No. 4. — 1987. — Pp. 233-238.


