The analytical description of the Earth's ring current proton flux for the pitch angle of 90 degrees

The terrestrial ring current, which is an electric current flowing westward around the Earth, basically locates at distances between ~ 2 and 9 Re (Re is the average radius of the Earth). Its origin, growth and decay are strongly associated with geomagnetic storms. The trapped energetic (~ tens of keV) positive ions ( H ⁺, He+ and O⁺) undergo an azimuthal drift and comprise the storm ring current. Three primary processes are found to be responsible for ring current decay: Coulomb collision processes and charge exchange, together with pitch angle diffusion by electromagnetic ion cyclotron waves [1].

Recently, numerous studies have performed on stormtime dynamics of radiation belt energetic particles and also for particles of the Earth’s ring current since their fluxes are found to vary strongly. Such strong variation of dynamics of radiation belts and the Earth’s ring current is considered as the contribution from wave-particle interactions, and from drift resonance associated with enhanced ultra, low frequency waves. However simultaneous observation and corresponding modeling of pitch angle scattering of ring current protons by electromagnetic ion cyclotron waves during a nonstorm period ( Kp < 3) have seldom been reported [2]. That is the primary purpose of this study.

1.    The mathematical model

The ID modified Fokker-Planck equation (or pitch angle diffusion equation) for the phase space density, describing “pure” pitch angle diffusion only with wave-particle interactions losses, can be expressed by [3, 4]

dZ dt

1__d_ sin a da

sin a • D_aa

df da

sin² a cos a dL Д

2L    "dT

— -Z—+ sv sin^{2 a} •^f.

^T wp

Here, f is the phase space density (referred to as distribution function), t is the time, L is the McIlwain parameter, a is the local pitch angle from 0 up to 180 degrees, D_act is the pitch angle diffusion coefficient [3, 4], ^dL/dt i^s the radial rate [3, 4], T_wp is the lifetime due to wave-particle interactions [3, 4], S_x is the perpendicular coefficient of the particle source function ( a = 90°) [3, 4].

The equation (1) is original model in space of velocities which contains some mathematical models of pitch angle diffusion as particular cases, e.g., [5-7].

Using (1), as new mathematical model is offered the ordinary differential equation for the analytical description of a perpendicular differential flux of the charged particles ( a = 90°) in the Earth’s magnetosphere which depends on time and several parameters:

A , Z__L dL +   7± - 7±q V dt       2L dt 7±o (7±o + 2) Twp ^      ’ whore jx is the perpendicular dilTerenl ia 1 flux of I lie charged particles (j = 2mEf. m is the charged particle mass. E is the particle energy). 7x0 is the well-known (when . = jx sin7 a) parameter of the charged particle pitch angle distribution (or the pitch angle distribution anisotropy index) but is taken for the 90° pitch angle at t = 0, 71 is the average parameter of the charged particle pitch angle distribution on an interval of time of calculation (it is supposed, that 71 « const).

The conclusion of the equation (2) is presented in an appendix.

Under the certain geophysical conditions and on a. time interval approximately no more than three hours (when a geomagnetic activity index Kp = const) or on a greater time interval, when Kp « const, the equation (2) can be solved analytically.

Then the analytical solution of the equation (2) is

•         „   ( (^Ф2ъ3 cos ф I     7± - 7±0    \A j±( ) j±0 xp к к 7948800 + 7±0 (?±o + 2) Twp) 7 '

Hero. J^o is the perpendicular differential flux of the charged particles at t = 0. ф₂ in [8]. arid ф is I lie azimuthal angle (local time LT = 0 h at midnight) or geomagnetic eastern longitude in the magnetic equator plane.

The conclusion of the equation (3) is presented in an appendix.

2.    Experimental data and calculations

Further it will be used correlated observation of enhanced electromagnetic ion cyclotron (EMIC) waves and dynamic evolution of ring current proton flux collected by Cluster satellite near the location L = 4.5 during March 26 - 27, 2003, a nonstorm period (D_st > -10 nT) [2]. It is shown, that energetic (5 - 30 keV) proton fluxes are found to drop rapidly (e.g., a. half hour) at lower pitch angles, corresponding to intensified EMIC wave activities.

For calculation we shall take following data [2]: j^₀(t = 0 s) = 5.5894 • 105 (cm² s sr keV)^-1, j ^ (t = 1800 s) = 2.1073 • 105 (cm² s sr keV)^-1. Kp = 2.GG or 3 -. L = 4.17. ф = MLT = 22.58 li. _7±0 = 0.5157. 7^ = 0.5801. E = 17.1 keV. Thon using (3) turn out T_w = 91.4988 s aiid dependence j ^ from t on I lie interval t = (0 - 1800) s (Fig. 1).

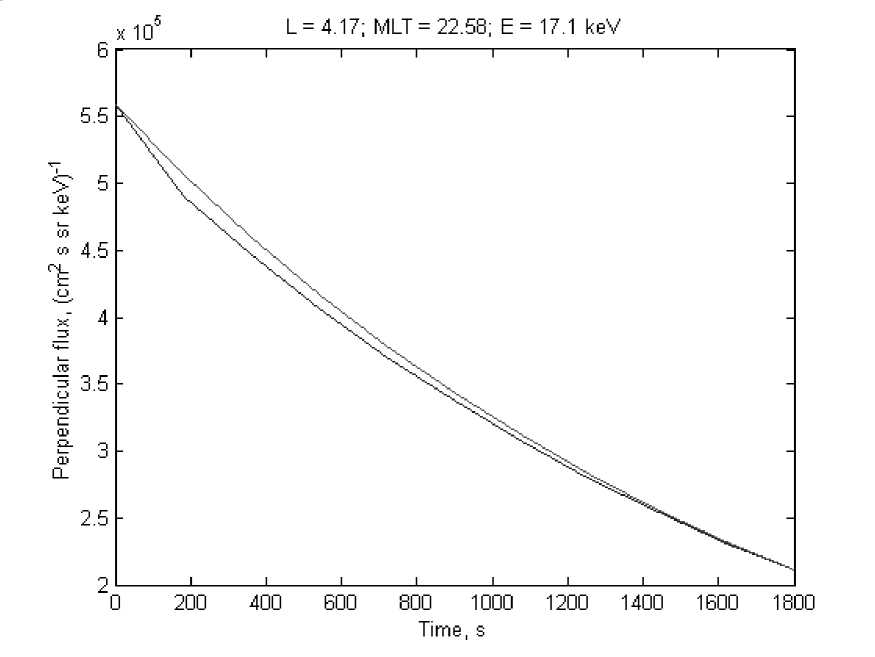
pitch angle on full model (1) - the bottom (blue) line and on

Рис. 1. Differential fluxes of protons for the 90

the offered model (2) or (3) - the top (red) line.

Comparison of results on the offered model (2) or (3) and on full model (1) for the pitch angle range from 0 up to 180 degrees is lead. For a. perpendicular differential flux of the Earth’s ring current protons very good consent with the maximal relative error approximately 3.23 % is received.

Conclusion

As mathematical model is offered the ordinary differential equation for the analytical description of a. perpendicular differential flux of the charged particles in the Earth’s magnetosphere which depends on time and several parameters.

The model allows to estimate also for different geophysical conditions a. lifetime due to wave-particle interactions T_w.

In the considered example for a. perpendicular differential flux of the Earth’s ring current protons very good consent with the maximal relative error approximately 3.23 % is received.

Appendix

A conclusion of the equations (2) and (3).

Considering, that j = 2mE f, m = const, E = const and the coefficient of pitch angle diffusion is offered to be determined [3, 4] as follows

Daa = D, sin2 a =--------- sin2 a,(Al)

7±o П,0 + 2) Twp first from (1) we receive the equation dj 1 d                  dj   sin2 a cos a dL j di = 5naда sin1""sin "aa--ы^и’) "^sin "•j-

Then we take derivatives and as a. result it is received

= ^d, sin² " 17+sin" cos " (w, - 21^ ) |a+

+ (- (2cos2" - sin2") 2L^ - ^ + S, sin2") j." '

At a = 90° and da |, = 0 the equation (A3) becomes simpler dj । _ dj _ n 92j     ( 1 dL 1\ dik =    = D, d"2 |, +V.2L1E - та,                           **

Proceeding from dependence j = j , sin⁷ a, 7 = const = 7 , it is possible to prove [7], that

Then using [3, 4]

d7i = da2 l,

-

7±j±.

(A5)

S , =

(7,0 + 3)

⁽7,0 ^{+ 2) T}W

and (Al), (A4), (A5), the equation (2) = (A6) turns out:

djA /

0E + 7

1 dL

2L dt ⁺ T_a ,

- S , + Dj_7j_^ j , = 0,

dj ,    f

"it ⁺

1 dL

2L dl ⁺

7,0     A •

7,0(7,0 + 2) T a,J ^J

7 ,

= 0 .

(A6)

To receive the equation (3), we shall take the following approached equality [3, 4], using the bounce-

averaged radial drift velocity of charged particles (measured in 1/s) in the Earth’s magnetosphere dL ~ / dL \_ Q^2L4COS, —   2^ф2L4 cos ф

(A7)

Et ~ \1Т/ = -Ф"ф0Ь COSФ = -24 • 60 • 60 • 92, where ф is the azimuthal angle (local time LT = 0 h at midnight) or geomagnetic eastern longitude in the magnetic equator plane, Q is the Earth’s angular velocity, ф0 = 92 kV, and the dependence of ф2 (measured in kV) on geomagnetic activity, i.e., on the Kp index, is determined from the formula [8]

_           0.045

• ²    = (1 - o.i6Kp + 0.0iKp²'f .

Believing all parameters in the equation (A6) constants (or approximately constants), we find the exact (or approached) analytical solution of the equation (A6) = (2) in the form of (A8) = (3):

• •                  (^^ф2^3 cos^ф ,      7± ^- 7±o    A A

• ³^ ^{)   J±}0 xp V ( 7948800    7±o (7±o + 2) T^J ) "                " "