The blow-up solutions to nonlinear fractional differential Caputo-system

The original conception of fractional calculus was appeared prior to the turn of 20th century, when L’Hopital wrote a letter to Leibniz asking him about a particular notation he had used in his application for the nth-derivative of the function f (x) = x. L’Hopital posed the question to Leibniz about the result when n = 2 . From that time, fractional calculus become the most famous notation attracted more and more mathematicians and physicists who have discovered many disciplines, because fractional differential equations provide an excellent tool used to describe various phenomena such as rheology, damping phenomena, diffusion processes, etc. From this fact, we have many definitions of the concept of noninteger order integral or derivative according to the notations and methodology of the researchers, and the most common are given by Riemann–Liouville and Caputo which will define later. The difference between these two definitions is connected with the order of calculation.

The study of fractional ordinary differential systems have been widely used in different fields of science, and the existence and uniqueness of local solutions to the integral equations are proved by many researchers, see [1–11] and the references therein. Recently, Abbas [1] establishes the existence of solutions to fractional order ordinary and delay differential equations with some applications. In [2], Mahto, Abbas and Favini use Sadovskii’s fixed point method to investigate the existence and uniqueness of solutions to Caputo impulsive fractional differential equations. Mahto and Abbas [3] introduce a PC-almost automorphic function and establish the composition theorem. As an application, the authors study the existence of almost automorphic solution to impulsive fractional functional differential equations under the condition that the forcing term is almost automorphic.

Our main objective is to find finite time blow-up of solutions to the following Caputo fractional differential equation:

f ut(t) +c D+ u(t) +c De+ u(t) = DY+ |v(t)|q, j Vt(t)+c /- +v(t)+c Dpav(t) = DY+ |u(t)|p, t E R+,                 (1)

[ u(0) = U o , v(0) = V o .

where p, q > 1, u ₀ , v ₀ > 0, 0 <  a i , e i , Y i < 1, a i < e i and , i = 1, 2. Our result is new and compliment the existing one.

In order to motivate our results, it is convenient to recall some facts about the fractional ordinary differential system. In [12], the authors study the profile of blowing-up solution to nonlinear system of fractional differential equations (FDE in short):

( uxo+ c D a (u)(t) = iv(t)i q ,

' ^v'(i)+ c D ^e + ^(v)^(t) = ^{| u}(i) ^{| p} , t E R + ,

[ u(0) = u ₀ > 0, v(0) = v₀ > 0

and prove that the solutions to the precedent problem blow-up in finite time, if 1 — pq <  a + ^e or 1 — <в + ^a .

p         pq         p

In [13], the authors multiply the caputo derivatives terms ^c D 0 + (u) (t) and ^c D ^e ₊ (v) (t) by the continuous functions A(t), B (t), respectively, and obtain the following system:

f u ‘ ^(t) + A^{(t) c} D a + ^{(u) (t)} = ^{l v ( t )l} q ,

J v ‘ (t) + B (t) c D o ^e + (V), (t) = |u(t)| ^p , t e R + ,

[ u(0) = u ₀ > 0,v(0) = v ₀ > 0.

Г                \ ¹     /         \ ¹      Cc V^q<1       CcEpp

Under the condition h = min <  T, ( ^З -^ ) ^{1 a} , ( ^Г( 2 — ^в) ) ^{1 в} , —---—, —--- — г , the

2M           2M            c         c authors of the work [13] guarantee the existence of local solution to their problem. Then, the authors used Lipschitz condition on A(t) and B(t) to prove the blowing-up results.

After that, the authors of the paper [8] generalize the system of Qun and Huilai [13].

nn

The authors take A(t) = ^a i (t) , B (t) = ^2b i (t), and express the right hand side of the i =1                   i =1

system by the Riemann-Liouville operator of the functions f and g. The problem takes the following form:

• ( u , (i) + a i (t) ^c D a + (u) (t) + ... + a n D a + (u) (t) = J ₀ ^{1 - Y 1} f (u,v),

• ^ v t (t) + b i (t) ^c D 0 + (v) (t) + ... + b n (t) ^c D e + (v) (t) = J ;¹¹ g (u, v), t e R +

• 2.    Some Preliminary Results

[ u(0) = u0 > 0,v(0) = v0 > 0, where p, q > 1, 0 < ai < 1,0 < bi < 1, i = 1,..,n, f and g are arbitrary analytical functions. Their method of proof is based on Arzela Ascoli and Shauder theorems for the existence of local solution. Then, the authors use the weak formulation of the systems with a good choice of test function for the blowing up result, for more details see [8].

In this paper, we mix the two precedents systems. We take n = 2, J j -^{7 1} f (u,v) = D Y + |v(t)| q , J -^{7 2} g(u,v) = D j + |u(t)| ^p , a 1 (t) = a ₂ (t) = b 1 (t) = b ₂ (t) = 1 to obtain system (1). We determine the sufficient conditions on parameters of system (1) to show the non existence of global solution to system (1). The paper is organised as follows. In Section 2, we present definitions, properties of fractional derivative equations, and some lemmas needed for our work. Section 3 is devoted to proof of the main results on the blow up in finite time of solutions to system (1).

In this section, we present several lemmas for the proof of Theorem 1 and Theorem 2. Let AC[0, T ] be the space of all functions which are absolutely continuous on [0, T], where 0 to. Then, for f G AC [0, T ], the left-handed and right-handed Riemann-Liouville fractional derivatives D 0 + f (t) and D T - f (t) of order a G (0,1) are defined as follows:

t

• D^ f (t) = _Tl? , T [ (t - s) ^- ” f (s)ds. t G |0,T],               (2)

Г (1 — a) dt J

T d f

D T - f(t) = p₇₁-----v(s — t)   f(s)ds, t G [0,T ].                (3)

Г (1 — a) dt J

t

It is shown in [5, Lemma 2.2], see also [6], that, for f G AC ([0,T]),

D f ^(t) = 1^)

t t^-a f (0) + 1 0

(t — s)- ^a f ‘ (s)ds

Note that

t

• D 0 + (f (t) — f (0)) (t) =      *   . pt — s) "“ f ‘ (s)ds . D f (t),

which is the Caputo derivative of f . For the right-hand derivative, we have

Da - f (t) =         v

Г (1 — a)

f (T)           )-««w

(T _— t) “    J ^{( t — s)   f ( s ) d} s

t

In [5, Corollary 2, p. 46], it is shown that, for the functions f,g G C ([0,t]) the derivatives D ₀ + g, D T - f exist at every point of [0, T] and are continuous. We have

T j f (t)D0+ g(t)dt = which is the formula for integration by parts.

T

D r - f(t)g(t)dt,

Lemma 1. Let ^(t) be a function such that

.«, = {0'-""‘-

01T" ^T , ^X ^ 2.

Then we have

T l DT-V (t) dt = Ka,XT 1-a,

K = ______ ^{ХГ(Х — a)} ______

“^,Л (X — a + 1)Г(Х — 2a + 1)^.

Lemma 2. Let ^(t) be a function such that

.«, = {0¹ -"'■

0 " t" T, X > 2, t>T,         ,

and suppose that p >  1. Then, for A >  p — 1,

T p

^ ^{1 - p} (t) Ht)| ^p dt = Л р T ^{1 - p} ,    Л р = ----- —,

J                                 ^A — p ^{+ 1}

and, for A >  ap — 1

T j ^-       w Ipdt=лраТ-p.     =[г<_л ^

3. Blow-up Results

This section is devoted to proof of the blow-up of solution to system (1).

Theorem 1. Let T >  0, assume that

Y 2 > max (a 2 , в 2 ) or a 2 < Y 2 < в 2 ,

Y 2 + Y 1

< min{1 + a 2 ,1 + в 2 , в 1 I— оI

2 pq

— 1},

1 < q <  min

f 1 - Y 1    1 - Y 1

γ 2 - α 2 ^, γ 2 - β 2

.

Then all solutions (u,v) G C ([0, T]) to (1) blow-up in finite time.

Proof. Let us carry out the proof by contradiction. Suppose that (u; v) is a non trivial weak solution to (1), which exists globally in time. First, we have c Du = Do+ (u — uo).

Then, we can rewrite problem (1) as follows:

u t ^{+ D} 0 + ^{(u —} u o ) ^{+ D} o + ^{(u —} u o ) = ^D o + ^{| v |} q , v t + D . ^{(v —} v o ) + D ^e + ^{(v —} v o ) = D ^Y + ^{| u | p} , u (0) = u o , v (0) = v o .

Let T >  0 , then

T        T

T

T

j u t ^dt + j D“ + (u — u ₀ )^dt + j D 0 + (u — u ₀ )^dt = j D ^- |v| ^q ^dt

and

т

T

T

T

I v t ^dt + j D a (v — v o )^dt + j D^. (v — v o )^dt = J D Y + I u \p ydt.

By using (4) and simple calculations we can obtain

т

J |v| ^q D Y - ^dt + u _o

(1+J

T

D O — ^dt + J D ^e — ^dt

=

= J uD T — ^dt + J uD T - ^d.t — J up'dt,

and	0 Y l u l p D Y - vdt + v o (1 + 0 Y D Y -vdt + 0 Y D Y - vdt^ = = Y vD Y - vdt + Y vD Y - vdt - Y vv ’ dt. 000

Applying H¨older’s inequality with parameters p and p ^′ (rsp. q and q ^′ ) to the right hand sides of (8) and (9), we derive

T

T

and

uD _T ^{α 1}- ϕdt

≤

T

uD _T ^{β 1}- ϕdt

≤

T

uϕ ^′ dt

≤

T

vD _T ^α - ϕdt

≤

T

vD _T ^β - ϕdt

≤

T

vϕ ^′ dt

≤

j u (D Y -    p (D" .

1 /p

D _T ^{α 1} -

ϕdt ≤

T

1 /p

j |u| ^p (D T - v) dt

T

j u (D Y - vf* (D Y - v)

T

1 /p

T

1 /p ^′

j DY - v)

1 /p _{D T}β 1 _-

-

^{p , /p} | D _T - v | ^p ' dt

ϕdt ≤

,

J |uf ⁽D T - v⁾ dt

T

У u (D Y - v) 1 ^/p (D T - v)

T

1 /p

T

1 /p ^′

j (D Y - v)

1 /p

ϕ ^′ dt ≤

-

p/p ^′     β

D Y - v

p ^′

dt

,

J |u| ^{p (}D T - v⁾ dt

T

1 /p ^′

T

У v (D Y - . ■   (D Y - v)

T

1 /q

j (D Y - v)

1 /q

_{D T}α _-

-

p ^′ /p

ϕdt ≤

| ϕ ^′ | ^{p ′} dt

,

j |v| ^q (DY-v) dt

T

j v (D Y - v)^1/q (DY- v)

T

1 /q

T

1 /q ^′

j |v| ^q (D j - v) dt

T

I v (D Y - v)^1/q (D Y - v)

T

I |v| ^q ^DY- v⁾ dt

j (DY- v)

1 /q _{D T}β _-

T

1 /q

-

q ^/q \ D Y -vf dt

ϕdt ≤

1 /q ^′

,

j (DY- v)

1 /q

ϕ ^′ dt ≤

T

-

q ^′ /q _D β _-

T - ^ϕ

q ^′

dt

1 /q ^′

,

j (DY- v)

-

q ^′ /q

| ϕ ^′ | ^{q ′} dt

.

Let

I i =

T j |u|p (DT-y) dt, 0

J i =

T j |v|q (DY-y) dt, 0

T

I/ = I DY - yf p ' /p \ DT- y | ^p ' dt, 0

T

I 3 = j (DT- уГ^ \ D ^e _T 1 - y \ p dt, 0

T

I 4 = j (D Y- yr p^/p |y ‘ | ^p ' dt,

Then, we can rewrite (8) and (9) as

J / = j D-. \ D _T - . ' dt, 0

T

J 3 = I (DY- У) q ' q D T ²- У q dt, 0

T

J 4 = j (DY-y] - ' /q |y ‘ | ^q ' dt.

and

J i + u o

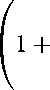
TT j DT - ydt + J DT- ydt

< i i ^/p Iy^/p' + y^p + i 4 ^/p') ,

I l + v o

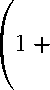
TT

I DT- ydt + У

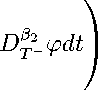
< J i /q (J 2^{1 /q} ' + Js /q ' + Jf q ') •

Using (10) and (11), we obtain the inequalities

Ji < ID ^ + I31/P' + Ii/p') and               ii < Jy Jy + Jy + Jy), from which we have

T ^{i - i /pq} / ( T /p p'  I   T /p p'  I   T /p p' ) ( -f/H  I   1М^ I  T^i/q' ) /p

J i < II /    ⁺ I 3    ⁺ I 4 J /    ^{+ J} 3   ⁺ J 4        •

Next, using Lemmas 1 and 2 in the right-hand side of (14), we find j1'-1/,<- < c (t(Yp2-i)+v + T(Yp2-a 1)+Y + T(YP2-e1)+v) < (t(Yq‘-i)+? + t(Yq"-a2)+7 + t(Yq"-e2)+7)i/p.

Then, we can write

1 - 1 /pq J ₁

< C (T ^S 1 + T ^S 2 + T ^SY Tr ^S 4 + T ^S 5 + T ^S6) ,

where

S i = ( ^{Y /} - 1) +1;      S / = ( ^{Y /} - a i ) +1;     S 3 = ( ^{Y /} - e i ) + ^;

p          p ^′                 p           p ^′                 p           p ^′

S ⁴ = [(^YT - 1) ⁺ 7] p^{; S} 5 = [(^YT - ^{a /} ) ^{+ 1} ] p^{; S} 6 = [(f - ^{в /} )⁺ 7] p •

Therefore,

_{J 1}1 - 1 /pq _{≤ C}

T S 1 + S 4 1 t S 1 + S 5 1 t S 1 + S 6 1 t S 2 + S 4 1 t S 2 + S 5 + +T S 2 + S 6 1 t S 3 + S 4 1 t S 3 + S 5 1 t S 3 + S 6

)

Note that S i + S 4 < 0, S i + S 4 < S i + S 5 , S i + S 4 < S i + S e , while S 2 + S 4 < S 2 + S 5

S 2 + S 4 < S ₂ + S e , and S 3 + S 4 < S 3 + S 5 , S 3 + S 4 < S 3 + S e

Then, we can write

Si + S5 — Si + S4 +— (1 - «2) < 0,  Si + Se — Si + S4 +— (1 — в2)

pp

S2 + S5 — S2 + S4--(1 — a2) < 0,  S2 + Se — S2 + Se — (1 — в2)

p

S3 + S5 — S3 + S4 +—(1 — «2) < 0,  S3 + Se — S3 + S4 +—(1 — в2) < pp

which, respectively, are equivalent to

« 2 > Y 2 + -(Y i — 1),  в 2 > Y 2 + -(Y i — 1),

where

1--< ai H— (e2 — Y2) — ~, pq p           pq

1-- < a i +— (« 2 — Y 2 )--,

1	--< e i H (a 2 — Y 2 ) — —, 1-- < e i + (в 2 pq       p           pq      pq       p	— Y 2 )	γ -
Now, let			pq γ pq,
	H i — a i + - ( « 2 — Y 2 ) — —, H 2 — a i + - ( в 2 —
		Y 2 ) —
	p           pq             p
	H 3 — e i H(a 2 — Y 2 ) — ~,  H 4 — e i H(в 2 —	Y 2 ) —	γ .
Then, 1 —	p           pq             p 1 — <  min{H i , H 2 , H 3 , H 4 }. Now, from (11),		pq
	pq

then

v o ( j D _T - ^t + j D T 2 - ) <  j* J' + J 3" + j 4 /q ‘ ), 00

v o j Da ^dt < j ; /q J" + j¹" + j 4 /q ‘ ). 0

From Lemma 1, we obtain

V o < CT ^{a 2 - i} J l /q J ₂ ^{i /q} ‘ + J ₃ ^{i /q} ‘ + J ₄^i/q^) ,

and

v ₀ <  cJ /q t ^a 2 ^{- 1} (t ^{( Y}q^{1 - i ) +} q’ + t ^{( Y1 - a} 2 ^{) +} q’ + t ^{( Y}q^{1 - e} 2 ⁾⁺^,

v 0 ≤ CJ ^/q

(T a 1 ₊ T a 2 ₊ T a 3 ) ,

where oi = а2 - 1 +-- q

γ 1 ^2 = а2 — 1+1-- ^q

γ 1 ^ з = а 2 — 1+1-- ^q

We note that а ₂ = 1 ( y i — 1) < 0, а 1 = prove that а ₃ <  0. Then, by sending T A similar analysis can be performed by

• 1 ) +—; = a2 — 1 +— (Yi — 1) , q′

• a2 I + - = - (Y1 — 1) , q′

• в2 ) +~ = a2 — в2 +(Y1 — 1) . q′

= a ₂ — 1 + 1 ( y i — 1) < 0. Using (5), we can easily ^ to, we arrive at the contradiction 0 < v ₀ < 0. showing that I 1 is bounded, if

1 — _ <  min{H 1 ,H 2 ,H 3 ,H 4 },

where                   1            Y H 1 = a 2 +— (a i — Y i ), p           pq 1               Y 2 H 3 = в 2 + - (a i — Y i ), p           pq which, via (10), leads to the contradiction:

1Y H 2 = a 2 + - (e — Y 1 ), p           pq H 4 = e 2 + - (e i — Y) — Y 2 , p           pq 0 < u o < 0. This completes the proof of

Theorem 1.

□

Theorem 2. Assume that max{Yi,Y2} < min {a^i} for i = 1, 2.

Then problem (1) does not have a global solution.

Proof. Let us prove by contradiction. Assume that T _max = + to, and consider the test function used in [7]:

( (1 — t/T ) ^A ,   0 <  t <  t,

+ (t) = S                           A> max(Y i ,Y 2 ).

I 0,               t > T,

Then, we multiply the first equation of (1) by у and intergrate over (0,T). We have

TT

J U t ^(t)dt + J D a (u (t) — U o ) + D ^e + (u (t) — U o )

T

= J |v| ^q D T- ^^dt.

T

y(t)dt = J D 0 + |v| ^q y(t)dt =

A simple calculation gives that, forλ > γ j

DT—W)= CxyT-A (T — t , where Cx,Yj = T^^Y—YYYYJ,j = 1, 2. Since u0 > 0 and у G C 1, then we integrate by parts and have

J |v| ^q C a,_Y i (T — t) ^{Y 1} +(t)dt < — J ua(t)dt + J u (t) D T- +(t)dt + J u(t)D T — ^(t)d^t;.   (21)

Let p ^′ be a conjugate of p, then

T

T

J u (-/(t)) dt = J u^t^'Mt) ^1/p X ⁽T ^- t)

^{Y 2 /p} (T - t) ^Y 2 ^/p (-^ ‘ (t)) dt <

<

C λ,γ 2

j |u| ^p (T - 1) -" WW + (C4;; ) p 'p j (v(t)) -^Ph> (T - t) ^Y 2^Y l^ ' (t)l ^p ' dt,

₀                                           ,γ 2         ₀

and

T

T

J u (t) D T — ^(t)dt = I u ^(t) м/г p Ht)

^{1 /p} x (T - t) ^{- Y 2 /p} (T - t) ^{Y 2 /p} D T - ^(t)dt <

< C a,y 2

T                                    p /p T j |u|p (T - t)-Y2 ^(i)di + (C^)" P j (V(ty)-Ph- (T - t)M |D?L^(i)lp'dt,

₀                                           ,γ 2         ₀

T

T

j u (t) D T ¹ _- ^(t)dt = I u ^(t) H^t)V p V ^(t)

^{1 /p} X (T - t) ^{- Y 2 /p} (T - t) ^Y 2 ^/p D T - ^(t)dt <

T                                 p/p T

< -^ J |u| p (T - t) -^{Y 2} Odt + (C^)    J (^(t)) -^p ' '^p (T - t) ^Y 2 ^p l DT- 7(<)l p ' dt.

Using the same steps, we find

T

- a,y i ЛИ’ (T - t)

-

^{Y 1} ^(t)dt <

3 C a,y 2

T

I |u| ^p (T - t) ^{- Y 2} _V (t)dt+

p ^′ /p T                           _{- γ p} ′

+ (C^)   I (^(f^ 'p (T - t) ~ l^‘(t)lp'd<+ p′ p T        -p           -γ p

+ 7^ J Mt))“ (T - t)~ (|DT ¹ - ^(t)l ^p ' + |D t - ^(t)l^p) dt.

C λ,γ 2      0

Let q ^′ be a conjugate of q , then

T

C a,y 2 /Mp (T - t) -^Y 2 WW <

3 - a,y i

q ^′ /q _T

+ 7^    / (^(t)) ^-qVq (T - t)

C λ,γ 1       0

J

h vr (T - t) -Y 1 ,(t)dt+

-γ1 q′              ′ q |^‘(t)|q dt+

q

+

q   ^T           -q^′

)  /(Ht))“ (T - t)

C λ,γ 1      0

γ 1

We put

T

A := C a,y i j |v| q (T - t) ^{- Y} 1 ^(t)dt;

T

B := C a,y 2 j |u| p (T - t) ^{- Y 2} ^(t)dt;

-γ1 q′ q

D “- ^(t)| q ‘ + |D T- ^(t)| q ‘) dt.

T

C := у (^(i)) -^p ' ^/p (T - t) ^-Y2 pⁱ ^‘(t)| ^p ' dt;

T

D := /(v"(i)r^Vq (T - t)- qq- l _V4t) l q'dt;

T

E :

-p′             -γ p′

(^(t)) - (T - t) ~

T

F :

-q′              -γ q′

= J (Ht)) “ ( t - 1) ~ 0

(|D T- ^(t)| p ‘ + |D T- v(t)| ^p‘) dt;

(|D T- v(t)| q ‘ + \ D T - v(t) I q ') dt.

From (23) and (24), we have

A < ³ B ~ 4

p ^′ /p                                                 q ^′ /q

⁺ (Cd  ^{(C+ E )}, ^B < 4A⁺(Cd   ^{( d + F} >.

Therefore,

A ≤

B ≤

" (CH

" (')

q ^′ /q

p ^′ /p

1 D+F■ (CH (C +     (H)

p ^′ /p

(C + E ),

q ^′ /q

(D + F ).

Using integration by parts in system (1) and (25), we write

^T                                      q ^′ /q                                 p ^′ /p

U0 j DT-V (t) dt < -7, C—J   (D + F) + -T C-)   (C + E), о                                                               ’                                                                     ’

T vo j Dla-V (t) dt < 12 (C^) о                                       ,Y2

Using Lemma 2, we find

C <  cT ^{- Y 2} p ⁺¹^ ^p' ;

p ^′ /p                                   q ^′ /q

<^C+E> + - (c^)   ( ^{D + F} >.

′

D <  cT ^{- Y 1} qr ^{+1 - q} ;

E ≤ c

′

′

T —7 2 pp + 1 -p ‘ a i | T -7 2 pp + 1- р'в 1

)^{; F} <  ^c(

′

′

T —Y i — +i- q ‘ a 2 । t — Y i — +i —q ‘ e 2

)

for some positive constant c . Consequently, we find

T u0 ^ DT- ^ (t) dt 0

_<  12 ⁽  4  ^{) q} ‘ ^/q

<  7 Ua,₇J

′

_c T - Y 1 - +W

'' + ^T^{- Y 1}

′

′

- + 1- q'a 2 । t -7 1 — + 1- q'e 2

JI

+

16 ⁽ 4  ^{) p} ‘ ^/p

7 кС л,72У

/

_c T -7 2 p + W

'‘ + ^T^{- Y 2}

/

/

p +1- p'a i | T -7 2 p + 1- р ‘ в 1

.

Therefore, uo < Ca1-^c

( ⁴ )     (t -7 1 q- ^{+ a} 1 ^- q ‘ + (t -7 1 q- ^{+ a} 1-q' ^a 2 + t -7 1 q- ^{+ a} 1 ^- q ‘ ^e 2 )) +

। ¹⁶ ( ⁴ )     ( m -Y 2 p + a 1 - p ‘ , ( -Y 2 p + a 1 - p ‘ a 1 , ^- 7 2 p + а 1 - р ‘ в 1 ))

+ 7 ^Са,₇2У   к           ⁺k             ⁺             УУ J

T

′

′

′

vo < C-^C 12 ^ 4 ^     ^T-Y2P‘/р+«2-р' । ^tY2p‘/p+a2-p‘ai । tY2P4p+«2-p'P1 ^ | I 16 ( 4 A     ^T-Yiq'/q+a2-q' | ^T—Yiq'/q+a2 -q'«2 । T—Yiq'/q+«2-q' в2 AA 7 \CX,71/                                                               '' Finally, using the fact that q′ -γ1 + ai - q < 0, —Y1 q + ai - ja2 < 0, —Yi — + ai - qв2 < 0, q qq p -γ2 ′ + ai - p < 0, —Y2p + ai - pai < 0, -72p + ai - pв1 < 0, p pp q -γ1 ′ + a2 - — < 0, -Yi— + a2 - —a2 < 0, -Yi— + a2 - — в2 < 0 q qq and taking T ^ to we arrive at the contradiction: 0 < u0 < 0 or 0 < v0 < 0.

□

Remark 1. Theorems 1 and 2 remain valide for the new system cD« u +c De1 u = D^ |v|q, cDa2v +c De2v = DJ+ |u|p, u(0) = uo,v(0) = vo.

t ∈ R +

under the same initial conditions on the parameters.

Acknowledgements. The authors would like to thank the associate editor, and anonymous referees for their constructive corrections and valuable suggestions that improved the manuscript.