The combined use of the wiener polynomial and SVM for material classification task in medical implants production

Published Online September 2018 in MECS

The process of the creating new materials for aggressive environments at different temperatures imposes certain some requirements on their microstructure and properties. Prospective for this purpose is stainless steels, pure titanium, and alloys based on it. These materials are widely used in various industries, especially in the production of rocket and aircraft engineering [1].

Today, titanium and titanium alloys have been used in medicine [2]. This is due to their unique properties, in particular, biological inertia in relation to the human body, a high specific strength and a corrosion resistance in a variety of aggressive environments, including sterilizing substances, plasma, and blood [2]. Firstly, this contributes to the widespread use of titanium alloys for medical products, including implants, dentures, etc. Secondly, the systematization of numerous experimental studies and the results of clinical trials [3, 4] allows the creation of large databases containing the functional properties of these materials.

These factors create the preconditions for the artificial intelligence tools [5, 6] to be used for processing such databases for the synthesis of new materials or their operational properties identification from a huge set of available and investigated features. In the manufacture of products, it will allow making a decision quickly about choosing the optimal material’s composition with predefined properties. As a result, it will be possible significantly to reduce financial resources and time in comparison with traditional investigation and design methods.

The current state of machine learning algorithms includes many similar methods [7] so their proper selection, adaptation or improvement is an important problem to solve this task.

The remainder of this paper is organized as follows. Section 2 describes related works and problem statement. Section 3 is devoted to the proposed methods. Section 4 presents an experimental research. Conclusions and future work are given in the final section.

• II.    Related Works and Problem Statement

The problem of developing methods for the effective classification of titanium alloy powders is described in [8, 9]. In particular, in [8], a computational intelligence method for determining the optimal microstructure and titanium alloy powders properties is developed. The tool used for this is the Probabilistic Neural Network. The advantage of the method is to assess the probability of assigning the input sample to a particular class. This enables an expert to make timely and correct decisions about the use or non-use of a material for the elements design of the necessary equipment. However, it makes a subjective assessment in the development of the product, and in combination with the low classification’s accuracy (about 70%) imposes a number of restrictions on the use of the proposed classification tool.

In [9] the authors describe a method for the identification of titanium alloys powders based on the use of a Kolmogorov-Gabor polynomial (Wiener polynomial) and the Random Forest algorithm (RF). The results of the task solution due to the use of this method have been significantly improved (more than 95% accuracy), however, the selection and setting of optimal parameters of the method do not provide a complete solution to the task. In addition, increase the number of the RF's trees to achieve a higher classification accuracy results causes to increase the time delays during its work. This situation is complicated in the case of Big Data or data streams processing [10, 11].

The aim of this work is to develop methods of the titanium alloys classification for the medical implants production. Such methods should, firstly, to provide high accuracy for designing products. Inappropriately identifiable material properties during its classification may cause defects during operation and reduce the expiration date [12]. Consequences and health damage in the case of a malfunction, breakage or complete failure of medical products are not to be estimated. Secondly, the developed methods should provide high speed in the training mode.

The advantage of using machine learning techniques to solve this task lies in the fact that they allow combining various factors (characteristics of titanium alloy powders) that effect on the properties of the materials which made from such alloys. This, in turn, increases the sensitivity of such methods to rather rare combinations of factors, which can provide a more accurate classification.

The main argument of using SVM as a tool for effectively solving a given task is the ability of this tool to work with a much smaller data sample compared to, for example, neural networks [13, 14].

• III.    Proposed Methods

Support Vector Machine (SVM) is one of the most widely used methodologies for data classification in Material Science [15, 16]. The linear SVM classifier proposed by V.N. Vapnik in 1953 gained its development in the early 1990's by creating a non-linear classifier using arbitrary kernel functions.

The basic idea of the method is as follows. It is necessary to find such a separating line between points on the plane, which will provide the most accurate procedure for assigning points to the corresponding classes (below and above the line). Such a line, according to the idea of this method, should be constructed as far away as possible from the points nearest to it from the two classes. This operation principle provides a more reliable classification [17]. When the spaces of high dimensions are considered, instead of the line, we consider the hyperplane, which will divide the classes of given objects. Detailed mathematical descriptions of the method are given in [18].

Among the main benefits of using this toolkit in the Material Science field are:

• –    the method provides uniqueness of the solution;

• –    the method is characterized by very high speed;

• –    the method provides the possibility of processing large amounts of information;

• –    the method provides some versatility by the possibility of using both existing kernels of functions and offering their own;

• –    there are developed optimal schemes of memory allocation and computational procedures for SVM realization to improve the efficiency of the method.

However, SVM has a number of disadvantages, the most important of which for solving the classification task is the low accuracy for noisy input data.

The multiparametric dependences of each data vector (Fig. 1), which are characteristic of this task, sometimes lead to an ineffective solution of the task, in particular by tools of computing intelligence [19]. In [8], the solution accuracy of the classification task (on the same data as in the work) using the Probabilistic Neural Network was 70%.

Incorrect identification of the material class, in this case, can lead to a number of defects in medical implants created on its basis. This can lead to both large material losses and a threat to human life (in the case of the presence of defective planes in vital organs). The need to increase the results accuracy of the materials classification task, cause to the use of effective tools for solving this task. Wiener polynomial (WP), as a universal approximator, can increase the solution accuracy of this task [9]:

n     nn

Y ( x_t,..., x_n ) = a, + E а,х, + XX a i , j x i x j + i = 1              i = 1 j = i

• + E X Ём« + ...            (1)

• i    = 1 j = i l = j

nnn  n

... ⁺xxx ... x a i , j , , ,...,z xix jxi ... x.

i = 1 j = i l = j   z = k - 1

where k is a polynomial degree, x ,..., x is the variables.

This is justified by the Weierstrass first theorem [9]. However, procedures for finding the coefficients of this polynomial by existing methods [20], especially in cases of large dimensional data, are not always effective.

That is why the paper proposes a method for data classification based on the combined use of Wiener Polynomial and SVM. This will ensure sufficient speed of the classification method by using SVM, as well as increase the accuracy of the solution to this task by using the Wiener Polynomial.

The algorithmic realization of the developed method involves the following basic steps:

• 1.    The input attributes (20 characteristics) consider as members of the Wiener polynomial (excluding zero member);

• 2.    Classification of a vector based on the search using SVM of a Wiener polynomial’s zero-member and coefficients for non-zero members.

The performance of the proposed method will depend on the implementation of step 2. As you know, SVM results largely depend on the choice of both the kernel and the value of the regularization parameter for the geometric difference [18].

That is why, for the investigation of the classification materials method for the search of the Wiener polynomial coefficients (step 2), two SVM implementations from two different Python libraries: LIBSVM [21] and LIBLINEAR [22] were used. These libraries contain similar SVM-based classifiers: C-Support Vector Classification (SVC) in LIBLINEAR (with the different kernels) and Linear Support Vector Classification (Linear SVC) , which, in fact, is another implementation of the SVC classifier with the linear kernel. Detailed mathematical descriptions of the SVC method are given in [23], and the Linear SVC method in [24].

The main distinguishing feature of both implementations is a different set of parameters that are used to solve the classification task. The parameters of both methods are given in Table 1 of Appendix A.

The combined use of Linear SVC and Wiener polynomials let's called Method 1 , and the use of SVC (with the different kernel) and Wiener polynomial let's call Method 2 .

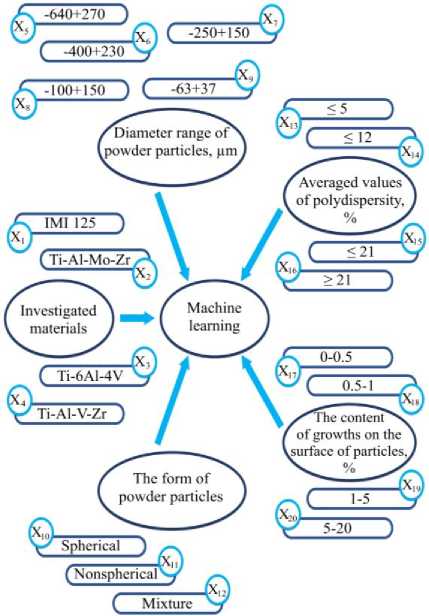
Fig.1. Elements of Data Set for modelling

• IV.    Experimental Results

For modeling of the proposed methods, it was used the DataSet from [8, 9]. Based on the studies from [8, 25], it was possible to distinguish four groups of characteristics that effect a composition of an alloy, which can be synthesized from four different titanium alloys powder components (Fig. 1).

In our case, every group contained from three to six characteristics, which in sum gave 20 independent attributes that were attributes of each input vector.

In [9], 480 observations were conducted. Each of them has one of four alloy characteristics according to the required properties (Table 1). Such an alloy are based on four different materials IMI 125, Ti-Al-Mo-Zr, Ti-6Al-4V, Ti-Al-V-Zr. Thus, Data Set of 480 observations, each containing 20 inputs and one output, that describing the class of the resulting alloy (Table 1), was constructed.

To simulate the described methods, the dataset was randomly divided into the test and training samples in accordance with 20 and 80%. A numerical representation of the representatives of each class for both the test and the training samples are showed in Table 1.

Table 1. Numerical representation of classes of the material in test and training samples

Number of class	Characteristics of the material	Quantity in the test sample	Quantity in the training sample
1	Excellent material properties	32	150
2	Optimal material properties	24	94
3	Material with possible defects	32	100
4	Defective material	8	40

The Method 1 and the Method 2 are implemented in Python using libraries LIBSVM [21] and LIBLINEAR [22]. Visualization of the results of the used methods was conducted using the Orange Software [26].

The classification results were evaluated according to the formula:

The number of correctly classified vectors Accuracy =

The test sample size

The number of correctly classified vectors

⁼           96

Table 2, based on (1), presents the results of comparing both developed methods with existing ones. As can be seen from Table 2, the best results for solving the classification task by both developed methods were shown.

Table 2. Comparison of the accuracy for different methods

#	Method	Accuracy
1	Logistic Regression	63,54
2	SVC (RBF kernel)	63,54
3	Linear SVC	63,54
4	SVC (linear kernel)	76,04
5	Random Forest	93,75
6	Method from [9]	95,83
7	Method 2	95,83
8	Method 1	96,88

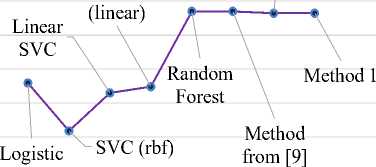
Fig.2 presents the results of comparing the accuracy of the work of all methods in training and testing modes. As can be seen from the graphs, the developed methods show a slight difference in the values of accuracy in both modes of operation. This testifies to the possibility of practical application of these methods for solving applied tasks of Material Science.

Fig.4 shows scatter plots of all investigated methods. As can be seen from Fig.4 (g, h, i) the best results are shown by the methods 6, 7, 8 from Table 2. It should be noted that besides the low accuracy of the work, methods 1, 2, 3 and 4 of Table 2 are identified samples of class 4 as representatives of class 1 or 2 (Fig.4 (b, c, e, f)).

This increases the likelihood of the creation of a medical implant part from a material that is generally not recommended for use (a class 4 from Table 1). The risk of such a situation leads to a number of negative consequences, and such methods are not recommended for use in solving the task.

An important point when applying machine learning methods is the time of their work. In addition to ensuring high accuracy, similar methods should provide a high speed in training mode о 103

и 93

о

d

Method 2

SVC

Regression

0246 Methods

8             10

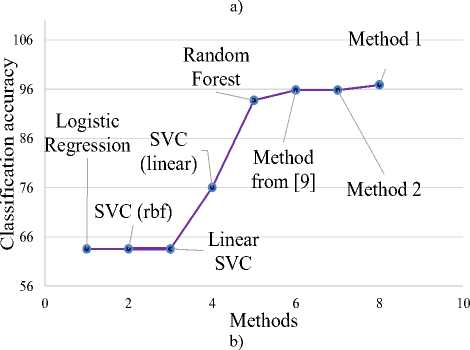
Fig.2. Visual comparison of the classification accuracy for the developed methods with the existing ones: a) in training mode; b) in test mode.

In this paper, the investigated of the comparing the results of the training time for all methods was conducted. In Fig. 3 the results of the conducted experiments are presented. As can be seen from Fig. 3, the Method 1

(Linear SVC + Wiener Polynomial)) shows a very small training time. However, compared with the base Linear SVC, the proposed method is working is 1.7 times slower. This is due to the implementation of step 1 of the method. It involves the representation of input data in the form of members of the Wiener polynomial, which substantially increases the dimension of each input vector. That is why the length of the training procedures are increasing

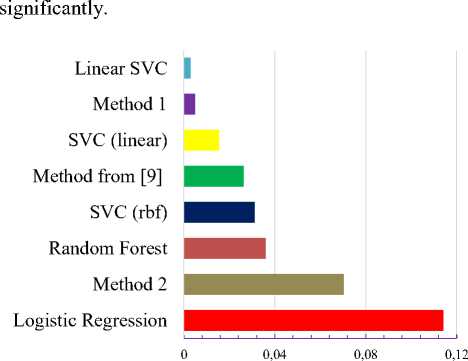
Fig.3. Comparison of training time of the developed machine leaning methods with existing ones.

Nevertheless, comparing the developed method with the method of [9] shows an increase in speed more than 7 times with the same values in accuracy. Regarding the Method 2 (SVC (linear kernel) + Wiener Polynomial). It increases the training time compared to the basic SVC (linear kernel).

However, the advantage of the proposed method is the high accuracy of the solution for the classification task, which is 32.29% higher than the accuracy of the basic method. In addition, the Method 2 is worse (the classification accuracy) only compared to the Method 1 from all investigation methods in this paper.

Based on the obtained results (the accuracy and speed) of the proposed methods, it can be asserted that:

– the developed methods show a high accuracy of the task of identifying the material class, which determines the possibility of their practical use for solving such tasks;

– the Method 2 should be used for solving classification tasks in the Material Science field in case that doesn’t impose restrictions for their training time;

– the Method 1 shows the greatest accuracy of the solution of the classification task among all the considered ones. It only shows a slightly worse result compared to the basic method for the performance of the training procedure;

– based on the accuracy and speed of the Method 1 work, it can be used to solve applied classification tasks in the case of large dimensions of the input data;

– the proposed approach shows a high accuracy of calculating the Wiener polynomial coefficients, which enables its application in the fields of medicine[27], education [28], image processing

[29], in particular, for solving tasks of both classification and regression.

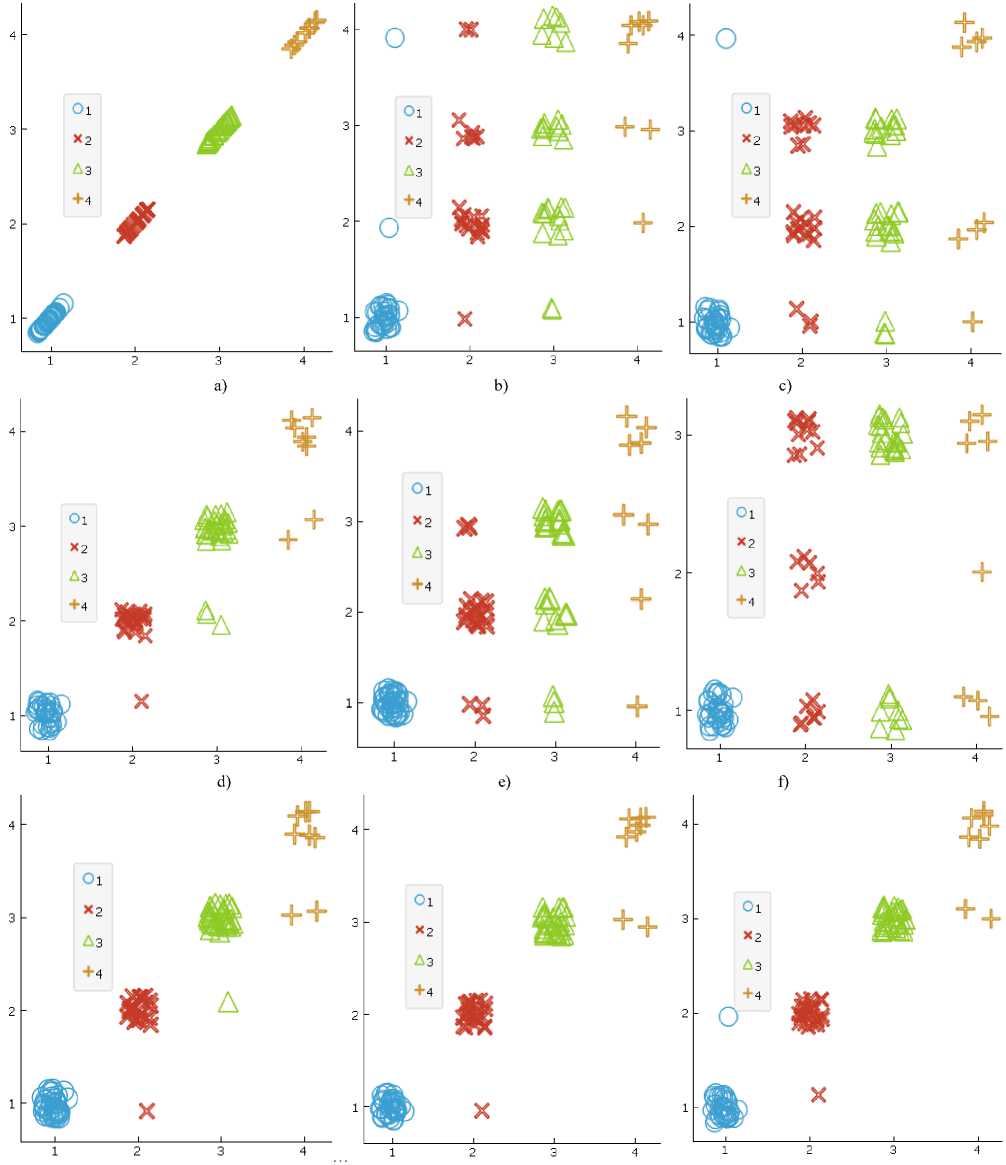
g)

h)

i)

Fig.4. Visual comparison of the developed methods with existing ones. On the x-axis there are true values, on the y-axis there are obtained values by one of the methods: a) Initial status (ideal variant); b) Logistic Regression; c) Linear SVC; d) Random Forest; e) SVC (linear); f) SVC (rbf); g) Method from [9] (Random Forest + Wiener Polynomial); h) Linear SVC + Wiener Polynomial ; i) SVC (linear) + Wiener Polynomial.

• V.    Appendix A Parameters of the Methods

The basic parameters of the developed methods and the methods that were used for comparison can be seen in Table 3 [18, 30].

Table 3. Basic parameters of the methods

#	Method	Parameters
1	Logistic Regression	multi_class : ‘multinomial’; class_weight : ‘balanced’; solver : ‘lbfgs’.
2	SVC with RBF kernel (C-Support Vector Classification)	coef0 : 0.0; shrinking : True; C : 0.3; kernel : 'rbf'; degree : 3; gamma : 'auto'; class_weight : None; verbose : False; max_iter : -1; probability : False; tol : 0.001; cache_size : 200; decision_function_shape : 'ovr'; random_state : None
3	Linear SVC (Linear Support Vector Classification)	tol : 0.0001; C : 1.0; multi_class : 'ovr'; penalty : 'l2'; loss : 'squared_hinge'; dual : True; verbose : 0; random_state : None; max_iter : 10; fit_intercept : True; intercept_scaling : 1; class_weight : None.
4	SVC with linear kernel (C-Support Vector Classification)	kernel : 'linear'; other parameters are the same as in method 2
5	Random Forest	min_samples_split : 2; n_estimators : 10; random_state : 0; max_depth : None.
6	Method from [5]	Wiener polynomial : second degree; n_estimators : 9; other parameters are the same as in method 5
7	Linear SVC + Wiener Polynomial	Wiener polynomial : second degree; other parameters are the same as in method 3
8	SVC (linear) + Wiener Polynomial	Wiener polynomial : second degree; other parameters are the same as in method 4

• VI.    Conclusions

The paper describes two developed methods for the titanium alloys classification for medical purposes. They are based on combining of the Wiener polynomial and SVM. To implement the machine learning procedures, two similar implementations of the SVM method from different Python libraries were used.

The experimentally established effectiveness of the developed methods that provide the highest classification accuracy was compared with existing methods.The SVM’s training time was evaluated experimentally. The Method 1 (Linear SVC + Wiener Polynomial) has been found to provide a high speed and the highest accuracy.

That is why it can be used for solving applied classification tasks in case of the necessity of taking into account the functional properties of structural materials. These properties, in turn, depend on the chemical composition and microstructure of the choosen materials, which determines the large dimensions of the input data (Big Data processing).

It has been found that the Method 2 (SVC (linear kernel) + Wiener Polynomial) should be used for solving classification tasks in cases that do not impose restrictions for the training time.

• VII.    Acknowledgment

The authors would like to thank to Dr. Ihor Lemishka and Dr. Volodymyr Kulyk and senior researcher Anatolii Kovalchuk for the assistance with data preparation and participation in the development of Artificial Intelligence methods for solving applied tasks of Material Science.