The Complement of Normal Fuzzy Numbers: An Exposition

Published Online July 2013 in MECS

In the theory of fuzzy set as proposed by Zadeh [1], the two fundamental laws of Boolean algebra- the law of contradiction AA^c = ∅ , the universal set and the law of excluded middle AA^c =Ω , the empty set are not satisfied. In other words, it is possible for an element to partially belong to both a fuzzy set and set’s complement. The reason behind such a claim can be contributed to the fact that the complement A^c of the fuzzy set a is defined by the membership function

µAc(x) =1-µA(x),∀x∈Ω (1)

Using this definition of complementation, various theories have been developed all of which cannot be covered in this article. Here for illustration, we would discuss a few: cardinality, entropy, subsethood theorem and also in the case of fuzzy matrices. Similarly, we have found some drawbacks in the results obtained by various researchers working in the field of probabilitypossibility consistency.

The main purpose of this article is to convey that the aforementioned way of representing the complement of fuzzy sets as well as the consistency principles established so far can never give us the desired result. It seems that the existing definitions were not proposed within appropriate mathematical frameworks. In most cases of practical significance, it is desirable to consider an additional requirement for defining fuzzy complement to make it logical. This realization led Baruah ([2], [3], [4]), to propose that the most desirable requirement in defining the correct complementation is the use of reference function and also the existence of two laws of randomness is required to define a law of fuzziness.

The rest of the article is organized as follows: Section II deals with the new definition of complementation of fuzzy sets.Section III deals with some existing definitions and theories of fuzzy sets and their newly proposed definitions. Section IV deals with the addition, multiplication and trace of fuzzy matrices.Section V deals with the determinant and adjoint of fuzzy matrices. Finally, section VI gives the conclusions.

Before embarking in deeper study on various aforementioned theories of fuzzy sets, let us reflect a little on the new definition of fuzzy sets put forward by Baruah. This can be described as follows:

• II.    Baruah’s Definition of Complementation of Fuzzy Sets

A possible justification of this may be as follows: If a glass is half full then the empty portion will be measured from the portion which is filled. From the standpoint of the new definition of complementation, the point from which the empty portion of the glass stats would have to be considered as the reference function.

As an illustration of the above formalization, we are going to mention the following few lines.

Say,

A ( µ ₁, µ ₂) = { x , µ ₁( x ), µ ₂( x ), x ∈ Ω }         (2)

and

B ( µ ₃, µ ₄) = { x , µ ₃( x ), µ ₄( x ), x ∈ Ω }         (3)

be two fuzzy sets defined in our way.

Then the operations of intersection and union defined naturally as

A ( µ ₁ , µ ₂ )   B ( µ ₃ , µ ₄ )

= { x ,min( µ ₁( x ), µ ₃( x )),                      (4)

max(µ2(x),µ4(x))} and

A ( µ ₁ , µ ₂ )   B ( µ ₃ , µ ₄ )

= { x ,max( µ ₁( x ), µ ₃( x )),                     (5)

min( µ ₂( x ), µ ₄( x ))}

For usual fuzzy sets we are to consider

µ ₂( x ) = µ ₄( x ) = 0

For two fuzzy sets

A(µ, 0) = {x,µ(x),0,x ∈ Ω} and

B(1,µ) = {x,1, µ(x), x ∈Ω} defined over the same universe Ω , we would have

A ( µ ,0) n B (1, µ ) = { x , min( µ ( x ),1), max(0, µ ( x ))}          (6)

= {x,1, 0, x∈ Ω} which is nothing but the null set φ .

A ( µ ,0)и B (1, µ ) = { x , max( µ ( x ),1), min(0, µ ( x ))}         (7)

= {x,1, µ(x), x ∈ Ω} which is the universal set.

In other words, B (1, µ ) is the complement of A ( µ ,0) in the sense of classical set theory.

In accordance with the process discussed above, a fuzzy set defined by

A = {x, µ(x),x ∈ Ω} would be defined in this way as

A = {x, µ(x), 0, x ∈ Ω} so that the complement would become

Ac = {x,1, µ(x), x ∈ Ω}

This concept can be visualized from the following diagram

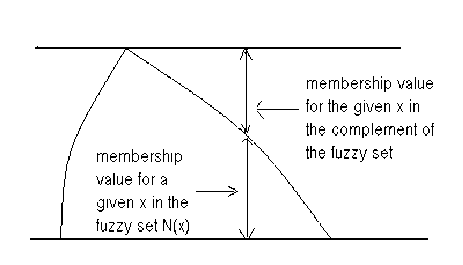
Fig. 1: New definition of complementation of fuzzy sets

From this definition of complementation, we would like to say that the results obtained by using the existing definition of complementation would not be logically satisfying. Further it is important to note here that using the new definition of complementation; we see that unlike classical sets fuzzy sets also satisfy the excluded middle laws.

Symbolically these can be expressed as

AA^c = ∅ , the null set and

AA^c =Ω , the universal set

It is important to mention here that the new definition of complementation does satisfy almost all the properties of fuzzy sets except the two most debatable laws. As we see that the new definition performs precisely as the corresponding operation on crisp sets, it in fact challenges the most sacred elements of the foundation- fuzzy sets violate the excluded middle laws, which has been taken for granted from the inception of the theory and viewed as inviolable.

Application of the existing definition of fuzzy sets is quite extensive particularly in those endeavours concerned with cardinality, entropy, geometrical representation of fuzzy sets, subsethood as well as fuzzy matrices. The motivation for the application of the new definition lies in the need to handle some illogical conclusions.

So in this article, we would like to focus our attention to some of the theories of fuzzy sets with special reference to the cardinality, entropy, subsethood and fuzzy matrices. Let us have a brief look at these in the following sections.

• III.    Some Results of Fuzzy Sets

• 3.1    Fuzzy Sets and Boolean Algebra

  The mathematical system developed by George Boole (1815-1864) in an attempt to give symbolic form to Aristotle’s system of logic is known as Boolean algebra. Boolean algebra can be obtained as a set of subsets A, B, C⊆Ω which satisfies the following properties:

This section deals with some existing definitions and theories of fuzzy sets and their new definitions proposed which are in accordance with the theories developed by Baruah as the case may be.

1.    AUB = BUA,A^B = BAA 2.    AU (BUQ = (AUB )U C 3.    AA(BAG) = (AAB)AC 4.    AU(AAB) = A,AA(AUB) = A 5.    AA(BUG) = (AAB)U(AAC) 6.    AU(BAG) = (AUB)A(AUG) 7. (AAB)C = Acw 8.  (AUB)c = Ac V\BC 9.  (Ac)c = A 10.    APlAC = p,AUAC = Q

It can be easily verified that the properties for Boolean algebra are satisfied by fuzzy sets also, Dhar [5] if the complementation is defined on the basis of reference function.

fuzzy set theory. Since an element can partially belong to a fuzzy set, a natural generalization of the classical notion of cardinality is to weigh each element by its membership degree, which gives us the following formula for cardinality of a fuzzy set. There are several approaches to the cardinality of fuzzy sets. One group of them had constructive approaches. Following these approaches, we get a single number or alternatively a fuzzy set as cardinality of fuzzy set. The first concept of this kind was proposed and discussed in De Luca and Termini [6]. In many applications, one prefers a simple scalar approximation of cardinality of a fuzzy set. Scalar cardinality of a fuzzy set is the sum of the membership values of all elements of the fuzzy set. In similar way fuzzy cardinalities of a fuzzy set that associate to any fuzzy set, a convex fuzzy natural number. But fuzzy cardinality of fuzzy sets is beyond the scope of this article. The scalar cardinality of a fuzzy set A is defined as follows:

I    A = 2 BA(ХД x e^                (11)

this A is called the sigma- count of A.

It is important to mention here that since we would like to define fuzzy sets with the help of two functions such as fuzzy membership function and fuzzy membership value. In parallel with what had been done for cardinalities of fuzzy sets, we shall define the cardinality of a fuzzy set A as:

IA = card(A) = ^{B2( x) - B1( x)}, x e Q

It can be easily seen that this new definition of cardinality satisfy the properties which were set for the existing definition, Dhar [7].

• 3.2.1    Properties of cardinality of fuzzy sets

• 3.2    Cardinality of Fuzzy Sets

The below mentioned properties are observed to hold for both usual fuzzy sets and their complements.

Property 1

If Ac c Bc then ^ count(Ac) c ^ count(Bc)

In fuzzy set theory, we can see the use of the term cardinality which is most commonly used concept in many areas. Cardinality belongs to most important and elementary characteristics of a set. The cardinality of a crisp set is the number of elements in the set. Using fuzzy sets which are many-valued generalization of sets, one likes to have for them analogus characteristics. The concept of cardinality of fuzzy sets received a lot of attention from the researchers from the beginning of

Property 2

^ Count (Ac) + ^ Count (Bc )=

2 Count(Ac U Bc) + ^ Count(Ac A Bc)

Property 3

∑count(AcBc)

≤ min(∑count(Ac),∑count(Bc)

≤ max(∑count(Ac),∑count(Bc))

∑count(AcBc)

• 3.3    Entropy of Fuzzy Sets

Fuzzy entropy is the measurement of fuzziness of fuzzy sets, and thus has an important position in fuzzy systems such as fuzzy decision making systems, fuzzy control systems, fuzzy neural network systems, and fuzzy management information systems.

Kosko ([8], [9]) has defined the entropy of a fuzzy set A as:

E ( A ) =	AAc
	AAc

where

I AA^c I and I AA^c I

denote the cardinalities of

the sets AA^c and AA^c .

De Luca and Termini [6] suggested as a measure of fuzziness the “entropy” of a fuzzy set, which they defined as follows:

The entropy as a measure of fuzzy set

A = {x, µ (x), x ∈ Ω} is defined as

D(A)=H(A)+H(Ac)                 (14)

H(A)=-K∑µA(xi)InµA(xi)           (15)

j = 1

where n is the number of elements in the support of A and K is a positive constant.

Yager [10] argued that the measure of fuzziness should be dependent on the relationship between the fuzzy set A and its complement Ac .Then he suggested that the measure of fuzziness should be defined as the lack of distinction between a and its complement Ac . Yager defined a measure of fuzziness of A in the following manner:

f p ( A ) = 1 -

D p ( A , A^c ) isup p ( A )5

where n1

Dp(A,Ac)=[∑µA(xi)-µAc(xi)]p      (17)

i = 1

where A^c stands for the complement of the set A.

Soyer, Kabak and Asan [17], while finding fuzzy based methodology for value and culture assessement, used a non-probabilistic entropy measure introduced by Shang and Jiang [18], which is as follows

H(C)=1∑n µCC(xi) (18) ni=1 µCC(xi)

Where n denotes the number of values in the culture type, x is the average of values of all respondents’s judgement for a given value i, and µ ( x ) denotes the degree of belongingness of the value i to the culture C and is the complement of the set C. Here also, we would like to discard the result obtained with this formula due to the same reason.

Again Fan and Liang [19], introduced the concept of σ -entropy as

If e is the σ - entropy, then

e(A)=e(Ac)=e(A Ac)=e(A Ac) (19)

Now if the results of the new definition of complemention are used, then we arrive at a very peculiar result in the form

e(Ω) =e(φ) (20)

• 3.3.1    New definition of entropy of fuzzy numbers

• 3.3.2    Properties of entropy of fuzzy numbers

Keeping in view of the original definition of Shannon’s entropy which is defined as:

H ( p ) =-∑ p_iInp_i i =1, 2, n.              (21)

i where p , p ,......., p denotes the probabilities of n events, fuzzy entropy too can be defined by using the Randomness-Fuzziness Consistency Principle defined by Baruah [21]

Accordingly, the left reference function of a normal fuzzy number which is nothing but a distribution function, would lead to entropy E . In a similar manner, the right reference function of the normal fuzzy number, which is nothing but a complementary distribution function, would lead to another entropy E .The pair [ E , E ] found can rightly be called fuzzy entropy in the classical sense of defining Shannon’s entropy for a discrete law of randomness. Discretizing a law of randomness for a continuous variable should not be of much problem, which in turn can be used to define fuzzy entropy [ E , E ] , where E and E are Shannon’s entropies for the left reference function and right reference function respectively. This was discussed in more details in Dhar [20]. Some properties of fuzzy entropy are observed which are the results of the new definition of entropy of fuzzy sets, Dhar [22] and these properties are listed below:

This subsection deals with some properties of entropy of fuzzy numbers. These are

Property1

Entropy of all triangular fuzzy numbers is the same for the same choice of the length of the interval.

Property2

Entropy of the sum of two fuzzy numbers A+B is the same as that of the numbers A and B for the same choice of intervals.

Property3

Entropy of the product of two fuzzy numbers AB is not the same as that of the numbers A and B for the same choice of intervals. The reason is that the product AB of two triangular fuzzy numbers is not a triangular fuzzy number.

It is important to note here the fact that if we consider non-triangular fuzzy numbers then the above mentioned properties donot hold.

• 3.4    Kosko’s Subsethood Measure of Fuzzy Sets

A fuzzy subsethood measure (also called a measure of inclusion) is a relation between fuzzy sets A and B which indicates the degree to which a certain fuzy set A is contained in another fuzzy set B. Fuzzy subsethood or fuzzy inclusion is an important concept in the field of fuzzy set theory. The first attempt to define fuzzy subsethood theory was made by Zadeh [1], which is discussed below

For two fuzzy sets A and B, the set A is said to be the subset of another set B if the membership values of the set A is less than or equal to the membership values of the set B.

That is to say, a fuzzy set A in the Universe U is a subset of another fuzzy set B if for every element x in U, its membership degree in A is less than or equal to the membership degree in B. This can formally be stated as

A⊆B⇒µA(x)≤µB(x) (22)

Kosko [9], criticizes the definition of fuzzy set containment given by Zadeh pointing out that if this inequality holds for all but just a few x, we can still consider A to be a subset of B to some degree.

I AB S(A,B)=

Again it is to be remembered that this measure of subsethood also lies between 0 and 1.

But here we would like to criticize this definition of subsethood for two reasons. Firstly, using this formula it was derived that AA^c is a subset of AA^c to some degree and considered this as the unique feature of fuzzy set theory. This is not desirable because in our case AA^c is the universal set and AA^c is the null set. Thus we can see here that the Universe of discourse can also become a subset of any of its own subset to some degree. This is not logical from our standpoints. This is also discussed in our previous work (see for example Dhar ([22]).

Another reason for which this subsethood measure can be criticized lies in the fact that there are some drawbacks in the geometrical representation of fuzzy sets also. Before proceeding further, let us have a look at the geometrical representation of fuzzy sets in short in the next section.

• 3.5    Geometrical Representation of Fuzzy Sets

Consider a universe of discourse containing two elements, U = {x, x^ } and a fuzzy set defined in that universe of discourse

1       3

A = {( X - ,-),( X 2 ,-)}

. Then

the point A can be represented as a point in two dimensional unit hypercube which is a square. This square represents all possible fuzzy sets of both elements; vertices of the square represent crisp set.

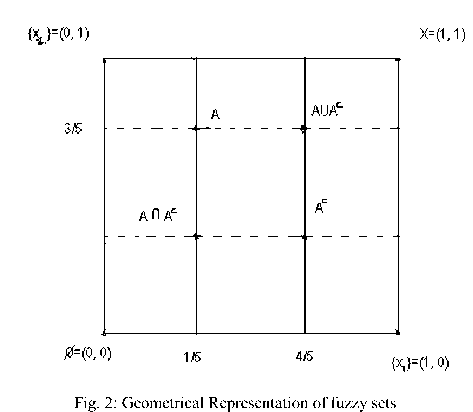
• 3.6    Measure of similarity between two fuzzy sets

The concept of similarity is a basic concept in human cognition. The fuzzy similarity measures introduce the notion of approximate equality (or similarity) between fuzzy sets. The similarity of fuzzy sets may vary from 0 which means completely distinct to 1 which means fuzzy sets are similar.There are many aspects of the concept of similarity.There are several similarity measures which have been proposed and used for varied purposes. Here, we shall discuss about the most common and well known similarity measure as proposed by Dubois and Prade [25] which is as follows:

AB

S ⁽ A , B )=Ы                 ¹²⁴¹

Again Kosko [26], defined the similarity measure which is based on n-dimensional unit hypercube concept in the following manner

AB

E ( A , B ) = AB                     ^<25)

Here it is important to mention here is that by using this definition of similarity we get a degree to which A is similar to A^c and in the same way AA^c is similar to AA^c . This is not desirable from our standpoints. Thus it may be concluded that this similarity measure between fuzzy sets cannot be accepted.

So in the cases where the complementation is involved, we would like to suggest the use of new definition of complemention of fuzzy sets on the basis of reference function. This would in fact produce two results which may be in form

• (i)    S ( A , A c ) = 0 and

• (ii)    s ( A D A c , A U A c ) = 0

But this representation is not logical from the view point of new definition of complementation of fuzzy sets, Dhar ([23] & [24]). The reason behind such a claim can be had from the fact that the points AA^c and AA^c in the figure coincides with the corner points ф and X respectively from the standpoint of the new definition. Thus we can say that the geometrical base of the subsethood theorem is also not so strong to support the proposal. Then the only way to get rid of such controversial result is the use of reference function in defining complementation.

• IV. Fuzzy Matrices

It is well known that the matrix formulation of a mathematical formulae gives extra advantage to handle/study the problem.When the problems are not solved by classical matrices, the concept of fuzzy matrices are used. Matrices with entries in [0, 1] and matrix operation defined by fuzzy logical operations are called fuzzy matrices. All fuzzy matrices are matrices but every matrix is not a fuzzy matrix. Fuzzy matrices were introduced first time by Thomson who discussed the convergence of powers of fuzzy matrices. Fuzzy matrix has been proposed to represent fuzzy relation in a system based on fuzzy set theory. Just as a classical relation can be viewed as a set, fuzzy relation can also be viewed as a fuzzy subset.

In this article, we would like to suggest a fuzzy matrix representation based on reference function. Furthermore, new definitions for trace of a fuzzy matrix, determinant and adjoint of fuzzy matrices along with some properties associated with this definition is also suggested .It is important to mention here the fact that we would discuss about these in brief as these have been discussed in more details in our previous work (see for example Dhar ([26]). Let us have the following few lines as support of the statement.

Accordingly, for the a square fuzzy matrix of order 3

^ a1 b1 c1' B = a2 b2 c2 .a 3 b3 c 3 v would be represented as in the following way according to Dhar [27]

	' ( a 1 ,0)	( b 1 ,0)	( C 1 ,0) '
B =	( a 2 ,0)	( b 2 ,0)	( C 2 ,0)
	v ( a 3 ,0)	( b 3 ,0)	( c 3 ,0)V

A + B = {max(a,, by ), min(r, r' )}

where a stands for the membership function of the fuzzy matrix A for the ith row and jth column and r is the corresponding reference function and b stands for the membership function of the fuzzy matrix B for the ith row and jth column where r ‘ represents the corresponding reference function.

(ii) Multiplication of two square fuzzy matrices

The multiplication of two fuzzy matrices A and B, will be defined and can be represented in the following form:

AB = {max min( ay, byt), min max( r, r.‘}

provided the matrices are conformable for multiplication and the symbols have their meaning same as that discussed earlier.

And then the complement of the above matrix will be written as

Bc

(1, a 1 )	(1, b 1 )	(1, c 1 )
(1, a 2 )	(1, b 2 )	(1, c 2 )
(1, a 3 )	(1, b 3 )	(1, c 3 )

That is to say that a fuzzy matrix A = [ a_y ] would have to be represented as A = [( a_y , 0)] and then its complement A c would take the form A c = [(1, a ^ )]

Here we are interested in discussing the complement of a fuzzy matrix is due to the fact that it is often used to analyze the complement nature of any system. For example, if a fuzzy matrix A represents the crowdness of a network at a particular time period, then the complement of that matrix denote the clearness of the network during the same time period. It is for this reason, we have mentioned about the complement of a fuzzy matrix along with the usual fuzzy matrix.

After defining fuzzy matrices in the above mentioned way, the addition and multiplication of matrices are also defined, Dhar [27]. Let us have a brief look at these in the following:

(i) Addition of two square fuzzy matrices

If A and B be two matrices of same order then their addition can be defined as follows

• 4.1    Trace of a Matrix

• 4.2    Properties of Trace of a Matrix

The trace of a fuzzy matrix is defined as

Let A be a square matrix of order n. Then the trace of the matrix A is denoted by tr A and is defined as trA = (max ^, min ru)

where Ц^ stands for the membership functions lying along the principal diagonal and r refers to the refence function of the corresponding membership functions.

The following properties can be easily verified

Let A and B be two fuzzy square matrices each of order n and X be any scalar such that 0 <  X <  1 . Then

i.   tr (A + B) = trA + trB ii.   tr (XA) = XtrA iii.    trA = trA , where A is the transpose of A. V.    Determinant and Adjoint of Square Fuzzy Matrices

On the basis of representation of fuzzy matrices in terms of reference function, the determinant and adjoint of fuzzy matrices are also found out, Dhar([27])

• 5.1    Determinant of a Square Fuzzy Matrix

The determinant of the above square fuzzy matrix would be denoted by

(a1,0) (b1,0) (c1,0) (a2,0) (b2,0) (c2,0) (a3,0) (b3,0) (c3,0) and this would be defined as

(b2,0)  (c2,0)

(b3,0)  (c3,0)

+ ( b 1 ,0)	( a ,0) ( a 3,0)	( c 2 ,0) ( c 3 ,0)
	( a ,0)	( b 2 ,0)
+ ( c 1, 0)
	( a 3 ,0)	( b 3 ,0)

= (ax,0)[max{min(b,c3), min(b3,c2)}, min {max (0,0), max (0,0)}    (29)

+ (b, 0)[max{min(a2, c3) min(a3, c2)}, min {max (0,0), max (0,0)}

+ (c,0)[max{min(a2,b3) min(a3, b2)}, min {max (0,0), max (0,0)}.

Proceeding similarly, we can find the value of the determinant of the complement of any square matrix.

The following properties of determinant can be easily verified if we represent fuzzy matrices on the basis of reference function. It is important to note here that the properties hold for both usual fuzzy matrix and complement of a fuzzy matrix.

• 5.1.1    Properties of determinant of a square fuzzy matrix

Property1

If the determinant is expanded along any row or column then the value remains the same

Property2

If the rows and columns are interchanged then the value of the determinant remains the same.

If any two rows or any two columns are interchanged in their positions, the value of the determinant remains the same.

Property3

If the elements in a row (column) are all zero, the value of the determinant is also zero.

Property4

If A and B be two square fuzzy matrices of same order then the following property will hold

det( AB) = det A det B

Property5

If the elements of any row (or column) of a determinant are added to the corresponding elements of another row (or column), the value of the determinant thus obtained is equal to the value of the original determinant.

• 5.2    Adjoint of a Square Fuzzy Matrix

Let A = [ a ] be any matrix which is represented as A = [( a^ , 0)] in our way. Then B = [ b ]_яхя where ^by = A y | ^and| j is the determinant of the square fuzzy matrix of order (n-1) obtained from a square fuzzy matrix A of order n by deleting row and column i. Then the matrix B is defined as the adjoint of the matrix A. It is to be noted here that the adjoint of a matrix is of the same order as that of the given matrix.

Then the adjoint of the matrix B would symbolically be represented as

' ( b 11 ,0) adjB = ( b _{2 p}0)

. ( b 31 ,0)

(b12,0)   (b13,0)

(b22,0)  (b23,0)

( b32,0)   ( Ьзз,О) V

If the complement of the matrix is to be considered then we are required to proceed similarly by defining the complement of the given matrix.

Then the following properties are observed to hold both for usual fuzzy matrix and complement of fuzzy matrix, Dhar [28]

• 5.2.1    Properties of adjoint of fuzzy matrices Property1

If A be a fuzzy square matrix, then we get A ( adjA ) ^ ( adjA ) A

Property2

If A be a fuzzy square matrix, then det ( adjA ) = det A

Property3

If A be a fuzzy square matrix, we shall show that det A ( adjA ) = det A = det( adjA ) A

Property4

If A and B be fuzzy square matrices then adj ( AB ) = adjAadjB

• VI. Conclusions

In this article, new definition of complementation of fuzzy sets is suggested because there are some drawbacks in the existing definition of complementation. The main purpose of this article is to revisit and comment on some of the results associated with the existing definition of complementation of fuzzy sets.These results are discussed from the standpoints of the new definition of complementation of fuzzy sets on the basis of reference function and some new definitions are put forward whenever possible.It is expected that these new definitions would be able to remove the drawbacks that currently exist. That is to say that the basic disadvantages of the previous definition have been overcome with this new definition of complementation of fuzzy sets.

Acknowledgements

The authors would like to thank the anonymous reviewers for their careful reading of this article and for their helpful comments.