The compression algorithm of hyperspectral aerospace images with use of mathematical processing and intrabands correlation

technology of finding a high correlation of channels groups of hyperspectral data cube on the basis of the group of squared correlation. The disadvantage of such approaches is the time required to compress and restore the image, which depends on calculation of spectral correlation matrix, and also the proposed schemes produce an average compression ratio which reaches only 3,2.

In the article [5, 9] it is proposed to use randomized methods for reducing dimensionality for effective coverage of the correlation structure and encoding the part remained, and for ensuring lossless compression. This approach is used especially for the efficient lossless on-board compression, data transmission and reconstruction of HSI data. One of the problems for the residual encoding is the speed. In this regard, a recent encoding development showed a throughput which reached 75 GB/s on the GPU. In the works [6, 8, 10] there were resolved two important issues related to the storage and transmission of hyperspectral images, considering the lossless compression models. Also there was studied the SLSQ algorithm and its condition in modern lossless compression schemes, and this algorithm is suitable for on-board implementation. Also two approaches to improve the SLSQ compression are considered. The first approach is a pre-processing of the scheme which orders the channels before compressing a hyperspectral image, also we studied the correlation between the channels. The second approach is based on the pre-processing time and this individualizes a set of channels which are better compressed with two-dimensional inter-channel predictor instead of threedimensional SLSQ. The main idea of the approach is determined by the fact that the SLSQ NR-groups of the algorithm are not effective, reaching a compression degree of 3,3.

Approaches of lossless compression are considered by most researchers, because the lossless algorithms are effective as the information is important in many fields such as RSE environmental protection, the earth’s surface monitoring, military purposes, etc.

Based on the conducted studies and the above approaches to algorithms and methods of compression of hyperspectral AI it can be assumed that these disadvantages stimulate intensive researches aimed at finding new effective solutions which provide high rates of compression degrees and calculators for processing hyperspectral AI, as well as the development (modification) of new algorithmic software.

One of the perspective ways of solving the problems of hyperspectral AI compression is the development of algorithmic software with the new methodology of accounting an inter-channel correlation and creating new algorithms. There are some works devoted to this field [11-13], which suggest the need to develop new algorithms and improve existing ones in lossless compression for hyperspectral AI. There are also the developments in the works [14, 15], where preparatory lossy and lossless processing of algorithms is proposed. In this regard, this article proposes some modifications and new stages of the algorithm of lossless compression based on the conducted researches.

Stages of the compression algorithm

There has been suggested the algorithm with interchannel finding of the best channel of intrabands correlation and the use of indexed lossless encoding, which allows to reduce the dimensions of the image channels and to convert them before compression. As a result, the compression degree of the channels of hyperspectral AI processed by well-known statistical algorithms has become much higher. Also some results of study of the compression degree in the number of channel groups were revealed.

Set of the algorithm stages:

• 1)    the calculation of the correlation matrix between AI channels, finding the best correlated channel pairs in all possible combinations, the subtraction of the best pairs of AI channels;

• 2)    the indexed encoding is the encoding in which the range of hyperspectral data ranges from 0 to 255 bytes, this proposed algorithm reduces the range which varies from 0 to 68. The index is the number of the position of the data range value of additive RGB color model. The effectiveness of indexing and increasing the degree of compression is that the indices are in a small range, so they are well-compressed by entropy encoding;

• 3)    the statistical compression algorithm.

Stages of the algorithm.

Stage 1. Consideration of intrabands correlation.

Calculating the correlation value (intrabands dependence) between hyperspectral AI channels allows to reduce the data range, so fewer number of rates for their storage is needed. The best correlated channel should be found. Then the consideration of intrabands correlation between the selected channels of hyperspectral aerospace image by selecting the correlation value and forming the deviations (differences) of the original data should be taken into account.

For a detailed description of the first stage it is necessary to consider the following objects:

• –    the original image – matrix of the image values I [ m,n,k ], where m,n,k are the indices of lines, columns and channels of the original image, m = 1,2,..., M, n = 1,2,..., N, k = 1,2,..., K ;

• –    A [ k ] – the array for values storage when calculating the mathematical expectation of each channel;

• –    I’ [ m,n,k ] – the array for placing differences (deviations) values between the value of the mathematical expectation A [ k ] and I [ m,n,k ];

• –    C [ k ] – the array for storage of correlation values cor between the adjacent ranges (channels);

• –    K best is the best correlated channel;

• –    I” [ m,n,k ] – the array for placing differences (deviations) values between the channels I’ [ m,n,k ] and I [ m,n,k ];

Step 1. To calculate the mathematical expectation of each channel of the original image I [ m,n,k ] and place the values in the array A [ k ].

Step 2. To search the channels I [m,n,k] in all I [ m,n,k+1 ] and place in the array K best .

Step 3. To calculate the correlation cor (on the basis of A [ k ] and I [ m,n,k ]) for each pair from all available К channels of the original image I [ m,n,k ]. The result should be placed in C [ k ], k =1,2,..., K -1.

• 2 (I'[m,n,k]-A[k])X(I'[m,n,k-1]-A[k-1])

C [ k ]         m , n                                                                          _.

(I'[m,n,k]-A[k])     (I'[m,n,k-1]-A[k-1])2 .

m , n                                        m , n

Step 4. To calculate the differences (on the basis of A [ k ], K best and I [ m,n,k ]) between the actual values of I [ m,n,k ] and the mathematical expectation for each pair from all available K and K best channels of the original image. The result should be placed in I ’[ m , n , k ], k =1,2,…, K- 1. I' [ m , n , k ] _{m , n} ( I [ m,n,k ]- A [ k ]).

Step 5. To calculate the difference (on the basis of A [ k ] and C [ k ]) between the elements I’ [ m,n,k ] and the corresponding values of the original image I [ m , n , k ] in each from K channels

where C[k] 0, I'[m,n,k]-I[m,n,k-1]

I '[ m,n,k ]                                              . for m = 1. M , n = 1. N The result should be

where C[k] 0, I[m,n,k]

placed in I’’ [ m , n , k ].

As a result the array I” [ m,n,k ] based on the intrabands correlation values C [ k ] is formed.

The subtraction (differential conversion) gives a special advantage in the compression of hyperspectral aerospace images, and also takes into account such spectral characteristics as high interchannel correlation, that increases the compression degree comparing with the universal algorithms which do not consider AI features.

Stage 2. The indexed encoding.

The efficiency of the algorithm is the range of hyperspectral data varied in a certain range of possible values using additional one-dimensional data structures. In data structures the values are kept in the form of indices. Index is the position number of the data range value of hyperspectral AI channel. Then, non-repeating indices of the values of auxiliary data structures are kept instead of the original values of hyperspectral aerospace images.

The formation of the new original data structure by the subtraction of the sequence unit of the values we receive a diminished image thus internal block elements of the image channel are defined, this creates three main data structures.

Let us consider the proposed algorithm with the help of the above stage. We introduce the following objects for consideration:

• –    auxiliary data structures (ADS) to obtain one-dimensional arrays of each image channel I [ m,n,k ] = I 1 [ m , n , k ], I [ m , n , k ] = I 2 [ m , n , k ], I [ m , n , k ] = I 3 [ m , n , k ], where 1-3 are ADS numbers;

• –    I [ k ] is the array to place the unique indices values of the pixels for each channel I [ m , n , k ] and ADS;

  – original indices I 1 [ m , n , k ], I 2 [ m , n , k ], I 3 [ m , n , k ], I 1 ’ [ m , n , k ], I 2 ’ [ m , n , k ], I 3 ’ [ m , n , k ].

Step 1. Convert hyperspectral AI channel into ADS I [ m , n , k ] = I 1 [ m , n , k ], I [ m , n , k ] = I 2 [ m , n , k ], I [ m , n , k ] = I 3 [ m , n , k ] corresponding to the values of the original image I [ m , n , k ] in the blocks. The result should be put in the arrays I’ [ m , n , k ].

Step 2. Form the arrays I’ [ m , n , k ] based on the auxiliary structures by replacing for each I 1 [ m , n , k ],

I ₁[ m , n , k ] I ₂[ m , n , k ] .

I ₃ [ m , n , k ]

I 2 [ m , n , k ], I 3 [ m , n , k ]. The result is put into the arrays: I'' [ m , n , k ]: I" [ m , n , k ]

Step 3. Form one-dimensional arrays of the original indices values I [ k ] on the basis of arrays I'' [ m , n , k ] G I ₁

I’’ [ m , n , k ] and ADS. The result is put in I [ k ]: I [ k ]: I [ k ]

I'' [ m , n , k ] G I

I'' [ m , n , k ] G I

In the result, there has been formed the array I [ k ] considering the formed array I” [ m,n,k ] and intrabands correlation C [ k ].

The advantage of the proposed algorithm is that the indices are in a small range, due to this they are well-compressed by entropy encoding and standard compression algorithms.

Stage 3. Compression using a well-known arithmetic encoding.

Test hyperspectral data

To determine the effectiveness of the proposed algorithm in terms of compression degree, and also the limits of its applicability there have been conducted the experiments on hyperspectral AI (RSE Aviris). The AVIRIS system ( Airborne Visible/Infrared Imaging Spectrometer ) provides simultaneous adoption of the 224 spectral images with a wave length between 400 nm and 2500 nm. Also there has been done the comparison of the proposed algorithm with experimental results obtained for universal archivers ( WinRar , WinZip and Lossles JPEG 2000 compressor) compression algorithms using an extension of JPEG compression standard, which is widely used in the commercial processing of RSE data. The experiments were done on a PC with IntelCore i5, 2.29 GHz and RAM of 4 GB with OS Windows 8.1 (Table).

Table. Characteristics of test hyperspectral AI

Channels number	Image size	Size(byte)	Channels number	Image size	Size(byte)
100	50*50	1081600	200	50*50	2163200
100	100*100	4080400	200	100*100	8160800
100	200*200	16160400	200	200*200	32320800
100	300*300	36240400	200	300*300	72480800
100	400*400	64320400	200	400*400	128640800
100	614*512	125747200	200	614*512	251494400
150	50*50	1622400	224	50*50	2421632
150	100*100	6120600	224	100*100	9140096
150	200*200	24240600	224	200*200	36199296
150	300*300	54360600	224	300*300	81178496
150	400*400	96480600	224	400*400	144077696
150	614*512	188620800	224	614*512	281673728

The results of the experiments

The Fig. 1 shows the compression algorithms when varying the number of channels and the geometric size (50×50) in comparison with the universal archivers Winrar, 7Z, and JPEG Lossless . Indicators of compression degree D are 25% higher than universal algorithms through searching the main channel, which determines the priority of channels compression and taking into account interchannel correlation, indexed encoding.

To improve the efficiency of the algorithm, the experiments on the following parameters were done:

• 1)    Cor – the given correlation value;

• 2)    N – the number of AI channels group;

• 3)    R – the size of AI channels;

• 4)    K – the number of channels in the group N .

Fig. 2 shows that the indicators of the compression algorithm degree in R are higher in the compression degree than archivers WinRar , 7Z , and JPEG Lossless more than 80%.

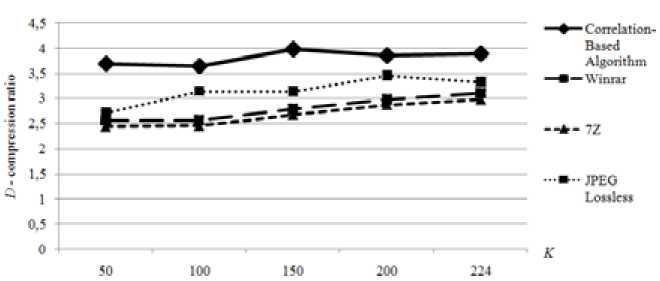
Fig. 1. Lossless compression algorithm according to K

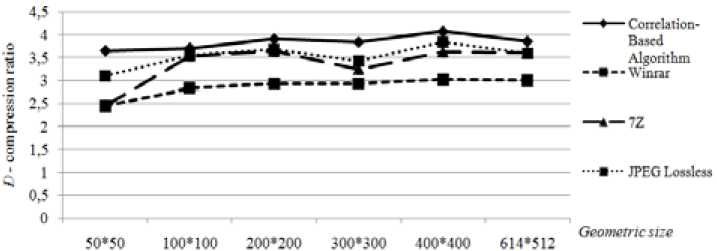
Fig. 2. Lossless compression algorithms at various size

The results of the experiment based on the compression algorithms degree taking into account the correlation and the number of groups show that the recommended parameter values are as follows: N = 2 – 10. This demonstrates that the subtraction (differential conversions) are effective with large range of channels in the group, then the average values of differences Sr are the least (Fig. 3), so this allows to store in the smallest amount on a disk space than the small amount of K in N .

In Fig. 4-5 depicts the dependencies on various parameters of the experiments performed showing the modification of the compression ratio, for example, at N = 5 (D>4), N = 9 (D>4,5).

According to the results of experiments based on the dependence of the correlation from the chosen channels groups and the best channel it is revealed that when the value Cor is reduced then K is reduced proportionally. To study the effectiveness of the proposed compression method with the use of choosing the groups of the most correlated channels, there have been done the experiments on the number of filling channels, which show that when K = [5:50] the compression degree is higher than when K = [50:100], Fig. 6.

Conclusion

On the basis of the conducted researches the following conclusions should be drawn: the compression lossless algorithm considering intrabands correlation allows to increase the compression degree to (D>4,5) than in the universal archivers and JPEG Lossless algorithm; the proposed approach of finding the best groups of channels for a given correlation value has increased the efficiency of the – 888 –

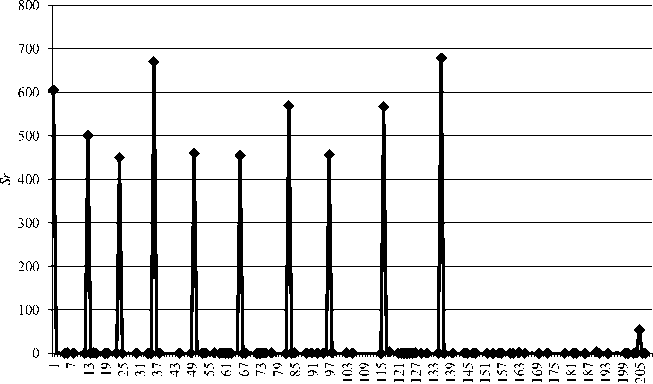
Fig. 3. Sr of the best channels and their differences

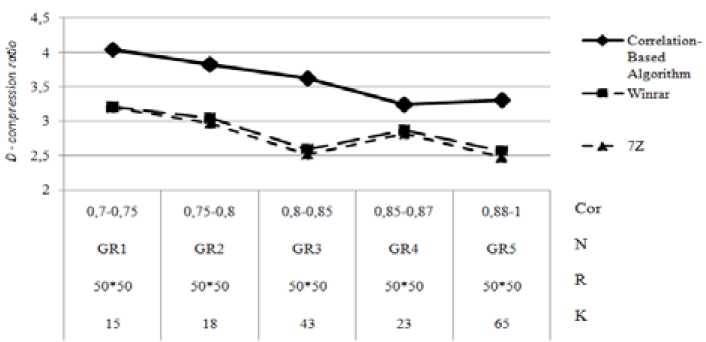
Fig. 4. Comparison of lossless compression algorithms for N = 5

use of channel subtraction phase (differential transformation); the obtained results of the comparison of the converted hyperspectral AI with archivers and JPEG 2000 Lossless allow to talk about the efficiency of the indexed encoding stages.

The perspectives for further researches can be encoding the transformed hyperspectral AI with an adaptive algorithm using regression analysis and a new model of interchannel correlation accounting.

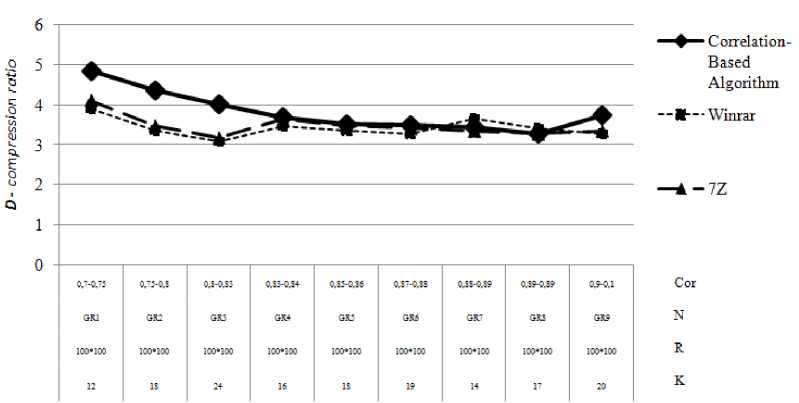
Fig. 5. Comparison of lossless compression algorithms for N = 9

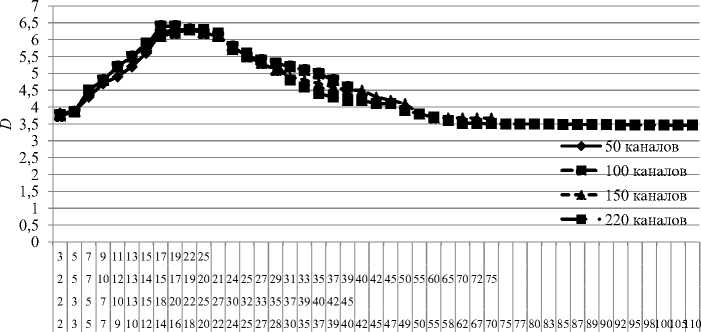
Fig. 6. The graph in number of filling the channels