The Impact of False Negative Cost on the Performance of Cost Sensitive Learning Based on Bayes Minimum Risk: A Case Study in Detecting Fraudulent Transactions
Автор: Doaa Hassan
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
In this paper, we present a new investigation to the literature, where we study the impact of false negative (FN) cost on the performance of cost sensitive learning. The proposed investigation approach has been performed on cost sensitive classifiers developed using Bayes minimum risk as an example of an applied mechanism for making a classifier cost sensitive. We consider a case study in credit card fraud detection, where FN refers to the number of fraudulent transactions that are miss-detected and approved as legitimate ones, assuming the classifier predicts the fraudulent transaction. Our investigation approach relies on testing the performance of various complex cost sensitive classifiers from different categories developed using Bayes minimum risk at different costs of FN. Our results show that those classifiers behave differently at different costs of FN including the real and average amount of transaction, and a range of random constant costs that are greater or less than the average amount. However, in general the results show that the lower the costs of FN are, the better the classifier performances are. This leads to different conclusions from the one drawn in [1], which states that choosing the cost of FN to be equal to the amount of transaction leads to better performance of cost sensitive learning using Bayes minimum risk. The results of this paper are based on the real life anonymous and imbalanced UCSD transactional data set.
Cost sensitive learning, fraudulent transactions, Bayes minimum risk
Короткий адрес: https://sciup.org/15010899
IDR: 15010899
Текст научной статьи The Impact of False Negative Cost on the Performance of Cost Sensitive Learning Based on Bayes Minimum Risk: A Case Study in Detecting Fraudulent Transactions
Published Online February 2017 in MECS
As the use of debit and credit cards has increased rapidly in the last years, the detection of fraud transactions committed with them and hence ensuring a secure electronic transaction has become a great challenge to achieve. Recently there has been many research work done to use data mining and machine learning to address this challenge as a classification problem [2], [3], [4], [5]. The main objective of this research work is to identify the fraudulent transactions from the genuine ones using knowledge discovery from infrequent patterns derived from the gathered data in order to make a valid prediction. The classification mechanisms used in this research were evaluated using the classical evaluation measures such as accuracy, precision and recall [6].
However, the specialty of credit card fraud detection is that misclassifying a fraudulent transaction as legitimate (false negative (FN)) carries a significant different cost more than the inverse case (false positive (FP)) and hence the costs of false positive and false negative errors should be unequal and can differ from an example to another. Therefore there is a clear certain need to take the misclassification cost into account when applying the various data mining classification techniques for identifying credit card fraud in order to avoid the costliest of errors.
Recently various research methods have been developed in the literature on credit card fraud detection to differentiate between the cost of wrongly predicting a fraudulent transaction as legitimate from the cost of the inverse case [1], [7], [8], [15]. Some of these methods assume different constant costs for each type of both predictions [7]. Other methods assume the real financial cost of credit card fraud detection [1, 15], while [8] assuming a lower constant cost for predicting legitimate transactions as fraudulent ones.
To this end and due to the fact that misclassifying fraudulent transactions as legitimates ones may cause a huge waste of money, this paper investigates the impact of the cost of FN on the performance of various complex cost sensitive classifiers used for credit card fraud detection. The cost sensitive classifiers developed using Bayes minimum risk have been considered for the presented investigation in this paper. This technique was proposed in [1] as a method for making the classifier cost sensitive. The aim of the presented investigation is to determine the best cost of FN that leads to the best performance of classifier. Therefore, we evaluate the performance of different types of cost sensitive classifiers developed using Bayes Minimum Risk at different costs of FN including either the real or average amount of transaction in addition to a range of constant values that are greater or less than the average amount. This evaluation methodology considers an inequality between the cost of FN and the cost of the FP (i.e., misclassifying legitimate transactions as fraudulent), where a lower administrative constant cost is assigned for FP. We have also considered a benefit cost for rightly detecting a fraudulent transaction. The “total cost” which is the summation of the misclassification and rightclassification costs of each test example of the entire test set of each classifier is used as a metric to evaluate the classifier performance. In this paper, the Bayes minimum risk classifier has been implemented and tested on different types of classifiers including support vector machine (SVM), decision trees (DT), random forest (RF), logistic regression (LR), neural network (NN) and Naïve Bayes [9]. As a result, various categories of cost sensitive classifiers have been obtained.
The structure of this paper is organized as follows: In Section II, we provide a background of cost sensitive learning and discuss the related work. In Section III, we introduce our investigation approach as well as the experimental settings. In Section IV, we present the performance evaluations. In Section V, we provide some discussions in view of the performance evaluation results. Finally we conclude the paper in Section VI with some directions for future work.
-
II. Backgroud
-
A. Cost Sensitive Learning Based on Bayes Minimum Risk
The accuracy of classifying a data set is commonly used in machine learning field as a metric to evaluate the performance of classifiers. However, some types of misclassifications may affect badly than others. For example, rejecting authorized access to a system may cause inconvenience while authorizing an illegitimate access may be more dangerous and cause very negative consequences. Here the role of cost sensitive learning appears, where the cost of every type of error is taken into account in order to avoid errors that lead to catastrophic situations [10].
In view of this, the goal of cost-sensitive learning is to use the cost matrix [10] to represent the cost of each type of misclassifications. In such a case, the cost matrix is considered as the dominant factor to find the border between the regions that divide optimally the example space. For example if misclassifying class i is more expensive relative to other classes then the region of class i must be expanded at the expense of other classes, even though there was no change in the class probabilities.
As for credit card fraud detection, let us consider the cost matrix shown in Table 1. The matrix is two dimensional matrix where the rows of the matrix represent the cost for the actual values of the class label (Xi) which has two possible values 1 for fraud or 0 for legitimate respectively. Similarly, the columns of the matrix represent the cost for the predicted values of the class label (xi) which has also two possible values: 1 for fraud or 0 for legitimate respectively. The matrix entry Cij is the cost of predicting the jth class label when the ith class label is actually correct. Thus, the cost matrix has the following four entries:
-
• C 11 refers to the cost of predicting the credit card
transaction as fraud and it is actually fraud.
-
• C 01 refers to the cost of predicting the credit card
transaction as fraud and it is legitimate.
-
• C 10 refers to the cost of predicting the credit card
transaction as legitimate and it is fraud.
-
• C 00 refers to the cost of predicting the credit card
transaction as legitimate and it is actually legitimate.
In general, the correct prediction when j = i is cheaper than the incorrect prediction when j≠ i . So in most cases, the entries C ii , and C jj which are equivalent to the True Positive (TP) and True Negative (TN) in the confusion matrix of the classifier [11], along the main diagonal will all be zero. Using the cost matrix, the optimal prediction of an example x is the class j that minimizes a loss function L (i.e., the cost measure) defined for each j as the sum over the other alternative possibilities of the true class of x as follows:
Цх,^ = '^Р^Сч
Table 1. A cost matrix for credit card fraud detection
|
Cost Matrix |
Predicted Class |
||
|
Actual Class |
C(1|0) |
Fraud |
Legitimate |
|
Fraud |
C 11 |
C 10 |
|
|
Legitimate |
C 01 |
C 00 |
|
This cost matrix will be used for evaluating the classifier that predicts the fraudulent transactions, where each transaction in the data set is classified as fraud or legitimate based on the value of the loss function calculated in (1). Thus, the transaction is classified as fraud if the expected cost of this prediction is less than or equal to the expected cost of predicting this transaction as legitimate, and it is classified as legitimate otherwise. Formally, this can be expressed according to the cost matrix shown in Table 1 as follows:
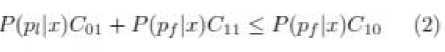
where (p f |x) and (p l |x) represent the probabilities of a transaction being fraud and legitimate respectively and there is no cost for true negative (TN) due to predicting the legitimate transaction as legitimate (i.e., C 00 =0).
Equation (2) implements the Bayes minimum risk algorithm [12]. In this paper we develop various cost sensitive classifiers from different categories using the Bayes minimum risk algorithm. This is achieved by classifying each transaction in the testing set of each classifier as fraudulent or legitimate according to the condition in (2).
-
B. Related Work
There have been some research attempts that investigated the cost sensitivity of classification to evaluate credit card fraud detection systems. For example, the work presented in [13] introduced a multi-classifier meta-learning approach to address the issues of skewed class distribution and nonuniform cost per error. The approach was applied to reduce the loss due to illegitimate transactions for the credit card fraud problem.
R.J. Bolton and D. J. Hand [14] reviewed the previous research that suggested a cost for Visa/MasterCard fraud and introduced a cost model to accompany the different classification outcomes in order to minimize the fraudulent loss.
-
Y. Shain et al. [8] presented a cost sensitive decision tree approach for fraud detection that minimizes the sum of misclassification costs while selecting the splitting attribute at each non leaf node.
J. Wang et al. [27] developed cost-sensitive algorithms for solving the problem of an online cost-sensitive classification task. Their algorithms were designed to directly optimize the two widely known cost-sensitive measures, namely the maximization of weighted sum of sensitivity and specificity , and the minimization of weighted misclassification cost .
The work presented in this paper is inspired by the work introduced in [1], where the Bayes’ risk classifier is used in combination with the cost matrix to build RF and LR cost sensitive classifiers. The cost matrix proposed in [1] assigns a real financial cost for wrongly classifying a fraudulent transaction as legitimate one (FN) and a lower constant cost for the inverse case (FP). Our approach extends this work by assigning a negative administrative cost (i.e., benefit) for rightly detecting fraudulent transactions. Moreover, we investigate the impact of FN cost on the performance of various common complex cost sensitive classifiers developed using Bayes minimum risk by testing their performance at different costs of FN and determine which cost of FN leads to the best performance of the classifier.
-
III. Basic Approach
We study the effect of the cost of FN that it has on the performance of cost sensitive classifiers developed using Bayes minimum risk in order to detect the fraudulent transactions. Since the concept of cost sensitive learning relies on assigning a cost for misclassifying fraudulent transaction as legitimate one and the inverse case, therefore the first step in our approach is to assign values for the four entries in the cost matrix shown Table 1 as follows:
-
• We assign an administrative cost for the true positive (TP) (i.e., correctly identifying the fraudulent transaction) as a result for analyzing the transaction and rightly contacting the card holder. Hence we assign a value of C A1 to C 11 .
-
• We assign the cost of false positive (FP) (i.e., classifying a legitimate transaction as a fraudulent one) administratively as a result for analyzing the transaction and wrongly contacting the card holder. Hence we assign a value of Ca2 to C 01 .
-
• We assign the cost of false negative (i.e., classifying a fraudulent transaction as a legitimate one) to be equal initially to the real amount of the transaction (i.e., the amount of money stolen by this transaction) following the approach in [1]. Hence we assign the real value of transaction to C 10 .
-
• We assume that there is no cost for true negative (TN) (i. e., correctly classifying legitimate
transactions and hence we assign a zero value to C 00 .
-
• We repeat the procedure in the previous steps, but with assigning the average amount of transactions to the cost of FN (C 10 in the cost matrix in Table 1), then change it to other different random values that are either greater or less than the average amount of transactions.
Table 2 shows the new generated cost matrix after assigning values to its four entries. As shown in the table, we refer to the cost of FN for a transaction i with a variable FN_Ci that takes different values including the real, average amount of transactions and a range of random constant costs that are greater or less than the average amount. Using this cost matrix, the cost measure is defined as follows:
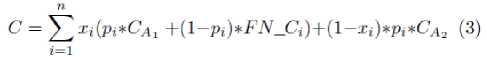
where n is the number of samples/transactions, C is the sum of costs of all elements in the cost matrix for n transactions (i.e., the total cost), x i is the actual class label of ith transaction and p i is the predicted class label for the same ith transaction. In the paper experiment Ca1 is set to -1 dollar (i.e., the bank customer will be charged one dollar by the bank when detecting a fraudulent transaction) as it is considered a benefit to identify a fraudulent transaction, while Ca2 is set to +1 dollar, due to incorrectly contacting the credit card holder.
Table 2. Setting values for the entries in the cost matrix.
|
Cost Matrix |
Predicted Class |
||
|
Actual Class |
C(F|L) |
Fraud |
Legitimate |
|
Fraud |
C A1 |
FN_C i |
|
|
Legitimate |
C A2 |
0 |
|
The second step in our approach is to develop cost sensitive classifiers from different categories based on Bayes minimum risk by re-expressing /re-implementing the condition specified by (2), according to the values of cost matrix entries shown in Table 2. Formally, this can be expressed as follows:
Р^НСл. +Р(Р/к)СЛ2 < P^pj^FN.Ci
Finally, the last step in our approach is to test the performance of each classifier in terms of the total cost for each value of FN_C i in order to figure out which cost of FN leads to the best classifier performance.
-
A. Experimental Environment
We have run our approach for investigating the influence of FN cost on the performance of cost sensitive learning based on Bayes minimum risk on a windows laptop machine with 2.6 GHZ processor Intel core (TM) i5 and 4 G Memory Rams. We have used Weka [15], a free open source software data mining tool to generate different classifiers from different categories and train them on the experimental data set. The choice of Weka is ideal for our experiment since it allows us to easily solve the imbalanced data set problem [16] using Weka filters [17] to create a balanced subsample of the data set as we will see in the next two subsections. Moreover, it allows us to obtain the probabilities of a transaction being fraud or legitimate that we need for developing cost sensitive classifiers based on Bayes minimum risk as expressed by (2). Next we implement the Bayes minimum risk algorithm in python and test it on the testing sets of all classifiers generated by Weka and calculating the total cost in each case.
-
B. UCSD transactional data set
The basic experiment of this paper has been performed on UCSD transactional data set [18]. This data set was used before for detecting odd e-commerce transactions as presented in [19], [20]. It has 94682 examples of real ecommerce transactions, where 92,588 of them are legitimate transactions and the remaining 2094 transactions are fraudulent with a fraud ratio of 2.2%. The data set has 19 attributes/ features, 8 of them are nominal while the remaining 11 features are numerical in addition to a class attribute. Since the data set is large and imbalanced (i.e., there is a class imbalance, where the number of fraudulent transaction is too small in comparison to the number of legitimate ones), our experiment is done with under-sampling [21] the data set by selecting smaller subset of transactions (subs-ample) of the data set for training and testing the generated classifiers. The sub-sample contains 4690 instances, where 2345 of them are legitimate transactions and the remaining are fraudulent with a fraud ratio of 50.0%. We have used all transactions in the sub-sample as training and test data, where we split the sub-sample into training (66.67%) and testing (33.33%). The training sub-sample has 3126 transactions where 1565 are legitimate and the remaining 1561 transactions are fraudulent with a fraud ratio of 49.94%. The testing sub-sample has 1564 instances, where 780 instances are legitimate and the remaining 784 transactions are fraudulent with a fraud ratio 50.13%. In order to make the test data set reflects the real fraud distribution of 2.2 as % in the original data set, we have resampled the test data set sub-sample again
and get a new testing sub-sample with 797 transactions, where 780 of them are legitimate and 17 are fraudulent with a fraud ratio of 2.13%. The weka.filters package [22] has been used to resample the data set.
-
C. Experimental Procedure
The experimental procedure of our approach has the following steps:
-
• Generating various classifiers from different categories including DT, SVM, NN, NB, LR, and RF. More precisely the J48, SMO, MultilayerPerceptron, Naivebayes, Logistic, and RandomForest implementations respectively in Weka. We train those classifiers on the experimental training sub-sample of UCSD data set. By generating and training the classifiers using Weka, we can get the probabilities of a transaction being either fraud or legitimate.
-
• Developing cost sensitive classifiers from different categories based on the Bayes minimum risk algorithm specified by (4) using the cost matrix shown in Table 2 and the obtained probabilities in the previous step for each trained classifier.
-
• Testing all the developed cost sensitive classifiers by predicting each instance (i.e., transaction) in the UCSD testing set sub-sample for each classifier as fraud or legitimate according to the condition given in (4).
-
• Calculating the total cost for each cost sensitive classifier created in the previous step based on the cost measure given in (3) and for each value of FN_C i in the cost matrix shown in Table 2. FN_C i takes the values of either the real or the average amount of transaction in addition to a range of values that are greater or less than the average amount of transaction.
-
• Evaluating the performance of each classifier in terms of the total cost, for each value of FN_C i .
-
IV. PERFORMANCE EVALUATION AND RESULTS
We have tested the impact of FN cost on the performance of cost sensitive learning using Bayes minimum risk for detecting credit card fraud by reporting about the performance of each classifier, for each value of FN in terms of the total cost as presented in (3). Table 3 shows the results of performance evaluation of each classifier when the cost of FN is equal to the real and average amount of transactions, or when it has a random constant cost greater than or less the average amount of transaction (e.g., 100, 50, 10, 7, 5, and 2 respectively). From the results shown in Table 3, we have noticed the following:
-
• When the cost of FN is equal to either the real or average amount of transaction, we found that SVM is the best as it achieves the most saving, while DT is the worst among all developed
complex cost sensitive classifies. Moreover, we found that SVM also achieves the best accuracy, while DT has the worst accuracy among all complex classifiers. Fig. 1. and 2. show the misclassification cost and accuracy for each classifier in each case.
-
• The performance of all classifiers is improved by achieving a lower cost (i.e., more saving) when the cost of FN resulting from predicting the fraudulent transaction as legitimate one decreases as shown in Fig. 3.
Table 3. The performance of cost sensitive classifiers in terms of total cost in dollar with different costs of FN.
|
Cost of FN |
DT |
SVM |
NN |
NB |
LR |
RF |
|
Real amount |
673 |
165.75 |
207 |
455 |
560 |
594 |
|
AVG=24.48 |
673 |
174.43 |
205 |
464 |
588 |
629 |
|
100 |
715 |
401 |
240 |
644 |
736 |
736 |
|
50 |
673 |
251 |
220 |
558 |
682 |
691 |
|
10 |
673 |
131 |
190 |
335 |
455 |
494 |
|
7 |
350 |
122 |
176 |
296 |
396 |
443 |
|
5 |
334 |
116 |
163 |
268 |
342 |
389 |
|
2 |
158 |
107 |
144 |
187 |
222 |
253 |
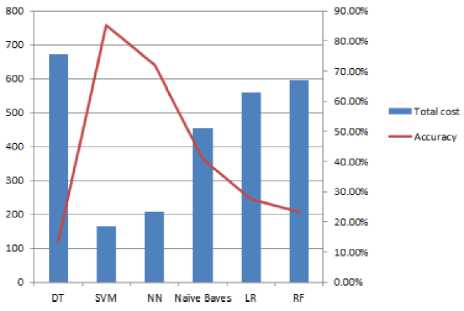
Fig.1. The total cost and accuracy of classifiers when the cost of FN is equal to the real amount of transaction.
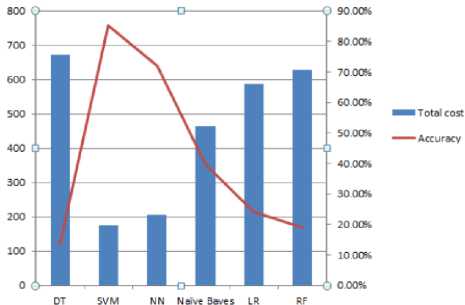
Fig.2. The total cost and accuracy of classifiers when the cost of FN is equal to the average amount of transaction.
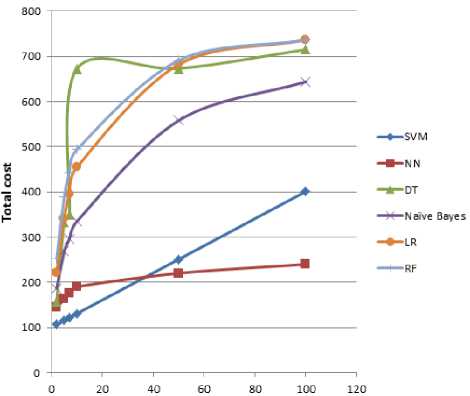
Fig.3. The performance of cost sensitive classifiers when the cost of FN =100 or 50 or 10 or 7 or 5 or 2.
-
V. Discussion
In the following, we discuss some remarks about the effect of FN cost on the performance of cost sensitive learning algorithms developed using Bayes minimum risk for identifying the credit card fraud. In view of the evaluation results that we have obtained in the previous section, we can conclude the following:
-
• The performance of the cost-sensitive learning using Bayes minimum risk is related to cost of FN, where the former is inversely proportional to the later.
-
• The learning algorithms that have been made cost sensitive based on Bayes minimum risk and which were presented in [1, 26] in order to identify credit card fraud, namely logistic regression (LR) and random forest (RF) are not the best in performance among all tested complex classifiers. SVM, NN and Naive Bayes outperform those classifiers by achieving more cost saving as shown in Fig. 1, 2. and 3.
-
• The performance of all classifiers when the cost of FN is equal to the real amount of transaction is much closed or similar to the performance of those classifiers when the cost of FN has a constant value that is equal to the average amount of transaction as Fig. 1 and 2 show respectively.
-
• Assigning the real amount of transaction to FN does not lead all the time to the best performance by achieving the lowest cost with all complex classifiers categories as illustrated in Table 3. This contradicts what is mentioned in [1] regarding the positive effect of assigning the real cost of transaction to the cost of FN on improving the performance cost sensitive classifiers developed based on Bayes minimum risk.
-
VI. Conclusions
In this paper, we have conducted a new study on the impact of assigning different costs for false negative (FN) in the cost matrix on the performance of various costsensitive classifiers. We have considered the Bayes minimum risk as a method for developing cost sensitive classifiers. Moreover, the credit card fraud detection has been considered as a case of study, where FN refers to misclassifying the fraudulent transaction as legitimate. We have evaluated the performance of those classifiers in terms of the total cost which is the summation of the misclassification and right classification costs of each test example in the entire test set. We have tried various costs for FN starting from the real amount of transactions up to small administrative constant cost values, where there is a small constant difference between the costs of FN and FP. Our results show that though assigning a high cost for FN should be considered for detecting credit card fraud, there is always a tradeoff between the cost of FN and the performance of the cost-sensitive classifier, where the lower the costs of FN are, the better the classifier performances are. Therefore, the choice of the best cost of FN that leads to the best performance of cost sensitive classifier remains a challenge.
As a future work, we are planning to apply our approach for investigating the influence of assigning different costs for FN on the performance of various cost sensitive classifiers developed using other techniques different from Bayes minimum risk such as Metacost [23], threshold optimization [24] and those presented in [25]. Also we are looking forward to applying our investigation approach to other case studies different from credit fraud detection such as unauthorized access detection.
Acknowledgment
I am so grateful to Predrag Radivojac at Indiana University- Bloomington for his significant contribution to this work and for various discussions and suggestions. Also I would like to thank the reviewers of this paper for their insightful comments.
Список литературы The Impact of False Negative Cost on the Performance of Cost Sensitive Learning Based on Bayes Minimum Risk: A Case Study in Detecting Fraudulent Transactions
- Alejandro Correa Bahnsen, Aleksandar Stojanovic, Djamila Aouada, and Bj¨orn E. Ottersten. Cost sensitive credit card fraud detection using bayes minimum risk. In 12th International Conference on Machine Learning and Applications, ICMLA 2013, Miami, FL, USA, December 4-7, 2013, Volume 1, pages 333–338, 2013.
- Clifton Phua, Vincent C. S. Lee, Kate Smith-Miles, and Ross W. Gayler. A comprehensive survey of data mining-based fraud detection research. CoRR, abs/1009.6119, 2010.
- John Akhilomen. Data mining application for cyber credit-card fraud detection system. In Advances in Data Mining. Applications and Theoretical Aspects - 13th Industrial Conference, ICDM 2013, New York, NY, USA, July 16-21, 2013. Proceedings, pages 218–228, 2013.
- Sitaram patel and Sunita Gond. Supervised machine (svm) learning for credit card fraud detection. International Journal of Engineering Trends and Technology (IJETT), 8(3), 2014.
- Masoumeh Zareapoor and Pourya Shamsolmoali. Application of credit card fraud detection: Based on bagging ensemble classifier. Procedia Computer Science, 48:679–685, 2015.
- Precision and recall. Available at: https://en.wikipedia.org/wiki/Precision_and_ recall.
- D. Hand, C. Whitrow, N. M. Adams, P. Juszczak, and D. Weston. Performance Criteria for Plastic Card Fraud Detection Tools. Journal of the Operational Research Society, 59(7):956–962, 2007.
- Yusuf Sahin, Serol Bulkan, and Ekrem Duman. A Cost-Sensitive Decision Tree Approach for Fraud Detection. Expert Syst. Appl., 40(15):5916–5923, 2013.
- P.-N. Tan, M. Steinbach, and V. Kumar. Introduction to Data Mining. Addison-Wesley, 2005.
- Charles Elkan. The foundations of cost-sensitive learning. In Proceedings of the Seventeenth International Joint Conference on Artificial Intelligence, IJCAI 2001, Seattle, Washington, USA, August 4-10, 2001, pages 973–978, 2001.
- Confusion matrix. Available at: https://en.wikipedia.org/wiki/Confusion_ matrix.
- Predrag Radivojac. Machine learning lecture notes. February, 2015.
- Philip K. Chan and Salvatore J. Stolfo. Toward scalable learning with non-uniform class and cost distributions: A case study in credit card fraud detection. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining (KDD-98), pages 164–168, 1998.
- Richard J. Bolton, David J. Hand, and David J. H. Statistical fraud detection: A review. Statistical Science, 17(3):235–249, 2002.
- Weka 3: Data mining software in java. Available at: http://www.cs.waikato.ac.nz/ml/weka/.
- Xinjian Guo, Yilong Yin, Cailing Dong, Gongping Yang, and Guangtong Zhou. On the class imbalance problem. In 2008 Fourth International Conference on Natural Computation, volume 4, pages 192–201. IEEE, 2008.
- Remco R. Bouckaert, E. Frank, M. Hall, R. Kirkby, P. Reutemann, A. Seewald, and D. Scuse. Weka manual (3.7.1), 2010.
- Ucsd-fico data mining contest 2009 data set. https://www.cs.purdue.edu/ commugrate/data/credit card/.
- K. R. Seeja and Masoumeh Zareapoor. Fraudminer: A novel credit card fraud detection model based on frequent itemset mining. The Scientific World Journal, 2014:10 pages, 2014.
- Minyong Lee, Seunghee Ham, and Qiyi Jiang. E-commerce transaction anomaly classification, 2013.
- J. V. Hulse and T. M. Khoshgoftaar. Experimental perspectives on learning from imbalanced data. In International Conference on Machine Learning, 2007, pages 155–164, 2007.
- http://weka.wikispaces.com/Primer. September, 2010.
- Pedro M. Domingos. Metacost: A general method for making classifiers cost-sensitive. In Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, August 15-18, 1999, pages 155–164, 1999.
- Victor S. Sheng and Charles X. Ling. Thresholding for making classifierscost-sensitive. In Proceedings, The Twenty-First National Conference onArtificial Intelligence and the Eighteenth Innovative Applications of ArtificialIntelligence Conference, July 16-20, 2006, Boston, Massachusetts, USA, pages 476–481, 2006.
- Michael J. Pazzani, Christopher J. Merz, Patrick M. Murphy, Kamal M. Ali, Timothy Hume, and Clifford Brunk. Reducing misclassification costs. In Proceedings of the Eleventh International Conference on Machine Learning, Rutgers University, New Brunswick, NJ, USA, July 10-13,1994, pages 217–225, 1994.
- Alejandro Correa Bahnsen, Example dependent cost sensitive classification: Applications in Financial Risk Modeling and marketing analytics. PhD thesis, University of Luxembourg, 2015.
- J. Wang, P. Zhao, and S. C. H. Hoi. Cost-Sensitive Online Classification. IEEE Transactions on Knowledge and Data Engineering, 26(10):2425–2438, Oct. 2014.
- Lopamudra Dey, Sanjay Chakraborty, Anuraag Biswas, Beepa Bose, Sweta Tiwari,"Sentiment Analysis of Review Datasets Using Naïve Bayes' and K-NN Classifier", International Journal of Information Engineering and Electronic Business(IJIEEB), Vol.8, No.4, pp.54-62, 2016. DOI: 10.5815/ijieeb.2016.04.07.


