The Lyapunov stability of the Cauchy-Dirichlet problem for the generalized Hoff equation

Let Q C R ^s Ite a bounded domain with boundary d Q of class C^x . Consider the generalized Hoff equation [1] in cylinder Q x R

( A — А о) Ut + A Ut = a i u + a 2 U + ... + anu , n G N .             (1)

This equation models the bending of an I-beam. Here the function u = u ( x,t ) , ( x, t ) G Q x R Is the displacement of the beam, from the vertical position. The parameter A G R+ corresponds to a, constant vertlcal load and the parameters ai G R. i = 1 , 2 , ...,n characterize the material of the beam.

Consider the initial-boundary value problem

u ( x, 0) = u ₀( x ) , x G Q; u ( x,t )=0 , ( x, t ) G d Q x R               (2)

for equation (1). This problem was firstly considered in [2-4], wherein it was found out that the problem is essentialy unsolvable for arbitrary initial data. The set of initial values, which guarantees the existence and uniqueness of solution to initial-boundary value problem for equation (1), has been studied in [5]. If n = 2 and a 1 ■ a2 G R+ then the phase space of equation (1) is a simple Banach C ^ -manifold. This result was obtained in [6]. And if a 1 ■ a2 G R - then the phase space of equation (1) lies on the Whitney fold. It is shown in [7]. The generalized Hoff equation (for n >  3) was considered in [8], but in this paper the stability has not been studied. This result was obtained in [9] for the case when n = 3. Generalized Sobolev type equations have been studied in other papers, for example, in [10]. In this paper we generalize the results of [9] and consider the case when n >  3.

The paper consists of two parts. The first part is devoted to the reduction of problem (1), (2) to the Cauchy problem u (0) = u о

for abstract semilinear Sobolev type equation

Lui = Mu + N ( u ) .

Here L, M are linear operators and N is nonlinear operator defined on specially constructed functional spaces. The second part is devoted to the study of stability of stationary solution to problem (1), (2). This is the main result.

• 1.    Phase Space

◦

Consider spaces U = W1 (Q). F = W- 1(Q) and operators

Lu v) = /(( A - A °) uv -V.^« ) dx, Su, v _eW1 (^Q) ,

Ω

Muv = a 11 uvdx, Vu.v ^e L 2 n (^Q) ,

Ω

(N ( u ) , v) = y( a 2 u ³ + ... + an- 1 u ² n- ³ + anu ² n- 1) vdx Vu,v e L2n (Q) .

Ω

◦

Embedding W 21 (Q) ^ L2n (Q) is dense and continuous. Therefore L,M e L (U; F). and L is a Fredholm operator. The spectrum of the operator L is real and discrete, has finite multiplicity and condenses only to —to. Operator N e C^x (U; F).

A vector function u e C^ю (U , F) satisfying equation (4) is called a solution of this equation.

Definition 1. A set P C U is called a phase space of equation (3) if the following conditions are satisfied:

• (i)    each solution u = u ( t ) of (4) lies in P pointwisely: i.e.. u ( t ) e P for all t e R;

• (ii)    for each u ° e P, there exists a unique solution to problem (3), (4).

Theorem 1. Let n = 1 , 2 when s = 4 (i.e. Q C R4J, n = 1 , 2 , 3 when s = 3 (i.e. Q C R³ J and n e N wh en s = 1 , 2 (i.e. Q C Ro r Q C R²). Then one of the two conditions is satisfied

• (i)    if ker L = { 0 }. then the. phase space, of (''.quation (1) concidcs with U.

• (ii)    if ker L = { 0 }, and all coefficients ai e R \{ 0 }, i = 1 , ...,n have the same sign. Then the phase space of eqiation (1) is simple manifold

  M =

  

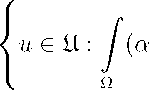
  1 + a 2 u ²

  
  

  + ... + anu ^{2 n} 2) uxkdx = 0 , k = 1 ,.

  
  
  
  
  

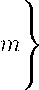
• 2.    Stability

Here xk ^are orthonormal eigenfunctions (corresponding to the eigenvalues Ak оf L.

P.O. Moskvicheva, I.N. Semenova

Definition 2. A family of mappings S is called a nonlinear semigroup in a normed space V if for every u G V and some т = т ( u ) 6 R+ the following conditions are satisfied:

• (1)    S = S ( t, u) G V. for all t G ( —т ; т) ; S (0 , u) = u:

• (11)    S ( t + s, u ) = S ( t, S ( s, u )) for all t + s G ( —т, т ).

A point u G V such that S ( t, u ) = u,t G R is called a stationary point.

Definition 3. A stationary point u is called

• (i)    stable (in sense of A.M. Lyapunov), if for any neighborhood O_u оf u there exists a neighborhood O'_u (i.e. not necessarily the same neighborhood) of the same point, such that S ( t, v ) G O'_u for all v G O_u arid t G R₊:

• (ii)    asymptotically stable (in sense of A.M. Lyapunov), if it is stable and for any point v in some neighborhood O_u оf u S ( t, v ) ^ u for t ^ to.

Definition 4. A functional V G C (V; R) is called a Lyapunov functional if

• • _{z x} --------1 _z .......

^{V ( u} ) = ?^{т ( V ( S ( t,u} )) - ^{V ( u} )) ^{- 0}

t^ 0+ t for all u G V.

Theorem 2. Let u be a stationary point. If there exists a Lyapunov functional such that

• (i)    V ( u ) = 0:

• (ii)    V ( v ) > ф (|| v — u^ ); here ф is strictly increasing continuous function such that ф (0) = 0 aiid ф ( r ) >  0 f(ir r G R₊. then tlгс point u is stable.

Theorem 3. Let the conditions of Theorem 2 be satisfied, and a strictly increasing continuous function ф. such that ф (0) = 0 anul ф ( r )   >  0 for r G R₊. exist. If

V ( v ) — —ф ( ||v — u| ). then tltc point u is asymptotically stable.

We will study the stability of problem (1),(2) using Theorems 2 and 3.

◦

Consider a space U (= W 2) with norm || ■ | | of space L<2. It is an incomplete normed space. Define the Lyapunov functional by formula

V ⁽ u ) = У⁽ u x +⁽ ^ о

Ω

— A ) u 2) dx.

Obviously V (0) = 0 arid V ( u ) > c|u|2. Moreover multiph'lug (1) scalarly in L2 bу u we obtain

! /( u ) = —a i |u| ² — a 2 |u| L 4 — ... — a_n|u| L 2 _n.

Since the embedding L2_n ^ L2 is obvious, the following inequality holds

V ^ ^{( u} ) ^{— —a} 1 ll uh ^{2 — a} 2 ^c 2 ll uhL 4 ^— . . . ^{— a}n^cn^|u| Ln _n .

Here Cj,j = 1 , n are the constants of embedding. Function constructed from the norm || ■ | | on the right side of (8) satisfies the conditions of Theorem 3. So we have proved the following theorem.

Theorem 4. Zero solution of problem (1), (2) is asymptotically stable for any aj E R₊ , j = 1n,X E [0 ,A 0].