The neural correlates of exact calculation in word and numerical formats in low and high math performers: a fNIRS study

People use two cognitive systems to understand and operate numbers - non-symbolic system, primarily relying on magnitude estimation without symbols (e.g., Arabic numerals), and symbolic system, based on processing of numbers in symbolic form ( Ansari, 2008 ; Feigenson, Dehaene and Spelke, 2004 ; Waring and Penner-Wilger, 2017 ). Development of numerical cognition is a gradual process that started from the nonsymbolic or approximate number system. Approximate number system is an innate cognitive system that supports the estimation of the magnitude without relying on language or symbols. However, the role of symbolic representations of quantity and basic arithmetic skills increases with age ( Artemenko, 2021 ). Basic arithmetic skills are of great importance in everyday life, in STEM education, and in many sciences that involve math: in physics, chemistry, technology and engineering, in various IT applications. Better understanding the underlying brain mechanisms of simple and complex exact calculations is important for numerical cognition and gives an insight into the relation between different brain areas within a network associated within the approximate number system and exact symbolic representation system. In practice, this knowledge can be used in the future in order to improve a person’s numerical skills, eliminate problems associated with their lack (decrease in arithmetic and mathematical literacy, dyscalculia). It has been shown that all these shortcomings can have negative consequences for both the economy and society as a whole ( Butterworth, Varma and Laurillard, 2011 ). Therefore, the practical

© 2023 by the authors. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license .

significance of the results is substantiated by public demand.

Previous studies at the behavioral level aim to investigate the development of numerical abilities based on both approximate non-symbolic and exact symbolic representations from infancy to adult-hood. Experimental evidence shows that infants as young as six months old can differentiate between two arrays of dots as consisting of a different number of objects ( Xu and Spelke, 2000 ). By the age of eighteen months, toddlers can distinguish the order of numbers and choose the larger array of dots, indicating their understanding of relative quantity ( Brannon, 2002 ). At the age of three, children can accurately estimate the number, a concept known as cardinality. In elementary school, children learn about numbers as a representation of numerical values in a non-symbolic format, which is followed by the development of an exact symbolic representation system ( Ansari and Karmiloff-Smith, 2002 ). The symbolic system allows for the processing of discrete numbers and is considered the foundation for math skills such as counting, estimation, addition, subtraction, and other precise numerical calculations ( Ansari, 2008 ; Mundy and Gilmore, 2009 ; Waring and Penner-Wilger, 2017 ). Calculations are studied immediately after digits at the same stage of numerical cognition, indicating the importance of the symbolic system ( Von Aster and Shalev, 2007 ; Vanbinst et al., 2016 ; Schneider et al., 2017 ).

Reviews on neurophysiological mechanisms associated with exact calculations, indicate the predominant role of the fronto-parietal network in numerical processing, the role of which changes with age ( Moeller et al., 2015 ; Nieder et al., 2016 ; Clark et al., 2017 ; Peters and Smedt, 2018 ; Vogel and Smedt, 2021 ). Intraparietal sulcus and precuneus in the parietal region, the frontal cortex (e.g., superior and medial frontal gyri), the claustrum, the insula and cingulate are the main structures involved in numerical cognition ( Arsalidou and Taylor, 2011 ). Additionally, inferior temporal and fusiform gyri are associated with processing the numerical shapes and symbols, necessary for calculations with Arabic digits ( Piazza and Eger, 2016 ). Exact calculations are associated with dorsolateral prefrontal cortex, ventrolateral prefrontal cortex, posterior superior parietal lobe, intraparietal sulcus, supramarginal gyrus, angular gyrus, fusiform gyrus, and hippocampus ( Vogel and Smedt, 2021 ). Activation in the frontal cortex overlaps with areas implicated in language processing (Broca’s area), working memory and cognitive control ( Stuss and Knight, 2013 ; Devlin, Matthews and Rushworth, 2003 ; Fadiga and Craighero, 2006 ; Gentilucci et al, 2006 ; Barbey, Koenigs and Grafman, 2013 ).

The role of brain structures depends on the specificity of operations such as addition, subtraction, multiplication and division, as well as task characteristics such as format (numerical and word problems) ( Obersteiner et al., 2010 ; Dresler et al., 2009 ), complexity of arithmetic problems (simple or complex nocarry or no-borrow or carry and borrow, respectively) ( Artemenko et al. 2018a ), age ( Peters and Smedt, 2018 ; Vogel and De Smedt, 2021 ), and level of math performance ( Meiri et al., 2012 ; Artemenko et al. 2018b ). Studies have shown that arithmetic operations such as addition and subtraction are determined by the necessity of carry/borrow effects and processing of magnitude, with carry and borrow operations increasing the difficulty of such problems ( Klein et al., 2010 ). The carry means a digit that is transferred from units to tens if the sum of units is more than ten when addition is performed. The borrow means a digit that is transferred from tens to units, if minuend is less than subtrahend when subtraction is performed. The activation of both frontal and parietal regions, including the left inferior frontal gyrus, bilateral middle frontal gyrus, superior frontal gyrus, and left intraparietal sulcus, accompanies carry and borrow effects ( Artemenko et al. 2018b ). The two-digit calculations require greater working memory load for processing magnitude information and visual identification, with Broca’s area, inferior frontal gyrus and left fusiform gyrus being among the neural correlates of complex addition and subtraction, associated with phonological processing, verbal working memory, and visual identification of digits ( Dahaene and Cohen, 1995 ; Pollack and Ashby, 2018 ).

Recent studies have discussed the role of interconnected areas associated with arithmetic calculations, including the prefrontal, posterior parietal, occipito-temporal, and hippocampal areas, in children compared to adults. ( Peters and Smedt, 2018 ). Mental calculation based on the manipulation of numerical symbols develops with age, and structures associated with symbolic numerical processing may also become more prominent as children grow older. The dynamics is supposed to be influenced by an increase in mathematical competencies; thereby, math skills can influence neural changes in the brain networks involved in the math performance. Thus, Soltanlou et. all (2018) state that the development of psychophysiological mechanisms for the calculations occurs in accordance with the fron-to-parietal shift, known as a shift in brain activation during calculations from frontal structures, in particular precentral premotor and motor areas in children, to parietal regions in adults, reflecting a shift from a labor-intensive procedural to more automatic strategies between ages 8 and 19 ( Rivera et al., 2005 ; Kaufmann et al., 2006 ; Kucian et al., 2008 ; Artemenko et al., 2018b ).

Individuals may develop mathematical competencies differently, and their level of performance in math may reflect different neural representations of numerical skills. Some researchers have found differences in activation dependent on math ability in the intraparietal sulcus (Park et al. 2012; Prado et al. 2011). As reported by Artemenko et. all (2018a), some researchers found activation differences in the left angular gyrus (Grabner et al. 2007, 2011; Menon et al., 2000). These differences in activation may be associated with increased or decreased angular gyrus activation depending on processing efficiency or experience/training (Amalric and Dehaene 2016; Grabner et al. 2007, 2011). Additionally, low math performers have shown higher activation in the dorsolateral prefrontal cortex during error processing (Ansari et al., 2011). The intraparietal sulcus, right dorsolateral prefrontal cortex, and left angular gyrus may be influenced by math ability during single-digit arithmetic in multiple ways (Artemenko et al. 2018a), but the underlying process remains unknown. Furthermore, adults with high mathematical abilities demonstrate higher activation in frontal regions during calculations accompanied by carry and borrow effects, which contradicts the fronto-parietal shift (Artemenko et al. 2018a).

Overall, exact calculation, whether it involves complex or simple math problems, rely on parietal brain areas (intraparietal gyrus, angular gyrus, supramarginal gyrus), which represent domain-specific processes, occipital (inferior temporal gyrus and fusiform gyrus) and frontal areas (interior frontal gyrus and middle frontal gyrus), which represent domain-general processes. There are various mechanisms involved in arithmetic processing and mental calculation, which can be attributed to either domain-general processes that are related to cognitive processing in general or domain-specific processes that are specifically linked to mathematical performance ( Gilmore et al., 2018 ). Number magnitude processing, which is associated with domain-specific processes, is located in the intraparietal sulcus (IPS) ( Artemenko, 2021 ). Among domain-general processes that play an important role in calculation are working memory, which is represented in left inferior frontal gyrus (IFG) and bilateral middle frontal gyrus (MFG, and fact retrieval, which is represented in supramarginal gyrus (SMG) and angular gyrus (AG).

According to the most influential model of numerical cognition (Triple-Code Model) there are three representative codes for number: analogue non-symbolic representations of quantity (in particular, the ability to estimate the number of objects without counting), verbal-phonological representations of quantity (words denoting Arabic numbers, and oral counting), and visual representations of Arabic numbers ( Dahaene and Cohen, 1995 ; Dehaene et al., 1999 ). Each of these representations is provided by functionally separate brain mechanisms ( Lavander-Ferreira, 2020 ). Numerical representations of number activate the lower parietal regions of both hemispheres, while tasks with numerical codes (Arabic numbers) activate the fusiform gyrus of both hemispheres. Finally, the semantic designations of the number, represented by verbal information, cause activity in the left perisylvian areas and the left angular gyrus. However, most studies investigate only one specific representations, rather than all three at the same time. Moreover, the Triple-Code Model does not explain how the brain performs calculations for math word problems. Monti, Parsons and Osherson (2012) demonstrated the role of different areas of the brain in syntactic tasks and algebraic operations. Fuchs et al. (2006) showed the importance of arithmetic word problems as a cognitive predictor of arithmetic calculations in the Assessment of Math Fact Fluency test of the Math Battery, which incorporates two subtests: Addition Fact Fluency and Subtraction Fact Fluency. Differences in brain activation patterns are found in the calculation or simple reading of two-digit addition problems involving a numerical or text format ( Richter et al., 2009 ). In another study ( Dresler et al., 2009 ), higher average oxygenation is demonstrated in the parietal and posterior frontal regions for calculation compared to reading in word problems in primary and secondary school students. Comprehension skills influence arithmetic word problem performance. Thus, it is shown that even for successful word problem solvers, performance decreases if the text of the word problem is semantically complex ( Boonen et al., 2016 ). Daroczy et al. (2015) consider some components of word problem difficulty, such as the linguistic complexity of the problem text itself, the numerical complexity of the arithmetic problem, and the relation between the linguistic and numerical complexity of a problem. Moreover, two factors complicate the solution of word problems: linguistic and numerical complexity ( Verschaffel, Greer and De Corte, 2000 ). However, most researchers do not consider these factors together in their study.

The problem of exact calculations has been examined in various studies. However, tasks that require different formats, such as reading or basic calculation have not been thoroughly investigated. Studying the neural mechanisms of different formats of exact calculation tasks might help to provide evidence for or against the Triple-code model. Recent studies provide arguments against Triple-code model. For example, Skagenholt et al. (2018) examined all three modes of representative codes for number simultaneously to identify the neural correlates of number processing in adults (N=46) using fMRI. The analysis of the task-control condition contrast revealed task-dependent activity, which can be seen as partial support for the Triple-Code model, but also revealed a complex distributed fron-to-parietal network involved in all numerical codes. The results show that the Triple-Code Model correctly predicts the existence of some functionally dissociated neural substrates, but needs to be up-dated to consider the interactions with attentional processes. Contrasts corresponding to differences in task complexity revealed specific neural correlates of the numerical distance effect (i.e., numbers that are close together are more difficult to distinguish than numbers that are farther apart). The connectivity analysis demonstrated overlapping of neural correlates in all tasks, confirming the notion of a fron-to-parietal number processing network. Thus, the authors offer arguments in favor of revising the Triple-Code Model.

The comparison of the brain mechanisms involved in numerical or word format calculations is promising for educational neuroscience ( Dresler et al., 2009 ). Arithmetic math problems with numerals embedded in text that describe everyday situations are common in school curricula. However, math problems with numbers written in words (for example, “forty-seven plus twenty-one is…”) are not typical in education. Problems of this type are thought to be related to alternative mechanisms of numeral manipulation. Research in this area may be useful in finding effective ways of teaching mathematics, especially for children with math difficulties who have problems processing numerical symbols. It is important to understand the neural correlates of math problem calculations in various formats, paying special attention to individual differences, particularly, math performance.

The aim of the present study is to measure brain activation in frontal and parietal regions reflected in oxygenation changes measured by fNIRS and to estimate the differences in neurocognitive foundations of exact calculation problems (addition) in numerical or word formats in non-overlearned conditions (twodigit numbers) in young adults who vary in level of math competencies. This study addresses the brain mechanisms of exact calculation problems represented both in traditional format for educational system (problems with numerals in Arabic notation) as well as atypical format (problems with numerals written in words). Thus, we consider the influence of linguistic complexity on solving word problems. In addition, we focus on processing math problems in various formats by students with different levels of mathematical ability. The results obtained will contribute to a better understanding of the nature of domain-specific or domain-general processes in the brain that accompany exact calculations, and can be applied in educational neuroscience, for example, for develop new types of math problems.

The hypotheses of the present study are:

H1 - Tasks in word and numerical formats of exact calculation can cause activation in different areas of the brain, since these two formats of presenting arithmetical problems differ in the amount of cognitive effort needed and in the brain processes involved in calculation.

H2 - Brain activation during solving exact calculation in a word format might involve “language” areas, such as Broca’s area, and occipital (ITG, and fusiform gyrus) and frontal areas (IFG and MFG) that represent domain-general processes.

H3 – Individual differences based on levels of math competencies are expected to be observed.

Materials and Methods

Participants and Procedure

Sixty-five adults were recruited through a university mailing list to participate in the study. All subjects were native Russian speakers, have normal or corrected-to-normal vision and do not have any history of neurological or mental disorders. Some participants were excluded from the sample due to noisy NIRS data (n=7), technical difficulties (n=2), and very poor behavioral results (n=3). For the present analysis, the remaining subjects were divided into groups according to their performance in solving addition and subtraction problems in word and numerical formats. We calculated error rates of 53 participants in 100 addition and subtraction problems with and without carry procedure in a word format and 100 addition and subtraction problems with and without borrow procedure in a numerical format. Participants, who correctly solved more than 70 % of math problems in a word format and more than 85% of math problems in a numerical format formed the group with high level of math competencies (n=19). Those who solved less than 50 % of math problems in a word format and less than 65% of math problems in a numerical format formed the group with low level of math competencies (n=17). Participants from both groups significantly differed in solving math problems (see Table 1). The final sample consists of 36 subjects aged 18-25 (M = 19,5, SD = 1,877, 41 females). Participants provided an informed consent to participate in the study and received a monetary reward for their time and effort. The study was approved by the Ethics Commission of Psychological Institute of Russian Academy of Education, 2020/11-3.

Materials

The experiment consisted of 225 arithmetic problems presented on the computer screen. There were addition and subtraction exact calculation problems and some math problems for reading only. In the present study only addition tasks that included 50 problems in a numerical format with Arabic numerals (for example, 45+23=), and 50 problems in a word format with numerals written in Russian (for example, fifty-six plus seventy-one is) of different complexity levels: with and without carry procedure were analyzed. 25 tasks were presented as a math problem without calculation embedded in text (for example, Ann had 15 flowers and Teddy brought her 32 flowers more. How many flowers did Teddy bring to Ann?).

Addition and subtraction tasks were represented by two-digit numbers in both operands with a two-digit solution not exceeded 100 in each task. The main selection criteria for two-digit addition and subtraction tasks were to induce computational efforts, but not guessing or retrieving results from declarative memory ( Kong et al., 2005 ) since when using the recall strategy, arithmetic skills are not involved and, and other parts of the brain were activated ( Ischebeck et al., 2006 ; Zago et al., 2001 ). Pure decades (e.g., 20), as well as tie numbers (e.g., 44) were not used in exact calculation tasks, since they were much easier to solve (for a similar procedure see ( Dresler et al., 2009 ; Klein et al., 2009 ; Artemenko et al., 2018b ). In two-digit mathematical problems in a word format, a simple logico-mathematical scheme to compute the quantities in the problem based on the assumption that the word problem is only numerical was applied.

Procedure

The recent study is a part of a larger experiment. The duration of this part of the experiment was 30 minutes. The measurement was conducted individually with each participant seated comfortably in front of the computer screen. Each session began with an introduction to the NIRS measurement and the experimental procedure.

During fNIRS measurement, participants were instructed to perform exact calculation tasks in two different modalities (types): in a numerical format (condition 1), and in a word format (condition 2), as well as to read without calculating the arithmetic problems embedded in text (condition 3). The experiment was in a block design, with a total number of 25 blocks, with an inter-block-interval of 20 s for a short rest. There were three conditions in the experiment: (1) addition exact calculation problems in a numerical format (10 blocks); (2) addition exact calculation problems in a word format (10 blocks); (3) reading condition (5 blocks). Each measurement started with an fNIRS resting state recording for 3 minutes. The number of trials was limited and equal for all participants. The sequence of the blocks within each condition and conditions themselves was randomized. Before each condition there were detailed instructions presented on the screen, and 3 training trials. No feedback was given to participants.

The trial started with a fixation cross, presented for 0.5 – 0.8 s in a randomized order to prevent adaptation to it, and was followed by the arithmetic task for 4.5 s. After that, an empty screen with a grey block to insert the answer appeared for 2.5 s. The sequence of a trial is shown in Fig. 1. If no answers were presented within the given time, the next trial appeared on the screen. The participant had an opportunity to correct the answer if a mistake was made within the limited time of 2.5 s. In our study we applied a written production paradigm as the most typical format of giving the solution for the math problem in the education system. In a written production paradigm, adults had to type in the solution to the math problem with the help of numerical keyboard as quickly and accurately as possible.

Figure 1. Scheme of a trial

Participants were instructed to read the problems silently and choose one out of two numbers in a reading condition, or calculate mentally in exact calculation conditions. The participants could either wait until the time for presenting the stimulus finished or press the spacebar as soon as they had calculated the problem or completely read it and chosen the answer, respectively.

The exact calculation and reading only problems were presented horizontally in white against a dark grey background at the center of the computer screen using the free software package PsychoPy ( Peirce, 2007 ).

fNIRS data acquisition fNIRS recordings were acquired using the mobile near-infrared spectroscopy device NIRSport Model 88 (NIRx Medical Technologies, LLC, NY, the USA) with eight light- emitters and eight photodetectors. A probeset of 14 channels, with an interoptode distance of 30 mm, was integrated into an elastic cap to cover the frontal and parietal brain regions of both hemispheres (see Fig.2). All optodes were positioned according to the 10-20 system (Jasper 1958), with the center in P3 and P4 positions in the parietal region, and in F1 and F2 in the frontal regions. Two near-infrared laser beams with wave-lengths of 760 and 850 nm were emitted, and the sampling rate was 7.8125 Hz. The correspondence of fNIRS channels to the underlying cortical areas was estimated using the fNIRS optode’s location decider (fOLD), software (Zimeo Morais, Balardin and Sato, 2018), which utilizes the Automated Anatomical Labeling 2 (AAL2) atlas (Tzourio-Mazoyer et al. 2002; Rolls, Joliot and Tzourio-Mazoyer, 2015) for probing arrangement.

In our study, we defined 4 regions of interest (ROIs) that included parietal and frontal regions known from previous studies to be related to exact calculation and reading arithmetic problems. In the parietal brain area, ROIs were formed in the left hemisphere by channels S1-D1 (left angular gyrus, intraparietal sulcus, Wernicke), S1-D2, and S2-D1 (left supramarginal gyrus), S2-D2 (left middle temporal gyrus), S2-D3 (left inferior temporal gyrus, fusiform gyrus); and in the right hemisphere by channels S3-D4 and S3-D5 (right angular gyrus, intraparietal sulcus), S4-D4 (right supramarginal gyrus), and S4-D5 (right middle temporal gyrus). In the frontal brain, area ROIs were formed in the left hemisphere by channels S5-D6 (Broca’s area, left inferior frontal gyrus), S5-D7 and S6-D7 (left middle frontal gyrus); and in the right hemisphere by channels S7-D8 and S8-D8 (right middle frontal gyrus) (channels can be found at Fig.2).

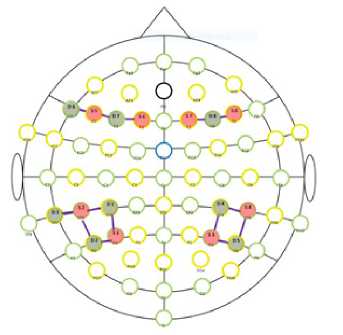
Figure 2. Probeset used for the fNIRS measurements indicating optode positions (red - source, green - detector) and channels that are formed by source-detector pair (violet lines)

Behavioral analysis

The results of the participants were analyzed for task performance (accuracy score) and reaction time (response time, RT). The accuracy score was calculated as the number of correct answers divided by the total number of trials. Response time (RT) was defined as the time from when grey box for inserting the answer appeared until the time when the actual answer was given or the space bar was pressed (see Table 1).

The estimation of accuracy score and response time differences by group and task type was performed by a two-factor repeated measures ANOVA with partial eta-squared as the effect size measure. Post-hoc comparisons were conducted using pairwise repeated measures t-test with Tukey correction. The analysis was performed in R 4.1.2 and Jamovi 2.2.3.

Statistical analysis of NIRS data fNIRS data was preprocessed and analyzed using a custom script based on free software packages MNE-fNIRS (Esch et al, 2019; Luke et al., 2020). MNE provides complete data analysis pipelines and toolboxes in Python for fNIRS data processing.

During fNIRs data preprocessing, the raw intensity values were first converted to optical density. At this stage, the coupling quality between the scalp and optodes was quantified using the scalp coupling index (SCI index, for detailed description see Pollonini et al., 2014). The SCI index helps to detect a strong cardiac oscillation in fNIRS raw signals, which is undesirable for measuring evoked cortical hemodynamic responses (Themelis et al., 2004). By applying this method to raw data of all participants, we scanned all channels to find out the presence of synchronous signals in the frequency range of cardiac signals across both photodetected signals. Channels with SCI below 0.6 were marked as bad channels and eliminated from any further analysis. Remaining noisy channels in filtered data were interpolated using the mean of the surrounding channels (nearest method). To remove motion artifacts from the analyzed data, the temporal derivative distribution repair filter (TDDR) was applied (Fishburn et al., 2019). According to recent studies, the TDDR filter shows better results when applied to the optical density of fNIRS data before calculating the relative concentration changes of hemoglobin (Fishburn et al., 2019). Next, the relative concentration changes of oxygenated (O2Hb) and deoxygenated hemoglobin (HHb) were estimated for every channel using the modified Beer-Lambert law. However, in this study, we focused on the parameter O2Hb as several researchers regarded this hemoglobin chromophore more sensitive to changes in cerebral blood flow (Hoshi, Kobayashi and Tamura, 2001; Dresler et al., 2009). Finally, we applied a 0.02-0.2 Hz bandpass filter to the data to remove heart rate oscillations as well as slow drifts.

To separate and remove physiological confounds from fNIRS data, a general multivariate regression model (general linear model, GLM) analysis ( Yücel et al., 2021 ; Luke et al., 2021 ) available in the MNE-NIRS package ( Yucel et al., 2021 ) was applied to examine the task-specific neural activity associated with reading, exact calculation in a numerical format, exact calculation in a word format in two experimental groups. We modeled the expected neural response for each experimental condition using the SPM hemodynamic response function (HRF) combined with the stimulus event times and durations. All fNIRS signal changes unrelated to task-specific neural responses were marked as drifts, and included in the design matrix as cosine drift regressors. We specified 5 regressors with a 1/ high pass filter cut off (in our case 0.002 Hz). For every group three contrasts, such as (1) reading versus addition exact calculation in a numerical format; (2) reading versus addition exact calculation in a word format; (3) addition exact calculation in a numerical format versus addition exact calculation in a word format) based on beta-values were calculated.

Additionally, to test if there were task-specific neural activation compared to a non-task baseline activation we compared all three task-related contrasts with resting-state derived contrast. Resting-state was used in our study as a baseline marker of brain activity. Resting state may be considered as a brain activity without work load or any purposeful cognitive process activated and assumed as a ‘baseline’ for any comparison with task specific activity ( Hurlburt et al., 2015 ), however this view sometimes argues ( Morcom and Fletcher, 2007 ). In our study 3 minutes resting state with closed eyes was used as a new condition with activity unrelated to math or reading. Comparison of three experimental conditions with resting state allowed tracing of changes specific related to calculation and reading in general. Resting state with close eyes was analyzed.

Bootstrapping (random sampling with replacement) with 200 iterations for multiple comparisons correction for every contrast in both groups was applied to reduce the risk of the type I error (false positive) and to overcome the possible problems caused by small samples. Bootstrapping estimates properties of estimands by sampling from an approximating distribution. In our study we applied the following scheme for bootstrapping: first were randomly chosen 14 subjects from the main sample (random sampling), on the next step three contrasts were calculated 200 times (a numerical format versus a word format of the calculation; a word format of calculation versus reading; a numerical format of the calculation versus reading) and 200 beta values for each channel was obtained. A median value for each channel out of 200 iterations was set as a typical beta value for this channel. The significance of each channel was defined based on Z criterion, so that if in more than 50% of iterations the significance was true, the channel was marked as significant. For analyses of statistically significant differences between groups, the pairwise comparisons were made using permutation Mann-Whitney test.

Results

Behavioral results

Table 1 presents the results of the participants’ task performance accuracy and response time (RT) are presented in Table 1. The lowest accuracy and response time were observed for calculation problems in a word format. While performing the reading task, both experimental groups showed consistent performance, however, the accuracy was lower and response time was higher across all conditions for low-performers.

Table 1

Mean scores and mean response time within three experimental conditions in groups of high-level and low-level performers

Group	Task	Accuracy		Response Time
		Mean	SD	Mean	SD
high	reading	0.930	0.0445	2.70	3.38
	num	0.865	0.109	3.16	2.85
	word	0.652	0.175	5.05	3.36
low	reading	0.851	0.239	3.05	3.04
	num	0.678	0.143	3.94	2.77
	word	0.341	0.152	5.72	2.23

Note. num – a numerical format of the exact calculation, word – a word format of exact calculation, high – group with high level of math competencies, low - group with low level of math competencies

Table 2 presents the results of the ANOVA comparison between task format and group. The analysis showed significant (p < 0.01) differences in the accuracy across the three task conditions (reading, calculation problems in a word format, calculation problems in a numerical format), as well as significant interaction between task format and group. Regarding response time, only the tasks showed significant differences, with no difference observed between high and low groups.

Table 2

Within and between subjects’ effects in task and group comparison

	Sum of Squares		Mean			P	П2р
			df	Square	F
				Accuracy
	Task	2.691	2	1.3456	117.86	<.001	0.792
Within Subjects Effects	Task * group	0.223	2	0.1115	9.77	<.001	0.24
	Residual	0.708	62	0.0114
Between	group	0.916	1	0.9155	18.8	<001	0.377
Subjects Effects	Residual	1.511	31	0.0487
Response Time
	Task	111.656	2	55.828	15.234	<.001	0.330
Within Subjects Effects	Task * group	0.831	2	0.415	0.113	0.893	0.004
	Residual	227.207	62	3.665
Between	group	8.81	1	8.81	0.46	0.503	0.015
Subjects Effects	Residual	594.62	31	19.18

Table 3 presents the results of the post-hoc analysis conducted on the ANOVA results. The analysis indicated significant differences in the accuracy among all groups (defined by task format and group). Regarding response time, significant differences were observed only between the calculation task in a word format and the other two task formats. The calculation task in a word format showed significantly higher response time than the other two tasks.

Table 3

Post-hoc comparison

Accuracy
	Factor	Factor	Mean Difference	SE	df               t		Ptukey
		calculation, a
Task		numerical	0.12	0.0267	31	4.49	<.001
	reading	format
		calculation, a word format	0.394	0.032	31	12.33	<.001
	calculation, a	calculation, a
	numerical	word format	0.274	0.0185	31	14.81	<.001
	format
Group	high	low	0.192	0.0444	31	4.33	< 001
Response Time
	Factor	Factor	Mean Difference	SE	df	t	Ptukey
		calculation, a
Task		numerical	-0.674	0.411	31.0	-1.64	0.245
	reading	format
		calculation, a word format	-2.514	0.522	31.0	-4.81	<.001
	calculation, a	calculation, a
	numerical	word format	-1.840	0.474	31.0	-3.88	0.001
	format
Group	high	low	-0.597	0.881	31.0	-0.678	0.503

Note. high – group with high level of math competencies, low - group with low level of math competencies

fNIRS results

We used GLM analysis and estimated the activation of brain areas for each of three experimental conditions based on statistically significant channel-specific effects, assessed by thresholding a test statistic Z ( Yucel et al., 2021 ). Individuals with high level of math competencies showed significant neural activation in the left angular gyrus (AG), intraparietal sulcus (IPS), and in left inferior frontal gyrus (IFG), and deactivation in the left middle temporal gyrus, specifically in a numerical format of the exact calculation task (Fig. 3, a). In contrast, in the same condition, the group with low level of math competencies showed no significant activation (Fig. 3, b).

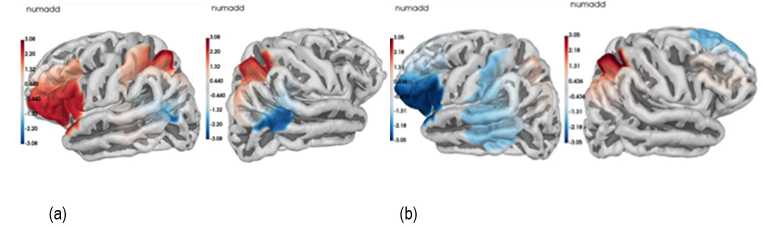
Figure 3. Activation associated with a numerical format of calculation task in (a) group with high level of math competencies, and (b) group with low level of math competencies

Note. Numadd – addition task in a numerical format

Regarding a word format of the exact calculation task, individuals with high level of math competencies did not demonstrate any significant neural activation. However, individuals with low level of math competencies showed significant activation in the right middle frontal gyrus (MFG), right angular gyrus (AG), and intraparietal sulcus (IPS) (Fig. 4, b).

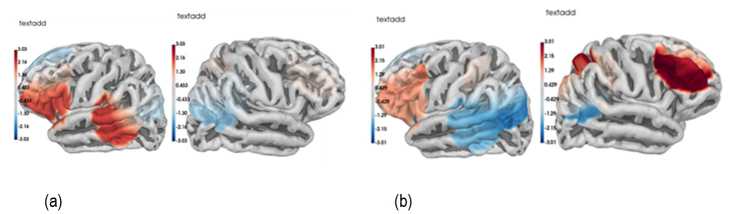
Figure 4. Activation associated with a word format of calculation task in (a) group with high level of math competencies, and (b) group with low level of math competencies

Note. Textadd – addition task in a word format

Regarding the reading condition (without calculation), subjects with high level of math competencies showed increased activation in the left middle temporal gyrus and fusiform gyrus (Fig. 5. a). In contrast, in the same experimental condition, subjects with low level of math competencies showed no significant activation.

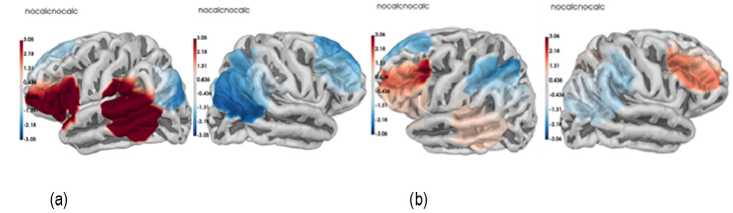
Figure 5. Activation associated with reading of math problem without calculation in (a) group with high level of math competencies, and (b) group with low level of math competencies

Note. Nocalc – reading

On the second level of GLM analysis, the coefficients of neural activation in each channel within different experimental conditions were compared between individuals in a group with high level of math competencies, as well as between individuals in a group with low level of math competences. In the group of individuals with high level of math competencies, significant activation was identified in the reading task, in comparison to a numerical format and a word format of the exact calculation tasks, in the inferior temporal gyrus and fusiform gyrus (Tables 4 and 5).

Table 4

Beta coefficients of second level of GLM contrast “reading task versus a numerical format of calculation” in high level performers

	Coef.	Std.Err.	z	P>|z|	Significant
ch_name[S1_D1]:Chroma[hbo]	-2.684609	2.499011	-1.074305	0.282686	False
ch_name[S1_D2]:Chroma[hbo]	-2.102969	2.499011	-0.841520	0.400056	False
ch_name[S2_D1]:Chroma[hbo]	-1.237461	2.499011	-0.495181	0.620473	False
ch name[S2 D2]:Chroma[hbo]	2.977359	2.499011	1.191415	0.233401	False
ch_name[S2_D3]:Chroma[hbo]	6.620436	2.499011	2.649223	0.008068	True
ch_name[S3_D4]:Chroma[hbo]	-3.919274	2.499011	-1.568330	0.116804	False
ch_name[S3_D5]:Chroma[hbo]	-3.444847	2.499011	■1.378484	0.168054	False
ch_name[S4_D4]:Chroma[hbo]	-0.600722	2.499011	-0.240384	0.810033	False
ch_name[S4_D5]:Chroma[hbo]	-0.072426	2.499011	-0.028982	0.976879	False
ch_name[S5_D6]:Chroma[hbo]	1.130424	2.499011	0.452348	0.651018	False
ch_name[S5_D7]:Chroma[hbo]	-1.517347	2.499011	-0.607179	0.543732	False
ch_name[S6_D7]:Chroma[hbo]	-0.980016	2.499011	-0.392162	0 694939	False
ch name[S7D8]:Chroma[hbo]	-1.659906	2.499011	-0.664261	0.506523	False
ch_name[S8_D8]:Chroma[hbo]	-1.588489	2.499011	-0.635647	0.525006	False

Table 5

Beta coefficients of second level of GLM contrast “reading task versus a word format of calculation” in high level performers

	Coef.	Std.Err.	z	P>|z|	Significant
ch_name[S1_D1]:Chroma[hbo]	-0.434118	1.767808	0.245569	0.806016	False
ch_name[S1_D2]:Chroma[hbo]	-1.122363	1.767808	0.634890	0.525500	False
ch_name[S2_D1]:Chroma[hbo]	-0.131702	1.767808	0.074500	0.940612	False
ch_name[S2_D2]:Chroma[hbo]	0.609404	1.767808	-0.344723	0.730302	False
ch_name[S2_D3]:Chroma[hbo]	4.884222	1.767808	-2.762869	0.005730	True
ch_name[S3_D4]:Chroma[hbo]	-2.391980	1.767808	1.353077	0.176031	False
ch_name[S3_D5]:Chroma[hbo]	-1.276862	1.767808	0.722286	0.470119	False
ch_name[S4_D4]:Chroma[hbo]	-0.008876	1.767808	0.005021	0.995994	False
ch_name[S4_D5]:Chroma[hbo]	-1.172701	1.767808	0.663364	0.507097	False
ch_name[S5_D6]:Chroma[hbo]	1.470108	1.767808	-0.831599	0.405635	False
ch_name[S5_D7]:Chroma[hbo]	-0.989686	1.767808	0.559838	0.575590	False
ch_name[S6_D7]:Chroma[hbo]	-0.066429	1.767808	0.037577	0.970025	False
ch_name[S7_D8]:Chroma[hbo]	-2.006148	1.767808	1.134822	0.256450	False
ch_name[S8_D8]:Chroma[hbo]	-1.958984	1.767808	1.108143	0.267800	False

In the group of individuals with low level of math competencies, a different pattern of significant neural activation was found. In the reading task, in comparison both to a numerical as well as to a word formats of the exact calculation task, significant activation was identified in the inferior frontal gyrus (IFG) and middle frontal gyrus (MFG), particularly in the Broca’s area (Tables 6 and 7).

Table 6

Beta coefficients of second level of GLM contrast “reading task versus a numerical format of calculation” in low level performers

	Coef.	Std.Err.	z	P>|z|	Significant
ch_name[S1 _D1]:Chroma[hbo]	-3.321510	1.777946	-1.868173	0.061738	False
ch_name[S1_D2]:Chroma[hbo]	-0.570957	1.777946	-0.321133	0.748110	False
ch_name[S2_D1]:Chroma[hbo]	-0.013137	1.777946	-0.007389	0.994105	False
ch_name[S2_D2]:Chroma[hbo]	1.863506	1.777946	1.048123	0.294582	False
ch_name[S2_D3]:Chroma[hbo]	2.526878	1.777946	1.421234	0.155249	False
ch_n a me [S3 D4]: C h rom a [h bo]	-2.227532	1.777946	-1.252868	0.210254	False
ch_name[S3_D5]:Chroma[hbo]	-0.983827	1.777946	-0.553350	0.580023	False
ch_n a me [S4 D4]: C h rom a [h bo]	-1.586537	1.777946	-0.892343	0.372209	False
ch_name[S4_D5]:Chroma[hbo]	-1.355199	1.777946	-0.762228	0.445924	False
ch_name[S5_D6]:Chroma[hbo]	3.982777	1.777946	2.240100	0.025084	True
ch_name[S5_D7]:Chroma[hbo]	3.862199	1.777946	2.172281	0.029834	True
ch_name[S6_D7]:Chroma[hbo]	-1.183841	1.777946	-0.665848	0.505508	False
ch_name[S7_D8]:Chroma[hbo]	1.821818	1.777946	1.024676	0.305516	False
ch_name[S8_D8]:Chroma[hbo]	1.176466	1.777946	0.661699	0.508164	False

Table 7

Beta coefficients of second level of GLM contrast “word versus a numerical format of calculation” in low level performers

	Coef.	Std.Err.	z	P>|z|	Significant
ch_name[S1_D1]:Chroma[hbo]	-0.859091	1.822687	-0.471332	0.637403	False
ch name[S1 D2]:Chroma[hbo]	-2.613143	1.822687	-1.433676	0.151665	False
ch_name[S2_D1]:Chroma[hbo]	2.323436	1.822687	1.274731	0.202404	False
ch name[S2 D2]:Chroma[hbo]	-1.516720	1.822687	-0.832134	0.405333	False
ch name[S2 D3]:Chroma[hbo]	-0.071017	1.822687	-0.038963	0.968920	False
ch_name[S3_D4]:Chroma[hbo]	-0.408854	1.822687	-0.224314	0.822513	False
ch name[S3 D5]:Chroma[hbo]	0.865124	1.822687	0.474642	0.635042	False
ch name[S4 D4]:Chroma[hbo]	0.477964	1.822687	0.262231	0.793144	False
ch name[S4 D5]:Chroma[hbo]	-2.247213	1.822687	-1.232913	0.217608	False
ch name[S5 D6]:Chroma[hbo]	4.439445	1.822687	2.435660	0.014865	True
ch name[S5 D7]:Chroma[hbo]	2.818197	1.822687	1.546178	0.122062	False
ch name[S6 D7]:Chroma[hbo]	-0.281116	1.822687	-0.154232	0.877427	False
ch name[S7 D8]:Chroma[hbo]	2.050653	1.822687	1.125071	0.260559	False
ch name[S8 D8]:Chroma[hbo]	2.544455	1.822687	1.395991	0.162717	False

We also performed bootstrapping with 200 iterations for multiple comparisons correction for every contrast in both groups. Consistent results were found in a group of high-level performers, with significant neural activation in the inferior temporal gyrus and fusiform gyrus in the reading task in comparison to the calculation in a numerical format, but not in a word format. In the group of low-level performers, significant activation after bootstrapping remained in the left IFG, particularly in the Broca’s area, in a word format of the exact calculation task in comparison to a numerical format.

Furthermore, comparison of task-specific brain activation with brain activation during a 3 minutes resting-state revealed significant differences in low performers during the calculation task in a word format, with activation in the left IFG, particularly in the Broca’s area, and in the right MFG, as well as deactivation in the angular gyrus, Wernicke’s area, and IPS. In high-performers, significant differences were found in the reading task in the left IFG, particularly in the Broca’s area in a word format of the exact calculation task in the Broca’s area, as well as in the ITG and fusiform gyrus and in a numerical format of the exact calculation task in the right AG and IPS, as well as in Broca’s area.

As the experimental groups did not follow a normal distribution, we used the Mann-Whitney test to statistically compare neural activation between individuals with high and low levels of math competencies in reading task and exact calculation tasks, both in numerical and word formats. To correct for multiple comparisons, we used a post hoc permutation test with 90 iterations ( Ye et al., 2009 ; Yucel et al., 2021 ). Our analysis found statistically significant differences in neural activation in the exact calculation tasks in a numerical format in the right SMG and IPS (U=98, Z=6.9703, p=0.0455). We also observed marginal differences in the left SMG (U=100, Z=6.7507, p=0.0545).

Discussion

We analyzed and compared fNIRS data of subjects from two groups: with low and high levels of math competencies to detect the neural foundations of calculation of two-digits addition problems, both with and without carry effect, in two formats: numerical and word. Additionally, we added a third experimental condition of reading math problems without calculation to account for word processing, and linguistic complexity of text itself, and the relation between linguistic and numerical complexity within a math problem. Two out of three tasks/conditions in our experiment (a numerical format of calculation and reading arithmetic tasks embedded in text) were highly corresponding to school curriculum. However, the third one (a word format of calculation) is not typical for school mathematics tasks and could cause additional involvement of domain-general cognitive processes to solve them. This research is in line with studies investigating the effects of mathematical competency and math task format (numerical and word problems) ( Dresler et al., 2009 ; Obersteiner et al., 2010 ), as well as with studies that consider brain activation and individual differences in arithmetic performance ( Menon et al. 2000 ; Grabner et al. 2007 ; Artemenko et al., 2018a ). Our study revealed that young adults with high level of math competencies did not have significant differences in engaging frontal or parietal brain areas for solving exact calculation problems in numerical or word formats, while individuals with low level of math competencies recruited left frontal areas associated with language comprehension and understanding of complex sentences for processing problems in a word format, the same as for processing the reading task.

Mental calculation and reading in high level performers

In this study, GLM analysis revealed significant left hemisphere activation in the frontal and parietal regions for exact calculation tasks in exact calculation task in a numerical format, and in the left inferior temporal gyrus and left fusiform gyrus in reading tasks in individuals with a high level of math competencies. The activation of the left angular gyrus, left inferior temporal, and left fusiform gyri could be associated with domain-general abilities, while left IPS activation could be associated with both domaingeneral and domain-specific abilities. Angular gyrus, especially in the left hemisphere, has been shown to be associated with numerical and mathematical processing, particularly arithmetic problemsolving (i.e., mental arithmetic) ( Delazer et al. 2003 ; Zamarian, Ischebeck and Delazer, 2009 ; Seghier 2013 ). It could be linked to the retrieval of numerical information from memory ( Dehaene et al., 2003 ), but in our studyit could not be explained solely by fact retrieval. According to the recent review ( Sokolowski, Matejko and Ansari, 2022 ) recent research has suggested that AG activation in high performers could be due to the involvement in mapping numerical symbols and their meaning (symbol-referent theory), as well as engaging bottom-up attention required when an arithmetic solution was recalled from memory. Traditionally, IPS is considered a core region in processing symbolic numerical information and in calculation ( Matejko and Ansari, 2017 ). Left hemispheric IPS activation could be associated with symbolic arithmetic in Arabic notation ( Venkatraman et al., 2005 ; Artemenko et al., 2020 ). In terms of frontal regions, we found significant activation in the left inferior frontal gyrus, which is a language-related region of arithmetic processing involved in calculations and visuospatial processing ( Zamarin, Ischebeck and Delazer, 2009 ). Left angular gyrus, together with left inferior frontal gyrus, is thought to be involved in exact calculation ( Dehaene et al., 1999 ), and higher activation in the left angular gyrus is associated with a high level of arithmetic skills ( Grabner et al., 2007 ). Deactivation in the left middle frontal gyrus could be associated with decreased demand for working memory load due to automatization of addition. The left temporal gyrus, including the fusiform gyrus, is known to be involved in processing semantic information and word recognition.

The group level of GLM, as well as the bootstrap analysis, revealed brain patterns specific to the reading versus a numerical format of the calculation in the occipito-temporal region, particularly in the left inferior temporal gyrus and left fusiform gyrus. These regions are involved in recognizing symbolic objects ( Pammer, Korrel and Bell, 2014 ; Rüsseler et al., 2018 ) and processing the phonology of written characters while reading and comprehending text. The fusiform gyrus is also important for reading and can be impaired in dyslexia. Our results suggest that high performers experienced increased workload in reading skills, particularly in transcribing between number words, rather than in calculation skills. The absence of specific activation for math problems in a numerical format as well as in a word format may indicate that this group was able to perform calculations relatively easily without additional brain effort due to the involvement of domain-general processes.

Mental calculation and reading in low level performers

The results of the first level of GLM analysis in the group with low math competencies showed significant activation in the right hemisphere, specifically in the middle frontal gyrus (MFG), angular gyrus (AG), and intraparietal sulcus (IPS), but only in a word format of exact calculation task. The activation of MFG and AG is related to domain-general processes, while IPS is activated during both domain-general and domain-specific processes. In case of a word format of calculation task, angular gyrus might be associated with reading, and interpretation of what is written, as well as arithmetic processing. Within this group, a more workload was necessary for calculation in a word format. Thus, analysis revealed that some patterns of activation are not specific for this format. This finding can be used as an argument in favor of domain-general theories as opposed to domain-specific theories, particularly the Triple-code model. Overall, the calculation-induced increased activation in the parietal regions is consistent with the results of previous studies. In research by Richter et al. (2009) , participants calculated or read twodigit addition problems either in a numerical or text format. Calculations in both formats compared to reading task induced parietal activation. This may be partly related to the peculiarities of the tasks used in the study. The study also found that the carry effect was shown to activate several brain regions, including the intraparietal sulcus and the middle frontal gyrus. Previous studies demonstrated that the carry effect induced activation in the bilateral MFG, the cingulate cortex, the left IFG and the left IPS in tasks combining two-digit with single-digit operands ( Kong et al., 2005 ; Klein et al., 2009 ; Yi-Rong et al., 2011 ). Nevertheless, the carry effect and related brain activation analysis was not the aim of this study, so this problem requires further detailed analysis. In line with aforementioned studies, problems with carry effect used in our study in half of the trials might be a possible explanation for middle frontal gyrus that was activated during a word format of math problems. MFG involvement can be explained in two ways. One of them is a categorical effect that is based on the distinction of whether the carry operation has to be applied or not ( Klein et al., 2010 ; Verner et al., 2013 ). In our study participants were also constantly required to switch between tasks with carry operation and without it. Another explanation can be related to the working memory which supports the role of place-value integration arising during carry operation with multi-digit numbers ( Owen et al., 2005 ). The role of working memory in the carry effect in addition is highlighted by a number of authors ( Fürst and Hitch 2000 ; Imbo, Vandierendonck and De Rammelaere, 2007 ; Klein et al. 2010 ; Moeller, Klein and Nuerk, 2011a ; Moeller, Klein and Nuerk, 2011b ; Nuerk et al., 2011 ; Caviola et al., 2012 ; Göbel et al., 2014 ). Of particular importance is working memory capacity that can predict math performance ( Peng and Fuchs, 2016 ; Cragg et el., 2017 ; Fanari,Meloni and Massidda, 2019 ). According to a number of authors, the phonological loop (the verbal component of working memory) is crucial for exact calculations ( Frisovan den Bos еt al., 2013 ). The role of working memory in exact calculations is related to the phonological loop (the verbal component of working memory) being crucial for encoding and processing number words, which is important for math word problems solving. Additionally, working memory is involved in manipulating number words, such as performing arithmetic calculations and retrieving arithmetic facts from long-term memory ( Lavander-Ferreira, 2020 ). At the same time, our results support findings of other authors that confirm involvement of parietal areas in the carry effect ( Artemenko et al., 2018a ). Nevertheless, carry effect and related brain activation analysis was not the aim of this study, so this problem requires further detailed analysis.

Generally, the second level of GLM analysis and analysis after bootstrapping showed consistent results in the low performers. GLM revealed an increased activation in tasks involving word problems (a word format of exact calculation and reading task) in the frontal cortex, including Broca’s area, and IFG. Although Broca’s area and inferior frontal gyrus are thought to be crucial regions for speech production, some investigations demonstrated its involvement in comprehension of complex sentences ( Grewe et al., 2005 ). Our results are consistent with previous findings that report higher activation of inferior frontal regions in high-ambiguity sentence processing ( Rodd et al., 2005 ): possible ambiguity is associated with an unusual format for presenting math problems in a word format and arithmetic tasks embedded in text that do not require solving. Analysis after bootstrapping demonstrated an increased activation in exact calculations in a word format compared to numeric format in the Broca’s area and left inferior frontal gyrus. Thus, the predominant role of the frontal regions in comprehension was confirmed.

Differences between young adults from groups with high and low levels of math competences

It’s worth noting that significant activation in low performers was mostly in the same brain regions as in high performers, however in right hemisphere, but not in left hemisphere. In the literature there were some viewpoints that cerebral hemispheres played different roles in processing information depending on the solution strategy applied to solve the task. Solution-irrelevant interpretations of words in the problems might lead to rough semantic coding associated with the right hemisphere ( Beeman and Bowden, 2000 ).

Therefore, a possible explanation is that the right hemisphere is activated in stressful situations. In our case, for most individuals, due to their low math performance, solving exact calculation tasks in a word format was stressful. In support of this finding, previous studies found that right dorso-lateral prefrontal cortex (DLPFC) activation is associated with high trait anxiety ( Basten, Stelzel and Fiebach, 2012 ). MFG can be referred to as DLPFC. Klados et al., (2015) reported frontal changes during arithmetic calculation that are thought to be related to the influence of math anxiety on working memory. However, our results demonstrated activation patterns versus deactivation shown in some other studies ( Klados et al., 2015 ). Nevertheless, our assumption about the effect of anxiety needs additional investigation.

Another important finding was the detected specificity in the groups of low and high performers, which indicated differences in the mechanisms for solving the same type of tasks depending on the level of mathematical competence. This result is consistent with the neural efficiency hypothesis, according to which individuals with higher intelligence spend less brain resources on solving cognitive tasks ( Nussbaumer et al., 2015 ). This is expressed in the absence of differences in activation during solving math problems in various formats in high-level performers in our study. In low-level performers, there were significant differences in activation in different formats of exact addition problems solving. Between-groups comparison showed statistically significant differences in neural activation in exact calculation tasks in a numerical format as well in bilateral supramarginal gyrus (SMG) and right intraparietal sulcus. The SMG is known to be involved in complex calculation due to the high demands of visuospatial working memory ( Zago et al., 2001 ). Two-digit non-overlearned calculation is regarded as recruiting storage of intermediate results in a short-term memory to successfully solve the math problem ( Menon et al., 2000 ). Therefore, our findings might indicate specific activation for calculation based on the differences in performance.

Differences between task-induced activation and resting state

Comparison of brain activation during tasks and resting state also revealed a certain heterogeneity in brain mechanisms of math abilities. In the high performing group, all three conditions were associated with higher involvement of Broca’s area and inferior frontal gyrus, as well as some task-specific activation. As mentioned previously, the Broca’s area and IFG could be related to understanding complex sentences. Involvement of Broca’s area and IFG in the math processes could possibly be attributed to the reading of the actual presented stimulus ( Rogalsky, Matchin and Hickok, 2008 ; Klein et al., 2015 ). Reading numerals written in a word format in our study and subsequent analysis of semantics, however, might be related to two opposite processes. On the one hand, activation of speech-related areas could indicate the process of transformation of any numerical information into semantic form followed by the calculation process. On the other hand, it might reflect the process of transformation of any symbolic information into nonsymbolic form for the following calculations. Considering higher activation of Broca’s area in a word format of calculation in this study, we might have weak evidence for the second process, however this evidence is far from decisive and the first process might be more important for math abilities, both processes might operate simultaneously. This problem needs to be addressed additionally in future research. In the low-performing group, only a word format of calculation task significantly differed from resting state, with higher activation in Broca’s area, inferior frontal gyrus and middle frontal gyrus and lower activation in angular gyrus, Wernicke, and IPS. This pattern of activation seems to be consistent with the inter-task comparison. We detected no significant difference in activation between resting state, reading task and a numerical format of the calculation task. The absence of any task-induced activity could be the result of weak implication of executive functions ( Bull and Lee, 2014 ). People with weak executive functions demonstrate difficulties in remembering and following instructions, inhibiting irrelevant information and staying focused on task, as well as quickly choosing appropriate task strategies. There might be a substantial variability in brain mechanisms related to poor performance in calculations and this variability prevents statistically significant difference in activation induced by resting state and tasks. Therefore, high and low levels of performance in calculations might be attributed to different neurocognitive mechanisms.

Limitations

Our study has several limitations. Firstly, we have a relatively small sample size and have used group comparison as the primary method of assessing the level of math competence. Secondly, we did not fully estimate the differences between the two groups, and it may be important to use more appropriate methods for comparing group (or individual) performance within one condition. Thirdly, our analysis was limited to four areas of interest and did not cover the whole brain activity. Finally, we did not assess carry/ no-carry effects and compare addition from the perspective of brain activation during various conditions. We plan to address all these limitations in future studies.

Conclusions

Our study aimed to measure brain activation in frontal and parietal regions using fNIRS to investigate the neural correlates of exact calculation problems with two-digit numbers in different formats (word versus numerical). We found that tasks in word and numerical formats activate different areas of the brain, since these two formats of presenting arithmetical problems differ in the amount of cognitive effort required and processes involved in calculation. Our findings support domain-general theories in numerical cognition, which suggest that both domain-specific skills such as magnitude processing, and domain-general skills such as working memory, fact retrieval, and attention are involved in mental calculation. Solving of arithmetical problems presented in a word format requires several steps, including understanding the verbal information underlying mathematical relations, and transitioning to symbolic mathematical expression. This processing of numerical information is more complex, and results in higher oxygen consumption compared to solving numerical problems. We also found that the patterns of neural activation differed between individuals with low and high levels of math competencies. Low performers demonstrated right hemisphere activation, while high performers showed left hemisphere activation. Right hemisphere activation in low performers when solving exact calculation tasks in a word format might be stress-induced, as solution-irrelevant interpretations of words within a task might lead to rough semantic coding associated with the right hemisphere. We observed increased activation in the Broca’s area and left inferior frontal gyrus in low performers when solving problems in a word format compared to a numerical format. In high performers, we found increased activation in the occipi-to-temporal region, particularly in the left inferior temporal gyrus and left fusiform gyrus, when solving problems in a reading format compared to a numerical format. In summary, our findings demonstrate that the neural correlates of two-digit exact calculation in numerical and word formats differ in individuals with low and high math competencies. These results suggest that future research should consider cognitive performance when describing neurocognitive mechanisms of calculation.

Acknowledgements

The paper is part of the project no. 22-28-02030, funded by RSF (Russia).

Conflict of interests

The authors declare no conflict of interest.

Author Contributions

Conceptualization, study design and stimuli preparation: M.A.S., J.A.M. and T.V.A.; software for preprocessing and analysis: G.O.P., R.G.A.; data collection and analysis: MAS and R.G.A.; writingoriginal draft preparation: M.A.S., J.A.M. and T.V.A.; writing-review and editing: M.A.S. and J.A.M. All authors approved the final version of the manuscript for submission.