The neurocontroller for satellite rotation

Published Online March 2019 in MECS

Neurocontrol is a special case of intelligent control, using artificial neural networks to solve problems of controlling dynamic objects.

The term “neural control” was first used by one of the authors of the method of back propagation of an error by Paul J. Verbos in 1976. There are numerous examples of the practical application of neural networks for solving problems of controlling an aircraft, a helicopter, a robot car, an engine shaft rotation speed, a satellites with rotation wheels ect.

Most fuzzy logic controllers are actually proportional– integral–derivative controller (PID controllers) with the fuzzy logic used to schedule its gains. So it is actually a

PID controller, but with variable gains. For nonlinear processes, using variable gains is naturally better than fixed ones. But fuzzy logic is an “approximation” of experienced rules. It is mostly used to transform neural networks or statistical like interpolations into PID tunnings.

The main problem is in training organization on the board when the new training results are appeard [1]. The learning process can be quite long (days or weeks), but the decision process in a neural network is determined only by the number of layers (and neurons for the case of sequential processing) (milliseconds). In the neural network basis, it is possible to effectively solve the problem of approximating the function of searching for a control action in a time that is shorter or comparable to the traditional approach. In addition, it should be noted that homogeneous methods for solving heterogeneous control problems would significantly simplify the hardware implementation of the control system. Thus, neural and neuro-fuzzy control systems meet the requirements for onboard systems or satellites and form control models in a common technological key both in terms of the hardware solution and in the sense of the unity of the methods for obtaining the solution.

The purpose of this paper is the neurocontroler for attitude control: satellite rotations. The AI module, after trained for different configurations of wheels, will get commands with desired 3D rotation speeds and control the wheels to achieve the desired rotation speeds.

The novelty of the paper are modified NN Elman approach and Feed Forward NN mini-batch approach that allow us to decrease computation complexity and increase the accuracy of satellite’s model.

The paper consists of the neurocontroller classification chapter, proposed neurocontroller method, the results discussion and conclusions. The first part of paper is overview of neurocontroller types. After that, the new configuration of neurocontroller is proposed. The simulator is created for dataset creating. The results of trained neurcontroller using modified NN Elman approach and Feed Forward NN mini-batch approach are presented. In conclusion part the comparison with existing neurocontroller is given.

• ІІ.    T HE N EUROCONTROLLERS C LASSIFICATION

The methods of neural control are divided by the method of using neural networks into direct methods and indirect methods. In direct methods, the neural network is trained to directly generate control actions on an object; in indirect methods, the neural network is trained to perform auxiliary functions: identification of the control object, noise suppression, online tuning of the device in the control loop with feedback controller coefficients. Depending on the number of neural networks that make up a neurocontroller, neural control systems are divided into single-module and multi-module. Neural control systems that are used in conjunction with traditional regulators are called hybrid ones [2].

In the tasks of neural control, the black box model is used to represent the control object, in which the current input and output values are observed. The state of an object is considered unavailable for external observation, although the dimension of the state vector is usually considered fixed. The dynamics of the control object can be represented in a discrete form:

X ( k + 1 ) = Ф ( X ( k ), u ( k ) ) (1)

y ( k + 1) = ^ ( X ( k )) (2)

where X ( k ) e R^N is state of object of range N in the tact k ; u ( k ) e R^P is value of P -dimensional control vector in the tact k ; y ( k + 1) e R V is value of V -dimensional object output in the tact ( k + 1) .

The analysis of modern systems of automatic control of nonlinear dynamic objects shows that they are created as adaptive systems with feedback. This requires knowledge of the model of the control object. A well-known control system is a feedback model with real-time time-varying coefficients.

The adaptive Astrom regulator based on Lyapunov's direct method presents such type of model [3]. Fig. 1 represents the Closed Loop Control applied to Satellite using Neurocontrol.

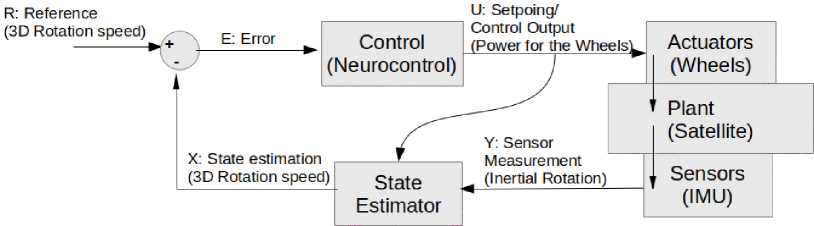
Fig.1. Closed Loop Control applied to Satellite using Neurocontrol

The use of neural network has its own specificity, which creates the corresponding requirements for the neural network architecture and its learning algorithm. In most cases, for the considered works, the neural network acts in one of the following elements (Fig. 2).

• 1.    Regulator [4].

• 2.    Models of the control object [5].

• 3.    Optimal control object filter [6].

• 4.    The regulator is compatible with another regulator: linear and built using elements of fuzzy logic [7].

• 5.    Optimization controller of another type [8].

• 6.    Classifier or system for image recognition [9].

• III.    Related Works

Inherited Neurocontrol (Neurocontrol learning based on mimic, Controller Modeling, Supervised Learning Using an Existing Controller) [10] covers neurocontrol systems in which a neurocontroller learns on examples of controller dynamics. After training, neural network accurately reproduces the functions of the input controller. Inherited neurocurrency is used for initial learning of neural network with the use of other methods for the subsequent training of the neurocontroller.

Inverse Neurocontrol. In [11], some examples of the use of an inverse model control scheme for linear systems using neural network are shown. In this approach, the formation of an inverse control object model is carried out through the training of neural network.

In the generalized inverse neurocontrol [12] it is envisaged to study neural network in off-line mode, based on the recorded trajectories of the behavior of a dynamic object. To get such trajectories on the control object as a control signal, some random processes are presented. The values of the control signals and the corresponding reactions of the object are recorded and form the learning sequence on the basis of them.

During of training, the neural network must monitor and remember the dependence of the control signal u ( k -1) on the next value of the reaction of the control object that was before in the state X ( k -1). The values of the control signals and responses of the object are recorded and, on this basis, a training sample is formed.

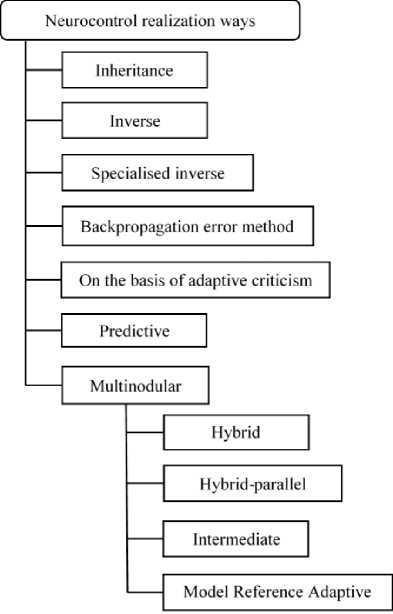
Fig.2. Neurocontrol realization ways

U = { P i , T i } M 1 : P i = [ y ( i ) X ( i - 1) ] T , T i = u ( i ) (3)

We used and desired reaction.

In the training mode neural network must find and remember the dependence of control signal u ( k - 1), in state before S ( k - 1). When the object is controlled, the inverse neuro-emulator is connected as a controller and it is receiving the rr ( k ) value from input r ( k + 1) :

rr ( k ) = [ r ( k + 1) X ( k ) ] T (4)

It is assumed that the inverse model of the control object formed during training is adequate, therefore, the control signal emitted by the neural network will ensure the object's transition to the position specified by the setpoint.

Thanks to the stabilizing feedback effect, a fairly high quality control is achieved. Known variations of general inverse control, in which, instead of the running value of the target value, the target trajectory is given in L steps ahead.

The advantage of generalized inverse neurocontrol is the training of the neurocontroller in off-line mode in the absence of an exact mathematical model of the control object.

Specialized inverse neurocontrol [13]. This type of inertia allows you to teach an inverse neurocontroller online, using the deviation error from the set value e = r - y . The neural network generates a control signal that gives the control object’s position y(k + 1). Further, we determine the error of the neurocontroller. The correction of neurocontroller weights is performed using descent method or some other gradient method. The advantage of this approach is the high quality of control compared to the generalized inverse neurorubation method. A significant disadvantage is the need to know the exact mathematical model of the control object that is required for training the neurocontroller.

The method of error transmission through a direct neuroemulator. This approach uses two neural networks [14], one of which acts as a controller, and the other - a direct neuroemultizer, trained to simulate the dynamics of the controlled object. And while learning a direct neuroemulator at the output of the control object, a random control signal u is made that changes the position of the control object y, and on the basis of such values, we create a training sample. The training of a direct neurocontroller is carried out in off-line mode. The mechanism of reverse propagation through a direct neuroemultizer implements a local inverse model of the state of the control object in the current space. Passing through the neurotransmitter, the error spreads through the neurocontroller, but now its passage is accompanied by correction of weight coefficients of the neurocontroller. The neuroemultizer thus performs the functions of additional layers of the neural network neurocontroller, in which the weight of the connections is not corrected.

Forecasted neurocontroller. In [15], an neural network speed controller with prediction is given Predictive Controller is considered. The method of training neurocontrollers, which minimizes the deviation of the current position of the control object from the specified for each step, does not always provide the best integrated control quality. The quality of work will depend on the implementation and selection of the minimization algorithm to predict the corresponding signal obtained from the control object model.

The prediction models of neurocontroller [16] minimizing the integral error functionality looks like:

L ₂

Q(k) = ^ e (k + i) + i = L

L ₂

+p^ ^(u (k + i) — u (k + i — 1))

i = 0

where e is error, p is the contribution of the control signal to the overall function Q . We make prediction to L ₂ tacts, 0 <  L <  L and start from L tact.

To predict the future behavior of the system and determine the error, a direct neuroemultier is used. It is trained for the inverse spread of the error. The peculiarity of such a method is the lack of a training controller. Its place is an optimization module that can work in real time [16]. The disadvantage of predictive model neurorization systems is its limited use in systems with fast changing dynamics, since the optimal real-time algorithm will not be able to find the best control strategy for one tact.

The methods of neutralization based on adaptive critique [17], like the system of predictive model control, choose a control signal based on estimates of the future behavior of the control system. Such a system contains two neural modules: a neurocontroller and a module of criticism. The criticism module uses the approximation of the transfer function value. The popularity of systems of adaptive criticism is due to the presence of a developed theoretical basis in the form of the theory of dynamic programming of Bellman, as well as the property of similarity to optimal or close to optimal control.

Multidimensional neurocontrol is characterized by a structure of type of expert committees [17]. For a multidimensional approach, the original task is divided into separate subtasks, the solution of which is assigned to individual modules. Systems of multimodal neurocontrol based on local inverse models consist of a large number of linear neurocontrollers and a control module. Each of the linear controllers is the neural network direct propagation of the signal, which is trained to control within the local area of the object state space.

Different methods can be used to form a neurocontroller [2]:

• •    generalized inverse neurocontrol,

• •    specialized inverse neurocontrol,

• •    method of return error transmission through a neurocontrol.

The disadvantage of such a method for training a neurocontroller is the need for a large amount of training examples distributed in the space of states of the control object.

The method of multimodal neurocontrol based on the pair of direct and inverse models [18] differs from the method of neurocontrol based on local inverse models, in which the behavior of the system is formed during training and during control is not corrected. Such a method involves adjusting the behavior of neural modules at each beat of the neurocontrol. A significant disadvantage of the multimodal neurocontrol system is the opaque procedure for separating the training sample into a sample for the study of direct and inverse neurotransmitters of different modules. Hybrid neurocontrol is based on the use of compatible neural network approach with conventional controllers, proportional–integral–derivative controller (PID controller or three-term controller) regulators or other types of controllers. The hybrid neuro-PID control [19] allows self-adjusting of the PID controller in on-line mode using neural network. Controlling using the PID controller is to minimize feedback errors. The control signal produced by the controller is the sum of the proportional, integral and differential components.

A disadvantage is the problematic evaluation of the stability of the resulting nonlinear controller. For such a method, there is a need for an analytical mathematical model of the control object.

Methods of hybrid parallel neurocontrol. In [98] parallel use of neurocontrollers with a conventional controller for the controlling of dynamic objects is foreseen. In this case, the neurocontroller and the usual controller, in the role of which, for example, PID-controller, receive identical setup values.

Hybrid parallel neurocontrol is a compromise solution for traditional neurocontrollers and transition from conventional controllers to neural network. Auxiliary neurocontrollers is relevant when it is necessary to solve additional problems that arise in the process of dynamic objects controlling. The quality of controller control can be increased and the trajectory of motion of the object smoother when using external perturbation filtering [19]. Initially, such a scheme was use in conjunction with neurocontrollers trained on the principle of general neutralization. This approach is applied to the control object with reverse dynamics in the presence of an adequate mathematical or simulation model of the control object for the training of a direct and inverse neurotransmitter.

Model of Reference Adaptive Control [20] is an option of neutralization according to the method of reverse error propagation through a direct neuroemultizer with additional introduction into the scheme of the reference model. In order to reduce the uncertainty in the control process between the object and the neurocontroller, a reference model, as a rule, a linear dynamic system of low order, which can be easily verified by analytical methods for stability [20], is introduced. The reference model is selected in such a way that the trajectory generated by it on each tread could be attainable for the control object. K. Krishnakumar et al. [20] proposed an original modification of the neutrophication with anadaptive reference model for the creation of a crashresistant control system of the aircraft. The standard model is studied in the off-line mode by minimizing the mean square error by deviating the trajectory of the motion of the control object from the target trajectory. Such an adaptive system can be considered as a normal neurocontroller of the type of adaptive criticism, which controls the combined dynamic system "PID-controller + object control."

• ІV.    P ROPOSED N EUROCONTROL M ETHOD

First, we should generate dataset for neural network training.

• A.    Simulator architecture

The class diagram for the simulating of satellite rotation for neural network education is given in Fig. 3.

Design layers:

• •    Contracts shows main entities of simulator and grants low coupling between their implementations. Contracts consists of abstractions;

• •    Core implements contracts. It contains primary physical model and Simulation entity.

• •    Satellite simulation extends Core with a dynamic of reaction wheel and satellite.

Entities:

• •    Point – provides an abstract point for further implementations;

• •    MassPoint – point with mass and movement vector;

• •    ForcePoint – predetermines point of attachment of force and current vector of force;

• •    Object – provides enumeration of points, which interact with each other;

• •    ReactionWheel – inherited from MassPoint instances, is used for changing rotation speed of satellite by changing its angular momentum;

• •    Satellite – inherited from Object, provides simulated Satellite of arbitrary form, which moves and rotates using thrusters (ForcePoint) and reaction wheels.

  

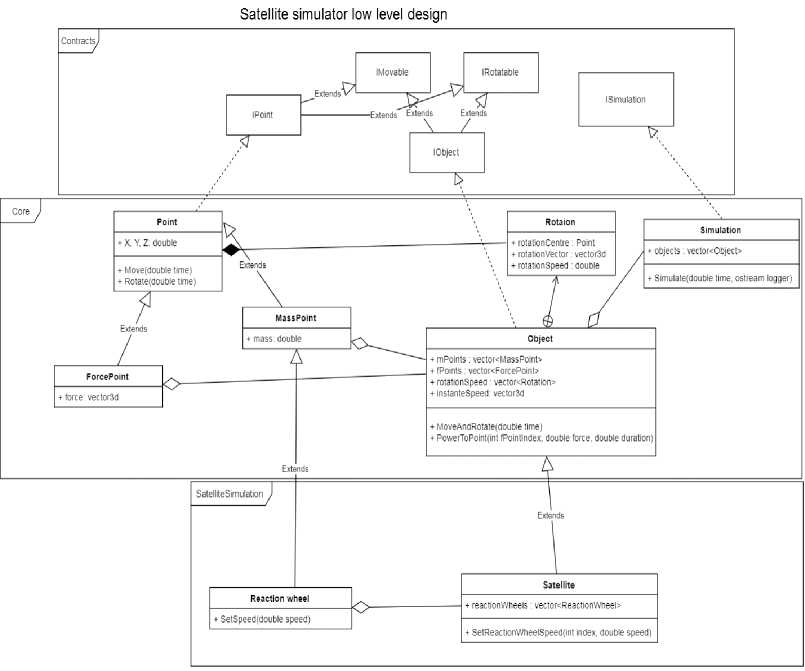
  Fig.3. The simulator class diagram

  
  

Simulator provides enumeration of Object instances and configuration of scenario of their behavior.

Point class is a generalization of 3D point, which can be moved or rotate. Logic of this class is used in other points (MassPoint, ForcePoint etc.).

Instance movement of Point is rather a simple implementation. We just have to set a vector of current instance speed (SetInstanceSpeed method) and use Move method to move it. Notice that all vector values are from Eigen library this implementations use vector3d class.

Rotation movement is more complicated than the previous movement. The point to be rotated must have axes of rotation and its rotation speed. Rotation axes is a line, which can is set as a guide vector of the line and point, which belongs to the line. The point P will be rotated around the axes after its rotation speed and rotation axes are set and Rotate method called.

As far as it concerns rotation speed, it is measured in radians per second, if it is positive point rotates clockwise, else anticlockwise.

When we use this type of motion, we simulate moving of point by vector of speed. In further implementations of simulation’s core, it is used to move other objects.

Parameters of RotatePoint:

• •    point – point to rotate,

• •    axesVector – vector of rotation axes,

• •    axesPoint – point which bellows to rotation axes,

• •    angle – angle for rotation[rad].

MassPoint class inherits implementations of Point so motion of MassPoint is same as in Point. However, there is mass [kg] MassPoint added which is used in Object implementation to define its mass and inertia.

Object class is a virtual model of material object, which is represented as array of mass points.

Object obeys the laws of mechanics and non-relativistic kinematics. Implementation of its behavior we use to create more complicated physical systems, such as satellite, for instance.

• B.    Neurocontoller implementation using NN Elman

The neurocontroller for the control loop is based on the Elman network, which consists of the input, hidden and output layers. Elman's neural network is one of the types of recurrent networks, which is derived from the multilayer perceptron by the introduction of feedback, only the connections go not from the output of the network, but from the outputs of the internal neurons. This allows you to take into account the history of observed processes and accumulate information to develop the correct management strategy. These networks can be used in the control systems of moving objects, because their main feature is memorization of sequences. Unlike other types of recurrent neural network (NN), such as Hopfield, Hemingham, Jordan, additional lines of dynamic delay from the output of neural network to its input were introduced into the structure of NN Elman [21 – 22].

The modified algorithm for neurocontroller using NN Elman training consists of the following steps:

Step 1 . At the initial time t = 1, all hidden neurons are set to zero - the initial value is zero.

Step 2 . We send the input value to the network, where it is directly distributed in the neural network.

Step 3 . According to the training of the neural network by the chosen Fletcher-Rives algorithm, which, in comparison with the gradient-descent algorithm, governs the convergence speed not only by setting the speed parameter, but also corrects the step size for each iteration. So, achieve the set value of the error we perform for the minimum number of iterations.

Step 4 . We set t = t + 1 and carry out the transition to Step 2. We will continue to train the neural network until the total mean square error of the network is of the least value.

The network final error depends on the number of hidden neurons and the number of training points. In order to achieve a given precision, the larger the training set, the greater the number of hidden neurons. Training was carried out by generating positions from IRotatable. The neural network used in controller design is threelayered.

Starting with 8 neurons and 256 training points, the required output error was reached with 24 neurons, and the learning process succeed with only 2576 points [22 -24]. In this network, the unknown parameters are considered as network’s weights, which are updated over the time and are converged to their true values.

Z i = f (Y i ) = f ( ^ i + S ( X j , W ) )          (6)

where, U is output signal of neuron i , f is activation function, Y is average sum of input signals, X is signal j of hidden layer, W is weight [23 – 26].

Weight updates are be done using the error between output of the network (estimated control torques) and the control torque generated by feedback linearization controller. The back propagation update law is considered as follow:

A W = -n — d W

where, J is the cost function of neural network which defined based on the difference between the estimated torque and real torque control.

• C.    Neurocontoller implementation using mini-batch gradient descent

For the design of adaptive-neural network control, first, the feedback linearization controller is designed and then a neural network is used to estimate the system’s uncertainty. To estimate the unknown parameters of the system, the multilayer neural network with back propagation update law is used. Simple structure and small number of parameters to be adjusted, is the main advantage of the designed neural network.

Generalized inverse learning presents some negative properties when the training is performed with the real system, as there is no guarantee that the system output covers totally the state space. Of course, this problem will not happen in case of a numeric simulated system. Indirect model presents some instability during training, depending on the system dynamics. Specialized inverse method requires a network direct model in order to establish a relation between the direct model output error and the control network output error. In a simulated system, nevertheless, specialized and generalized methods are equivalents and so the results presented here were obtained with the generalized inverse model, as shown in Fig. 4.

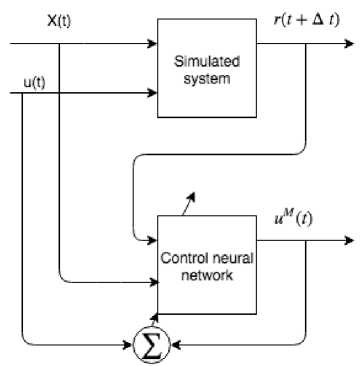
Fig.4. Control network training model

Inputs to the control network are the state (speed of each rotation wheel) at time t and the propagated speed at time t +∆ t . The output is the control signal (torque). The neural network structure looks like this:

sigmoid activation function,

• •    Output layer – n neuron with predicted energy level, where n is equal amount of rotation wheels,

• •    The bias is used too.

• •   Input layer – 3 neurons (for rotation speed by

x,y,z),

• •   Hidden layer – fully-connected neurons with

The controller class diagram is given in Fig. 5.

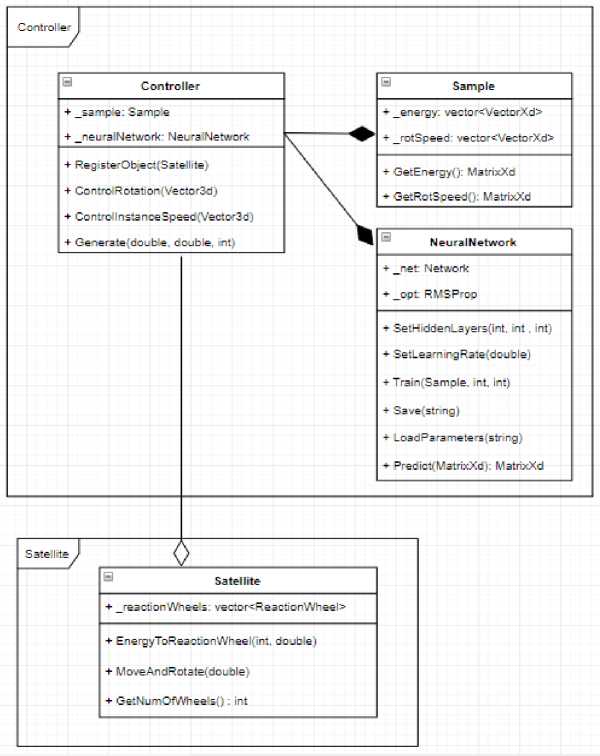
Fig.5. The controller class diagram

• V . Results

The process of NN Elman training lasted 154 epochs.

The training parameters are as follows (Fig. 6):

• •    the limit value of the learning target goal - 10^-5;

• •    minimum gradient value min_grad - 10^-10;

• •    maximum number of epochs training - 1000.

  

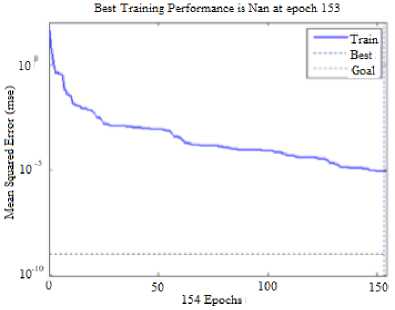
  Fig.6. Training schedule of NN Elman

  
  

Error value estimating is demonstrated in Fig. 7. We compared error rate for tuned PID controller with Ts=1 and Ts=2 and for modified NN Elman with Ts=1 and Ts=2. The modified NN Elman (proposed approach) gives the smaller error rate for both times.

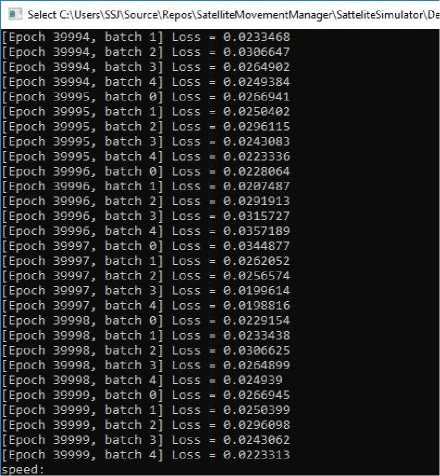
Fig.8. Trained neural network parameters

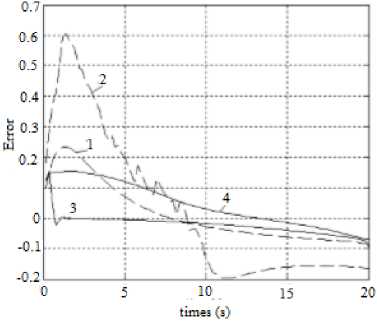
Fig.7. Error while adjusting, sine trajectory: 1 - tuned PID controller, Ts = 1; 2 - tuned PID controller, Ts = 2; 3 - modified NN Elman, Ts = 1; 4 - modified NN Elman, Ts = 2

In addition, we create fully-connected NN using minibatch gradient descent. Mini-batch gradient descent is typically the algorithm of choice when training a neural network and the term stochastic gradient descent usually is employed also when mini-batches are used. The best result can be achieved by using this parameters:

NUMBER_OF_SAMPLES1000

NUMBER_OF_HIDDEN_LAYERS1

HIDDEN_LAYERS_LENGTH15

LEARNING_RATE               0.0007

BATCH_SIZE200

EPOCH40000

NORMAL_DISTRIBUTION_MEAN0

STANDARD_DIVIATION0.01

RANDOM SEED40

Network results are given in the Fig. 8.

As you can see, the error rate is appr. 0.02, that is smaller than in previous NN configuration.

The advantage of this NN configuration are:

• •   reduce the variance of the parameter updates,

which can lead to more stable convergence;

• •   can make use of highly optimized matrix

optimizations common to state-of-the-art deep learning  libraries  that make  computing the gradient  w.r.t. a  mini-batch  very efficient.

Common mini-batch sizes range between 50 and 256, but can vary for different applications.

The paper presented a comparison of a neural network attitude and conventional PID controllers. Neural network acting as a nonlinear system control has some intrinsic advantages that can be exploited in further studies. The class diagram for simulator was build.

Two types of NN configuration were created and trained.

As the output accuracy of NN Elman was a fraction of the value 0.1, training was completed even with 24 hidden neurons. The indicated graphs of the comparator work of the controller indicate that the change of the parameter of the controlled object does not significantly affect the quality of the control in the circuit with the NN, and the PID-regulator tuned to the sinusoidal signal, with a significant error, runs the pulse change of the input signal.

As the output accuracy of NN with mini-batch gradient descents was a fraction of the value 0.02, training was completed even with 15 hidden neurons.

The result of system error is too small, that is why the AI module, after trained for different configurations of wheels, will get commands with desired 3D rotation speeds and control the wheels to achieve the desired rotation speeds.

• [1]    Khuntia, S. R., Mohanty, K. B., Panda, S., & Ardil, C. (2009). A comparative study of PI, IP, fuzzy and neuro-fuzzy controllers for speed control of DC motor drive. 16

• [2]    Gundy-Burlet, K. (2004). Augmentation of an intelligent flight control system for a simulated C-17 aircraft. Journal of Aerospace Computing, Information, and Communication , 1 (12), 526-542

• [3]    Parks, P. (1966). Liapunov redesign of model reference adaptive control systems. IEEE Transactions on Automatic Control , 11 (3), 362-367

• [4]    Bouchard, M. (2001). New recursive-least-squares algorithms for nonlinear active control of sound and vibration using neural networks. IEEE Transactions on Neural Networks , 12 (1), 135-147

• [5]    Ku, C. C., & Lee, K. Y. (1995). Diagonal recurrent neural networks for dynamic systems control. IEEE transactions on neural networks , 6 (1), 144-156

• [6]    Ito, K. (2000). Gaussian filter for nonlinear filtering problems. In Decision and Control, 2000. Proceedings of the 39th IEEE Conference on (Vol. 2, pp. 1218-1223). IEEE

• [7]    Vasičkaninová, A., & Bakošová, M. (2009). Neural

network predictive control of a chemical reactor. Acta Chimica Slovaca , 2 (2), 21-36

• [8]    Sahu, A., & Hota, S. K. (2018, March). Performance comparison of 2-DOF PID controller based on Mothflame optimization technique for load frequency control of diverse energy source interconnected power system. In Technologies for Smart-City Energy Security and Power (ICSESP), 2018 (pp. 1-6). IEEE.

• [9]    He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).

• [10]    Ellery, A. A. (2017). Space Exploration Through SelfReplication Technology Compensates for Discounting in Net Present Value Cost-Benefit Analysis: A Business Case?. New Space , 5 (3), 141-154.

• [11]    Izzo, D., Simões, L. F., & de Croon, G. C. (2014). An evolutionary robotics approach for the distributed control of satellite formations. Evolutionary Intelligence , 7 (2),

107-118

• [12]    Briggs, F. C. (2016). Soft Computing in Aerospace. In AIAA Infotech@ Aerospace (p. 0483).

• [13]    Tamayo, A. J. M., Bustamante, P. V., Ramos, J. J. M., & Cobo, A. E. (2017). Inverse models and robust parametric-step neuro-control of a Humanoid Robot. Neurocomputing , 233 , 90-103.

• [14]    Gleue, C., Eilers, D., von Mettenheim, H. J., & Breitner, M. H. (2017). Decision support for the automotive industry: forecasting residual values using artificial neural networks.

• [15]    Kar, S., Das, S., & Ghosh, P. K. (2014). Applications of neuro fuzzy systems: A brief review and future outline. Applied Soft Computing , 15 , 243-259.

• [16]    Wang, J., Zheng, H., Li, Q., Wu, H., & Zhou, B. (2015, October). Prognostic for on-orbit satellite momentum wheel based on the similitude method. In Prognostics and System Health Management Conference (PHM), 2015 (pp. 1-5). IEEE.

• [17]    Lendaris, G. G. (2009, June). A retrospective on adaptive dynamic programming for control. In Neural Networks, 2009. IJCNN 2009. International Joint Conference on (pp. 1750-1757). IEEE.

• [18]    van der Smagt, P., Arbib, M. A., & Metta, G. (2016). Neurorobotics:  From vision to action. In Springer

  Handbook of Robotics (pp. 2069-2094). Springer, Cham.

• [19]    Dias, F. M., & Mota, A. M. (2001, June). Comparison between different control strategies using neural networks. In 9th Mediterranean Conference on Control and Automation, Dubrovnik, Croatia . 1-12.

• [20]    Steinberg, M. L. (2001). Comparison of intelligent, adaptive, and nonlinear flight control laws. Journal of Guidance, Control, and Dynamics , 24 (4), 693-699

• [21]    Boyko, N., Sviridova, T., & Shakhovska, N. (2018, June). Use of machine learning in the forecast of clinical consequences of cancer diseases. In 2018 7th Mediterranean Conference on Embedded Computing (MECO) (pp. 1-6). IEEE

• [22]    Shakhovska, N., Vovk, O., Hasko, R., & Kryvenchuk, Y. (2017, September). The Method of Big Data Processing for Distance Educational System. In Conference on Computer Science and Information Technologies (pp. 461-473). Springer, Cham.

• [23]    Kryvenchuk, Y., Shakhovska, N., Melnykova, N., &

  Holoshchuk, R. (2018, September). Smart Integrated Robotics System for SMEs Controlled by Internet of Things Based on Dynamic Manufacturing Processes. In Conference on Computer Science and Information Technologies (pp. 535-549). Springer, Cham.

• [24]    Dhanya, K. M. (2017). Dynamic Vehicle Routing Problem: Solution by Ant Colony Optimization with Hybrid Immigrant Schemes. International Journal of Intelligent Systems and Applications, 9(7), 52.

• [25]    Yang, B., & Cao, D. (2009). Action-dependent adaptive Critic design based neurocontroller for cement precalciner kiln. International Journal of Computer Network and Information Security, 1(1), 60.

• [26]    Albagory, Y., Al Raddady, F., Aljahdali, S., & Said, O. (2014). Innovative large scale wireless sensor network architecture using satellites and high-altitude platforms. International Journal of Wireless and Microwave Technologies , 4 (2), 12-19.