The rate of convergence of hypersingular equations numerical computation

A number of diffraction problems on an unclosed cylindrical surface, on a. rotary surface, are described by a. hypersingular equation of the form is defined as:

( Au ) ( т ) + a ( Lu ) ( т ) + в ( Ku ) ( т ) =

= ¹    / u ( t ) ^d l,    ' dt +

π ∂τ         ∂t |τ - t|

- 1

+ a

I u ( t )

In

|τ

-

dt + в

I^K ( ^т , t ) ^u ( t ) ^dt = ^f ( ^т ) ,

- 1 < т <  1 ,

where both a and в ^are constant values, and the core of K ( т/t ) is a continuous function.

The theory of the (1) equation is described in [1] and it is based on the properties of a hypersingular integro-differential operator is defined as:

⁽ Au ) ⁽ т⁾ = -l" [ u ⁽ t In r-^dt.                     (2)

π ∂τ ∂t |τ - t|

- 1

The theory, has described paper [1], also proved that the A operator is a symmetric positive-definite operator in a L2 [ — 1 , 1] Hilbert space and has a dense domain of definition. The inverse operator has defined by the following ecpiations:

( A ^{- 1} f) ( T ) = ¹ [ f ( t ) In -----             T= ₂ dt             (3)

nJ         1 — Tt + v 1 — т 2\ 1 — t ²

- 1

and it is not only terminated, but it is also completely continuous operator in the L2[—1, 1] area. For any B operator that is terminated by the L2 [—1, 1] area, there is T = A-1B operator, that completely continuous in the HA energy space of a symmetric positive-definite A operator. Multiplying both sides of equation (1) by an A-1 operator, we obtain u (т) + a (A-1 Lu) (т) + в (A-1 Ku) (t) = A-1 f.                  (4)

Equation (4) is the Fredholm equation of the second kind in the H A energy space.

1.    Estimation of the Rate of the Convergence of the Reduction Method

To understand the important ideas we introduce the function system фп (т) = \ — sin [n arccos (т)] = \ —V1 — т2 Un (т), n = 1,2, 3,..., πn                πn

where (•, •) means the scalar multiplication in L2[—1, 1]. a,nd U (т) are Chebyshev polynomials of the second kind: U1 (т) = 1, U2 (т) = 2t, U3 (т) = 4т2 — 1, etc. This functions system forms the basis of space HA [1]. It is complete and orthonormal and it’s defined as

[ ф п , ф т ]

⁽ A ^ф n , ^ф т )

1 , m = n, 0 , m = n,

where [ •, • ] is a scalar mu implication in H A space. Now we reduce equation (1) to an infinite system. For this, we represent the solution of equation (1) in the following form:

+∞ u (T) = 52 Спфп (T) .

n =1

We substitute the (7) equation into (1) and multiply scalarly in L ₂[ — 1 , 1] space by the ф 1

ф2, . . - фп, equations: ... basis functions. As a result, we obtain a following system of linear algebraic +∞         +∞ cn + a     cmLmn + в     cmKmn   fn, n 1, 2, . . . , n, . . .              (8) m=1          m=1 where

L mn

— ^{( Lф} m , ^ф п ) , K mn — ^{( Кф} т , ^ф п ) , f n — ⁽ f, ^ф п ) ■

Because equation (4) is a Fredholm equation of the second kind, system (8) is a Fredholm system of the second kind in the 1 ₂ space of quadratically summable sequences too. To solve the system, we apply the reduction method [2, p. 534], i.e. we replace the infinite system by the corresponding truncated system as follows:

N

N

c n + a

'^c m ^L mn

+eE

^c m K mn

— f n ,n — 1 , 2 ,...,N.

m =1

m =1

Let set the problem to estimate the difference between the c — ( c 1 , c 2 ,...,c n ,... ) exact solution of system (8) and the C — ( C 1 ,c ₂ ,...,c _N , 0 , 0 ,... ) approximate solution, i.e. solution of the system (9), considering the fact that both c and C belong to the same space 1 ₂. As described in [2, p. 536], we have the following estimate:

ll ^c - ^c || < C i

[ + ^ + ^       2         + ^       2

E Ela.k12 + C2 E Ifil2 ■ i=N +1 k=1                i=N+1

The first term of sum (10) is determined by the system matrix, and the second by the right-hand side.

In the diffraction problem on a strip, for example, the right-hand side is given in the follows form:

f ( t ) — exp ( iaT cos ф ) ,                               (11)

where a is an electric half-width of the strip, ф is an angle of incidence. Now we find the right-hand sides, confining ourselves to even functions, like the standard integral [3]

^f 2 i- 1

J ф ₂ i- 1 ( t ) exp ( iaT cos ( ф )) dT —

- 1

( - 1) i— 1 V 2 n (2 i - 1) J ² i — ^{1 (} a Щ ^ф >> . a cos ( ф )

The right-hand sides are expressed in terms of Bessel functions; decrease rapidly, exponentially [3]. Therefore, in this case the rate of convergence in the method of reduction is determined only by the system matrix. Consider the system matrix, confining ourselves to the case в — 0. Matrix elements of the integral operator L we can be found analytically. Using the follows identity [3]

1+

In — C + / COSHL-H-ldx + [ cos|x (T — t>1dx, C — 0,5772, |τ -t|                       xx

integrals of the form (12) and the follows standard integral [3]

j x^{a - 1 J m} ( ex ) J ( ^cx ) ^{dx —}

— 2 ^{a - 1}

c

α

Г(1 — a )Г(( m + n + a ) / 2)

Г(1 + ( n — m — a ) / 2)Г(1 + ( m — n — a ) / 2)Г (1 + ( m + n — a ) / 2) ’

we find the matrix elements of an integral operator L with a logarithmic singularity in the core

(Ьф2i-1 ,ф2j-1 )=  ln2+ , if i = j = 1,(15)

2g

^{( Ьф} 2 i- 1 ^,ф 2 j- 1 ) = g i ( i - i) , if i = j >  ¹ ,

,               x             \/(2i - 1) (2j - 1).

^{( Ьф} 2 i- 1 , ^ф 2 j- 1) = - . / . -W • । ■---- 1 W i ¹--- , ^ ^j = i — ¹

4( i + j )( i + j - 1)( i + j - 2)

^{( Ь} ф 2 i- 1 ,ф 2 j- 1 ) = ⁽ ф 2 i- 1 ^,Ь ф 2 j- 1 ) ,

(Ьф2i-1, ф2j-1) = 0, if |i - j | > 1.(19)

Thus, the matrix of an integral operator L has a remarkable property - it is three-diagonal. According to the analysis of the rate of convergence, this matrix is close to the diagonal matrix, in which all elements except the main diagonal are equal to zero.

From inequality (10), taking (16) - (19) into account, after simple calculations, we obtain the following theorem.

Theorem 1. There is an estimate of the rate of convergence of the approximate solution to the exact follows solution

^^{C - C} ^ = O ( N^N ) '                        ⁽²⁰⁾

Table 1 demonstrates the efficiency - fast convergence of the reduction method at the normal incidence of an electromagnetic wave. The results obtained with N = 5 and N =10 completely coincided.

Table 1

The values of the solution at zero depending on the number N of basic functions a = 1 /п, в = 0, ф = п/ 2

N	uN (0)	N	uN (0)	N	uN (0)	N	uN (0)
1	0,6679544	2	0,6550782	5	0,6553978	10	0,6553978

• 2.    Model of the Delta Function in the Theory of Vibrator Antennas and Its Approximation

In this subsection we construct a function f ( т ) for which the reduction method products poor convergence; does not work. In problems of excitation of vibrator antennas, the primary field is localized in a small area. To simplify the calculations, the primary field was represented in the form of the Dirac delta function discussed in the monograph [4]

f ( т ) = 5 ( т ) .                                        (21)

We note that the function (21) does not belong to the space L2[ — 1,1], but a completely continuous operator A1 is defined on a wider space [5]. Therefore we can find follows solution

( A ¹ 6 ) ( т ) = — In

τ

1 + V 1 — т ²

This function is unlimited and, therefore, the delta function model is not applicable for the strict solution of the ecpiation, because in the process of solving it is necessary to find a quantity that, in physical sense, is finite. Consider a function that belongs to the space L2(—1, 1) and approximates the Dirac delta function in the sense of generalized functions f * (T) = {

£, V" । ^ ^E, 0 , |т| > E.

Consider right-hand sides of system (8) for the function 6 ( т )

^f 2 i- 1 = j ф 2 i- 1

- 1

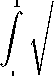
- 1

2           „        X          Z M X ,

—-------- sin [(2i — 1) arccos (т)] 6 (т) dт = n (2 i — 1)

= У Пу— ) ^{( — 11}

i- 1

.

And now let us turn to the series

[ E if i tl 2 , i = N +1

of convergence rate (10) entering the estimate. When we substitute (24) this, we obtain, as we would expect, a divergent series. After replacing, the delta-function by f^e ( т ), the corresponding series will converge. However, the value of the series will depend on e, as e decreases, it will grow and, apparently, one can not obtain a uniform estimate, which does not depend on e . As a consequence, we should expect a slow convergence of the reduction method. Table 2 summarizes the values of the solution of the equation u^N (0), obtained by the reduction method.

Table 2

The values of the solution at zero depending on the number N of basic functions a = 1 /п^ в = 0

N	E = 0 , 1	E = 0 , 01	N	E = 0 , 1	E = 0 , 01
1	0,4319895	0,4326044	10	1,003179	1,096826
2	0,5969654	0,6003707	20	1,028233	1,313883
3	0,7122543	0,7206242	40	1,026874	1,521940
4	0,7937296	0,8091264	80	1,014211	1,695528
5	0,8543462	0,8787146

As follows from this table, there is no internal convergence, stabilization for e = 0 , 01. We gave an example for which the method of reduction "does not converge".

3. Analytical Modification of the Reduction Method

Consider another method for solving system (8). We represent the solution system in the form of a sum of two terms

of the

c n    c n ^{+ f} n

and substitute it into system (8). As a result, we obtain a new system of the form

+ ^         + ^

c n + а У ^C‘m L mn ⁺ T V- = ^

where

f ∗

n

-α   f _n L _mn

-

+ ^

^в      f n K mn , ⁿ    1 , ² , . . . ,n, . . .

Let’s show that the right-hand sides of (28) fast enough decrease independently of the

right-hand side of the original equation. By the Cauchy - Bunyakovskii inequality we have

Ifn| = [A-1 f^n] < [A-1 f] [фп] = [A-1 f] = C, where [ • ] is the norm in the energу space. Further, setting в = 0 from (28). we have

+oo

|f n^∗ | ≤ |α|C      |L mn |.

m =1

Hence, taking (16) - (19) into account, we obtain the following theorem.

• Theorem 2. There is an estimate

1 fNl= "' N^ ■

The system (27) will also be solved by the reduction method. After solving this system, taking (26) into account, we find an approximate solution of system (8) in the form

+re            N             + reN uN (T) = ^ fnФn (T) + ^ СПФп (T) = ^ (f, Фп) Фп (T) + ^ сПФп (T) • n=1            n=1             n=1

The first term in (30) can be turn into the integral [1], it exactly corresponds to the analytic inversion of the hypersingular operator A. As a result, we obtain the final formula for the approximate solution

• 1    1              T -1

4.    Applications of the Modified Method of Reduction

u (t) = -  f (t)ln -—_ Гл—2 tt^ dt + 52 спфп (t) •

П J1         1 - Tt + V1 - T2 <1 - t2

In concluding of this section, we present the results of the solution of system (8) also for the right-hand side f ( t ). given by formula, (23). The results obtained for u N (0) by formula. (30) are summarized in Table 3. The result in Table 3 demonstrate us reliable internal convergence for different values e.

Table 3

The values of the solution at zero depending on the number N of basic functions a = 1 /п, в = 0

N	Е = 0 , 1	Е = 0 , 01	N	Е = 0 , 1	Е = 0 , 01
1	1,067948	0,4154451	10	1,013074	1,744628
2	1,023392	1,800810	20	1,013007	1,744315
3	1,017207	1,756401	40	1,013016	1,744242
4	1,014998	1,749384	80	1,013016	1,744227
5	1,014066	1,747963

• 1.    We have considered the case when в = 0. However, this does not detract from the generality, for example, in the theory of diffraction the nucleus K ( t, t ) is continuously differentiable. The elements of the matrix K mn decrease rapidly with increasing m or n.

• 2.    An operator M of a more general form can be added to the initial equation. It is important that an operator of the form A ¹ M remains completely continuous in the energy space H A of a symmetric positive-definite operator A. In fact, equation (4) can be written laconically in the form u + Ku = g. This is the Fredholm equation of the second kind in H A space. Above we have analyzed the case of poor convergence of the reduction method, when the right-hand side is localized in a small area. The reason for the poor convergence is that the function g decomposes into a slowly convergent series. After replacing u = g + v. we obtain an equation of the form v + Kv = -Kg relative to v. The operator K. as completely continuous, smoothes out the function g. accelerates the convergence of the series for a function g over an orthonormal basis. Therefore, the modified method of reduction developed in this paper is universal.