The search solutions in military events

In 1956, the journal of the American Mathematical Society [1] published a short article entitled "Lost at sea" which proposed 3 problems by the famous mathematician Richard E. Bellman.

The first problem proposed by Richard E. Bellman was the theory to determine the pattern of the curve with the shortest length among all the search curves. The problem was solved by John R. Isbell in 1957 [2], and solved again by B. Glass in 1961 [3] by replacing the straight shore mainland with an island with radius S. Khaltar D. expanded and solve these problems in various ways in his works by connecting with nomadic, pastoralists and geological prospecting activities [4].

This study shows the search solution identifying enemy front line and firing position [5]. This is John Rolfe Isbell and Glass J’s search solution extension model that used the extreme point theory and a method of mathematical analysis to find solution.

This search solution is identify the ob ject that the position is uncertain, but on the line, in other words to evaluate averages of the mathematical length of the curves that certainly meet the object along those curves from the given point.

• 1    Search problem

  In 1956, in the American mathematical journal, the famous American mathematician P. Bellman had proposed military search solution that solved soldier’s lost in the ocean at night.

"For the soldier who lost alone in the ocean, he knows only the shoreline is straight and about 1 mile away, but there is no information about where the direction is. Find the shortest way that certainly leads to the land."

Figure 1 shows incomplete search solution by I.R Isabell in 1957.

W p К a

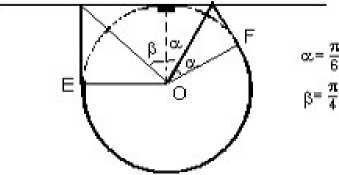
Figure 1. The shore of the mainland is undoubtedly present in the shore the shortest OKFEW curve format.

To get the shortest length of the curve, draw a certain tangent line a in the circle C (0 . 1) . Then the curve runs along the segment OK and the tangent KF , which makes an angle of ^π ₆ with the perpendicular OP drawn to the tangent from the center 0 of the circle. Then proceed along the FE curve of ⁷ ₆ ^π , and eventually ends up in the EW segment. Then OKF EW curve length

d (2 n ) = V 3 +—-—+ 1

had been obtained by Isbell’s idea.

In 1961, Glass B replaced the solution by Bellman P with island with straight shoreline radius. In his works, D.Khaltar expanded and resolved the solution related to that soldier who lost in the sea in various ways in connection with nomads, herdsmen, border guards and geological exploration.

• 2    Proposed method

  • 2.1    Mathematical model of identifying enemy front line

Consider that enemy front line is straight shaped and night reconnaissance team which is supplied with communication tools is responsible for identify as soon as possible. If the enemy front line position is known, 1 km away and in the angle of 0 < a <  2 n , then consider identifying enemy position and find the shortest way of searching to report headquarter that is located at the point "O".

First of all, take a look at our proposed solution at a — 2 n , which is overlapped with the idea of P.Bellmann. In practice, the facilitator of the research study has proposed that the shape of the curve with the shortest length is similar to Isbelle’s search curve shape (Figure. 2.a) when α is enough ( a 2 < a <  2 n ), the curve is made of two segments when a i < a < a 2 , and when 0 < a < a i , it is segment (Figure. 2.b). Then we have formulated the following.

• Theorem 2.1.

  a.

  
  

When a2 — 5П < a < 2n , the minimum length of the curve OKFEW consists of the segment OK that reflects on the angle π3 to edge tangent, the tangent KF that bounces with the angle π3 , the arc FE with the length α - 56π , and the tangent EW perpendicular to the front line. The formula of the curve length:

d ( a ) — V3 + a — — + 1

• b.    When ² ₃ ^π ≤ α ≤ ⁵ ₆ ^π , the curve OKF with minimum length consists of the segment OK that creates the angle α - ^π ₂ to the tangent a , and the segment KF that creates the angle α - ^π ₂ to the tangent a from the point K and the segment KF that is perpendicular to the tangent b . In this condition, the minimal length of the searching curve OKF is:

d ( a ) — 1 + c " ^{— П)} — cos a cos a

• c.    When 0 <  a <  27 — a i , search curve with the minimal should be the segment OK which ends at K point of a and b tangents intersection. Fol lowing is shown formula:

  d ( a ) — |OK| —

  
  

  cos 2

  
  
  
  
  

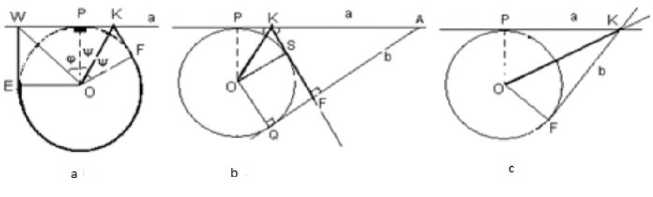
Figure. 2. The change of search curve with minimum length depending on α angle

Proof. If number α is close to 2 π , the minimum shape of the curve consists of the segment OK that reflects on the a tangent, the tangent KF that reflects from K to F on the curve C (0 , 1) and the arc FE , where the tangent EW is perpendicular to an a tangent. If the angles ∠ KOF = ψ , ∠ EOW = φ , the length of the curve is formulated as follows:

d ( ψ, φ ) =     + tan ψ + α - 2 ψ - 2 φ + tan φ,

0 < ψ < ^π₂, 0 < φ < ^π₂.

expressed by the formula. Since (1) is a strictly convex function

∂d ( ψ, φ )        ∂d ( ψ, φ )

_∂ψ = 0 , _∂φ = 0

conditions are met. 0 < ψ ^∗ <  ^π ₂ , 0 < φ ^∗ <  ^π ₂ if find ( ψ ^∗ , φ ^∗ ) , we can determine the search curve with minimum length.

∂d ( ψ, φ ) ∂ψ

sin ψ 1

cos ² ψ    cos ² ψ

- 2=0

∂d ( ψ, φ ) ∂φ

1 cos ² φ

- 2=0

The answer to (3) will be φ ^∗ = ^π ₄ . Formula (2) will be shaped as follows

2 sin2 ψ + sin ψ - 1 = 0

If sin ψ = x , (4) it changes to square formula

2x2 + x - 1 = 0

The answer will be:

- 1 ± ^√ 1 + 8    - 1 ± 3

x1;2 =      4      =

Only positive answer is x = 2 or ^ = ⁿ . curve is

The minimum length of the search

d ( a ) = 3+ + a

-

5 n

--+ 1 .

When a = 5 n , the F = E and KFW is equal to a line perpendicular to the line b from point K (Figure. 2.b). Thus, when 2 n >  a >  5П , the FE arc exists. Now we have proved the first part of the theorem.

If α is less than ⁵ ₆ ^π or close to it, it is clear that the shortest curve OKF consists of two lines OK touched on straight line a and the line KF touched on straight line b . Consider A is the intersection point of the lines a and b . Then, for the shortest length curve OKF , which extends from points F and 0 to point K on a line a , the angles Z PKO and Z AKF should be equal according to the law of reflection. Here OP is the perpendicular from 0 to the a line. On the other hand, it is obvious that the shortest length of the line connecting the point K and line b is the perpendicular line KF , which satisfies the condition Z KFA = П . Draw OS perpendicular from the point 0 to KF . The following formulas can be easily checked.

Z KAF = n - a, Z PKO = Z AKF = ^П - ( n - a ) = a - ^П,

ZPOK = П - (a - П) = n - a, |OK| =---- =—

2          2 ’          , 1     1    cos(n - a)cos

ZKOQ = a - (n - a) = 2a - n, lKFI = 1 + '        ", |OK| + |KF| = -+1 +'

cos a                      cos acos

Where Q is the base point perpendicular to line b , from point 0 .

cos(2a - n)  = -1

cos a or a = 2n, meaning the length of the KF zero (Figure. 2.b).

• a.    At a = 5 ^ , perpendicular KF is tangent circle C (0 , 1) at point S .

• b.    At a = 2ⁿ , the points K, F and A coincide.

• 2.2 Identifying and destroying firing point of the enemy as quickly as possible

From here we get a i = 2 П and the theorem is proved

Identifying and destroying firing points of enemy with incomplete location information often occur during military operations. Let’s consider that we have position information about enemy as follows. The position is located at a distance of 1 + S from our position within the sector forming an angle of 0 < a <  2 n .

Here, S >  0 is the maximum distance at which an armed reconnaissance group can completely destroy the ma jor enemy fire. In other words, it is enough that reconnaissance group is placed within S range from firing position of the enemy. In 1959-1961, that kind of problem is proposed by Glass Bellman and he considered that coast curve with the minimum mathematical expectation (average length) is as a straight coast and formulated the problem of quickly reaching the coast of a circular island of radius S and solved solution of the problem. The formula is expressed as follows. "For a soldier who lost at sea at night, if he knows that a circular island of radius S is 1 mile from him, but does not know the exact direction of its center, find the shortest search curve that will surely reach the shore of the island!" As S → ∞ , this problem shifts to problem by Isbell we discussed in the previous section. However, in this case, these problems overlap with a = 2 n . In this case, search curve with the shortest length is shaped in OKFEW and it is shown in Figure. 3.

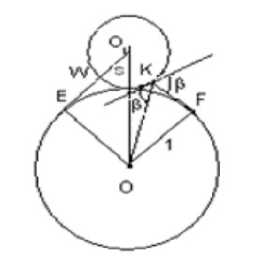
Figure. 3. The shape of the OKF EW curve for the shortest length search

In other words, starting from the point O along the segment OK , it goes along the tangent KF drawn to the circle C (0 , 1) . Here, K E C ( O i , S ) , F E C (0 , 1) and segments OK and KF have the same assumption в >  0 . It follows from the fact that among the curves with general points to the circle C ( O i , S ) connecting the points O, F outside the circle C ( O i , S ) , the shortest length is the reflection curve. J.Glass proved that the angle в ( S )

satisfies the following equation.

• ^ (1 — sin ² 2 в ) = 4 sin ² в • cos в (2 cos в - 1)              (6)

As mentioned in the previous paragraph, the following assumptions can be made for curves with the shortest length. According to the assumptions, 0 < a i ( S ) < a ₂ ( S ) <  2 п are found and the following condition is fulfilled.

• a.    When a ₂ ( S ) < a <  2 n condition is fulfilled, the shortest search curve is perpendicular EW to the segment OK , the tangent KF , and the arc FE E C (0 , 1) , C ( O i ,S ) similar to the Glass curve /Figure. 4.a/.

• b.    When a _i ( S ) < a < a ₂ ( S ) , the shortest length search OKW curve is drawn from the edge circle C ( O i ,S ) from point OK , K to circle C ( O 2 ,S ) . KW ( W E C ( O 2 ,S ) ) consists of the perpendicular. Here, the angles of reflection on K E C ( O i ,S ) of segments OK , KW are the same and equal to e ( S, a ) (Figure. 4.b).

• c.    When 0 < a < a i ( S ) , the curve with the shortest length is segment OK = OA . K = A and A locate the point of intersection of the circles C ( O i , S ) , C ( O 2 , S ) which is closest to the circle C (0 , 1) : A E C ( O i ,S ) П C ( O 2 ,S ) (Figure. 4.c).

  

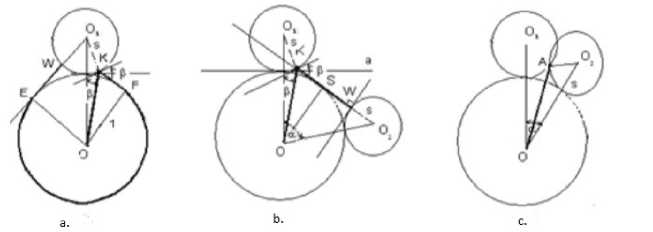
Figure. 4. The shape of the shortest length search curve changes depending on the value of the angle α

Our goal is to find formula for a i ( S ) , a ₂ ( S ) and e ( S, a ) -angles, and the lengths of short search curves. First, find a ₂ ( S ) /Figure. 4.a/ and e ( S ) is the solution of equation (6).

• a = Z O i OK + Z KOS + Z SOO 2 .

S is the point of tangency. So

Z SOO 2 = arccos ^-$; Z KOS = ^П — ( n — 2 e ( S )) = 2 e ( S ) — ^П

^ |OK| =

cos(2 в ( S ) - 2 )

1        _     1

cos( П ) — 2 в ( S )   sin2 в ( S )

According to the cosine formula

S ² = (1 + S ) ² +

1 sin2 в ( S )

2(1 + S ) sin 2 в ( S )

cos Z O 1 OK

and

1 о n         /(2 S + 1)sin ² 2 в ( S ) + 1\

' = ■   . s          .■( s ) ^— 2 ⁺ ■       ^ _{2( S} +Bsin2 e ( S ) J ⁽⁷⁾

But when a 2 ( S ) < a <  2 n , the length of the shortest curve expressed by the formula

• d ( a, S ) =--1— — cot 2 в + p 2 S + S ² — 1            (8)

cos 2 в

Now consider the case a i ( S ) a <  « 2 ( S ) /Figure. 4.b/.

O1 = S, O1O = S + 1, ZOi KO = П + в according to the cosine theorem

( S + 1) ² = S ² + OK ² — 2 S • cos( ^П + в ) = S ² + OK ² + 2 S • sin в.

Considering this quadratic equation for OK

OK = — S • sin в + ^ S ² • sin ² в + 2 S + 1             (9)

Since Z OKO 2 = п — 2 в , if the cosine theorem is applied to the triangle A OKO 2

( S + 1) ² = KO ² + KO 2 — 2 KO • KO 2 cos( n — 2 в ) =

= KO ² + KOI + 2 KO • KO 2 cos(2 в )

This will be a quadratic equation for KO 2 , whose only positive root is completely defined by the formula

KO 2 = — KO • cos 2 в +  ( S + 1) ² — sin ² в • KO ²        (10)

KO is expressed by formula (9). Let’s write the following formula to find the dependence of angle β on parameters α , S .

a = Z O 1 OK + Z KOO 2 = arccos

2 S + 1 + KO ² , 2( S + 1) OK ⁺

+ arccos

KO ² + ( S + 1) ² — KO 2 2 OK ( S + 1)

In deriving this formula, the cosine theorem is applied to the angles Z O 1 OK and Z KOO 2 of triangles A O 1 OK and A KOO 2 , respectively. в ( S, a ) is fully defined by formula (11).

The minimum length of the demand curve is found by the formula.

( a,S ) = OK + KO 2 - S

But in order to find a i ( S ) , we need to use the condition

KO 2 - S = 0

From the formula (13), we will find the formula for the dependence of the angle β on S . And from the formula (11)

2 S + 1 + KO ²        KO ² + 2 S + 1

S ) = arccos 2 OK ( S + 1) ^{+ arccos} 2 OK ( S ₊ ц

As a result of the above analysis, the following theorem is confirmed.

Theorem 2.2. For the policy of detecting and destroying enemy fire points with incomplete information formulated at the beginning of this section, the numbers 0 < a i ( S ) < a 2 ( S ) <  2 n can be found, expressed by formulas (7) and (14).

• a.    When a 2 ( S ) < a <  2 n , the shortest length search curve OKFEW consists of segments OK , KF , EW and arc FE /Figure. 4.a/. The reflection angle e ( S ) is expressed by the formula (6) and the length of the search curve is expressed by the formula (8).

• b.    In case a i ( S ) < a < a 2 ( S ), the search curve with the shortest length consists of two segments: OK , KW and /Figure. 4.b / reflection angle e ( S,a) is (9)-(11) by formulas, and its length is calculated by formula (12).

• c.    0 < a < a i ( S ). In this case, the demand curve with the shortest length will be the segment OK = OA , and its length can be found from the formula.

d ( a, S ) = OK = OA = (1 + S ) cos | -   (1 + S ) cos | - 2 S - 1

Proof. Formulas other than (15) were confirmed in the previous analysis. Now let’s derive formula (15). For this, let’s write the cosine theorem for A AOO 2 .

S ² = ( S + 1) 2 + OA ² - 2 OA ( S + 1) cos |.

Consider this quadratic equation in terms of segment OA

OA 1,2

( s +1) cos — ±

( S + 1) 2 cos ² — — 2 S — 1

there are two roots. Because the sign (+) corresponds to the far intersection point B of circles C ( O i ,S ) ,C ( O 2 ,S ) /Figure. 4.c/ (-) symbol should be selected. The theorem is proved.

Conclusion

• 1.    This study examined the model of enemy positioning, done a complete analysis, formulated and found solutions.

• 2.    This solution is an extension of the search solution by [2] and [3]. The idea of this solution has given rise to many search solution related to practice.

• 3.    The formulation of such a solution will further enrich the military science theoretically, and will be of particular importance.