The simplest formulas of natural selection
Автор: Pavel S. Zamaliev
Журнал: Доклады независимых авторов @dna-izdatelstwo
Рубрика: Biology
Статья в выпуске: 28, 2014 года.
Бесплатный доступ
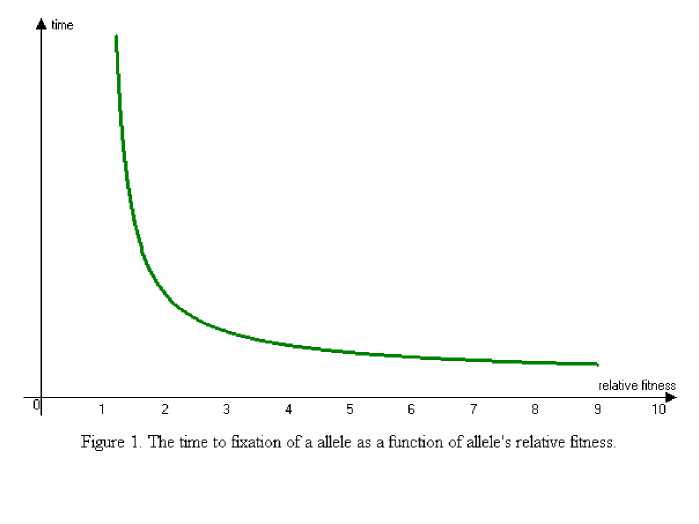
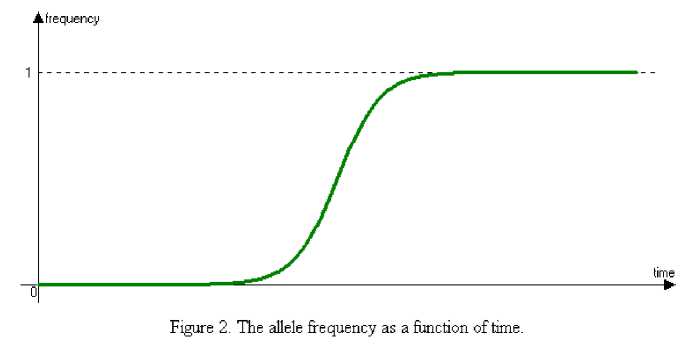
The dependences are found for haploid population: time to fixation of a allele as a function of population size and allele's relative fitness; allele frequency as a function of time; natural selection's speed as a function of time; natural selection's speed as a function of allele frequency
Короткий адрес: https://sciup.org/148311835
IDR: 148311835
Текст научной статьи The simplest formulas of natural selection
The simplest formulas of natural selection
Annotation
The dependences are found for haploid population:
-
• time to fixation of a allele as a function of population size and allele's relative fitness;
-
• allele frequency as a function of time;
-
• natural selection's speed as a function of time;
-
• natural selection's speed as a function of allele frequency.
We can affirm that the beneficial allele's frequency increases regularly. Therefore, time of change of beneficial allele's frequency is a function of some variables. We can write this function for a haploid population.
Let the allele X replaces the allele x in a haploid population. Let the population size is A . Then the ratio of the number of alleles X to the 1
number of alleles x is A at the moment t 1 , when allele X is one only.
A
The ratio of the number of alleles X to the number of alleles x is — — A
1
at the moment t 2 , when allele x is one only. We need to find time to fixation of allele X T — t 2 — t 1 .
Let number of alleles x is a , and number of alleles X is b at a moment t . Let number of alleles x is c , and number of alleles X Is d at the moment t + 1. Then the progeny of one individual with the allele x is at unit time. The progeny of one individual with the allele X is ab at unit time.
cd
The ratio--i--is the relative fitness of allele x. Manifestly ab cd
--i--< 1. We must say that this relative fitness is used in population ab genetics usually. But we will use the relative fitness of allele X. The dc dc relative fitness of allele X is W =--i— . Manifestly--i— > 1 and ba ba d c_(c d V b"a "Ia"bv ■ dc db
So, W =-- i--, hence W =-- i--. ba ca
b is the ratio of the number of alleles X to the number of alleles x
a at a moment t .
d is the ratio of the number of alleles X to the number of alleles x
c at the moment 1 + 1.
Hence w shows how much the ratio of the number of alleles X to the number of alleles x increases at unit time. Hence the ratio of the wn number of alleles X to the number of alleles x is at the moment
A
-
1 1 + n , and the ratio of the number of alleles X to the number of alleles
TT ww x is --- at the moment L = 1 + T . Hence A =---, and
A 21 A
T =
2lnA ln w
The ratio of the number of alleles X to the number of alleles x Is
wt
A at a moment t . Let the frequency of allele X is p at the moment t .
t wt p w
Hence --- =----- , and p =------ -.
A 1 - p A + w
Let the frequency of allele X Is m at a moment 1 1 , and let the frequency of allele X is n at a moment 1 2 ( m < n ) . Hence
ln n (1 - m)
w1 w2 . m (1 - n)
------— — m, ------— — n , and At — t^ — t, = . We see
A + wt1 A + wt2 21 In w that time for which frequency of allele X changes from m to n , isn't function of population size.
Manifestly p is natural selection's speed V :
r
V — p —
wt ln w w2t ln w
1 1 —
A + w t ( A + w t')'
P —
t
w
A + wt
hence V — p ln w — p 2 ln w.
Aspeed
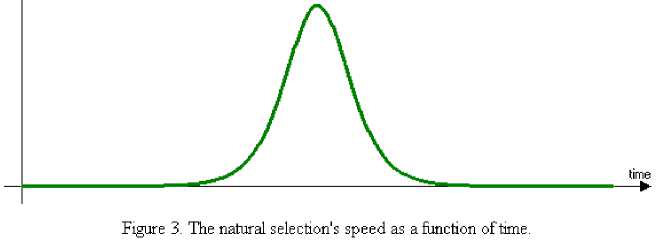
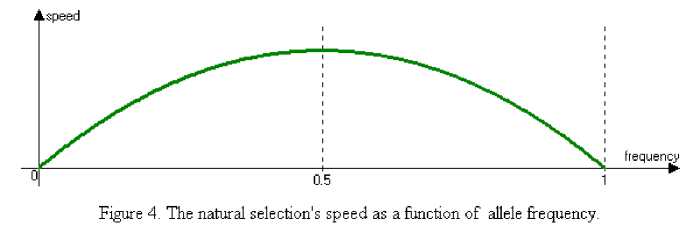
We see that natural selection's speed has a maximum when the frequency is equal to 2 , and natural selection's speed tends to zero when the frequency tends to zero or one. And it is known.


