The Simulation Analysis of Nonlinear for a Power Amplifier with Memory Effects

Nonlinear power amplifiers(PAs) for signals near the saturation region will have a serious spectral regrowth which causes adjacent channel interference and in-band distortion which degrades the bit-error rate(BER) performance. To ensure the efficiency and the correct signal transmitting of PAs at the same time, a PA linearization technique should be adopted. Although the transfer function of PAs is linear, its dynamic characteristics also cause a distortion called linear distortion which is easy to compensate by linear filter. However, the nonlinear distortion is inherent in the active device. The even terms in the polynomial fitting will introduce integer multiples of the frequency components and the nonlinear distortion which is called harmonic distortion, and the odd items will affect the baseband output of system. In the wireless communication system, a strict band-pass filter can filter the harmonic distortion completely; therefore it’s only need to consider the odd items nonlinear distortion of PAs.

Researches on the PA memory effect is the basis of numerical analysis of PA working condition, so many scholars have worked in this area and made a lot of achievements. S. Boumaiza and F.M Ghannouchi established thermal memory effects modeling in PAs, and discussed how to compensate it in predistortion linearizres[1]. Since the number of parameters in general form Volterra series model will increase rapidly with the system order and memory depth growing which results in a large amount of computing of parameter identification, its adhibitions are limited to low-level weak memory nonlinear systems. H. Ku et al. proposed a behavioral model based on the previously developed memory polynomial model [2]. It is actually a simplified form of the Volterra series model, due to the number of parameters which is far less than the number in the same order and memory depth Volterra series model, the computationally intensive of model identification is reduced greatly. In practical applications, the predistortion technology based on Volterra series is difficult to realize the self-adaption and track nonlinear drift of PAs, so predistortion is not ideal [9]. Zhong Pei-lin et al. used a compressing quantization method to design a non-iterative look-up table predistortion method based on waveform training, which effectively improved the power spectrum of the signal and the bit error rate performance of system, and minished the intermodulated power of signal[3]. Lv Xiu Jie et al. studied the realization form of linear subsystem in Hammerstein predistorter and the predistortion structure for identifying the predistorter parameters with the high-efficient lease square algorithm. The Hammerstein predistorter can efficiently compensate the nonlinear distortion of PAs with memory effects[4]. Zhan Peng et al. proposed the single-feedback predistortion method based on memory polynomial, which can avoid the IQ imbalance errors caused by the down-conversion circuit, reduce the costs and improve the linearization performance of digital predistortion[5]. Li Bo et al. presented a novel fractional order memory polynomial predistorter and the corresponding coefficient estimation algorithm[6]. Yang You Fu et al. proposed an open-loop memory polynomial pre-distorter based on look-up table, which can effectively compensate memory nonlinearity distortion of system due to high-power amplifier, and dramatically improve the system BER performance[7]. However, when a lookup table is used to indicate the inverse character of the power amplifier, a more complex and larger one will be required, which makes convergence of the table become very slow. N. Naskas et al. proposed a neural-network-based adaptive baseband predistortion method for RF PAs, which can achieve a significant linearity improvement that reaches 25 dB[8]. Yang Zhao, Zhang Qin, Xia Gaofeng, Liu Jiong proposed a digital predistortion linearization algorithm using multi-stage look-up-table predistorter with optimal linear weighted delay for memory power amplifiers, and the new algorithm achieved better linearization results validated by hardware tests[9]. Hosein Miar-Naimi and Hamid Rahimpour analyzed the effects of phase and gain imbalances between two signal branches in linear amplification with nonlinear components transmitters and presented a new algorithm whose advantages are zero residual error and fast convergence time[10]. Mei Yen Cheong et al. proposed novel direct and indirect learning predistorters (PDs) that employ a new baseband simplicial canonical piecewise linear (SCPWL) function. The performance of the proposed PDs is easily controlled by varying the number of segments of the SCPWL function[11]. Felice Francesco Tafuri, Cataldo Guaragnella, Marco Fiore, and Torben Larsen proposed a linearization by means of a new type of digital predistorter, defined directly in the I-Q domain. The enhancement of this model with additiona I-Q terms can guarantee a more versatile compensation when the distortion comes from the joint contribution of the PA and the quadrature modulator[12]. Oishi, Y. et al. described a method to design a predistorter for a power amplifier with a memory effect by using nonlinear parameters extracted from measured intermodulation distortion for a GaN-FET amplifier. And they confirmed that a fifth-order predistorter was effective up to a higher power level[13]. Farouk Mkadem et al. expounded a complexity-reduced Volterra series model for radio frequency power amplifier(PA) behavioral modeling and digital predistortion(DPD) by analyzing the memory effect mechanisms of the PA[14].

The traditional way to identify predistortion based on adaptive networks is to use a training sequence to extract the PA model. Adjusting the appropriate training signal range can make power range covered by the entire gain characteristic range of PAs, which is from linear amplification to begin to distortion to complete saturation[15]. When the training signal is output to the amplifier, the obtained feedback signal is easily to correspond to the original training sequences synchronously, which greatly simplifies the problem. The synchronization technology’s functional circuit is complex and it also needs to solve the problem of loop delay. Although the adaptive LMS algorithm based on Newton iteration can obtain a high precision solution, while reducing the time complexity, the initial estimation problem of matrix sequences has a great impact on convergence of the algorithm[16]. At first, this paper uses limiting baseband predistortion technology to establish the fitting polynomial of nonlinear Pas and gives memoryless predistorter’s parameters based on objective programming algorithm of matrix analysis. The obtained satisfactory solution of predistorter does not depend on the specific characteristics of the nonlinear. Secondly, this paper researches the BPNN model accuracy of PAs and the relationship between generalization ability and the number of training samples and hidden layer neurons. Also it establishes a tapped delay BPNN model for the distortion characteristics of PAs with memory nonlinearity. Simulation results show that this model fits the nonlinear characteristics of PAs with memory precisely.

This paper is organized as follows. In Section 2 we present the memoryless effect predistortion algorithms and obtain satisfactory solution of predistorter which does not depend on the specific nonlinear characteristics. In Section 3 we establish the nonlinear PA model with memory effects based on BPNN with tapped delay nodes. In the next section we illustrate our simulation and analysis. Section 5 makes a conclusion for this paper.

• II.    The Memoryless Effect Predistortion Algorithms Based On Analysis Of Phase Angle And Amplitude

• A.    The mathematical model of nonlinear PAs

Set as the input signal of PAs, where r > 0n represent the amplitude and phase angle respectively. Then the corresponding output signal amplitude is as follows:

z ( r . ) = G^TRh\x = rn

= h (1) x (t) + h ( 2 ) x (t )3

+ h ( 3 ) x ( t ) 5 + h ( 4 ) x ( t ) 7

where z (rn) n = 1,2,-•-,1000 is the output signal amplitude in simulations , G = [h (1), h (2), h (3), h (4)]T is fitting polynomial coefficient vector of PAs characteristics,  G ( ) is the nonlinear characteristic function of PAs , and R = [x (t), x (t)3, x (t)5, x (t)7 J is the orthogonal basis vectors.

The output signal AM and PM of PAs are mainly determined by the amplitude of the input signal and almost independent of the phase of the input signal[17]. So the memoryless PA will only produce amplitude-to-amplitude modulation (AM-AM) distortion. To avoid Runge phenomenon, we use seven times polynomials, and polynomial contains only odd items.

• B.    Predistorter goal programming model based on matrix analysis

  1000                                 ₂

Set J ( f , ) = X G • ( f ,)„ R * l , " 8<-|        (2)

n = 1

Where F ⁽ x ⁽ t ) ) = ( ^f₈\ R * is the characteristic function of a predistorter, which produces the corrective action in the opposite direction for the nonlinear compensate of PAs and is fitted by polynomial matrix, and constant g is the ideal amplitude magnification of PAs. The total effect makes the overall input-output characteristic linearized, and the output power be fully utilized.

(NMSE) can be described by

N

XIz (n)-z(n )l

NMSE = 101g - nn^--------

XI z ( n )|2

n = 1                                   (3)

For the minimum value of NMSE, as well as the best linearization degree of PAs, we obtain equations as follows:

J , = 0

5 f ,          i , j = 1,2,--.,4

,

Using Mathametica 7.0.0 to solve (4), we obtain the following equations:

f f ,1 )

^f2 ^f .3

V ^f .4 у

a 10 a 11

a 20 a 21

a 30 a 31

a 40 a 41

a 1,12

a 2,12 a 3,12

a 4,12 _

( 1 f 21-   2 24 f ,1- f 34 f .Г" -f 44 ) "

In order to give full play to the role of PAs, making the average output power maximize must be considered in building the predistortion processing model. This paper establishes an objective programming model which consists of NMSE, maximizing power limiting output amplitude,

and other constraints

after

determining the nonlinear characteristics of PAs.

Set     f 21 ,    , f 24 , f 31 ,    , f 34 , f 41 ,    , f 44

decision variables of the objective programming.

min Z = p_xd + + pd ₂

<

NMSE + d f- d + = c P + d ₂" - d + = c^ |x ij -|^ M , i , j = ^1,•••^,4 d - , d ; >  0, l = 1,2

as

the

Since the oversized input amplitude will cause an overflow saturation of PAs, it’s need to limit the predistortion output amplitude to not be greater than the maximum of the given input amplitude of PAs. In (6), the bigger the signal average power after predistortion

N

processing P =

N

N Xk f j L R *

¹ ' n = 1

is, the

x = x ( n )

n = 1

better[19]. According to the average output power of PAs, the average input power target can be calculated. P 1 = з , P 2 = з , 16 rigid constraints meet | x ( n )| <  M .

The tolerance M of input amplitude is determined by the maximum amplitude of the input signals, i.e., M is the maximum module value of elements in the matrix

( f j ) .

^{F (} x ( , n ) ) = C f j),., = 1„..,₄ ^R*V . n = 1,2,™, N

• III.    The Nonlinear Pa Model With Memory Effects Based On Bpnn With Tapped Delay Nodes

A basic BPNN is composed of the input output layer which consists of input output nodes and tapped nodes, and the hidden layer which consists of hidden layer nodes. The larger the size of the network is, the stronger capability of network function mapping is, the stronger the memory of the training samples is, while the worse the fault tolerance of a new sample is ,as well as, the worse the generalization capability of the network is[18].

x - min (x) max (x)- min (x)

where x is the input signal amplitude of, x _ n is the input signal amplitude after normalization, min ( x ) is the minimum value of the input signal amplitude, max ( x ) is the maximum value of the input signal amplitude.

In the BPNN model, the input node is the input amplitude of PAs, and the output node is the output amplitude and output phase angle of PAs.

If BPNN needs to reflect the memory characteristics of PAs, it must add a delay link at the input node, i.e., add tapped delay nodes, and the number of nodes is the memory depth m of PAs. By Matlab simulation analysis, the BPNN fitting effect becomes more and more ideal with tapped delay nodes increasing, but the algorithm running time is getting longer and longer, and work efficiency is lower and lower. Taken together, the best number of tapped nodes in this model is 3.

In BPNN, if the numbers of hidden layer nodes are different, fitting results obtained are also different. When the number of hidden layer nodes is 6, the fitting curve can reflect the original PA nonlinear characteristics well. The different excitation functions will also affect the fitting effect of neural network model. Frequently-used excitation functions are logsig, pureline, poslin and tanhsig[20]. In this paper, we use sigmoid excitation function which can reflect the nonlinear characteristic of PAs well. Nonlinear model for a single input - dual output neural network model and contain six single hidden layer nodes.

The solving steps of BPNN model are as follows:

n sj Z^a   oj, i=1

bj-f (sj)=^ • j = 1,2,---, p

@ Calculate the input { L_t }

of each unit of the output

layer, and calculate the response {C_t } of each unit of the hidden layer by Sigmoid function.

p

Lt = Z ^v t^bj ^- Y t ^,

= 1

C = f (Lt )= 1 + e" Lt ’ t = 1,2,---, q

@ Use    {C_t }    and

hope output

samples

Yk = (yx,•••,yn) to calculate the generalization error {dk} of each unit of the output layer, and correct connection weights {v^z} and thresholds {y } by {bj}.

dk =(Yk -C)C(1 -C), k = 1,--,m

Vj, (N +1) = v, (N) + Pd^bj

Yj (N +1) = Yj (N) + pd^,  i = 1,--, n

V " ^} by ^{{ o} j } .

q

ek = Zd Y) bj (1 — j • j = 1.2.

V t = 1     7

, p ,

jN + 1) = ®j ( N) + веХ           (12)

6j(N +1) = Oj(N) + pPj. i = 1,.--,n

® Randomly reselect a learning mode pair from the n learning mode pairs, and return to © until the BPNN global error function E is smaller than a preset value, i.e., the network converges. E is calculated by (13);

( y k - C ) 2

mmq

E = Z Ek =ZZ k=1          к=1 t=1

• IV.    Simulation Analyse

  Running the Matlab procedure, we obtain Fig. 1 and Fig. 2. While fitting (1), we obtain vector G = [3.0279, -0.6683, -1.4093, 0.9523f and Fig.3. So the amplitude polynomial of PAs is following:

G ( x ) = 3.0279 x -0.6683 x ³

-1.4093x 5 + 0.9523 x ⁷

Fig. 1. Memoryless PA input / output phase angle scatter

Fig. 2. Memoryless PA input amplitude / output phase angle scatter

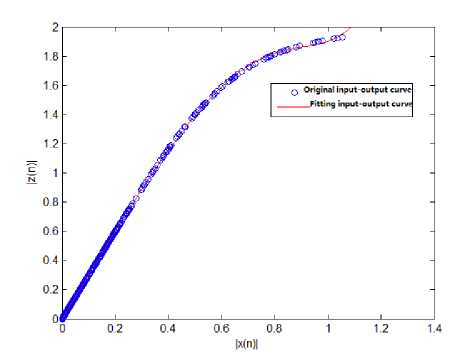
Fig. 3. Memoryless PA input /output polynomial fitting

Table 1. Memoryless predistorter simulation results

Matrix ( f j )				M	NMSE	P
0.7241	0.0649	0.0743	0.0743
0.2000	0.3000	0.2000	0.2000	1.1168	-10.2629	0.1851
0.3000	0.2000	0.2000	0.200
0.2000	0.3000	0.2000	0.200
0.7241	0.0743	0.0184	0.0743
0.2000	0.2000	0.3000	0.2000	1.1301	-10.2628	0.1808
0.3000	0.2000	0.1000	0.2000
0.2000	0.2000	0.3000	0.2000
0.6776	0.0523	0.0743	0.0523
0.2000	0.1000	0.2000	0.1000	0.9993	-10.2640	0.1606
0.2000	0.2000	0.2000	0.2000
0.2000	0.2000	0.2000	0.2000
0.6310	0.1058	0.0523	0.0057
0.2000	0.2000	0.1000	0.1000	0.8817	-10.2623	0.1435
0.1000	0.2000	0.2000	0.1000
0.2000	0.1000	0.2000	0.2000
0.7241	0.1279	0.0208	0.0988
0.2000	0.3000	0.1000	0.1000	1.2505	-10.2627	0.1809
0.300	0.200	0.200	0.300
0.200	0.100	0.300	0.200

Using objective programming, calling Matlab procedure, then we calculate the corresponding M, NMSE and P . In table 1, the best group is P = 0.1851, NMSE= -10.2629.

Using BPNN to solve nonlinear model of PAs with memory, we obtain results in Fig. 4.

As shown in Fig 1, the red fitting curve is almost covered by the original input data, i.e., BPNN output results reflect the nonlinear characteristic of PAs effectively. Since the established neural network model is single input and dual output, i.e., the original output signal is divided into amplitude and phase, the evaluation of this model should be divided into two parts. In this model, amplitude normalized mean squared error ANMSE = -17.135; phase normalized mean squared PNMSE = -13.324; so we can conclude that the model can well fit the nonlinear characteristics of PAs with memory.

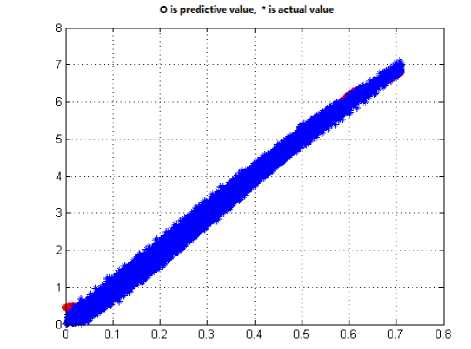
Fig. 4. BPNN output amplitude

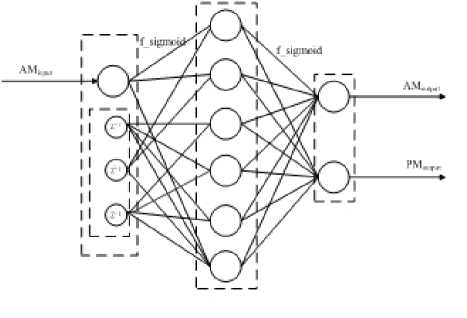
Fig. 5. BPNN model

• V.    Conclusion

  In this brief, a memoryless nonlinear PA predistortion model has been presented which can consider the efficiency nonlinear characteristics of PAs reasonably. Simulation results show that when the maximum average output power of the predistorter reaches 0.1851, the normalized mean square error is only -10.2629. In addition, a predistortion scheme of memory BPNN with tapped delay nodes has been proposed, which can eliminate the in-band distortion results from the memory nonlinear PA. In future work, we will consider the predistorter model with memory PAs, which can not only improve efficiency of PAs, but also reduce spectral regrowth.

Acknowledgment

I would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments.

This work was supported in part by the Innovation Program of Shanghai Municipal Education Commission (Grant No.12ZZ185), Natural Science Foundation of China (Grant No.61075115), Foundation of No.XKCZ1212.