The stress-strain state of a rectangular covering spatial truss

The problems of designing and calculating large-span structures have always been relevant in engineering practice. The idea of unsupported overlap of large areas comes from the works of F. Brunelleschi on the dome of the Cattedrale di Santa Maria del Fiore in Florence (XV century), the project of a 298-meter single-arch bridge across the Neva by I. Kulibin (XVIII century), the Manege truss in Moscow by the engineer A. Betancourt (XIX century), and others. Calculation of the strength and stability of such structures has always been carried out numerically using mathematical models of the structure with varying degrees of approximation. If for a long time the main method for calculating structures was numerical calculations [1-5], then with the advent of symbolic mathematics systems [6], it became possible to calculate structures in analytical form with obtaining calculation formulas suitable both for a simple assessment of the strength and deformability of structures, and for accurate calculation of their performance, regardless of the number of constituent elements. Analytical formulas are especially effective in those cases when they are designed for a wide class of structures. The width of the construct class is determined by the number of independent parameters in the formula. For regular trusses, this is, for example, the number of elements in the periodicity of the structure - panels or groups of panels. The base model for almost any design is a statically definable schema. To the conclusion of analytical dependencies of statically definable trusses of the regular type, we apply the induction method, tested on the solution of problems on the deflection of arches [7-10], lattice [11-13] and spatial trusses [14]. In [15,16], algorithms for deriving exact analytical formulas for regular systems without the use of computer mathematics systems are presented.

Probably, the problem of finding statically definable regular trusses was first raised by Hutchinson R. G., Fleck N.A. [17,18]. Some problems of periodic rod structures are discussed in [19].

In this work, based on the spatial coverage model, we propose a symmetrical square coverage with supports on its lateral sides (Fig. 1). The task is to derive a formula for the deflection of the structure and analyze the forces in the rods.

2    Methods

Truss construction . Having a rectangular size 2 na x 2 nb in plan, the truss on the sides rests on vertical rods. Together with two horizontal mutually perpendicular bar-type ties, the support A is a spherical joint. Support B is a cylindrical hinge (Fig. 2).

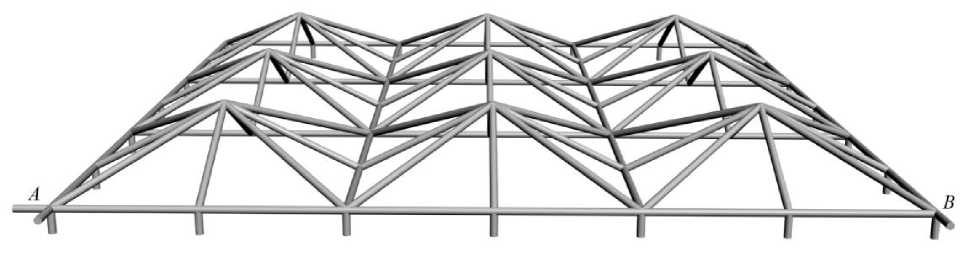
Fig. 1. Truss, n = 3

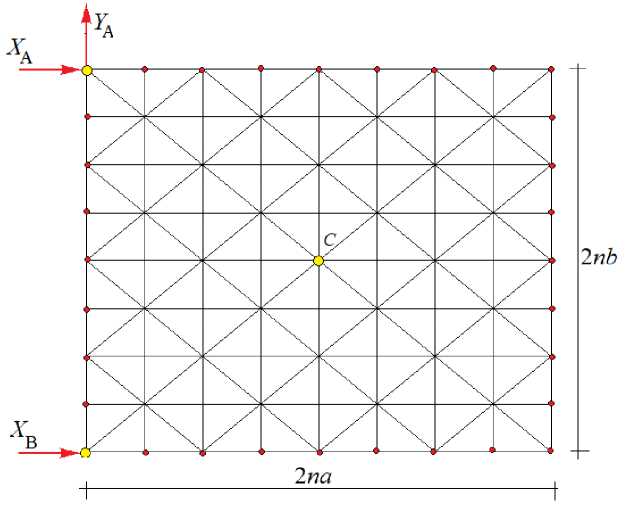
Fig. 2. Truss, n =4, view from above

Together with the rigid members that simulate the supports, the truss contains ns = 12n2 +12n + 3 members. Each pyramidal truss panel with height h consists of eight horizontal rods of length a and b and eight inclined rods connected at the top of the pyramid. All connections in the truss are hinged. The truss is statically determinate — the number of internal hinges m = 4n2 + 4n +1 is three times less than the number of unknown forces in the rods. However, the reactions of the supports cannot be determined from the equilibrium condition of the entire structure as a whole. The truss is outwardly statically indeterminate. This means that the reactions of the supports must be among the unknown systems of equilibrium equations for all nodes of the truss. With the goal of obtaining an analytical solution, we will compose this system using a program written in the system of computer mathematics [20].

The coordinates of the hinges are entered into the program. First, the coverage is assumed to be planar:

x_k = ( i - 1) a , y_k = ( j - 1) b , z_k = 0, k = i + ( j - 1)(2 n + 1), i , j = 1,...,2 n + 1.

A non-flat surface is given by the coordinates of the hinges along the z -axis:

Z k = f ( i , j ), k = i + (2 n + 1)( j - 1),    i , j = 1,...,2 n + 1.

In the considered construction, the heights of the pyramids alternate:

f ( i , j ) = h (1 + ( - 1) ‘ )(1 + ( - 1) j )/4. Other variants of the surface shape are also possible (Fig. 3, 4).

Fig. 3. f ( i , j ) = hi ² j ²

Fig. 4.   f ( i , j ) = h ( j ² + j )

There is a limitation on the shape of the surface. The surface should not contain nodes connecting the elements lying in the same plane, since in this case, the equation of the node's equilibrium on the normal to the plane will not hold. The problem of choosing and analyzing such surfaces of structures' coatings was considered in [21-25]. The detailed monograph [26] on this topic should be mentioned separately.

Calculation of forces. The system of equilibrium equations for the nodes is compiled in matrix form. The matrix G of coefficients, which are the direction cosines of the forces, is written in a cycle by the number of nodes. In the lines numbered 3 j – 2, j = 1, ..., m , the cosines of the angles between the forces and the x -axis are entered, in the lines numbered 3 j – 1 — the cosines of the angles with the y -axis, and in the lines numbered 3 j – the angles with the vertical the z- axis. Direction cosines are calculated from the coordinates of the ends of the elements and the data on the mesh structure written in special vectors containing the numbers of the ends of the elements. The system of equilibrium equations has the form GS = Ф , where S is the vector of forces in the elements and reactions of supports, Φ is the vector of load. The number of support elements located on the sides of the truss and at corners A and B is 8 n + 3. The length of the force vector (the number of unknowns in the problem) is n . The vector Φ is filled with loads according to the same principle as the matrix by the direction cosines. Vector elements Φ are split into triplets, one for each node. In the first element of the triple, the projection on the x -axis of the external load applied to this node, to the second and third – the projection of the load on the y and z axes.

Consider the case of a vertical load distributed over all nodes of the coverage: ФМ_2=ФМЧ= 0, Ф3£ = P, k = 1,...,(2n +1)2. The distribution of forces over the rods obtained from the solution of the system GS = Ф is given in Figure 5. The solution in the Maple system using the matrix inversion operator has an extremely simple form: S = Ф / G. Stretched elements are highlighted in red, compressed elements are highlighted in blue. The black elements are unloaded. The thickness of the lines is proportional to the moduli of the forces in the corresponding elements. Also signed are the values of some forces related to the value of the load P applied to each node of the truss.

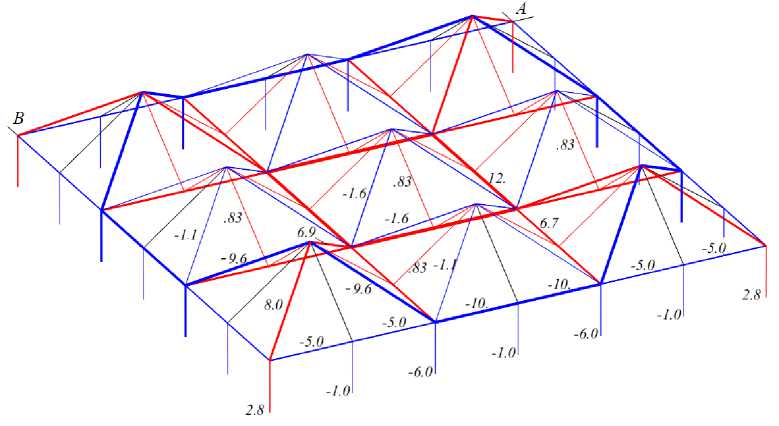
Fig. 5. Relative forces in the rods and support reactions from the action of the distributed load, n =3, a = b = 4m, h = 3m

The calculation shows that all the elements along the lower outer contour of the truss are compressed, and the elements inside the lower chord are stretched. The reactions of all support elements, except for corner ones, are directed upwards (the elements are compressed). Using the induction method, you can get the dependence of the force in any truss element on the number of panels.

Let us give, for example, formulas for support reactions. Due to the symmetry of the structure and load, for a truss with n panels along each side, it is sufficient to obtain formulas for the Z_x,Z ₂,..., Z„₊₁ reactions (Fig. 6). Performing the calculation of forces in symbolic form (the values of dimensions and loads are not specified), we obtain a sequence of reaction values for different values of the number of panels (Fig. 7). Obviously, reactions with even numbers are always equal to the load: Z_{Ik n} = P , k = 1,..., n , and reactions with odd numbers (except for angular ones) are calculated using a simple formula Z i,„ = 2 nP , k = 1,..., n - 1. . To determine the formula for angular reactions, it is necessary to calculate in analytical form the forces in several trusses with a sequentially increasing number of panels.

We have the following sequence of coefficients: -5/4, -1/4, 11/4, 31/4, 59/4, 95/4 ... To determine the general term of this sequence, we find the recurrent equation that it satisfies. Using the operator rgf_findrecur of the Maple system, we obtain the linear homogeneous equation

Z 1,_п = 3 Z 1,_п - 1 - 3 Z 1,_п - ₂ + Z 1,_п - 3 .

The solution to this equation is given by the operator rsolve . Thus, we have the following dependence: Z „ = Z ₂„_+1Я= P (4 n ² - 8 n - 1)/4. Note that the resulting formula does not include the dimensions of the structure and only for n = 1 and n = 2 the reaction of the angular support is directed upward (the force in the rod is less than zero), in all the rest In some cases, this support does not support the covering, but keeps it from shifting upwards.

Fig. 6. Truss, n = 4, side view. Support reaction symbols

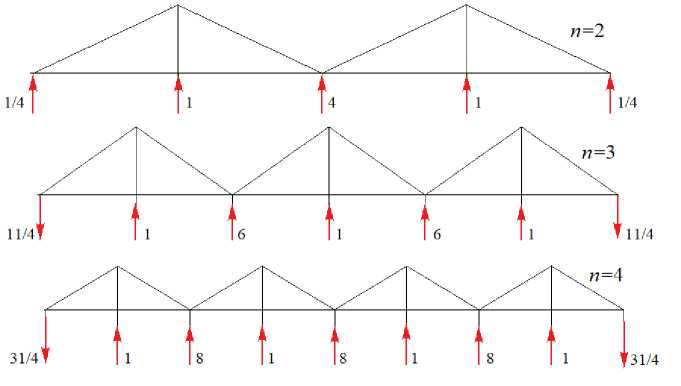
Fig. 7. Relative reactions of supports, n = 2, 3, 4

Concentrated load. The used calculation algorithm has the advantage that it can be easily reprogrammed for any load. To do this, it is enough to change the vector Φ . Consider the load by one vertical force at the central point of the coverage C . The vector Φ has only one nonzero element Ф_м_₂ =Ф_ЗИ = 0, Ф_; = P , k = 1,...,(2 n + 1)². The reactions of the supports, in this case, turned out to be quite simple, for their determination the induction method is not required. Nonzero reactions are in the corners of the structure Z_x „ = У. _1И=- P /4 and the middle of the sides: Z_n„ = P (1 - ( - 1) ⁿ )/8 ,

Z n + 1, n = P (1 + ( - 1) ⁿ )/4 .

The calculation of the deflection equal to the vertical displacement of the node C (Fig. 2) is performed according to the Maxwell-Mohr's formula n,-8n-3

A = P £ j=1

( S j )² l j EF ’

where l and S are the length and force in the j -th rod from the action of a vertical unit force applied to the central node C, E is the elastic modulus of the rods, F is the sectional area. It is assumed that the stiffness of the bars is the same. The amount does not include 8 n + 3 forces of non-deformable support rods. The sequential calculation of the deflection of trusses with n = 1,2,3 ... panels gives a series of formulas of the form

A = P ( C ( a ³ + b ³) + Cc ³ ) / ( h ² EF ) , (2)

where is the brace length, and the coefficients form the sequences

C = 1/64, 3/32, 17/64, 15/16, 81/64, 105/32... , C = 1/64, 1/16, 5/64, 1/4, 17/64, 9/16,...

The common members of these sequences are obtained in the same way as the support reactions using Maple operators

C = ((5 + ( - 1) ⁿ ) n ³ - (5 + ( - 1) ⁿ ) n - 3( - 1) ⁿ + 3) / 24, C = (( - 1) ⁿn + n ² - n + 1 - ( - 1) ⁿ )/4.

3    Results and Discussion

Formula (2) with coefficients (3), obtained for the deflection of the pavement under the action of a concentrated load on it, can be illustrated by graphs, from which some features of the solution become clear. Let us introduce the value of the dimensionless deflection A ' = A EF / ( PL ), where L is denoted as the length of the side of a covering that is square in plan a = b = L / (2 n ) . The curves of the graphs attract attention primarily by the fact that they have a pronounced non-monotonic character (Fig. 8). For low heights of the structure, the jumps in the deflection values at a change in the number of panels by only one reach 30%. The reason for this non-monotonicity is probably that, depending on the evenness of the Kirsanov, M.

The Stress-Strain State of a Rectangular Covering Spatial Truss;

number of panels, the middle of the covering (point C ) falls either on the top of the dome ( n is odd) or on the node in the lower chord of the truss ( n is even).

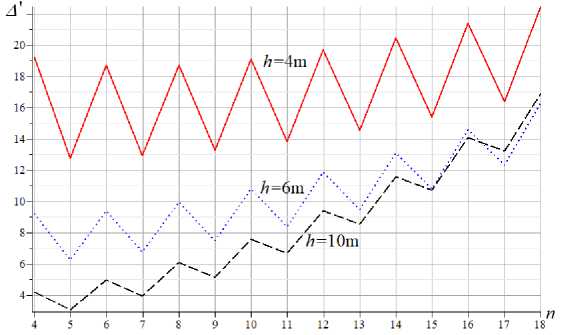
Fig. 8. Dependence of the deflection on the number of panels, L = 2 na = 60 m

It is also worth paying attention to the effect of the self-intersection of curves plotted for different heights at n = 15. This follows from the nonlinearity of the result and means that trusses with the same number of panels, but different heights, can have the same deflection. In general, despite significant jumps, the deflection with an increase in the number of panels on average increases. Moreover, using Maple, you can even find a nonlinear (quadratic) asymptotic dependence:

lim A 'Z n ² = h I (4 L ) . n ^^

The dependence of the deflection on the height of the truss is also nonlinear (Fig. 9). At the beginning of the graph, at low altitudes, the curves behave quite predictably: with increasing altitude, the deflection decreases. However, an increase in the deflection is also noticeable after certain values of heights, which gives reason to believe the existence of some optimal rigidity height of the truss. The increase in deflection is not evident for all panel numbers. For example, for n = 10, the curve goes down all the time. However, if we take the height limit of dependence (2), then it turns out that these curves have a linear asymptote with a positive slope lim A 'I h = ((1 - (-1)n )(1 - n) + n 2)Z(4 L), which, in the h ^x presence of a decreasing section at the beginning of the graph, guarantees the existence of an extremum. The only disappointing factor is that the values of the heights corresponding to the extremes are too high.

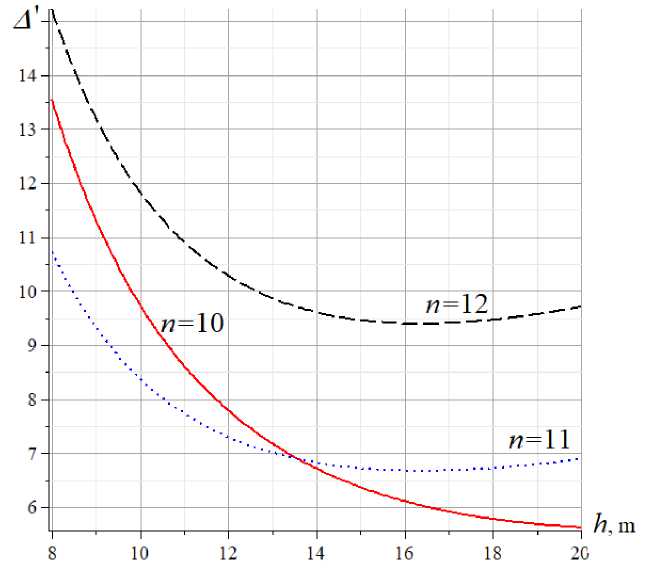
Fig. 9. Dependence of the deflection on the height, L = 2 na = 40 m

Formula (2) for the deflection is derived in the case of a concentrated load. We have not yet succeeded in repeating the same result for a distributed load. An analytical solution is obtained by running Maple in the symbolic mode, which is significantly slower than the numerical mode. Since the common term by the Maple methods can be obtained from a sequence of sufficiently large length, to achieve the result it is necessary to calculate the deflection of a large number of trusses with a sequentially increasing number of panels. The number of rods in a spatial truss of the considered type depends on the square n, and the number of elements of the matrix of the system of equilibrium equations is proportional to the square of its order. Therefore, the counting time has a dependence on the number of panels of the fourthorder. To fix the counting time, the Maple system has a time () operator. Its work, of course, depends on the speed of the processor. So, on the Intel CORE i7 processor, the calculation of the deflection at n = 1 takes 0.047 s, at n = 2 — 1.06 s, n = 3 — 6.65 s, n = 4 — 27.75 s, n = 5 — 94.65 s. The calculation of the deflection with n = 12 took hours and did not make it possible to single out the common term of the sequence, since the sequence of length 12 does not allow finding the pattern of formation of its elements. It is necessary to continue the calculation with more panels. However, even the simplest extrapolation of time expenditures based on work experience [7-14,20] shows that it may take a year or more to get the result. Therefore, at the moment, only a numerical method remains to solve the problem for a distributed load. In this case, the results can be obtained in the same program that gave formulas for the concentrated load in symbolic form, switching it to numerical calculation and correcting the vector Φ of the right side of the system. The corresponding solution curves are qualitatively close to the curves in Figures 8 and 9. These curves also have a jump-like shape, self-intersection points, a non-monotonic increase in deflection with an increase in the number of panels. There are also extreme points on the curves of deflection versus truss height.

Calculation and design of long-span coatings [26,27], including surfaces made of brick or masonry [22, 23] and synthetic sun-reflective coatings [24], has always been one of the priorities of engineers, designers and mathematicians. This, of course, is primarily determined by the practical necessity of such structures in the construction of hangars, gyms and facilities. In addition, well-designed structures always have a special architectural expressiveness [26]. Mathematicians, however, large-span coatings modeled by surfaces of the most bizarre shapes are attracted by the opportunity to apply accumulated, often very abstract scientific developments in practice. In the present work, to the set of problems on this topic, the problem of finding analytical solutions is added, which are attractive because they can be applied without loss of accuracy to the calculation of structures with a large or very large number of elements. The peculiarity of three-dimensional problems is manifested primarily in a multiple increase in complexity compared to solving problems with flat trusses [7-13]. In the calculated pavement structure, it was not possible to obtain an analytical solution for the case of a uniform load. Earlier, the same difficulty associated with the time resource was found in the analysis of such coverage in [14]. This is not to say that the situation here is hopeless. One way out is to use Maple's ability to work with many cores simultaneously (parallelizing the counting process). Another way out is to obtain analytical formulas for the dependence of the forces in individual elements, similar to what was demonstrated above when calculating the reactions of supports, with the subsequent inclusion of these solutions in the Maxwell -Mohr's formula. This requires the development of an appropriate algorithm, which is a separate task.

4    Conclusions

The peculiarity of the proposed scheme of spatial coverage is that it is a statically definable truss with a real location and number of supports. In the standard case, a spatial truss should have six supports, while on the plane there can be no more than three support points, which forces us to resort to solving the simplest problem of the force method, which boils down to selecting statically permissible loads, one of which simulates a support. This complicates the solution in case the loads are asymmetrical, uneven, or lateral. Here, due to the choice of the mesh-like shape of the coating surface, consisting of separate rod pyramids, it was possible to symmetrically place the supports on the sides of the coating. The applied algorithm for composing the equilibrium equations made it possible, in the case of a force concentrated in the center of the pavement, to obtain a formula for the dependence of the deflection not only on the load and dimensions of the truss, but also on the number of panels. The formulas are in the form of cubic polynomials with variable sign coefficients. The analytical form of the solution made it possible to single out the quadratic asymptotics of the deflection in terms of the number of panels and linear in height. In the case of a distributed load, the solution was obtained in symbolic form only for individual efforts, in particular, for support reactions. It was found that with such a design scheme, the corner supports do not support the coating, but have downward reactions. It is noted that the applied induction method for obtaining solutions in symbolic form in some cases has a significant limitation on the resource of the solution time.