The theory of real options in the estimation of consecutive innovative projects

On novelty level two types of innovations are distinguished – radical (basic) and improving innovations. Radical innovations are aimed at adoption of new generations of machines and materials, essentially new technics and technology, they make such considerable changes in processes, products or services that lead to transformation of the existing markets or sectors or create the new markets and sectors. Improving innovations are aimed at evolutionary improvement of the properties and parametres of processes, products or services, they serve a purpose of distribution and perfection of the mastered generations of technics and technology, creation of new models of machines and variety of materials, improvement of parametres of the produced goods, services and their manufacturing techniques [1]. Distinctive feature of the majority of innovative projects is constant improvement of an innovative product (improving innovations), that allows to mark out certain generations of development of technology. In many projects the innovative product of one generation is considered as a platform (base) for the future generation of innovative products. The approach is offered to the estimation of innovative projects the outlet of which is limited (the demand is set by certain limits which is typical for a number of innovative sectors) and where the competition exists. The competition is the important factor as it is the competition that forces the manufacturer to launch constantly innovative products.

Let us assume there is a company which plans to launch innovative products P_t = 1,…, T through equal time intervals t , where T is the life-time of the technology. Each of the subsequent products P_{t + 1} is the improvement of the previous product P_t and after the beginning of manufacturing of a new generation product P_{t + 1} manufacturing of a previous generation product P_t ceases. Initialinvestmentexpensesforlaunchingofeachproduct P_t make up I_{t –1}, and the net cash flow from selling of one product makes up C_t . One of the major factors of uncertainty for the company is the demand for the product in each period ( x_t ) and it is known that the demand under good conditions makes up x_t+ and x_t– under bad conditions. In the first period the probability of high demand is q ₁ and the probability of the low demand is (1 – q ₁). For the subsequent periods the following is valid:

– if the demand for the product P_t was high, the probability of the high demand for the product P_{t + 1} makes up q_t+ , and with the probability (1 – q_t+ ) itwillbelow.

– if the demand for the product P_t was low, the probability of the high demand for the product P_{t + 1} makes up q_t– and with probability (1 – q_t– ) it will be low.

On the basis of the information above it is possible to draw the following decision-tree of the cash flows (fig. 1).

Fig. 1. Decision-tree of cash flows for consecutive innovative projects

According to the NPV method for estimation of the appropriateness of the project realization it is necessary to determine cash flows for each period considering the probabilities, i. e. expected cash flow of the period 2:

f 2 = q 1 ■ ( q 2 ■ ( c 2 ■ x 2 - I 2 ) ^{+ (1} - q 2 ) ■ ⁽ c 2 ■ x 2 - I 2 )) ⁺

^{+ (1} - q 1 ) ■ ⁽ q 2 ■ ⁽ c 2 ■ x 2 - I 2 ) ^{+ (1} - q 2 ) ■ ⁽ c 2 ■ x 2 - I 2 ))- ⁽¹⁾

After that each of the expected cash flows should be discounted to the initial time period at the discount rate k (where k is set from the outside, as expected rate of return from alternative investments). Formula of NPV looks as follows:

NPV =

T t=0

f t

(1 + k ) '

new product, switching over to different technologies etc. [2; 3; 4] Strategic net present value of the project (NPV *) consists of two summands:

• –    net present value of the project without options (NPV);

• –    value of options of the project (ROV).

The formula for the strategic (expanded) net present value looks as follows:

NPV*=NPV+ROV.         (3)

Let us consider the opportunity of the abandonment of the project by the example of the decision-tree in figure 1. The decision-tree should be analysed from the end. It makes sense to abandon the project, if discounted cash flows are less than investment expenses:

The project is accepted ifNPV >  0 and is rejected ifNPV < 0.

At the same time the main disadvantage of NPV method is that it does not consider the possibility of management of the project to make changes during its implementation, for example, to expand or reduce production capacity, to temporarily shut down the project with the subsequent renewal of activity, to abandon the project etc. Implementation of these measures influences NPV positively and reduces the risk of the project. For the projects implying constant renewal management decisions may include the measures of the choice of the best period of time to launch a

I t -i

q, ■ x , ⁺ +^{(1 -} q t ) ■ x - i + k

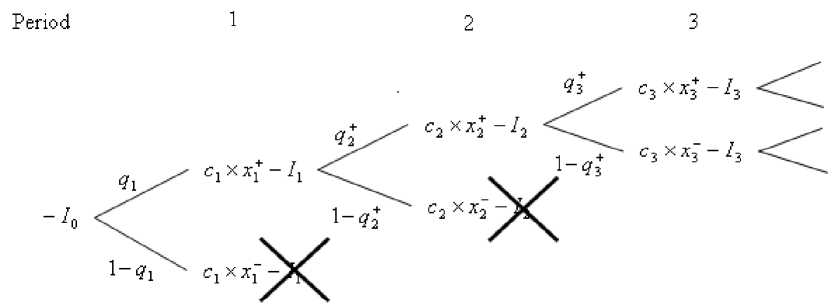
The given check should be carried out in each node of the decision-tree, moving from right to left from the end of the tree (period T ) to its beginning. In each node it is necessary to sum up the cash flows of the period and the future cash flows discounted to this period. The decision-tree of cash flows is transformed to a following decision-tree of value (fig. 2).

Asaresultofthecarriedoutanalysiseconomicallyinefficient branches of a tree will be cut downwhich leads to the modified tree of cash flows, for example, as following (fig. 3).

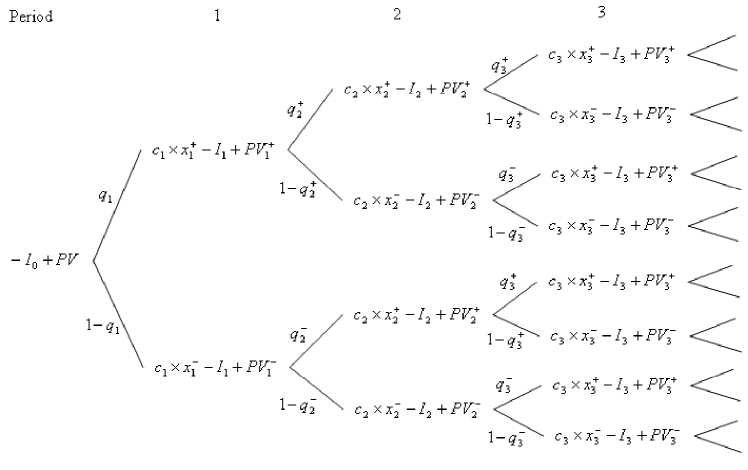
Fig. 2. Decision-tree of value for consecutive innovative projects

According to the method of decision tree analysis (DTA) for the modified decision-tree of cash flows the expected cash flows are calculated and then are discounted to the initial moment of time at the rate k. That is:

T

NPV  =y f* ,

DTA    * ^ 0 (1 + k ) * ,                   (5)

where NPV DTA >  NPV

A shortcoming of the decision-tree analysis (DTA) is that it does not provide any instructions on modifying the discount rate of the project in connection with the risk reduction through exclusion of the unfavorable branches. To solve this problem it is possible to use real options approach (ROA) which allows not only to take into account the flexibility of management decisions but also to correct the discount rate according to the theory of financial options [3; 4].

Let us consider the following numerical example. The company plans to launch two consecutive products P ₁ and P ₂. Investment expenses for launching the product P ₁ make up 1,000 c. u., those for launching the product P ₂ make up 2,000 c.u. The cash flows of product P ₁ will make up 700 c.u. at favorable demand, 300 c. u. at unfavorable demand, for product P ₂ they will make up 5,500 c.u. and 2,000 c. u. accordingly. The probability of favorable demand for product P ₁ is50%, ofunfavorabledemand100%–50%=50%. The probability of demand for product P ₂ depends on demand for product P₁ . If the demand for product P ₁ was high the probability of a high demand for product P ₂ makes up 80 % (theprobabilityoflowdemandis100%–80%=20%). If demand for product P ₁ was low the probability of a high demand for product P ₂ makes up 30 % (probability of low demand is 100%–30%=70%). Thediscountrateofthe projects of the given branch of industry ( k ) makes up 30 %, riskfree rate ( r ) makes up 10 %. It is possible to present a decisiontree of cash flows of the project in a following way (fig. 4).

Period 0                12

ол^550

05 X 4300

(700 - 2000) oX"-- WOO

-WOO <'

X           0 35500

0,5X"

- 1700 <; -....

(300 — 2000) o,7 WOO

Fig. 4. Decision-tree of cash flows for the company

Estimating the project with the NPV criterion it is possible to come to a conclusion that the project is inefficient:

NPV = - 1000 + O_;5.( _Z 13OO) _± 0_;5.( _Z 17OO) ±

1 ± O.3

O.5_:(O.8 _: 55OO ± O.2 _: 1OOO)±O.5_:(O.3_:55O0±O.7 _: 1OOO) = 98 (6)

±                           (1 ± O.3)²                           ~     .

To take into account the abandonment option we will build the following decision-tree of value (fig. 5).

Analyzing a decision-tree of value it is possible to make a conclusion that in case of the low demand for the product P ₁ investment in the product P ₂ is inefficient as the net present value of such project is negative (NPV₁ ^- = –I ₁ +PV₁ ^- =–2000 +

+ 1808 = –192 c. u.). The modified decision-tree of cash flows taking into account the abandonment option at low demand for the product P ₁ will look as follows (fig. 6).

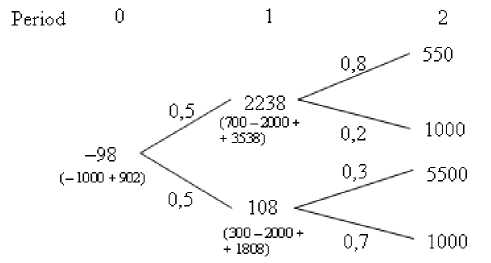
Fig. 5. Decision-tree of cash flows for the company

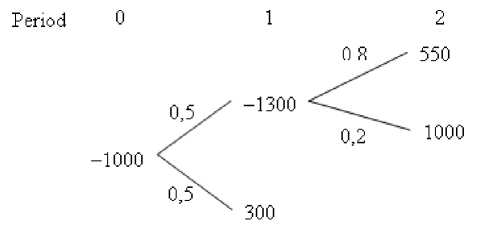
Fig. 6. Modified decision-tree of cash flows for the company

The net present value according to the decision-tree analysis (DTA) is then worth:

^NPV DTA ⁼

1 _OOO| O.5 . ( - 1,3OO) + O.5 . 3OO ₊

^,                    1 + O.3

O.5 ■ (O.8 ■ 5.5OO + O.2 - 1, OOO)

±            (1 + O.3)²

= - 24 c. u.

The value of the option is worth:

ROVDTA=–24–(–98) =74c. u.

At the same time despite of the fact that the risk of the project has been lowered due to the reduction of dispersion of the cash flows, the discount rate remained invariable. To modify the discount rate it is necessary to take advantage of the theory of real options and risk-neutral approach. The risk-neutral approach assumes the determination of the riskneutral probabilities for the cash flows of the project for the purpose of discounting the additional value of the project appearing as a result of management flexibility at the riskfree rate (as this value does not imply an additional risk). From figure 5 it follows that the present value of cash flows inperiod t =0makesup902 ( S = 902), which is obtained by weighing the value of the project in period t = 1 by the actual probabilities in case of favorable ( S ⁺=2,238) andunfavorable ( S ^- = 108) scenarios and discounting the result at the interest rateof30%.

The risk-neutral probabilities can be found as follows:

1 + r - d p= —(Г, u - d

where u = S⁺/S, d = S^–/S.

Intheexample(fig. 7) u =2238/902=2.48; d =108/902 = =0.119; p =(1+0.1–0.119)/(2.48–0.119) =0.415or41.5 % (fig. 8).

The abandonment value of the project will look as shown in figure 9.

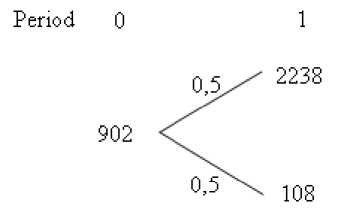
Fig. 7. Present value of the project using the actual probabilities

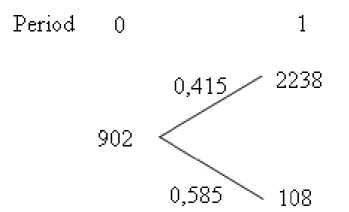
Fig. 8. Present value of the project using risk-neutral probabilities

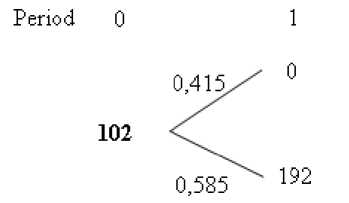
Fig. 9. The value of the abandonment option

Thus, NPVROA=NPV+ROVROA=–98+102=4c. u.

Comparison of results of an estimation of consecutive innovative projects is presented in table.

The classical assessment criterion of the investment projects (NPV) indicates that the project is economically inefficient. At the same time the abandonment option is built into the project of launching the product P₂ inthecaseofthe low demand for the product P ₁. There are two ways of the estimation of the existing opportunity to terminate the project (the real option to abandon): a method of the decision-tree analysis and the method of real options analysis. The method of DTA underestimates the option value as it does not consider change of the project risk. The cash flows of the projects are discounted at the cost of capital of the project k = 30 %. The present value of the option in this case makes up 74 c. u., and expanded NPV is – 24c. u. Themethodofreal options considers reduction of risk of the project by using the risk-neutral probabilities and discounting the cash flows at the risk-free rate r = 10 %. Defined according to the method of real options the value of the option to abandon makes up 102 c. u. This leads to the fact that the strategic net present value of the project becomes positive (NPV = 4 c. u.), therefore the project can be recommended for implementation.