The Use of ANFIS and RBF to Model and Predict the Inhibitory Concentration Values Determined by MTT Assay on Cancer Cell Lines

Published Online April 2016 in MECS

• I . Introduction

  Lung cancer is leading cause of cancer-related deaths among cancer patients [1], with an estimated of 1.61 million new cases and 1.38 million deaths worldwide in 2008 [2]. Lung cancer has two main types, non-small cell lung cancer (NSCLC) and small cell lung cancer (SCLC). NSCLC accounts for approximately 85% of all lung cancer cases and making it a major global public health concern [1]. Doxorubicin (DOX, trade name Adriamycin) is a naturally occurring anthracycline antibiotic [3]. DOX has been in use since the late 1960s and is a widely used anti-cancer agent in chemotherapy [4].

DOX, alone, or in combination, is an important drug in the treatment of the lung cancer and other cancers, but bone marrow and cardio-toxic effects of DOX limit its use in clinical medicine [5]. Therefore, there is a need to explore the adjuvants and/or natural compounds that can effectively reduce the doxorubicin-induced toxicity to improve its chemotherapeutic efficacy [6]. A number of adjuvants and natural compounds have been tested to increase DOX chemo-efficiency [5]. Chrysin is one of them. Chrysin (5,7-dihydroxyflavone) is a naturally occurring flavonoid that is widely distributed in medicinal herbs [5] and has displayed numerous chemopreventive properties against the chemically induced toxicities.

Chrysin has also shown to have the anti-growth properties against the various cancers in animal models and in the different human cancer cell lines like human colorectal cell line and prostate cancer cell line [6,7]. Recently reported study by Brechbuhl et al. [8], showed that Chrysin induces cancer cell death synergistically in combination with DOX [6,8]. In the study of Brechbuhl et al. [8], MTT [3-(4,5-dimethylthiazol-2-yl)-2-,-5-diphenyltetrazolium bromide] assay has been conducted to measure the cytotoxicities (IC 50 values) of the combination drug therapy with Chrysin and DOX against the cancer cell lines. The MTT colorimetric assay is one of the most widely used assays for estimating the cytotoxicity, viability of animal or bacterial cells and proliferation studies in the cell biology [9, 10].

This method has been widely used to screen for the cytotoxic compounds during the development of chemotherapy or to screen for the unwanted cytotoxic effects during the preclinical studies [10].

By considering the substantial failure rate of adjuvants and/or drug candidates in the late stage development and the expensive and time consuming process of measuring toxic effects, the predictive tools that can eliminate inappropriate compounds seems necessary [11] and can play significant role in providing the missing data of cytotoxicity of new adjuvants and/or drug candidates.

In the recent decades, new methods such as artificial neural networks (ANNs) and adaptive neuro-fuzzy inference system (ANFIS) have been used to develop the predictive models to estimate the needed parameters. Computational intelligence (CI) techniques are now being used as an alternative to the statistical tools [12-15].

In this paper, the applicability of ANFIS and radial basis function (RBF) network, which is a type of ANNs, for prediction of IC 50 values evaluated by MTT assay in human cancer cell lines are investigated. For this purpose, we are used the experimental data reported in Brechbuhl et al. [8] for developing the proposed models.

The prediction capability of the proposed ANFIS and RBF models can be used to fill the gaps of data for untested concentrations and their IC 50 values of new adjuvants and/or drug candidates for cancer drug screening. These models can be used to predict the unknown data by saving time and money.

• II.    Experimental Data

For developing the proposed ANFIS and RBF models, we used the experimental data. To obtain the experimental data, the IC 50 of combination drug therapy with Chrysin and DOX has been determined against the cell lines by the MTT assay.

Briefly, the lung non-small cell epithelial cancer (NSCLC) cell lines A549, H157, H460 and H1975 have been cultured at 37°C with 5% CO 2 . The NSCLC cell lines have been grown in the media and supplements and then have been seeded in 96-well plates.

After indicated treatments, 20 µl/well of MTT solution has been added and incubated for 3-4 h, then 150 µl/well of DMSO has been added to dissolve formazan crystals. The absorbance of each well has been observed by a plate reader at a test wavelength of 570 nm. The IC50 values have been calculated using prism version 5. For more details of the assay conditions and the experimental data, the readers are advised to refer to the work of Brechbuhl et al. [8].

• III.    Modeling Using RBF

In the mathematical modeling a radial basis function (RBF) network, is an ANN, which uses RBFs as the activation functions. Its output is a linear combination of RBFs of the inputs and the parameters of neurons. RBF networks have many applications such as function approximation, prediction of time series, and system control.

The RBF has a feed forward ANN structure consists of three layers (one input layer, one hidden layer and one output layer) as shown in Fig.1. [16, 17]. The input layer is made up of the source nodes that connect the network to its environment.

The second layer consists of a set basis function units that carry out a nonlinear transformation from the input space to the hidden space [18]. The output from jth neuron of the hidden layer is given by:

(

Z,= K

II - -dII

I ^{o 2} j J

j = 1,2,..., k

where k is the number of neurons in the hidden layer, o j is the width of the receptive field in the input space from unit j, K is a strictly positive radially symmetric function (kernel) with a unique maximum at its center ( ц , ), which drops off rapidly to zero away from the center. This implies that Z_j has an appreciable value only when the distance || — - ц , | is smaller than the width o j [19]. Given an input vector X , the output of the m ^th neuron in the output layer is given by:

У т ( x ) Aw ™ ?, ( x ) m = 1,2,..., M (2) j = 1

where w_jm is the weighting factor. The training process of the RBF networks can be typically done by a two-step algorithm. The center vectors of the RBF functions in the hidden layer are chosen randomly from some set of examples in the first step.

Also, these center vectors can be determined by k-means clustering. In the second step, a linear model is fitted to the hidden layer's outputs using the least squares function.

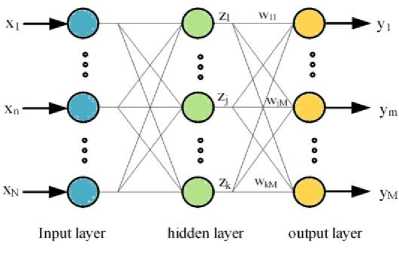
Fig.1. RBF structure.

The RBF network is a strong tool for prediction and simulation in engineering applications. In this study, the RBF model is developed for prediction of the inhibitory concentration values assessed by the MTT assay on human lung epithelial cancer cell lines co-treated with Chrysin and doxorubicin. The inputs of the proposed RBF model are the concentrations and the types of the cell lines and the output is the IC50 value in the A549, H157, H460 and H1975 cell lines. The data set required for training the proposed RBF model is obtained using the experimental values [8]. To build the RBF model, the experimental data are divided into two sets. The number of the samples for training and testing are chosen 21 (75%) and 7 (25%), respectively. For training the proposed RBF model, a computer program is developed using MATLAB 7.0.4 software. The best proposed RBF network being used in this study is obtained with 21 neurons in the hidden layer.

• IV. Modeling Using ANFIS

  An adaptive neuro-fuzzy inference system (ANFIS) is a kind of artificial neural network (ANN) that is based on Takagi-Sugeno fuzzy inference system (FIS). ANFIS is a universal estimator. ANFIS was developed in order to integrate the benefits of both ANNs and FISs in a single framework to approximate nonlinear functions. ANFIS is a multilayer feed-forward network, which combines the advantages of both ANN (e.g., learning capacities, optimization capacities, and connectionist structures) and FIS (e.g., human like “IF-THEN” rules, thinking and ease of incorporating expert knowledge) to map an input space to an output space [20, 21]. In this study, the prediction of the inhibitory concentration values assessed by the MTT assay on the human lung epithelial cancer cell lines cotreated with Chrysin and doxorubicin using ANFIS is presented. The proposed ANFIS model is shown in Fig.2., where the inputs are the concentrations and the types of the cell lines and the output is IC 50 value in the A549, H157, H460 and H1975 cell lines.

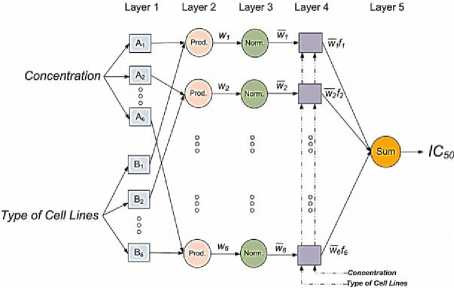
Fig.2. The proposed ANFIS model.

A description of the layers in the proposed ANFIS model is defined as follows [22, 23]:

Layer 1. Each node in this layer is an adjustable node, marked by the square node. The node functions of this layer are given by:

A i (Con ) = ц _А1 ( Con ), i = 1,2,...,6             (3)

B i ( TCL ) = ц вi ( TCL ), i = 1,2,...,6            (4)

where Con (concentration) and TCL (type of cell lines) are the inputs of the model and μ (Con) and μ (TCL) are the fuzzy membership functions. In this study the membership function is Gaussian membership function and is given by:

0.5⁽ x a )

G ( x ) = Exp (-------)                 (5)

^bi ²

Parameters in this layer are referred to as premise parameters (nonlinear parameters). As the values of these parameters change, the Gaussian function varies accordingly.

Layer 2. Each node in this layer is an adjustable node, marked by the circle node. The output of this layer is given by:

W i = A ( Con ) X B i (TCL ), i = 1,2,...,6          (6)

Layer 3. Each node in this layer is a fixed node, marked by the circle node. This layer estimates the ratio of the i ^th rule’s firing strengths to the sum of all rule’s firing strengths as follows:

W i = W^— ,   i = 1,2,...,6                  (7)

• 2    W j j = 1

Layer 4. Each node in this layer is an adjustable node, marked by the square node. The output of this layer is given by:

f_t = W i ( m i Con + n i TCL + k i )  , i = 1,2,...,6         (8)

Where mi, ni and k  are called the consequent parameters (linear parameters).

Layer 5. Each node in this layer is a fixed node, marked by the circle node. The output of this layer is given by:

ic 50 = :2 f- (9) i = 1

The aim of the ANFIS training is to tune all the parameters (the consequence and premise parameters) to make the ANFIS output match the training data. ANFIS uses the Hybrid learning algorithm, which is a two-step process. In the first step (the forward direction), the consequent parameters are identified by the least square estimation and using the gradient descent the premise parameters are updated. In the second step (the backward direction), the premise parameters are updated by the feedbacked error values. When all the values of the parameters are changed, the membership functions are also modified. The data set required for training the proposed ANFIS network is obtained using the experimental values. For developing the ANFIS model, the experimental data are divided into two sets. The number of samples for training and testing are 21 (75%) and 7 (25%), respectively. In this study, different ANFIS structures are tested and optimized to obtain the best ANFIS configuration. By testing the various ANFIS structures with the different number of membership functions, we obtained the optimal structure with 6 membership functions for each input. Also, we tested all types of the membership functions like Bell, Sigmoid, Triangle, Trapezoid and Gaussian. The Gaussian membership function in comparison with the others had the better results. Table 1. shows the specification of the best proposed ANFIS model.

Table 1. Specification of the proposed ANFIS model.

Type	Sugeno
Inputs/outputs	2/1
No. of input membership functions	6 for each input
No. of output membership functions	6
Input membership function type	Gaussian
Output membership function type	linear
No. of fuzzy rules	6
No. of nonlinear parameters	48
No. of linear parameters	24
No. of epochs	150

RMSE =

CF = 1 -

N

Z ( X i ( Exp ) - X i (Pr ed )) 2

i = 1

N

Z ( X i ( Exp ) - X i (Pr ed )) 2

i =1 _______________________________________

N

Z ( X i (Exp )) 2

i = 1

V. Results and Discussions

In this section, the proposed RBF and ANFIS models for the prediction of the IC 50 values are compared with each other and with the experimental data. The training and testing results for the proposed RBF and ANFIS models in comparison with the experimental data are shown in Table 2., Table 3., Fig.3. and Fig.4., where the mean relative error percentage (MRE %), the mean absolute error (MAE), the root mean square error (RMSE), and the correlation factor (CF) are calculated by the following equations:

N

MRE % = 100 x — Z   i ( p ) --------)         (10)

N i = 1       Xj ( Exp )

N

MAE = — Z X ( Exp ) - X i (Pr ed )|

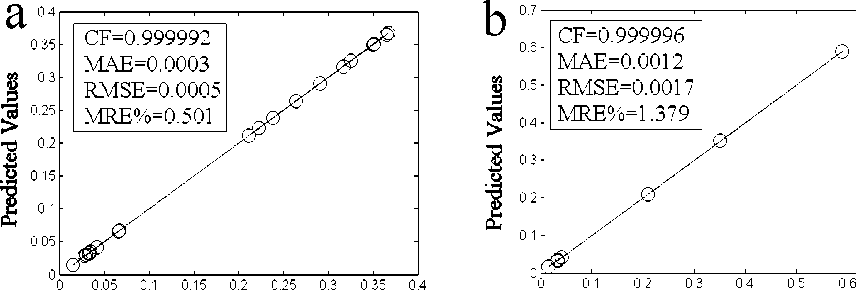
where ‘ X(Exp) ’ and ‘ X ( Pred) ’ stand for the experimental and predicted (RBF or ANFIS) values, respectively and N is the number of data. Table 2. shows the comparison between the experimental and predicted (RBF and ANFIS) results for training data. While in Table 3. the comparison between the experimental and predicted (RBF and ANFIS) results for testing data is shown. As it can be seen in Table 2. and Table 3., there is a remarkable agreement between the experimental and predicted values using both proposed ANFIS and RBF models, which show that the proposed ANFIS and RBF models can be used as the accurate and reliable tools to predict the IC₅₀ values. From Table 2., Table 3., Fig.3. and Fig.4. it is clear that both ANFIS and RBF models have good agreement with the experimental, also the proposed ANFIS model is more accurate than the proposed RBF model. The ANFIS model could significantly reduce the overall (training and testing) MRE% to less than 0.95% in comparison with the RBF model, which has the overall (training and testing) MRE% less than 4.5%. Also, the ANFIS model has a number of epochs 150, which is needed to reach the convergence. In comparison with the proposed RBF model, the time needed for the training the ANFIS model was less than the required time to design the proposed RBF model.

Table 2. Comparison between the experimental and predicted (RBF and ANFIS) results for training data.

Type of cell lines	Chrysin (µM)	IC 50
		Experimental	RBF	ANFIS
A549	0	0.365	0.3542	0.3651
A549	5	0.291	0.2632	0.2907
A549	10	0.264	0.2446	0.2645
A549	20	0.212	0.1933	0.2121
A549	25	0.223	0.2213	0.2228
A549	30	0.238	0.2397	0.2376
H157	5	0.367	0.3485	0.3671
H157	10	0.35	0.3595	0.3520
H157	15	0.317	0.314	0.3169
H157	25	0.325	0.3199	0.3248
H157	30	0.351	0.3523	0.3519
H460	0	0.067	0.0669	0.0670
H460	10	0.035	0.0358	0.0350
H460	15	0.03	0.0285	0.0298
H460	20	0.033	0.0329	0.0329
H460	30	0.015	0.0167	0.0148
H1975	0	0.066	0.0649	0.0660
H1975	5	0.042	0.0438	0.0418
H1975	15	0.028	0.0275	0.0287
H1975	20	0.034	0.035	0.0330
H1975	30	0.035	0.0337	0.0346

Table 3. Comparison between the experimental and predicted (RBF and ANFIS) results for testing data.

Type of cell lines	Chrysin (µM)	IC 50
		Experimental	RBF	ANFIS
A549	15	0.21	0.2294	0.2059
H157	0	0.589	0.5652	0.5878
H157	20	0.351	0.3413	0.3525
H460	5	0.033	0.0347	0.0335
H460	25	0.016	0.0173	0.0162
H1975	10	0.042	0.0435	0.0416
H1975	25	0.034	0.0321	0.0350

Experimental Values                           Experimental Values

Fig.3. Comparison of the proposed ANFIS model with the experimental for (a):training data and (b):testing data.

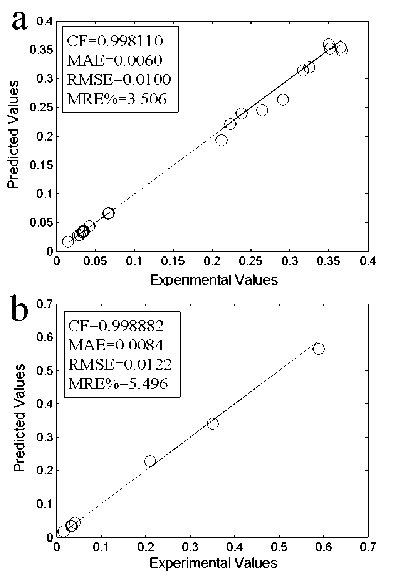
Fig.4. Comparison of the proposed RBF model with the experimental for (a):training data and (b):testing data.

In Fig.5. and Fig.6. the obtained results for IC 50 using the proposed ANFIS model (solid line) and the experimental (circle mark) versus concentration of Chrysin (in the range of 0 µM to 30 µM) for the various type of cell lines (A549, H157, H460 and H1975) are shown. Both predicted values and experimental data indicate that by increasing the Chrysin from 0 to 30 uM (for the type of cell lines A549), the IC 50 sharply decreases, while with further increasing the Chrysin, the IC 50 increases. In this case, the minimum IC 50 (0.213) is happened in Chrysin=16.5 µM. For the cell lines type H157, by increasing the Chrysin from 0 to 30 uM the IC₅₀ sharply decreases at first, while further increasing the Chrysin has no significant effect on the IC₅₀. In this case, the minimum IC 50 (0.32) is happened in Chrysin=15 µM. For all types of cell lines, the maximum IC 50 occurs at Chrysin=0. From Fig.5. and Fig.6. the maximum IC 50 (0.5878) was happened in Chrysin=0 µM for type of cell lines H157. Also the minimum IC₅₀ (0.0140) was happened in Chrysin=28 µM a for type of cell lines H460. From these results it is clear that the proposed RBF and ANFIS models can be used as the accurate models for prediction of the inhibitory concentration values accessed via the MTT assay on human lung epithelial cancer cell lines co-treated with Chrysin and doxorubicin.

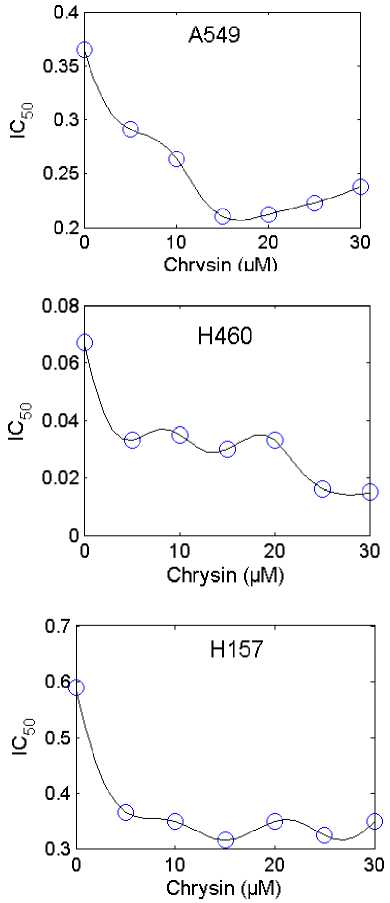
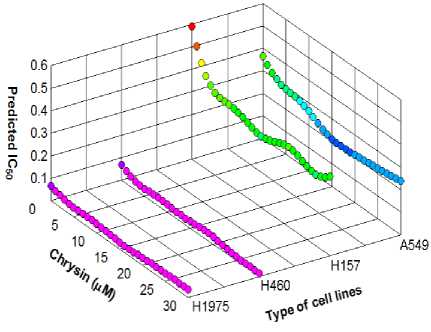
Fig.6. The obtained IC 50 using the proposed ANFIS model as a function of Chrysin in A549, H157, H460 and H1975 cells.

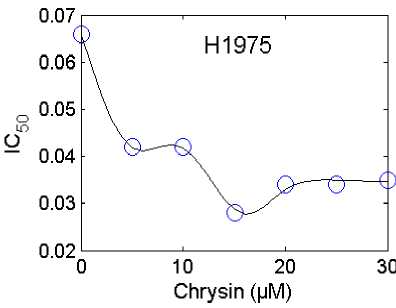
Fig.5. Comparison between the experimental (circle mark) and predicted results using the proposed ANFIS model (solid line) for the types of cell lines A549, H157, H460 and H1975.

• VI. Conclusions

The purpose of this study was to examine the applicability of the RBF and ANFIS models for prediction of the IC50 values evaluated by the MTT assay in the human lung cancer cell lines. The comparison showed that these models are efficient tools for filling the gaps of data for untested concentrations and their IC50 values of new adjuvants and/or drug candidates with saving time and money. The results of the present study can be shown as follow:

• (a)    Comparison of the predicted (The RBF and ANFIS models) and experimentally evaluated IC₅₀ values shows that there is a good agreement between them.

• (b)    The proposed ANFIS model is more accurate than the proposed RBF model.

Therefore, the RBF and ANFIS models can be used as the fast and cheap tools for prediction of the IC 50 values with an acceptable accuracy in situations, where the urgency and/or lack of money prevent a thorough cytotoxicity assay like MTT from being conducted.