The value of initial abstraction and estimation of run-off-forming rainfall rate at a specific geographical location
Автор: Movlud A.Teymurov
Журнал: Science, Education and Innovations in the Context of Modern Problems @imcra
Статья в выпуске: 1-2 vol.6, 2023 года.
Бесплатный доступ
The changes of precipitation and temperature under different scenarios influence on the humidity condition of the territory (HCT) by various effect types. Therefore, when assessing the rate of runoff formation process, water resources and natural risks, is considered a key factor the HCT. At present, there is the tendention in world hydrology science the HCT is estimated mainly on the basis of 3 parameters ─ maximum retention (S), initial abstraction (Ia ) and antecedent moisture condition (AMC). S─is the potential maximum moisture retention of the territory in a concrete physico-geographical condition, Ia ─is the fraction of the precipitation (P) on the moistening of various surface types and other losses before runoff begins, AMC-reflects the previous humidity condition of territory at the moment rainfall beginning and 3 AMC rates are determined (avarage, dry, saturated). In accordance with the runoff formation conditions, the southern slope of the Greater Caucasus are divided into 11 humidity zones. For each of the zones considering 3 AMCs, it’s possible to estimate water resources, runoff generation level and losses, S, Ia and other water balance components for both the multi-annual term and the specific period. The calculations may be realized easily both by the analysis of multispectral satellite images of the territory using rational method, and by the relationships S=f(P) and Ia=f(S) offered by us. The research results are obtained by processing of complex runoff-forming factors using GIS technology, there are high accuracy and their application is possible in solution the major water-related issues.
Rainfall-runoff processes, maximum retention, initial abstraction, antecedent moisture condition, multi-spectral analysis, risk assessment
Короткий адрес: https://sciup.org/16010255
IDR: 16010255
Текст научной статьи The value of initial abstraction and estimation of run-off-forming rainfall rate at a specific geographical location
The provision of safe and reliable supplies for drinking water plays an important role in each country for conservation of existing ecosystems, ecological balance, food safety and security. Today it’s impossible to find such a socio-economic project that its implementation would be realizable without taking into account of water resources. The global climate changes, especially in the context of decreasing precipitation, creates a negative role in the formation of runoff in individual areas, as well as a significant impact on the variability of water resources. The formation of runoff, i.e. the generation condition of surface runoff after rainfall has always been the main theme of hydrology science. Because the level of surface runoff formation, their losses and the amount of water storage for reservoirs has a significant impact on the capacity of the any terrain water resources. As a result, this manifests itself also in increasing of the scientific articles on these field studies. The scientific works devoted to investigation of rainfall-runoff processes and variability of water balance elements have been expanded, in recent years. Modern scientific approaches related to water issues require not only a continuous study, at the same time, in parallel challenges the estimation with a new, modified and sensitive to the natural and human changes methods.
Problem definition, used method and materials
The mechanism of the runoff formation is simply not limited only by the processes of surface runoff generation after the beginning of rainfall. The surface runoff value is such a parameter, so that its calculation plays an auxiliary role in determining of other elements of water balance and soil moisture. Thus, in the US and the most Western countries, during the assessment of water resources and water balance are preferred such methods as it is possible to study the rainfall-runoff model, first of all (Bernard 1938; Chow 1988; Dooge 1977; Fetter 2009).
During long-term investigations and monitoring carried out with SCS (the US Soil Conservation Service) over small river basins with the purpose of studying the situation of the runoff surface formation, in parallel, is studied the actual and maximum water capacity issues too. The changes of precipitation and temperature scenarios may be impact on the area humidity by different scale. The process of runoff generation and volume of water resources is directly related to area humidity condition. Therefore, during the assessment of natural risks and water resources prediction first of all the humidity conditions of the area should be considered (Mohamed E., 2015).
The popularity of the rational method is its convenience, simplicity, predictable, a long history of researches, to pass the modification development ethape, reliable genesis and other factors. The rational runoff coefficient (c) is an parameter used in hydrology for predicting direct runoff from rainfall excess and to assess the level of surface runoff-forming after rainfall. The rational runoff coefficients are parameteres depending on the soil granular structure, LULC (Landuse & Land cover) and slope degrees, etc. The rational method equation is expressed as follow:
Q=kxciA (1)
Where, Q-surface runoff discharge, in m3/sec.; i-the rainfall, in mm.; c-rational (surface) runoff coefficient; A-The drainage area, in km2; k-transition coefficient for convertating the surface runoff discharge by unit m3/sec. (k=0.0000314)
The rational method was used only to measure the peak discharge (for small river catchment, urban hydrology, etc.) at first. Gradually, the method was modified and started in the US with the purpose of assessing infiltration and measuring soil moisture condition together with Curve number method (Thompson. David B. 2006; Yaeger M.A 2009; Sirak Tekleab, Stefan Uhlenbrook, Hubert H.G. Savenije, Yasir Mohamed & Jochen Wenninger 2015;
The US NRCS (SCS) and USDA using in the context the mechanism of surface runoff formation, prepared projects for calculating soil infiltration capacity, its moisture rate and degradation level. The results obtained from experimental and research works with capabilities of this method were collected and published in separate handbooks and manuals, for different watersheds, urban and rural areas (French, R., Pilgrim, D. H., and Laurenson, B. E. 1974; Hawkins, R 2010; United States Department of Agriculture 1986; Rallison R.E et al.).
Simultaneously with the traditional elements of the water balance, in the scientific literature of Western countries, from the point of view of studying the formation of runoff, some values are widely used, which have hardly been used in post-Soviet countries, including Azerbaijan. The most important of these values are the maximum soil retention, the initial abstraction, actual soil retention and the antecedent moisture condition (Mohamed, E. S and Belal, 2015; Kent, Kenneth M. 1966; Ponce V.M. 2015).
evaporation and transpiration, detention and depression storage, ınterception on the plant canopy, soil moistening, etc. before runoff begins.
The study of the relationship between S and Ia plays an important role in determining the interrelation of rainfallrunoff. The ratio Ia=λS shows the level formation of precipitation to runoff in different natural and climatic conditions (4,41,52).
λ-is initial abstraction coefficient and changed inversely proportional to the ratio of humidity condition of territory. The ratio of initial abstraction (I a ) to maximum potential retention (S) was assumed in its original development to be equal to
I a =0.2S (Aron, G., Miller, A. C., and Lakatos, D. F. 1977).
The precipitation in this case turns to a surface runoff, its value was high than the initial abstraction (P˃Ia), ie, only within the conditions of S≥5P a surface runoff can not be formed. The initial abstraction ratio is the most ambiguous assumption and requires considerable refinement at different geographical conditions. If in ordinary normal moisturing cases Ia=0.2S, in dry areas (arid and sub-arid) is assumed Ia=0.3S, but in wet territories is accepted I a =0.1S.
-
3) Actual soil moisture (F )-is factual soil retention after rainfall in concrete geografhical location, it’s in the form F=P-Q-I a (Baltas, E.A.,et al, 2007)
-
4) Antecedent Moisture Condition (AMC)-is the preceding relative moisture of the territory (pervious surfaces) prior to the rainfall event. The territories to the ratio of the humidity state are divided into 3 AMC (1,6,10,13,18, 24,25,38,43, 44,46,47).
-
a) AMC II (average, normal)-shows the average level of the soil moisture and is usually taken I a =0.2S to determine its status. According to available data AMC II is being transferred to other 2 conditions.
-
b) AMC I (dry)-is measured by soil conditions Ia=0.3S.
-
c) AMC III (wet, saturated)-is accepted as Ia=0.1S, but in the extreme humidity condition as Ia=0.05S.
There are different classifications for determinaton of the AMC conditions. In the SCS classification showed an appropriate AMC level based on a 5-day antecedent rainfall (33). (table 1).
Table 1
Rainfall groups for Antecedent Soil Moisture Conditions (AMC)
|
AMC |
Humidity condition |
5-day antecedent rainfall, mm |
|
|
Dry/Dormant season |
Wet/Growing season |
||
|
June-October |
November-May |
||
|
AMC I |
Dry |
Less than 35 mm |
Less than 12 mm |
|
AMC II |
Average |
35-53 mm |
12-28 mm |
|
AMC III |
Saturated |
More than 53 mm |
More than 28 mm |
Thus, when AMC is defined, usually the precipitation falling for the last 5 days is considered the main criterion. If the precipitation is 35-53 mm within the antecedent 5 days before the next rainfall, this is considered normal soil moisture condition (AMC II). For antecedent 5 days the precipitation is less than 35 mm is accepted as AMC I (dry) condition, but more than 53 mm as AMC III (wetting).
It was given for a longer antecedant period (total 15-day previous rainfall and evaporation rates) and more larger areas for another AMC classification (24,42,44,47) (table 2).
Table 2
Seasonal rainfall limits for AMC based on coefficient humidity
|
AMC |
Total 15-day antecedent rainfall, mm |
|||
|
High evapotranspiration September) |
(May- |
Low evapotranspiration (October-April) |
Coefficient humidity |
|
|
AMC I |
< 50 |
< 10 |
< 0.5 |
|
|
AMC II |
50-100 |
10-30 |
0.5-2.0 |
|
|
AMC III |
> 100 |
> 30 |
>2 |
|
To determine the maximum retention within 3 AMC conditions from the transition of the normal moisture state (S2) to the dry (S1) and wet (S2) the following equations are used (45).
I a (I)= 2.281 I a (II) (r2=0.999 ) (5) I a (III) = 0.427 I a (II) (r2=0.994) (6)
The quantitative estimation of those 4 values (S, Ia, F and AMC) has a very important role to address a number of the following issues in the science of hydrology:
-
1) Estimation and prediction of direct surface runoff-forming rate after rainfall.
-
2) Verification of concentration opportunities of surface runoff over catchment and its efficiency for design and construction of water reservoirs.
-
3) Determination of permeability rate and soil moisture condition regardless of spatio-temporal variations.
-
4) Estimation of actual soil moisture and maximum soil retention after precipitation.
-
5) The amount of water consumed for infiltration and the fraction of underground feeding of rivers.
-
6) The forecasting for more efficient land use.
-
7) Determination of the water resources and water balance elements.
-
8) Assessment of soil water retention in arid region is an input required parameter in precision water management at large scale.
-
9) Calculation of internal water resources for assessing the sufficiency and deficiency of local users.
-
10) Predicting of peak discharges, natural hazards and risks during the global climatic and antropogenic changes.
The hydro-meteorological data are taken from statistical measurements of Ministry of Ecology and Natural Resources of the Azerbaijan Republic, data of ungauged area were obtained with GIS technology taking into account DEM features of gauged stations and interpolating of climate data.
Results and discussion
At present, there is the tendention in world hydrology science when is estimated the AMC are widely used the concepts reflecting the multi-annual humidity conditions of territory. We have also tried to assess the AMC based on the multi-annual climate and other physico-geographical components. In order to test the runoff-forming possibility of precipitation we have used the obtained results of surface runoff coefficients with investigation over 29 river basins of the southern slope of the Greater Caucasus based on rational method and GIS technologies previously. The comparison of actual runoff data with data obtained using a rational method and GIS show that the error percentage ratios of 22 rivers from 29 has been under ±10%, only 7 rivers around ±10-15%. The small errors of actual and obtained data of the results show reliability and use possibility of the method proposed by us.
First of all, the changes of values S and Ia were verified which they determine the AMC condition on formation of surface runoff. For this purpose using GIS technology were carried out:
-
1) The "Precipitation", "Potential evaporation" and "Soil moisture" maps of the Azerbaijan Republic have been joined and based on combined maps the "Humidity coefficient" map (HCM-1) has been compiled. The humidity coefficient (R) is determined with the ratio of precipitation (P) to potential evaporation (E).
-
2) Based on the observated data of the precipitation, potential transpiration and soil moisture interpolated and processed with GIS and the actual "Humidity coefficient" map (HCM-2) was created. In order to obtain more reliable results the HCM-1 and HCM-2 maps are joined and reclassificated, based on their average results the HCM-3 was compiled.
-
3) The maximum retention (S) is calculated by the equation S=E-F, because the potential evaporation (E) participates for the loss of surface runoff, but soil actual moisture (F) as its yield. Potential evaporation-is defined as the amount vaporization of that would occur if a sufficient water source were available.
-
4) Based on the humidity coefficients obtained with processing of total results of the re-unification of LULC, HGS and DEM mapping data with a map HCM-3 data the AMC condition of territory was determined. We considered it acceptable to assume the humidity conditions of AMC I in the case of R≤0.8, AMC II R≥0.8-2.0 and AMC III R≥2.0 in the study area.
-
5) In finally, the initial abstraction was calculated in the traditional way on the basis of value S with the formula I a =λS for 3AMC conditions.
In accordance with the runoff formation and humidity conditions, the southern slope of the Greater Caucasus are divided into 11 humidity zones. The results on the divided zones are reflected in the table 3 and figure 1.
Table 3
The water balance elements on the humidity zones
|
Zones |
P |
E |
R |
F |
S |
λ |
I a |
|
I |
200 |
1150 |
0.17 |
15.0 |
1135 |
0.3 |
340.5 |
|
II |
250 |
1100 |
0.23 |
18.8 |
1081 |
0.3 |
324.3 |
|
III |
300 |
1050 |
0.30 |
22.5 |
1028 |
0.3 |
308.4 |
|
IV |
400 |
1000 |
0.40 |
30.0 |
970 |
0.3 |
291.0 |
|
V |
550 |
900 |
0.61 |
68.8 |
831 |
0.3 |
249.3 |
|
VI |
650 |
850 |
0.76 |
114 |
736 |
0.3 |
220.8 |
|
VII |
850 |
800 |
1.06 |
170 |
630 |
0.2 |
127.0 |
|
VIII |
1000 |
700 |
1.43 |
215 |
485 |
0.2 |
96.8 |
|
IX |
1300 |
650 |
2.00 |
293 |
358 |
0.2 |
71.6 |
|
X |
1500 |
550 |
2.73 |
360 |
190 |
0.1 |
19.1 |
|
XI |
1650 |
500 |
3.30 |
454 |
46,3 |
0.1 |
4.63 |
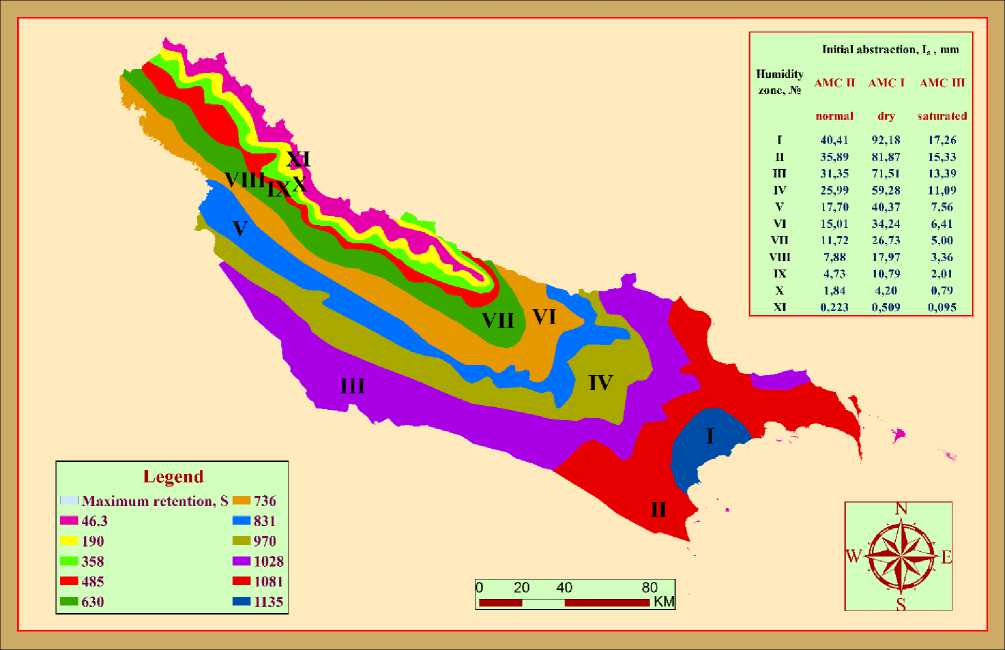
Figure 1. Humidity zones divided into the southern slope of the Greater Caucasus
The water resources and runoff values first of all depend on humidity conditions of territory (HCT). The precipitation and evaporation (temperature) are the main factors for determination of HCT. We have studied HCT both multi-annual changes and special moisture situations. The data within 11 humidity zones was given on the basis of the average annual values and is designed to evaluate the long-term HCT. And the average long-term results are obtained from the amount of precipitation and runoff occurring in concrete situations. Thus, a runoff generation mechanism is a very complicated process, because the rainfall can occur at any time, in any amount and different humidity conditions. The relationship between I a and S, I a and R was studied for define to runoff-forming process within concrete humidity condition and precipitation amount.
It is known, the initial abstraction can be expressed as a function of maximum retention Ia=λS and SCS have recommended Ia=0.2S from their experiences for normal AMC II moisture condition. The relationship Ia=0.2S was derived from the study of many small, experimental watersheds. Since the history and documentation of this relationship are relatively obscure, more recent analysis used model fitting methods to determine the ratio of Ia to S with hundreds of rainfall-runoff data from numerous U.S. watersheds. In the model fitting done by Hawkins et al. (2002) found that the ratio of I a to S varies from storm to storm and watershed to watershed and that the assumption of λ=0.2 is usually high. More than 90 percent of λ coefficients were less than 0.2. However, due to concerns such as not accounting for regional differences or scale effects, is required a separate approach to each area.
The investigations to determine concrete value of the runoff forming precipitation in a wide range have spread in the other countries, but there is still no unit scientific approach in this sphere. The study carried out in different countries (Egypt, USA, Uruguay, Greece, India, China, Canada, Australia, etc.) and in various climatic and geographical conditions also showed a change in the coefficient λ in a rather wide size (Baltas, E.A.,et al, 2007; Mishra S.K., Singh V.P.).
Therefore, it is appropriate to the initial abstraction coefficients to evaluate I a =λS only 3 AMC conditions would not be the right approach to this issue. We also studied the runoff-forming ability of precipitation specifically for each situation testing by the relationshep I a =λS in different moisture condition parts of the investigated area. The final resuls for destination of relationship between initial abstraction and coefficient humidity (λ=f(R)) was calculated by GIS technology with the average valuations are received the comparison and conversion of the data reclassification map (HCM-3), "Surface runoff map" and actual observated values of different river basins. The joint processing of the humidity coefficient together with the LULC, HGS and DEM data using GIS enabled to check the results in the 1568160 variations. As a result investigation, a high correlation and dense functional relationships between humidity coefficient (R) with initial abstraction (Ia) and its coefficient ( λ ) is defined (figure 2 and table 4).
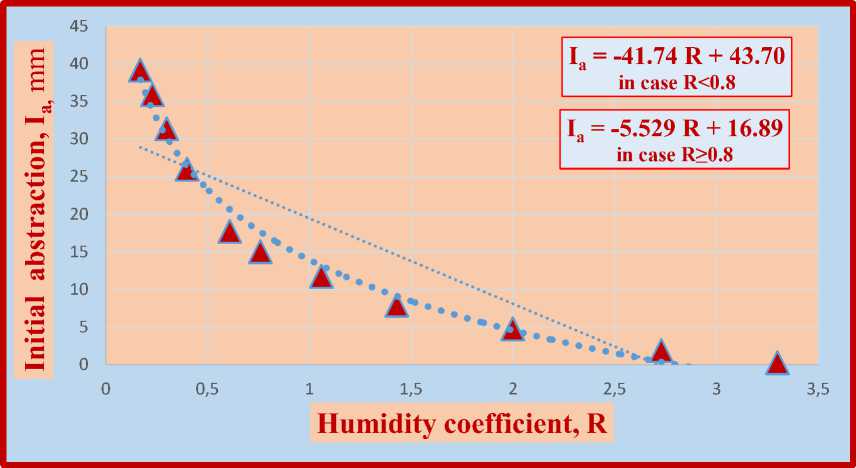
Figure 2. The relationship I a =f (R)
Table 4
The relationship between the humidity coefficient (R) and the initial abstraction coefficient (λ)
|
R |
λ |
R |
λ |
R |
λ |
|
≤0,10 |
0.450 |
0.51-0.55 |
0.230 |
0.96-1.00 |
0.190 |
|
0,11-0,15 |
0.400 |
0.56-0.60 |
0.223 |
1.01-1.10 |
0.185 |
|
0,16-0,20 |
0.350 |
0.61-0.65 |
0.216 |
1.11-1.20 |
0.180 |
|
0,21-0,25 |
0.325 |
0.66-0.70 |
0.210 |
1.21-1.30 |
0.175 |
|
0,26-0,30 |
0.300 |
0.71-0.75 |
0.205 |
1.31-1.50 |
0.165 |
|
0,31-0,35 |
0.280 |
0.76-0.80 |
0.203 |
1.51-2.00 |
0.150 |
|
0,36-0,40 |
0.265 |
0.81-0.85 |
0.200 |
2.01-2.50 |
0.130 |
|
0,41-0,45 |
0.252 |
0.86-0.90 |
0.198 |
2.51-3.00 |
0.100 |
|
0,46-0,50 |
0.240 |
0.91-0.95 |
0.195 |
≥ 3.00 |
0.050 |
With the aim of obtaining a higher correlation of the ratio Ia=f(R) in the cases R˂0.8 and R≥0.8, separate formulas were proposed in the forms:
I a = - 41.74 R + 43.7 (r2=0,9699) ─ in case R˂0.8 (7)
I a = - 5.529 R + 16.89 (r2=0.9717) ─ in case R≥0.8 (8)
The runoff-generation rate of precipitation (or changes of initial abstraction) under specific humidity condition (by 3 AMC's) in each zones was found using the GIS calculation and comparison programs and is shown in table 5: Table 5
Changes of the initial abstraction values within 11 humidity zones
|
Humidity zone, № |
Maximum retention, S, mm |
Coefficient initial abstraction, λ |
Initial abstraction, I a , mm |
||
|
AMC II |
AMC I |
AMC III |
|||
|
normal |
dry |
saturated |
|||
|
I |
114.1 |
0.354 |
40.41 |
92.18 |
17.26 |
|
II |
109.3 |
0.328 |
35.89 |
81.87 |
15.33 |
|
III |
105.9 |
0.294 |
31.35 |
71.51 |
13.39 |
|
IV |
96.8 |
0.268 |
25.99 |
59.28 |
11.09 |
|
V |
82.9 |
0.213 |
17.70 |
40.37 |
7.56 |
|
VI |
73.4 |
0.204 |
15.01 |
34.24 |
6.41 |
|
VII |
62.8 |
0.187 |
11.72 |
26.73 |
5.00 |
|
VIII |
49.0 |
0.161 |
7.88 |
17.97 |
3.36 |
|
IX |
36.1 |
0.131 |
4.73 |
10.79 |
2.01 |
|
X |
18.9 |
0.097 |
1.84 |
4.20 |
0.79 |
|
XI |
4.62 |
0.048 |
0.223 |
0.509 |
0.095 |
Application of investigation results
Thus, using the results of the proposed method may be estimate easily the generation state of rainfall to direct surface runoff (initial abstraction) in any area.
I direction . Using the rational method and multispectral analysis of satellite image of any territory is possible calculate surface runoff and initial abstraction. In the example below, we have reviewed the runoff-forming process after rainfall, choice a small area in the Gakh district. The land area is 1.07 km2, the average height is 466.0 m. (figure 3).

Figure 3. The satellite image of investigated area (1) and the image obtained with its multispectral analysis (2)
Initially, the rational (surface) runoff coefficient is found on the basis of LULC, slope and HSG (Hydrologic Soil Groups) data. The data of base factors were processed using GIS by following ways: the LULC-with the multispectral analysis of space image; the slope-with DEM prossessing, the HGS-with the soil texture by mechanical analysis. The area slope persentage is mainly the gradation of 2-6%, the HGS has within the C and D groups. With combining and reclassification of polygons (sub-regions) differented every 3 index and obtained new data has been found the avarage surface runoff coefficient of area (c=0.281). The first received results indicate the normal humidity condition (AMC II).
We will check the scale of runoff-forming share of precipitation of given area:
-
1) Suppose that in September and 25.3 mm of precipitation fell in this area, in that case the surface runoff found with rational coefficient (c=0.281) will be Q s = 0.281×25.3=7.11 mm.
-
2) On based given precipitation and surface runoff for AMC II condition by the traditional equations (2 and 3) S=31.65 mm and I a =6.33 mm were calculated.
-
3) Is determined AMC II (normal) on based total 5-day antecedent rainfall (table 1). If necessary, is passed to the other AMCs (AMC I and AMC III) conditions (the formulas of 5 and 6). So, if it falls over studied area 25.3 mm rainfall, within high humidity (AMC III) condition-2.70 mm, in the case of normal humidity (AMC II)-6.33 mm, in dry situation (AMC I)-14.4 mm precipititation may be create the surface runoff.
II direction. We also proposed a simple calculation way without using a rational method.
-
1) Are found the maximum retention value for the AMC II condition based on rainfall data (or both rainfall and temperature) of any area in the following equations:
S = - 0.9156 P + 1.855 t° + 1318 (r2 = 0.8937)(9)
S = -16.25 N – 0.8959 P + 186.1 (r2 =0.9981)(10)
S = -12 N - 0.1588 P - 0.2621 t° + 154.2 (r2=0.9448)(11)
Where, P-is rainfall, mm; t°-is tempurature,°C; N-is number of humidity zones (figure 1). The basis results are obtained by the rational method, as in the context of this direction, in fact, were taken into account complex of factors (landscape, slope, mechanical composition of the soil, etc.) and humidity zones features. Therefore, regardless of the spatio-temporal changes the received results are high reliability. Obtaining the correlation coefficients about 1 proves this thesis (the formulas of 9, 10 and 11). However, the accuracy of the results from a small area of the territory (under 8-10 km2) will be much higher (Fetter C.W, 2001).
-
2) Is found the initial abstraction from its relationship of maximum retention for AMC II (normal) humidity conditions:
I a (II) = -7.442 N – 0.2948 S + 82.25 (r2=0.9902) (12)
-
3) Are determined the 3 AMCs based on the fitting month and total 5-day (15-day) antecedent rainfall. If necessary, using the formulas of 5 and 6 are passed to AMC I and AMC III humidity conditions.
The estimation sample of the initial abstraction value
-
1 ) Let's suppose that 15 mm of precipitation fell in the area located in VII humidity zone on February 24. In this case the maximum retention calculated by the equation 10 will be S=58.91 mm.
-
2 ) It is the initial abstraction are defined with its relationship between the maximum retention for AMC II (normal) conditions (equation 12): Ia (II) =12.79 mm.
-
3 .a) If the 5-day antecedent rainfall on the territory is less than 12 mm is accepted as AMC I condition and Ia (I) =29.17 mm. (table 1 and equation 5). 15 mm rainfall is not able to create surface runoff such a situation and it’s also necessary at least 14.17 mm, there is Qs=P-Ia=15-29.17= - 14.17 mm rainfall shortage in this case. Because when Ia ≥P, the surface runoff does not form.
-
3 .b) If the previous 5 days of rainfall is 12-28 mm, the AMC II condition will be considered, Qs=P-Ia=15-12.79 = 2.21 mm of rainfall will be expended to surface runoff.
-
3 .c) If rainfall is higher than 28 mm, will be created the AMC III condition (table 1 and equation 6); I a (III) = 5.46 mm of rainfall is satisfactory for the initial abstraction. Q s = P-I a = 15-5.46 = 9.54 mm of rainfall will be consumed to surface runoff in that day.
Conclusions
-
1) When assessing the rate of runoff formation process, water resources and natural risks, is considered a key factor the humidity condition of the territory. In accordance with the runoff formation conditions, the southern slope of the Greater Caucasus are divided into 11 humidity zones. For each of the zones considering 3 AMCs, it’s possible to estimate water resources, runoff generation level and losses, maximum retention, initial abstraction and other water balance components for both the multi-annual term and the specific period. The research results are obtained by processing of complex runoff-forming factors using GIS technology, there are high accuracy and their application is possible in solution the major water-related issues.
-
2) For estimation the maximum retention (S), which the main parameter on the assessment of water-related values we proposed the following formulas on based its relationships with precipitation (P), temperature (t°), number of humidity zones (N):
S = - 0.9156 P + 1.855 t° + 1318 (r2 = 0.8937)
S = -16.25 N – 0.8959 P + 186.1 (r2 =0.9981)
S = -12 N - 0.1588 P - 0.2621 t° + 154.2 (r2=0.9448)
-
3) The calculations for determine of the runoff-forming share of precipitation (Ia-initial abstraction) may be used easily both by the analysis of multispectral satellite images of the territory using rational method, and by the relationships λ=f(R) (table 4), or I a =f(R) offered by us
I a = - 41.74 R + 43.7 (r2=0.9699) ─ in case R˂0.8
I a = - 5.529 R + 16.89 (r2=0.9717) ─ in case R≥0.8
Thus, using the results of the method proposed by us may be estimate and predict easily the formation state of rainfall to direct surface runoff, water resources and their loss risks in any territory.


