Theorem on uniform continuity of cononical potential

The theory of generalized functions is a basis for progress in many areas of mathematics and finds extensive applications in physics. One of the subdivisions of mathematics which is strongly influenced by the theory of generalized functions is the theory of subharmonic functions. Using generalized functions Azarin [1] constructed a theory of limit sets of subharmonic functions and measures, which is a significant contribution to the theory of subharmonic functions.

The best-known result in this area belong to Hormander [7]. In particular, he proved that the convergence of a sequence of subharmonic functions in a domain G as a sequence of the theory of generalized functions in G is equivalent to the convergence in the space ^ m,Zoc ⁽y^{; £) .}

We will use the following notation:

B ( z ₀ ; R ) = { z e C : | z - z ₀| <  R } ; CB ( z ₀ ; R ) = CIB ( z ₀ ; R ).

In the theory of subharmonic and 5 -subharmonic functions in the plane C, an important role is played by the kernel:

(  ( z z        1 z p ^

K(z;Z) = Re In 1--+ - +... +--, pp

V V ^Z 7 ^z       p ^z 7

where p £ N. For all z , Z e C we have the inequality ([8], Lemma 2):

I K p ( z ; Z )| <  M ( p )

I Z

I z i p      • I

—— min<

1;

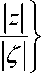
where M(p) depends only on p. Let y be the Radon measure in C . We consider the following potential

K ( z ) = J K p ( z ; Z ) d / ( Z ),

C which we shall call the canonical potential of the measure y .

In this paper, we consider this Cononical potential K ( z ) as a map from the space C into the space L ( C ; B y ( Z )) . In this case, we can write K ( z ): C ^ L ( y ).

The convergence of a sequence u_n ( z ) to u ( z ) in the space L_m ( y ; C ) means the following. If y is the restriction of the Lebesgue measure to a compactum K contained in the space C, then JJ U( ( z ) - u ( z )| ^ y ( z ) ^ 0 ( n ^ да ).

We state several well-known results obtained in this area. We have already mentioned Hormander’s proposition [8]. Hormander considered the multidimensional case; we consider the case where the dimension of the space is m = 2 , although the requirement m = 2 is not essential in many of our arguments. It is important for what follows that the dependence of K ( z ) on z be uniformly continuous.

In the present paper we find sufficient conditions on a measure y with support compactly embedded in G that guarantee the convergence in the space L_m ( y ; C ) of sequences of subharmonic functions that converge in the sense of the theory of generalized functions.

We state several well-known results obtained in this area. We have already mentioned Hormander’s proposition. Hormander considered the multidimensional case; we consider the case where the dimension of the space is m = 2, although the requirement m = 2 is not essential in many of our arguments. The following was proved in [10], Theorem 5. Suppose that yn is a uniformly compactly supported sequence of Borel measures, supp y с C, and the measures Yn have uniformly bounded variation and weakly converge to the zero measure.

The uniform continuity of these functions is a restriction on the measure у which appears in the theorems that are the principal results of the paper. It is important for what follows that the dependence of K ( z ) be uniformly continuous.

Theorem. Let m > 1 be an arbitrary fixed number. Suppose that у is a positive finite Borel measure with compact support that satisfies the condition supp у с C. In addition, suppose that sup <

K p ( z ; Z ) = Re

ln 1 - -

I I z

z

+ Re — +... +

I Z

p

¹ — = In 1 - z + K *( z ; Z )

p Z ^p )       Z p

Obviously the function K_p ¹ ( z ; Z ): C ^ L_m ( y ) is uniformly continuous with respect to the variable z in the space ℂ .

• 2.    We set

И^ z 2 ) = J I In I z i - C I - In I z 2

p

- Z II d / ( Z )

V" ^p          (,

; F ( z ) = J |ln|z - Z || ^pd / ( Z )

X 1' p

•

Since the Logarithmic potential as a function from ℂ into ℝ, is not bounded, we need to prove the convergence of the integrals introduced above. We do this at the first stage. It follows from the Minkowski inequality that

F ( z ) <

J |ln|z- CW-WO к B (z;5)

\ 1' p

\ 1' p

J |ln|z - Z 11 -ад к CB (z;5)                          7

= J + J ₂.

where CB ( z ; 5 ) = C \ B ( z ; 5 ) .

We prove that the inequality

I lnIz - Z I|< ln ^—                                               (3)

О holds for sufficiently small 5 and for Z e (supp /)П CB(z;5). From the inequality

• (3)    we obtain that J <  ln— ( / ( C ) ) 1' ^p . By the hypothesis of the theorem, J <  1 for ²       5                                                                      ¹

• 3.    We prove that the inequality

sufficiently small 5 . Hence, F ( z ) is finite. What has been proved can also be stated as follows: for any z e C the function K ( z ) is an element of the space L_p ( / )• The inequality ^ (z,; z ₂) <  F ( z_x ) + F ( z ₂) implies that ^ (z,; z ₂) is finite.

I V z lnI z - Z I|< —•                                               (4)

holds for | z - Z | ^ 5 .

Let z = x + iy ; ^Z = n+ ^{i T} we have (^ln| z - ^Z |) ‘ n =^- р Х^^ т ; ( ln l ^{z - Z} l ) T =^- y -T^

From these estimates it is easy to obtain inequality

2                   A2

^V z lnI z - Z hl ( ln | z - Z |) , ) +l ( ln| z - Z l) , )

------< -.

I z - Z I 5

Thus the inequality (4) is proved.

• 4.    This is the most essential part of the proof. We claim that

^ (z ^z 0 ) ^ ^{0     (} z ^ z 0 )

Let 5 be an arbitrary number. We assume that the inequality z - z ₀| <  5 holds. Consecutive application of the Minkowski inequality [4] and the inclusion B ( z ₀ ;2 5 ) c B ( z ;3 5 ) yields

^ (z; ^z o ) <

1/ p

J   |ln|z - Z || - d _Y (Z )

_v CB ( z ;3 5 )                             _v

+

1/ p

J   |ln| z - Z | - ln| z o - ZW'd^^ )

V CB ( z o ;2 5 )                                                _v

+

1/ p

+

J    |ln|z o - < || p d / ( Z )

= J, + J + J .

_v CB ( z o ;2 5 )                                 _v

If Z £ B ( z ₀ ; 2 5 ) and | z - z ₀1 <  5 , then the inequalities w - Z | >  5 and

|V^ In | z - Z || <  1     hold for any w e B ( z ₀; | z - z ₀1) .

The estimate of the gradient implies that

I^{ln| z - Z} | ^{- ln| z} o ^{- Z} || <¹ | ^{z - z} o|; J 2 < ¹ ( Y ( C ) ) '/ p|^{z - z} o| •

From the hypothesis of the theorem we obtain that

J ^ 0; J3 ^ 0 (5 ^ 0), which proves the required assertion.

The collection of assertions that we have obtained is contradictory. Thus the theorem is proved.

Example. Let y be a Lebesgue measure in the space ۥ We will use the standard notation d Y = dxdy . Consider the integral in the condition (2) and, making a parallel translation, we obtain the equality for Z = x + iy :

J = J |ln | z - Z |I ^P dxdy = J |ln | Z |I p dxdy .

B ( z ; 5 )                              B (0; 5 )

We introduce polar coordinates:

We obtain the equality:

x = r cos ф

y = r sin ф

J = J J r |ln r|^P drd ф = 2 n J r |ln r|^P dr .

2 n 5

It is obvious that condition holds for arbitrary p : J ^ 0;     ( 5 ^ 0) .