Theoretical substantiationof the Meissner effect

The Meissner effect, by definition , is that the magnetic field is completely displaced from the volume of the superconductor [1]. It is generally accepted that this effect serves as experimental proof that there is a fundamental difference between the internal structures of a superconductor and an ordinary conductor. Further, it will be proved that this effect is a consequence of high electric currents, and not the specificity of the material.

First of all, consider a great experiment [2]. A superconducting disk hangs over a flat ring of magnets and moves along this ring, as if along rails, if the experimenter pushes it slightly. This is shown in Figure 1. The superconductive disc also hangs under the ring of magnets, and is also held next to the tilted magnet at any angle of inclination of this magnet. This is shown in Figure 2. It is quite obvious that neither repulsion nor attraction between the disk and the magnet can explain this experiment. The concept of magnetic expulsion does not help to find an explanation. The effect exists but the generally accepted definition of this effect was contrived for a contrived explanation. This is what is called result fitting.

Fig. 1.

Fig. 2.

Thus, the Meissner effect should be defined as the position of a conductor next to a magnet without any touch between them, stable and independent of the orientation of the magnet and the relative velocity of movement of the conductor.

This means that not only the fact of repulsion but also the fact of attraction between the magnet and the conductor needs to be explained . Gravitational force cannot be an explanation for the attraction of the conductor from below and from the side. Therefore, further we will neglect the force of gravity.

2.    Conductive disc next to the magnet

The following section proves that in a conducting disk under the action of a constant external magnetic field

• •    there is a constant electric current,

• •    this constant electric current in the cylindrical coordinates propagates along the radius, along the circumference, and along the axis of the disk,

• •    the current arises despite the fact that the disc is not a closed conductor along both the radius and the axis,

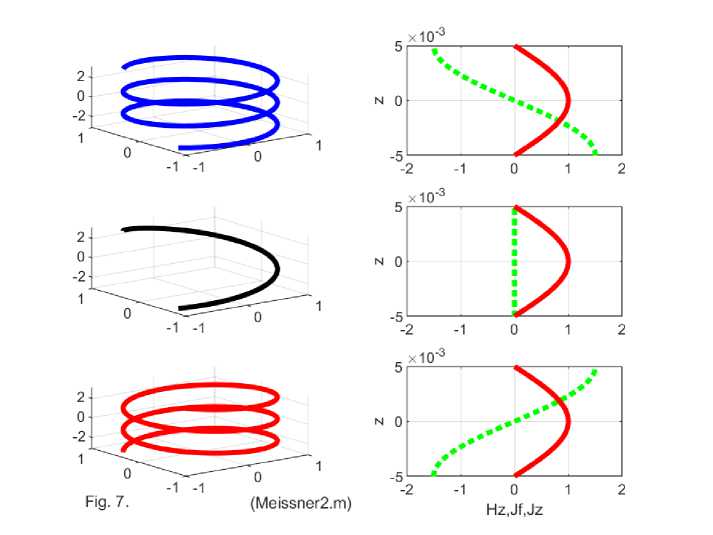
• •    streamlines have a spiral structure,

• •    around the circumference, the current can rotate in one direction or another, or not at all.

3.    Appendix: constant electric current structure

Thus, we can say that a conducting disk in the field of a permanent magnet is a solenoid. This solenoid interacts with the magnet, i.e. the magnet creates the solenoid that interacts with this magnet.

Ring electric currents generated in the disk create an axial magnetic field strength directed against the magnetic field strength of the magnet and therefore, the disk is repelled from the magnet. This is consistent with Lenz's rule. As the distance between the disk and the magnet increases, the external strength acting on the disk decreases and the magnitude of the currents decreases. First of all, the magnitude of the ring currents decreases and the force of repulsion of the disk from the magnet decreases. At some point, the ring currents become equal to zero. If the disc continues to move away from the magnet, then the ring currents reappear but directed in the opposite direction, and the disc is attracted to the magnet. Thus, the position of the disc at the point of zero ring current is stable.

So, in the disk contains a solenoid with a current. Each element of the conductor with a current is affected by the Lorentz force as the result of the vector product of the current element and the induction of the magnet.

The horizontal projections of the Lorentz forces are summed up. The reader can be convinced that the sum of these forces becomes equal to zero when these forces are located symmetrically relative to the solenoid axis. This position is created when the axis of the solenoid coincides with the axis of the magnet. Consequently, the Lorentz forces position the solenoid so that its axis coincides with the axis of the magnet.

From the above it follows that a solenoid with a current arising under the action of a magnetic field is located at a certain distance from the magnet, and its axis coincides with the axis of the magnet. Thus, a conductor located next to a permanent magnet can exhibit the Meissner effect. This effect will be the greater, the lower the resistance of the conductor. Not surprisingly, this effect has been discovered in experiments with superconductors. However, this effect is NOT a consequence of superconductivity.

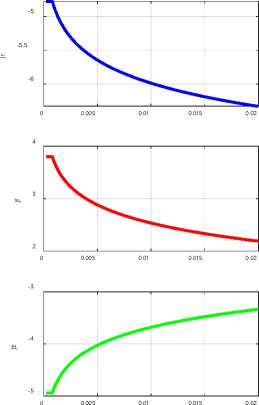
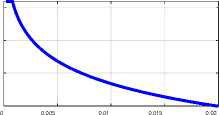
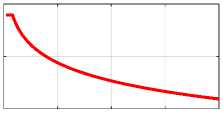
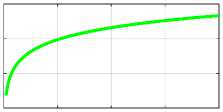
In Chapter 5 of Ref. [1], it is shown that in a constant electric current wire the distribution of both the current densities J and the magnetic strengths H is described by Maxwell's equations, which in this case have the following form:

rot(H) = 0,(1)

div(H) = 0.(2)

rot(j) = 0,(3)

div(J) = 0,

In our modeling, we will use the cylindrical coordinates г, ф, z . Then these equations will take the following forms:

Hr . QHr . 1 d^ . 9HZ = 0 r    dr r Эф    dz     ’ (5) 1 dHz  dHф = J r Эф    dz    Гт ’ (6) dHT   dHz —_—=Jф ’ (7) H0 . ЭИф _ 1 dHr = j r     dr    r Эф Zz ’ (8) Jr . d Jr . 1  dJф  . dJz __ 0 r    dr r  Эф    dz     ’ (9) 1.921_Э2ф = 0 r Эф    dz     ’ (10) dJr   dJz   0 dz dr      ’ (11) Jф + dJф 1 dJr = 0 r    dr r Эф     . (12) The solution to this set of equations is: Hr = hr- (r)sin( окр + /z), (13) H

h'Z ⁽r) + h'z ⁽r) - h_z⁽r) (^ + %²) = 0, (19) h_V (r) = "(^ Jr (r)), (20) hr⁽r) = — Z ^^z⁽r) + ]ф(r)), (21) ^jZ^{(r)+ j}Z^(r)1-Jz ^(r) fa + %²) = ^0, (²²) 70 (r) = "~> (23) ^jr ⁽r) = Ч'Ь⁽r)" (24)

Fig. 3 (Meissner.m)

0               0.005                 0.01               0.015                 0.02

0               0.005                 0.01               0.015                 0.02

r

Fig. 3.

It is important to note that in this case, eight equations (5)-(12) also have a unique solution in the form of six equations (19)-(24) for fixed values of the parameters a, %. Figure 3 shows the graphs of the logarithms of these functions for a = 0.5, % = 0.1,7? = 0.02.

Both the currents and the magnetic strengths are always distributed this way, even if only thermal currents exist in the wire. This is so because the currents interact with each other by the Lorentz forces and Maxwell's equations describe namely this interaction. If the conduction current is added to the thermal currents, then in the mathematical description only the values of the constants a, % change. Exactly the same happens when the wire enters an external magnetic field: only the values of the constants a, % change. A change in the magnetic field only changes the values of the constants. It is important, however, that the magnetic field strength is uneven. In Chapter 5d of book [3], various experiments are described that demonstrate the phenomenon of the appearance of a constant electric current under the influence of a constant magnetic field.

Thus, the magnetic field in the wire is not displaced but is created again and the currents are created along with this field. When the internal resistance of the disk is low, the currents take on large values.

The current in the wire has a solenoidal structure. Therefore, the reader can consider it as a solenoid. Figure 4 shows three helical streamlines: the thick blue line for a = 2, % = 0.8, the middle green line for a = 0.5, % = 2, and the thin red line for a = 2, % = 1.6. The helical lines are shown for the functions J determined by (17) and (18), namely for the total current with the projections /^ and J_z for r = const. These functions are defined for a > 0.

Fi 1                           -1        -1

Fig. 4.

Fig. 1P.

(TokPotok33.m)

-1      -1

Fig. 5.

Figure 5 shows the helical lines

•

•

for the functions J defined for a > 0 (similar to the case shown in Figure 4) and shown by the thin blue line in Figure 5 and for functions J defined for a< 0 and shown by the thick red line in Figure 5.

For a > 0, the circumferential currents disappear: see the function j, (r) in formula (23). However, equation (4) is still valid. For a > 0, the sign of the function H_z also changes, see (15).

All equations are also valid for a wire of limited length, for instance, for a disk in our case. Figure 6 shows functions (13)-(18) on the wire of the length of L = -A It can be seen that the axial current J_z (solid red line) is equal to zero at the ends of the wire. Also, both the axial magnetic strengths H_z and the circular current J^ (dashed blue line) at the ends of the wire take maximum and opposite values.

1.5

-5

-3

z Fig. 6 (M

Fig. 6. (Meissner.m)

In fig. 7 shows the various functions for the three positions of the disc, assuming the magnet is on top, with the functions for the stable position shown in the middle windows. Functions shown for only one radius value. The right-hand windows show the streamline spiral, while the right-hand windows show the Z-dependent function J_z (solid line) and the H_z , J<p functions (dashed line).