Theoretical Validation of Inheritance Metrics for Object-Oriented Design against Briand's Property

Published Online June 2014 in MECS

Nowadays, the uses of Object-Oriented (OO) software metrics have increased rapidly. So, software metrics is the essential to measure the software quality factors. A good software metrics should be validated for its use. In order to provide mathematical rigour and an axiomatic basis to metrics, necessary properties have been set forth by Weyuker [1] and Briand [2] against which metric proposals can be evaluated. Few of the inheritance metrics have been validated using Briand properties. Evaluation of metrics against Briand measurement concepts provides insights into the characteristics and defects of the metrics. Besides serving as a tool for classification and understanding, property based evaluation can also potentially lead to formulation of new metrics. Sandip et al [3] [4] and Rajnish et al [5] [6] proposed four Inheritance metrics and validated using Weyuker properties. This paper shows the validation of the metrics using Briand properties.

For OO systems, most of the inheritance metrics have been validated theoretically by Krishna et al [7] and Joshi et al [8] using Briand properties. Metrics exist for measurement of inheritance at the higher levels of abstraction in OO systems has been given in [3-6]. Rajnish had presents a new class complexity metric of an OO program which is used to predict the understandability of classes in software projects. Their propose complexity metric is evaluated theoretically against Weyuker’s properties to analyze the nature of metric and empirically evaluated [9].

Various inheritance metrics have been proposed and their reviews are available in the literature. Chidamber and Kemerer [10] proposed the DIT metric, which is the length of the longest path from a class to the root in the inheritance hierarchy and the NOC metric, which is the number of classes that directly inherit from a given class. Henderson-Sellers [11] suggested the AID (average inheritance depth) metric, which is the mean depth of inheritance tree and is an extension of Chidamber and Kemerer DIT. Li [12] suggested the NAC (number of ancestor classes) metric to measure how many classes may potentially affect the design of the class because of inheritance and NDC (number of descendent classes) metric to measure how many descendent classes the class may affect because of inheritance. Li [12] also theoretically validated Chidamber and Kemerer metrics using a metric evaluation framework proposed by Kitchenham et al [13] and discovered some of the deficiencies of Chidamber and Kemerer metrics in the evaluation process and proposed a new suite of OO metrics that overcome these deficiencies. Tegarden et al. [14] proposed the CLD (class-to-leaf depth) metric, which is the maximum number of levels in the hierarchy that are below the class and the NOA (number of ancestor) metric, which is the number of classes that a given class directly or indirectly inherits from. Lake and Cook [15] suggested the NOP (number of parents) metric, which is the number of classes that a given class directly inherits from and the NOD (number of descendants) metric, which is the number of classes that directly or indirectly inherit from a class. Alshayeb et al [16] empirically validated two different software processes. Agarwal et al [17-18] described the approach of empirical study of OO metrics and presented OO design metrics.

The rest of the paper is organized as follows. Section II describes Briand’s length and size properties for validating inheritance metrics. Inheritance metrics have been taken for evaluation is described in section III. Section IV describes viewpoint and projection of inheritance metrics presented by Rajnish and Sandip. Section V provides theoretical validation of inheritance metrics against Briand’s properties. Section VI presents Conclusion and Future work respectively.

• II.    Briand’S Size and Length Property

• A.    Size Properties

Size metrics are commonly found in OO approaches. Sizes are not bounded, and they are computed as positive integers. The three size properties namely non-negativity, presence of null value and module additivity as outlined by Briand et al. [2] are summarized in Table 1.

• B.    Length Properties

Length of a system is seen as size of the shortest path between two extremes of the system. Length is therefore

Table 1. Size Properties of Briand

Property Description S1 (Non-negativity) The size of a system is nonnegative. S2 (Null value) The size of a system is 0 if the set of elements which constitute the system is empty. S3(Module Additivity) The size of a system cannot be more than the sum of the sizes of its modules. In the case of disjoint modules, the size of a system is equal to the sum of the sizes of the modules. not the same as size, since it captures the size from the point of view of the extreme limits, whereas, size in general captures the measured as a whole. Lines of Code and CLD are examples of size and length metrics respectively. The length properties observed by Briand et al. [1] are summarized in Table 2.

Length properties L1 and L2 are the same as S1 and S2 respectively. Size metrics satisfy non-increasing monotonicity (L3) and non-decreasing monotonicity property (L4) , since adding relationships between the elements within a module or between the elements of different modules in the system does not change the count of the entities already present in the system. However, the considered size metrics do not satisfy module merger (L5) because the size metrics are sum oriented and not comparison oriented. Thus, it can be observed that metrics satisfying sum oriented size property S3 do not satisfy comparison oriented length property L5 .

Table 2. Length Properties of Briand

Property	Description
L1 (Non-negativity)	The length of a system is nonnegative.
L2 (Null value)	The length of a system is 0 if the set of elements which constitute the system is empty.
L3(Non Increasing Monotonicity)	Adding relationships between the elements of a module m in a system does not increase the length of the system.
L4 (Non Decreasing Monotonicity)	A system having modules m1 and m2 such that they are represented by separate connected components in the system. Adding relationships from elements of m1 to elements of m2 does not decrease the length of system.
L5 (Merger)	The length of a system made of union of two disjoint modules m1 and m2 is equal to the maximum of the lengths of m1 and m2 .

• III.    Inheritance Metrics for Evaluation

This section presents the brief description of Depth of Inheritance Tree of a Class (DITC) metric and Class

Inheritance Tree (CIT) metric presented by Rajnish et al. [5-6] AND ICC (Inheritance Complexity of Class), and ICT (Inheritance Complexity of Tree) presented by Sandip et al. [3-4] for evaluation.

• A.    Depth of Inheritance Tree Class (DITC) Metric

The metric DITC for class inheritance hierarchy is measured in terms of sum of the attributes (Private, Protected, public and inherited) and Methods (Private, Protected, public and inherited) at each level [6]. The DITC metric of a class at each level is calculated as:

CIT ( C ) = E           (1)

Where,

LEV i = Attribute (C i ) + Method (C i )

C i = A class in the i^th level of class inheritance hierarchy.

Attribute (C i ) = Count the total number of protected, private, public and inherited attributes within a class in the class inheritance hierarchy at each level.

Method (C_i) = Count the total number of protected, private, public and inherited methods within a class in the class inheritance hierarchy at each level.

L = Total height in the class inheritance hierarchy i.e. the maximum distance from the last node (last level in the class inheritance hierarchy) to the root node (first level in the class inheritance hierarchy), ignoring any shorter paths in case of multiple inheritance is used.

• B.    Class Inheritance Tree (CIT) Metric

The metric CIT is used to measure the class inheritance tree [6]. The primary purpose of this metric is to measure how class is inherited by multiple classes and how class inherits multiple classes at any level in the inheritance tree. CIT is defined as follows:

CIT (q) =_Z^ci_N(ci) ₊ cour(ci)

Where C_i is the class at the i^th level in the inheritance tree.

CIN (C_i) = 1 if C_i is inherits multiple classes in the inheritance tree.

= 0 , otherwise.

COUT (C i ) = 1 if C i is inherited by multiple classes in the inheritance tree.

= 0 , otherwise.

• C.    Inheritance Complexity of Class (ICC)

The metric ICC is given in [3] and is calculated as follows:

NoofclassesinheriteddirectlybyCi1 + NoofclassesinheriteddirectlybyCi

Where, Inheritance Complexity of Class (ICC) is the metric value of a class of an inheritance tree.

C_i = Classes at the i^th level in an inheritance tree.

A (C_i) = Count the number of attributes (protected, private, public and inherited attributes) at each level in an inheritance tree.

M (C i ) = Count the number of methods (protected, private, public and inherited attributes) at each level in an inheritance tree.

• D.    Inheritance Complexity of Tree (ICT)

The metric ICT is given in [4] and is calculated as follows:

.    M (C i ) + A (C i ) + IF (C i )

ICT (C i ) = ———--—     (4)

Where

2^7 c ■ _ Noof classes inherited directly by Ci1    + Noo f classes inherited directly by Ci

N = Total number of classes in an inheritance tree.

• IV.    Viewpoints and Projections

The notion of viewpoints and projections was first introduced in [8] to aid classification of metrics. Viewpoint is the base at which the measurement is carried out and projections shows direction of interaction between the viewpoint and the portion of the program that is related to the measurement. Projections can be outward, inward or gross projections. At the end of this paper in Appendix A , shows the viewpoints and projections of other inheritance metrics presented by Krishna et al [7] and selected four metrics as mentioned in Section III. All these four metrics generates value for each class at each level, so view point of each metric is class level. But each class links to its parent classes in DITC , so it has outwards projection. CIT metric is related to its parent classes and child classes, so it has gross projection. ICC and ICT metrics depends on all the classes in the system, so it is system viewpoint.

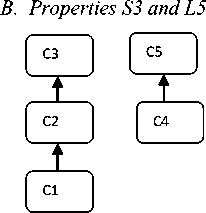
Fig.1: (a) Two disjoint module (b) After joining C1 and C4

Fig. 1 shows two disjoint modules, one have three levels ( C1 is in first level and C3 is in third level) and another have two levels ( C4 is in first level and C5 is in second level). After merging C1 and C4 , the class C1+C4 is in first level and C3 is in third level. Suppose every class has one method and one attribute.

DITC (C1) = 2*1 = 2

DITC (C4) =2*1=2

DITC (C1+C4) =4*1=4

DITC (C1) + DITC (C4) = 2 + 2 = 4 = DIT (C1+C4)

So, DITC metric satisfies size property S3 and does not satisfy L5 .

CIT (C1) = 0 , because C1 does not inherits multiple classes and it also does not inherited by multiple classes.

CIT (C4) = 0 , because C4 does not inherits multiple classes and it also does not inherited by multiple classes.

CIT (C1 + C4) = 1 , because C1 + C4 does not inherits multiple classes but it is inherited by multiple classes C2 and C5 .

So, CIT metric doesn’t satisfy property S3 and also not satisfy L5 .

IF (C1) = 1/2 = 0.5, IF (C4) = 1/1=1 and IF (C1+C4) = 2/2 =1

ICC (C1) = 1+1+ 0.5=2.5

ICC (C4) = 1+1+ 1=3

ICC (C1+C4) = 2+2+1 =5

• So,    ICC is not satisfied S3 and not satisfy L5 .

IF (C1) =1/2=0.5, IF (C4) = 1/1=1 and IF (C1+C4) = 2/2 =1

ICT (C1) = (1+1+ 0.5)/3=0.833

ICT (C4) = (1+1+ 1)/2=0.67

ICT (C1+C4) = (2+2+1)/4 =1.25

So, ICT is not satisfied S3 and not satisfy L5 .

• V.    Theoretical Validation against Briand’S Property

• A.    Properties S1, S2, L1 and L2

From the definition, it can be noted that for each metric there must be one positive or zero value. So, all the four metrics that have been described above is satisfied by Briand’s size property S1, S2 and length property L1, L2 .

• C.    Property L3

A class viewpoint metric satisfies property L3 , as the metric does not use the relations among the methods and attributes. Adding new relations among the methods and attributes does not change the metric value. So, all the four inheritance metrics ( DITC, CIT, ICC, and ICT) satisfied property L3 .

• D.    Property L4

Consider Fig.2 that is slightly different from Fig. 1. The difference is that add one relationship between C1 and C4 in place of merging of C1 and C4 .

DITC does not depend on relationship between two modules. So, DITC satisfy L4 .

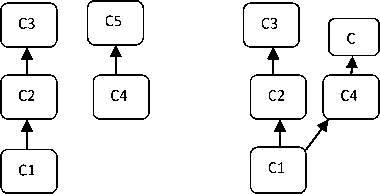
Fig.2: Two disjoint module and after adding relation between two disjoint connected modules

CIT (C1) = 0, when C1 and C4 are in different connected component.

But CIT (C1) = 1 , when add relationship between C1 and C4 . So, relationship may increase CIT value but never decrease.

IF (C1) =1/2=0.5, IF (C4) = 1/1=1 in different connected component, and IF (C1) = 2/3 =0.67

Before adding relationship ICC (C1) = 1+1+ 0.5=2.5

After adding relationship ICC (C1) = 1+1+0.67 =2.67

So, relationship may increase ICC value but never decrease.

Before adding relationship ICT (C1)  =  (1+1+

0.5)/3=0.833

After adding relationship ICT (C1) = (1+1+0.67)/5 =0.534

So, ICT is not satisfied L4 .

• VI. Conclusion and Future Scope

In this paper an attempt has been made to present a theoretical evaluation on Inheritance Metrics proposed by Rajnish et al [5-6] and Sandip et al [3-4] satisfy necessary properties of Briand et al [2]. At the end of this paper in Appendix B, summarizes the results found in this paper and another related paper [7]. The results show that DITC, CIT ICC, ICT metrics satisfies the necessary properties given by [2]. From Table 4 it is observed that out of 21 inheritance metrics, no metric satisfy all properties and all metric satisfy the property S1, L1, S2, L2, and L3. Only Specialization Ratio and ICT do not satisfy L4. So S1, L1, S2, L2, L3 and L4 are the necessary properties to validate an inheritance metric. Four system viewpoint metrics (ICC, ICT, Specialization Ratio, and Reuse Ratio) does not satisfy property S3 and L5. Fourteen metrics out of 21 (around 66%) satisfy property S3 and only 2 metric satisfy property S5. In general, this firmly belief that 67% of the considered metrics are satisfied Briand’s size property and 9% metrics are satisfied Briand’s length property. Only system view point metrics except CIT are not satisfied by Briand property. So class view point metric is always satisfying the Briand property. All other metrics have to be revised to comply with the Briand [2] properties. Otherwise, use of these metrics as inheritance indicators is questionable.

The future scope focuses on some fundamental issues: (1) the work also points at a need for further work on the scope of existing validation properties and also on measurement concepts that are relatively less explored. (2) Empirically explore the relationships between the theoretical and empirical validation results.

Acknowledgment

The author would like to thanks the anonymous reviewers for their valuable comments and suggestions.