Time dependence of the output signal morphology for nonlinear oscillator neuron based on van der pol model

Published Online April 2018 in MECS DOI: 10.5815/ijisa.2018.04.02

At present, intensive research on the application of neural networks is being conducted to solve a wide range of Data Mining tasks (identification of non-stationary chaotic processes, clusterization, classification, intellectual management, biosystems states diagnostics, prediction, emulation and recognition of multispectral input images). Considerable interest in the study of modern neurodynamics lies in the processes of information encryption, decryption and processing that is transmitted by neurons. In the early stages of sensory information processing Wavelet analysis is an effective tool to study the information component of the neural signals that are registered. Traditionally such research demands to analyze the structure of point processes, i.e. the time-frequency dynamics analysis of neural reviews [1]-[6], in which information carriers are times of pulses (spikes) generating, but not their form [7]. The mechanisms that lead to the spikes generation are partially known [8]. But how neurons and their ensembles transmit information about around world, so far has practically been unexplored.

In the wavelet-neurophase network, the waveletneuron is structurally close to the standard formal neuron with N inputs, but instead of the usual synaptic weights λ , there are wavelet-synaptic weights λWSi (i= 1,2,..., N) , in which the adjustable parameters are not only the weights λ , but also the scaling and offset wavelets. It should be noted that in all of the abovementioned artificial neural networks, neurons were considered without their own dynamics (their own frequency of oscillations of the neuron ω = 0 ) and without taking into account the accumulation of impulses N in the neurons that triggered when N≥ N (N is the threshold value of the k-th neuron pulses). The main advantages of self-developing artificial nonlinear neural networks is the ability to adapt to dynamic conditions and the speed of functioning, which is especially important when operating in real-time. In order to provide the highest class of efficiency (speed of operation) and the quality of the recognition of input spectral images, it is proposed to develop the architecture of self-developing artificial nonlinear neural networks and an algorithm for their training based on evolutionary simulation methods that can adapt to dynamic conditions when working in real-time.

Accordingly, to above-mentioned there is necessity to solve the following problems:

• •    It is necessary to suggest the method of inhomogeneous nonlinear differential equations with quadratic non linearity of the unknown function at the first derivative.

• •    It is necessary to define that nonlinear oscillator neuron can act as a frequency modulator, which can modulate the input information of non-stationary signal.

• •    It is necessary to determine that nonlinear oscillator neuron with threshold effect significantly alters the structure of the input information non-stationary signal different in shape, frequency and amplitude.

• •    It is necessary to determine the existence of resonance effects in nonlinear oscillator neuron when frequency of the external non-stationary signal and dynamics of the natural frequency of the neuron are equal.

• •    It is necessary to suggest information coding with nonlinear oscillator neuron on the basis of frequency modulation and decoding using an inverse operator, which acts on the output signal vector.

• II.    Related Works

In [2], [3], [6], the authors analyzed the case of signals conversion by sensory neurons (threshold device), but its own dynamic neuron was not taken into consideration. Using classical models threshold systems such as “integrate-and-fire” [2] and “threshold crossing” [3], [6], it has been shown that various characteristics of complex dynamics at the entrance sensory neuron are stored in the point process structure [2]-[6], [9]-[11], [17]-[33].

Computer neurons dynamics modeling when exposed to constant external signal was conducted in Van der Pol approaching [12]. The authors [13] investigated frequency-temporal dynamics of sensory neuron (threshold device) using the technology of double wavelet analysis and taking into account the interaction of its own dynamics and the dynamics that was caused by the influence of external non-stationary signal. In this sensory neuron was modeled as a threshold device that converts the input signal to pulse sequence output. This pulse sequence was described by the sequence of Dirac delta functions, each of which corresponds to the pulse (adhesions) generation moment. These model pulses have the same shape and amplitude, that’s why information about the external effect of dynamic signal appears only in the time intervals between the moments of their generation.

• III.    Setting Objectives

The aim of this work is to study the analytical and numerical method of time-frequency and timedependence of the output signal morphology for nonlinear oscillator neurons based on Van der Pol model taking to account threshold effect neurons when it is exposed to different in shape, frequency and amplitude of external non-stationary signals.

• IV.    Mathematical Model

Nonlinear oscillator sensory neuron type Van der Pol (threshold device) with its own dynamics ^k, which can generate pulses in the absence of external non-stationary signals (Vk (t) = 0), when the number of available sensory neuron impulses N reaches a threshold value N (Nok > Nck)was considered. Thus, such neuron can be considered as a threshold device that converts the input non-stationary signal V(t) into a sequence of pulses output (Fig.1) due to the “imposition” of the dynamics of input non-stationary signal V(t) on its own neuron dynamic. Consequently, the signals conversion process analysis by nonlinear oscillator sensory neuron is complicated. The complex dynamics of transformation of input non-stationary signal received by biological sensor with its own dynamics shows an experimental record signal (Fig.1b) [13]-[16]. This signal generated by a biological neuron without external signal action (interval 0< t <110s with a low-δ-pulse sequence). At the time interval 110s< t <200s shown on (Fig. 1b) the result of external signal interaction with the biological sensor with its own dynamics which leads the formation of high-order δ-pulses sequence.

To illustrate, let us consider encoding information by touch nonlinear oscillator k-neuron which describes the nonlinear equation of the form

X k + ^ .[ X 2 - p .N 0 k ; V . )] X_k + ^_QkX_k = V_k ( t )  (1)

where p2(N0k;Nck) = p2k tanh(N0k 2Nck)- setting the ^k amplitude of the k-th neuron; ^ > 0 ;

N_ok , N_ck , a2 are the number of pulses that come to k -th neuron, threshold pulse k -th neuron and variance respectively;

to 2 is natural frequency k -th nonlinear oscillator neuron;

V(t) is non-stationary input signal goes to k-th neuron.

Nonlinear oscillator neuron has its own dynamics and generates pulses in the absence of external signals at Nk > Nck   , because under this condition tanh( N0k 2Nck-) > 0 and accordingly p2 (N0k; Nck ) > 0 ak

• [14] . Mathematical model (1) can also be used to study the collective behavior of ensembles of neurons interconnected synaptic connections X_jk . For this purpose the second and third terms are necessary to replace N

Xk ^ X where X . = X_k + £^ X , ; a = 1,2,...,N.

j = 1

Solution to equation (1) with the analytical numerical method and consistent approximation method in the form

X kn ) ( t ) = a kn ) ( t )sin ^ kn )(t )             (2)

where n = 1, 2, 3, …, N is an iteration number;

^ <" ) ( t ) = ^ 0 k t + ^ < n ) ( t )                 (3)

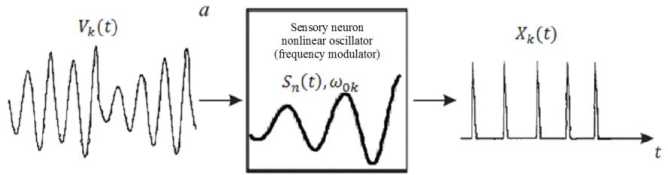
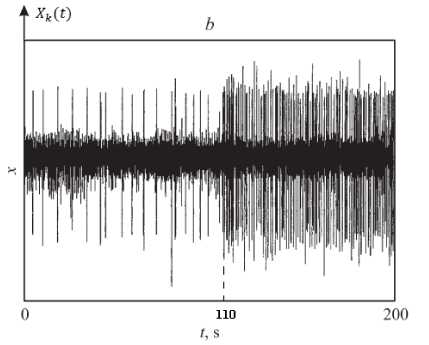
Fig.1. a – Schematic representation of process for the input signal V ( t ) conversion by non-linear oscillator sensory neuron (threshold device). Pulses generating times on the output of threshold device X ( t ) correspond to the crossing moments of the threshold level; b – An experimental sample recording of signal which is generated by biological neurons [13].

a_kⁿ ) ( t ) and ф\ⁿ ) ( t ) - functions of time, which are selected so that the ratio (2) satisfies the equation (1). In addition we impose the condition that a ^{( n )} ( t ) is a slowly variable function, i.e.

lim a kn) ’ ( p k " ) = 1. t ^” a ^{n )(} Pkt )

function. We demand that the condition was fulfilled

X k ⁿ ) = « k 4ⁿ ) ( t ) cos w k ^{n )}( t )           (5)

where X ( ⁿ ) = dX311 , k         _dt

Substituting (2) in (1) and given the condition (5) we obtain the system of equations akn) (t) and Vkn) (t) :

But since there are two functions a(kn) (t) and Vkn) (t), and one equation, this condition ambiguous defines the da" / t) = - akn-1) (t) Pk [(akn-1) )2 sin2 vkn-1) (t)- pk(Nо k; Nek) ] cos2 vkn-1) (t)+Vk(t)cos vkn-1) (t)

dt dv, (t) = ®ok+ Pk [(akn-1) )2 sin2 vkn-1) (t)- pk(Nоk; Nek)] sin vkn-1) (t)cos vkn-1) (t) - Vk (t)8™1Гk-  (t)

The right side of the equation system (6) for the period 2n at V ( t ) = 0 for the rule [15] was averaged:

<Ф>= ^i2" Ф(vkn)) dvkn).(7)

2 n ⁰

In zero approximation expressions for a ⁽⁰⁾ ( t ) and V^Xt ) are found from the system of equations:

da^ = A(ak°4t)), dvk^)(t) = B (a*0)( t))(8)

dtdt

/    (0) 22 where A(ak")(t)) = -a^(t)рАI V-^- — pr I,B(a'k°(.t)) = «оk•

I 82

Integrating the equation (8), a zero approximation expressions for a(0) (t) and Vk^ (t) were worked out:

ak0)( t) =  ■  2 P\   ,(9)

V1 + e"^{Pk P kt}

Vk'(t) = «0 kt(10)

where a ⁽⁰⁾ ( t ) satisfies the criterion (4) of slowly variable function. To find expressions a ⁽¹⁾( t ) and Vk 1 (t ) in the first approximation ( n = 1) we should substitute the expression (9), (10) into the system of equations (6). As a result of integrating we obtain first approximation expressions for a ⁽¹⁾( t ) and ^(t ) . The process of iteration stops when the conditions are fulfilled:

to the operator activation f (fig.2). For nonlinear oscillator sensory neuron activation operator f looks like, this input operator fa = £ + ^k [X'k - P2(N0к; Nck)] d + -. (14) dt2 dt g^( t) - ak f t) ak(n)(t)

<< 1,

vnt ) v k л t ) v k ⁿ⁾( t )

<< 1.

V. Results

For modeling example, in this problem external non-stationary signal V ( t ) is chosen as a sum of N ordinary non-stationary signals, each of which is centered at the point t = t_L and characterized by system parameters L [16]

N - 1

V k (t ) = Z A     ( t - t L ) + A) k .          (11)

^L = ^L 0

By selecting system parameters L, we can to construct mathematical models of complex non-stationary signal V ( t ), spectral properties of which change over time. The mathematical model of unsteady external signal V ( t ) will reflect the dynamics of the real signal that characterizes a physical (biological) process.

An example of a simple non-stationary signal v_Lк (t - t_L ) is an expression:

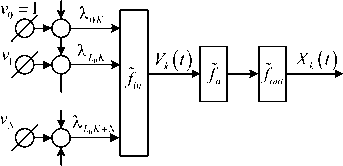
Fig.2. The structure of artificial nonlinear oscillator neuron

v Lk ⁽ t - t L ) = ---- -exp

—

( t ^- t L ) 2 T

cos( ^ ( t - t_L ) + a ),

The output signal of nonlinear oscillator neuron X ( t ) (Fig.2) is transformed by the source operator f the output signal of service activation. Output operator f is required to represent the state of the neuron in the desired field values. In most studies, this operator is not isolated, and under output signal the neuron to understand the signal after activation operator f . However, during the analysis and synthesis of artificial neural networks (ANN), which have different activation functions of the various regions and areas of value determination, is necessary taking into account the output operator. Consequently, nonlinear operator transformation of input signals V ( t ) vector in the vector output signal X ( t ) can be written as

X k ( t ) = L ( f a ( L (V k (t ), A ))).         (15)

which is a product of the envelope Hauss form to oscillating function and is described by five parameters L

^{L  ( A} Lk , ^ L , t L , ^T L ^a L )             ⁽¹³⁾

By selecting different combinations of

L = (A^ ,^, tT ,t ,a ), we can construct a theoretical Lk L L L L model that adequately describes the real physical (biological) processes in the interaction of external non-stationary signal V(t) with its own dynamic physical (biological) nonlinear neuron.

where Ak denotes weight connections of inputs v 1 ,^, v _N of the k -th neuron; Ak is weight shift signal of communication with the k -th neuron; ^ = 2 nf_L is external carrier frequency oscillation in hertz (Hz), t is center localization signal by the time in seconds, t_l is typical localization signal time interval in seconds, a is the initial phase in radians.

Equation (11) with (12) describes all inputs, including offset signal, coming with weights Ak the adder k -th neuron (incoming operator f ). Input operator f converts weighted weights A inputs and presents them

• VI.    Discussion

Figs. 3-4 shows a first term (N = 1) non-stationary external signal V ( t ) ((11), (12)) depending on the time

ALk vl (tt-tL ) =----h^exp

^{L 0} k     L ⁰     2 т _ол/ П

—

⁽ t ^- t i p ⁾² 4r 2

L ₀

^cos( ^ L ₀ ⁽ t ^- t L ) ^{+ a} L ),

applied to nonlinear oscillator sensory neuron for two parameter values Lo: Lo = (3, 4 П, 12, 3, 0); Lo = (1, 6n, 21, 1, 0) in accordance. In the first case the signal v^o^(t - tLo) (Fig.3) has an amplitude Aok = 3, and the second – λ = 1 respectively, in the first case, the signal the initial phase α =0, and the second – f =3Hz; has a frequency f = 2Hz, centered at a point in time t =21s, τ =3s; α =0.

t =12s with time-lapse localization signal τ =3s and

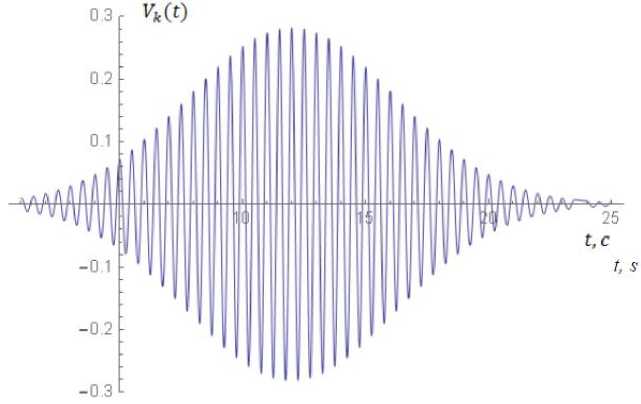
Fig.3. Morphology of the external information signal v ( t - t ) (16) with parameter values L = (3, 4 π , 12, 3, 0); p = 0.4 and µ = 0.1 .

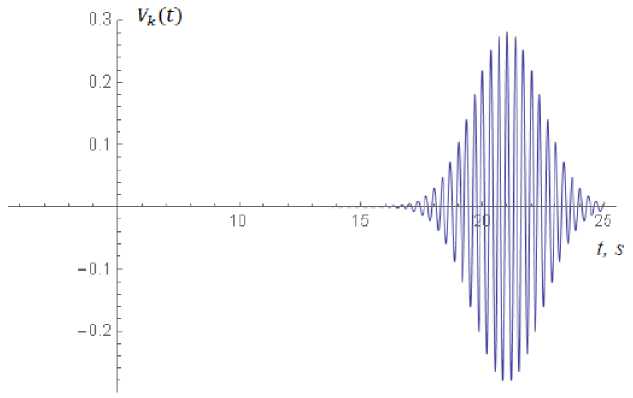
Fig.4. Morphology of the external information signal v ( t - t ) (16) with parameter values L 0 = (1, 6 π , 21, 1, 0); p k =0.4 and µ = 0.1 .

In numerical calculations, signals X ( t ) the output of the nonlinear oscillator neuron with input signals (Figs. 34) parameters p = 0.4 and µ = 0.1 match.

Figs. 5-6 present graphs of frequency modulation dψ(n) (t)

ω(n) = k      , which changes the instantaneous k        dt

(11), which consists of a simple non-stationary signal v ( t - t ) (16), in accordance with a change in signal caused by the interaction of an external signal carrying information with its own dynamics ω = 0.2 π (Fig. 5) and ω = 2 (Fig. 6) nonlinear oscillator neuron.

frequency of the carrier oscillation information V ( t )

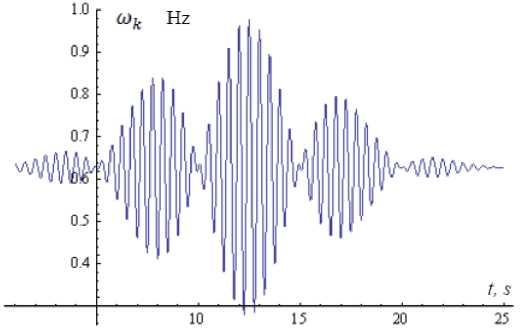
Fig.5. The time dependence of the instantaneous frequency of the carrier signal information v^(tt - t_L ) (16) with parameter values L_o = (3, 4 n , 12, 3, 0); p_k = 0.4 and ^ = 0.1 , ш_ок = 0.2 n .

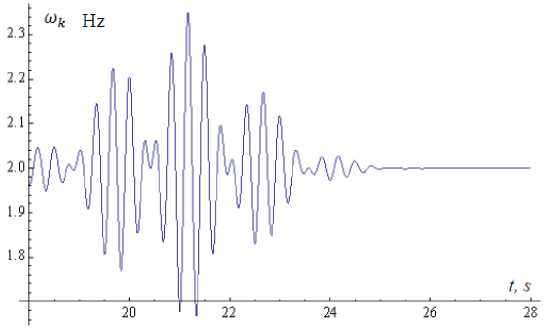
Fig.6. The time dependence of the instantaneous frequency of the carrier signal information v^ _t( t - t_L ) (16) with parameter values L 0 = (1, 6 n ,21,1,0) ; p_k = 0.4 and p _k = 0.1 , ® _{0 k} = 2

Figs. 7-8 present graphs of morphology signal at the output of the nonlinear oscillator neuron X(t) defined by the nature of the interaction of dynamics neuron with frequencies юйк = 0.2n; <УМ = 2 and dynamic, caused by external influence v, , (t -t, ) (16).

L ₀ k       L ₀

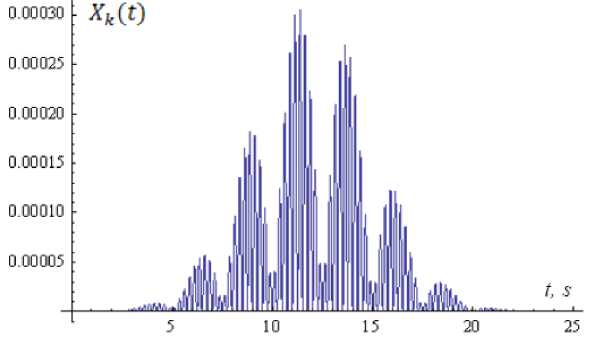
Fig.7. Schedule of morphology signal at the output of the nonlinear oscillator neuron X ( t ) with parameter values

L _o = (3, 4 n , 12, 3, 0); p_k = 0.4 and ^ = 0.1 , ^_k = 0.2 n .

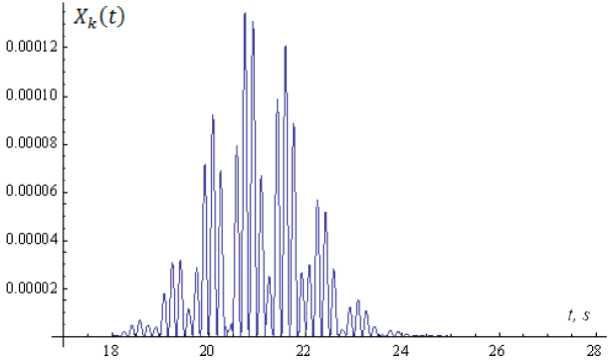
Fig.8. Schedule of morphology signal at the output of the nonlinear oscillator neuron X ( t ) with parameter values

L 0 = (1, 6 п , 21,1,0) ; p_k = 0.4 and ц _к = 0.1 , ® _{0 k} = 2 .

Figs. 9-10 present graphs of morphology signal at the output of the nonlinear oscillator neuron X(t), defined by the nature of the interaction of dynamics neuron with frequencies юйк = 0.2n; <УМ = 2 and dynamic, caused by external influence v, , (t -t, ) (16).

L ₀ k       L ₀

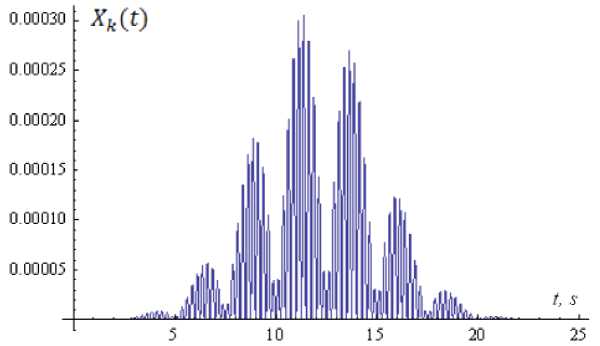
Fig.9. Schedule of morphology signal at the output of the nonlinear oscillator neuron X ( t ) with parameter values

L = (3, 4 n , 12, 3, 0); p_k = 0.4 and ^ = 0.1 , to_ok = 0.2 n .

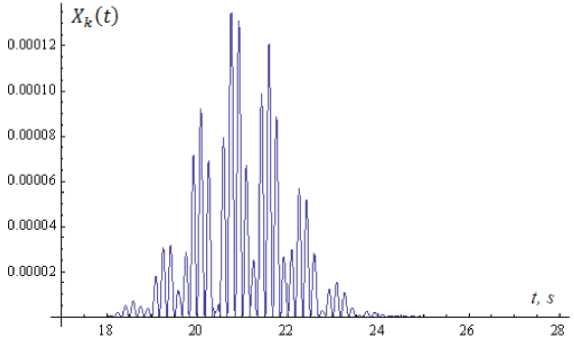
Fig.10. Schedule of morphology signal at the output of the nonlinear oscillator neuron X ( t ) with parameter values

L ₀ = (1, 6 n , 21,1,0) ; p_k = 0.4 and ц _к = 0.1 , ® _{0 k} = 2 .

The interaction of external signal v (t - t ) with parameters L = (3, 4 π , 12, 3, 0); L = (1, 6π, 21, 1, 0) with its own dynamics of nonlinear oscillator neuron ω= 4π or ω= 6π a sharp increase in the amplitude of the output signal X(t) (Fig. 11) compared to the output signal in Fig.9. That is a resonance effect in the external signal frequency which matches the natural frequency of oscillation of the nonlinear neuron, (ω= ω). Graph of modulation frequency ω(n) (t) if a resonance effect is shown in Fig.12.

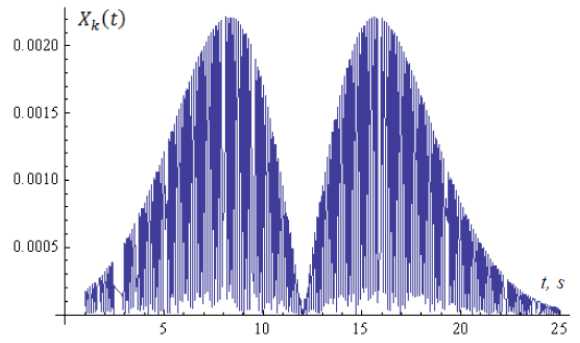
Fig.11. Schedule of morphology signal at the output of the nonlinear oscillator neuron X ( t ) if a resonance effect with parameter values L = (3, 4 π , 12, 3, 0); p = 0.4 and µ = 0.1 , ω = 4 π .

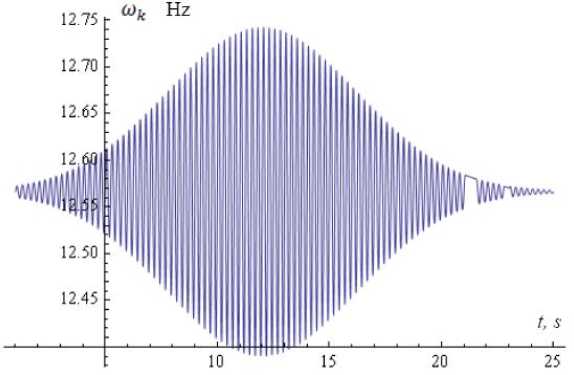
Fig.12. The time dependence of the instantaneous frequency of the carrier signal information v ( t - t ) (16) if a resonance effect with parameter values L = (3, 4 π , 12, 3, 0); p = 0.4 and µ = 0.1 , ω = 4 π .

To decode the structure of output signal X ( t ) , it is important to know the code of program, which describes the inverse operator acting on a vector output, i.e.

f in ^{- 1}( f a ^{- 1}( f o ^- u ¹ t X k ( t ))) = V k ( t , λ Lk ). (17)

Thus, the received results allow hypothesizing that the process of encoding information of nonlinear neurons can be considered in terms of modulation frequency as we know in radio physics that modulation frequency is one way of information transmitting.

• VII.    Conclusions

The method of inhomogeneous nonlinear differential equations with quadratic non linearity of the unknown function at the first derivative was suggested.

It was defined that nonlinear oscillator neuron can act as a frequency modulator, which can modulate the input information of non-stationary signal.

It was determined that nonlinear oscillator neuron with threshold effect significantly alters the structure of the input information non-stationary signal different in shape, frequency and amplitude.

The existence of resonance effects in nonlinear oscillator neuron when frequency of the external non-stationary signal and dynamics of the natural frequency of the neuron are equal is determined.

Information coding with nonlinear oscillator neuron on the basis of frequency modulation and decoding using an inverse operator, which acts on the output signal vector were suggested.