Типизация лесоэксплуатационных условий центральных лесничеств Республики Карелия, Архангельской и Мурманской областей

Автор: Будник Павел Владимирович, Баклагин Вячеслав Николаевич, Галактионов Олег Николаевич

Журнал: Resources and Technology @rt-petrsu

Статья в выпуске: 3 т.21, 2024 года.

Бесплатный доступ

Повышение эффективности лесного хозяйства и лесопользования требует решения вопросов районирования лесных территорий. Цель данного исследования состояла в статистическом обосновании схемы типизации лесоэксплуатационных условий на уровне центральных лесничеств Республики Карелия, Мурманской и Архангельской областей. Лесоэксплуатационное районирование проведено с учётом 19 переменных, характеризующих ресурсы древесины, природно-производственные условия и дорожную инфраструктуру. Источниками данных являлись лесные планы и лесохозяйственные регламенты центральных лесничеств. Методика исследования включала последовательное применение факторного, кластерного и дискриминантного анализов. Факторный анализ применён для устранения мультиколлинеарности и сокращения числа переменных. Извлечение факторов осуществлялось методом максимального правдоподобия, а их количество определялось по критерию Кайзера. Факторная структура подвергалась вращению методом Варимакс. В результате факторного анализа выделено 4 фактора, которые объясняют 83,16 % общей дисперсии 19 переменных. Первый фактор определял общую продуктивность лесов и уровень расчётной лесосеки по хвойному хозяйству. Второй фактор характеризовал уровень лиственного хозяйства и природно-производственные условия, характерные для лесов с высоким содержанием лиственных пород. Третий фактор характеризовал объём расчётной лесосеки по сплошным рубкам. Четвёртый фактор определял степень соответствия природно-производственных условий благоприятным условиям (более сухие почвы и продуктивные леса). Кластерный анализ включал два этапа. На первом этапе применён иерархический кластерный анализ с целью определения числа кластеров. На втором этапе использован метод k-средних для деления центральных лесничеств на заданное количество групп. По итогам кластерного анализа исследуемый регион разделён на 9 лесоэксплуатационных районов и разработана карта-схема. Достоверность результатов кластерного анализа подтверждена статистическими критериями дискриминантного анализа: значениями канонической корреляции, критерием χ^2 Пирсона, критерием лямбда Уилкса.

Еще

Районирование, факторный анализ, кластерный анализ, метод k-средних, дискриминантный анализ, лесозаготовки, управление лесами

Короткий адрес: https://sciup.org/147244384

IDR: 147244384 | DOI: 10.15393/j2.art.2024.7983

Текст научной статьи Типизация лесоэксплуатационных условий центральных лесничеств Республики Карелия, Архангельской и Мурманской областей

Для целей учёта вариативности природно-производственных условий лесных территорий при принятии мер, направленных на организацию лесного хозяйства и лесопользования, требуется комплексное лесоэксплуатационное районирование, основанное на научно обоснованных подходах [1]. Районирование предполагает группировку лесных территорий со сходными особенностями, т. е. их типизацию. Это позволяет эффективно планировать мероприятия по освоению ресурсов древесины, включая её заготовку и переработку, а также обеспечить сохранение биоразнообразия и продуктивности лесных территорий. Типизация лесоэксплуатационных условий позволяет реализовать системный подход в сфере управления лесной отраслью. Регион как объект стратегического управления рассматривается как система, состоящая из подсистем, представляющих собой группы более мелких территорий со своими особенностями. Принятие во внимание этих особенностей, а также других характеристик групп и их потенциала позволяет вырабатывать программные подходы к стратегическому планированию развития как отдельных подсистем, так и системы (региона) в целом.

В последнее время для решения вопросов группировки и классификации антропогенных объектов и объектов геопространства широко применяются методы многомерного статистического анализа, в частности, факторный и кластерный анализы [2—5]. Это позволяет повысить научную обоснованность и достоверность получаемых результатов. С применением подобного подхода отечественными специалистами предложены классификация лесных территорий Центрального федерального округа [6], Приволжского федерального округа [7], Северо-Западного федерального округа [8], Нижегородской области [1], Вологодской области [9], Свердловской области [10] и др.

Одним из сложных вопросов при районировании лесных территорий является проблема обоснования комплекса показателей, с использованием которого осуществляется многомерный статистический анализ. В отличие от вышеотмеченных работ в контексте данного исследования лесные территории рассматриваются с точки зрения лесоэксплуатации. Поэтому выбор показателей для районирования обоснован, прежде всего, их влиянием на экономическое освоение лесных ресурсов, а именно на лесозаготовки. В работах [11], [12] отмечается, что эффективность лесозаготовительных компаний в России определяется объёмом доступной древесины, производственными мощностями, а также спросом на продукцию.

Объём доступной древесины может быть охарактеризован расчётной лесосекой. При этом, учитывая отличающуюся экономическую ценность различных пород древесины, целесообразно рассматривать расчётную лесосеку раздельно по хвойным и лиственным породам. Многими исследованиями доказано влияние вида рубок на производительность лесозаготовительных машин [13—15]. Поэтому необходимо учитывать долю расчётной лесосеки, приходящейся на тот или иной вид рубок.

Размеры центральных лесничеств достаточно сильно варьируются и параметры расчётной лесосеки не в полной мере могут охарактеризовать ресурсный потенциал лесной территории. По нашему мнению, в качестве дополнительной характеристики можно взять отношение расчётной лесосеки к общему запасу древесины.

На практике не весь имеющийся запас древесины может быть освоен по экономическим причинам, что в значительной степени определяется логистическими проблемами. Известно, что значительную долю операционных затрат на заготовку древесины составляет транспорт [16], [17]. Поэтому при типизации лесных территорий необходимо учитывать транспортную доступность ресурсов древесины и их распределённость по территории. В данном исследовании предложено использовать показатели лесистости и плотности дорог.

Производственная мощность определяется не только количественными и качественными показателями средств производства, но и условиями их работы. Многими исследованиями доказано влияние среднего объёма древесины на гектаре, а также породного состава [23—25] на производительность харвестера [18], [19] и форвардера [20—22]. Поэтому целесообразно при типизации лесных территорий учитывать показатели средних запасов древесины по породам и бонитетам. Кроме того, эффективность лесозаготовительных машин определяется почвенно-грунтовыми условиями [21], [26] и другими природно-производственными факторами. В работе [27] в качестве косвенной оценки, характеризующей природно-производственные условия, нами предложено использовать распределение земель лесного фонда по классам природной пожарной опасности лесов в сопоставлении с классификацией типов леса академика В. Н. Сукачёва [28]. Подобный подход также был реализован в этом исследовании.

Цель данного исследования состоит в статистическом обосновании схемы типизации лесоэксплуатационных условий на уровне центральных лесничеств регионов России на побережье Белого моря, а именно Республики Карелия, Мурманской и Архангельской областей. Выбор региона исследования обосновывается, в первую очередь, возрастанием геоэкономического значения северных территорий и, в частности, Арктической зоны [29], [30], а также важностью лесопромышленных комплексов регионов в их структуре экономики.

2. Материалы и методы

В таблице 1 представлены некоторые описательные статистики переменных, учитываемых в исследовании. Источниками данных являлись документы лесного планирования субъектов (лесные планы) и лесохозяйственные регламенты соответствующих центральных лесничеств.

Методика типизации на уровне центральных лесничеств состояла в последовательном применении факторного [31], кластерного [32] и дискриминантного [33] анализов. Целью применения факторного анализа являлось устранение мультиколлинеарности и сокращение числа переменных для кластерного анализа. Для извлечения факторов использовался метод максимального правдоподобия [34], а их количество определялось по критерию Кайзера [35].

Таблица 1. Описательные статистики переменных, характеризующих центральные лесничества региона исследования

Table 1. Descriptive statistics of variables characterizing the central forest districts of the study region

О co о о Ю o О и	Описание переменной	u и	U °
S_II	Доля территории лесничества, приходящаяся на 2-й класс пожарной опасности	0,07	0,05
S_III	Доля территории лесничества, приходящаяся на 3-й класс пожарной опасности	0,13	0,09
S_IV	Доля территории лесничества, приходящаяся на 4-й класс пожарной опасности	0,32	0,13
S_V	Доля территории лесничества, приходящаяся на 5-й класс пожарной опасности	0,34	0,15
Rd_cover	Отношение расчётной лесосека для осуществления сплошных рубок спелых и перестойных лесных насаждений в эксплуатационных лесах к расчётной лесосеке при всех видах рубок по лиственному хозяйству (в ликвидном объёме)	0,53	0,31
Rc_cover	Отношение расчётной лесосека для осуществления сплошных рубок спелых и перестойных лесных насаждений в эксплуатационных лесах к расчётной лесосеке при всех видах рубок по хвойному хозяйству (в ликвидном объёме)	0,61	0,29
Se_f	Отношение площади эксплуатационных лесов к площади всех лесов	0,62	0,28
L	Отношение площади, покрытой лесной растительностью, к общей площади лесничества (лесистость)	0,73	0,15
P	Плотность дорог, км/тыс. га	2,25	1,27
Rd_v	Отношение расчётной лесосеки при всех видах рубок по лиственному хозяйству (в ликвидном объёме) к запасу древесины на землях лесного фонда (‰)	2,86	3,29
Rc_v	Отношение расчётной лесосеки при всех видах рубок по хвойному хозяйству (в ликвидном объёме) к запасу древесины на землях лесного фонда (‰)	7,04	3,92
Vp_IV—V	Средний запас на гектар сосны IV—V классов бонитета в эксплуатационном фонде для сплошных рубок, м³	104,32	44,45
Vs_b	Средний запас на гектар берёзы в эксплуатационном фонде для сплошных рубок, м³	124,23	62,18
Vs_IV—V	Средний запас на гектар ели IV—V классов бонитета в эксплуатационном фонде для сплошных рубок, м³	126,82	61,32
Vs_a	Средний запас на гектар осины в эксплуатационном фонде для сплошных рубок, м³	143,41	104,69
Vp_I—III	Средний запас на гектар сосны I—III классов бонитета в эксплуатационном фонде для сплошных рубок, м³	163,62	97,45
Vs_I—III	Средний запас на гектар ели I—III классов бонитета в эксплуатационном фонде для сплошных рубок, м³	172,21	121,25
Rd	Расчётная лесосека по лиственному хозяйству, тыс. м³	229,1	314,22
Rc	Расчётная лесосека по хвойному хозяйству, тыс. м³	501,14	423,96

Для минимизации количества переменных, которые имеют высокие нагрузки на каждый фактор, был применён метод Варимакс [36]. Перечень переменных, участвующих в факторном анализе, осуществлялся на основе анализа корреляционной матрицы. Контроль применимости факторного анализа к данным проводился по критерию адекватности выборки Кайзера — Мейера — Олкина (КМО) [37] и критерию сферичности Бартлетта [38].

Кластерный анализ с применением z-оценок собственных значений факторов и отдельных переменных, не использованных в факторном анализе, осуществлялся в два этапа. На первом этапе проводился иерархический кластерный анализ, целью которого было выявление оптимального количества кластеров [39]. Для построения дендрограмм использовались метод средней связи, метод связи внутри группы, центродидный метод, а также метод Уорда. При этом там, где это было возможно, применялись различные метрики: евклидово расстояние, квадрат евклидова расстояния, расстояние Чебышева. На втором этапе использовался метод k-средних [40]. Для создания карты-схемы применялось разработанное авторами veb-приложение информационно-аналитической системы, интерфейс которой реализован на встраиваемом языке программирования javascript, где для непосредственной визуализации картографической информации применяется библиотека leaflet с открытым исходным кодом (javascript).

Дискриминантный анализ использовался для целей проверки результатов кластерного анализа. Статистическая значимость дискриминантных фикций, различающих группы переменных, осуществлялась по критерию / ² Пирсона. Различия средних значений дискриминантных функций оценивалось по лямбде Уилкса. Взаимосвязь между расчётными значениями дискриминантных функций и принадлежности лесничества к кластеру оценивалась по коэффициентам канонической корреляции.

3. Результаты 3.1. Результаты факторного анализа

Анализ корреляционной матрицы потребовал исключить переменную P из факторного анализа, т. к. она слабо коррелировала с другими переменными, участвующими в исследовании. В отношении оставшихся переменных величина КМО составила 0.788. Критерий сферичности Бартлетта показал значимое отличие от 0 корреляции между переменными (p < 0.001). В соответствии с критерием Кайзера выделено 4 фактора (рисунок 1), которые объясняли 83,16 % общей дисперсии переменных (таблица 2). Анализ общностей переменных не дал оснований для необходимости исключить из анализа какую-либо переменную (таблица 3).

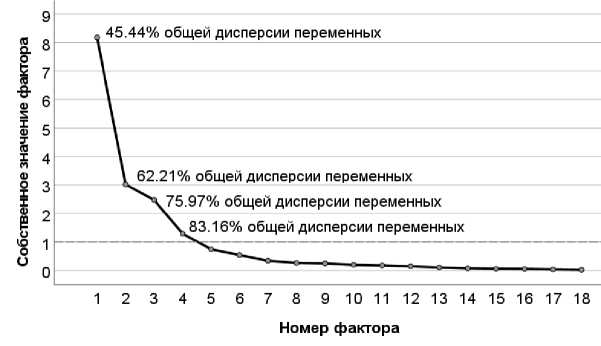
Рисунок 1. График собственных значений выделяемых факторов [рисунок авторов]

Figure 1. Graph of the eigenvalues of the selected factors

Таблица 2. Характеристика факторов

Table 2. Characteristics of factors

№ фактора	Собственное значение	Доля дисперсии переменных, объясняемая факторами, %	Суммарная доля объясняемой дисперсии переменных, %
1	8,18	45,44	45,44
2	3,02	16,78	62,21
3	2,48	13,75	75,97
4	1,30	7,19	83,16

Таблица 3. Значения общностей переменных при выделении факторов методом максимального правдоподобия

Table 3. Community values of variables when identifying factors using the maximum likelihood method

Обозначение переменной	Общность	Обозначение переменной	Общность
Se_f	0,927	Vs_a	0,797
Vp_I—III	0,920	S_III	0,795
Vs_b	0,909	Rd_v	0,788
Vp_IV—V	0,899	Vs_I—III	0,750
Rc_cover	0,891	Rc_v	0,689
S_V	0,883	Rd	0,674
S_IV	0,857	Rd_cover	0,670
S_II	0,839	L	0,647
Vs_IV—V	0,834	Rc	0,396

В таблице 4 приведена структура факторных нагрузок. В формировании фактора № 1 (F1) участвуют переменные, характеризующие средние запасы леса по породам и расчётную лесосеку по хвойному хозяйству. Фактор № 2 (F2) включает переменные, характеризующие лиственные хозяйства и природно-производственные условия, характерные для лесов с высоким содержанием лиственных пород. Фактор № 3 (F3) сформирован переменными, характеризующими расчётную лесосеку по сплошным рубкам. В формировании фактора № 4 (F4) участвуют переменные, характеризующие степень соответствия природно-производственных условий благоприятным условиям по меркам исследуемого региона.

Таблица 4. Факторные нагрузки при выделении четырёх факторов после вращения системы координат

Table 4. Factor loadings when identifying four factors after rotating the coordinate system

Обозначение переменной	Факторная нагрузка по номерам факторов
Обозначение переменной	1	2	3	4
Vp_I—III	0,902	0,252	0,156	–0,135
Vs_IV—V	0,866	0,041	0,366	0,112
Vs_b	0,794	0,462	0,255	0,016
Rc_v	0,769	–0,049	0,078	0,297
Vs_IV—V	0,755	0,329	0,394	–0,034
Vs_I—III	0,687	0,460	0,216	–0,145
Rc	0,506	0,162	0,285	–0,181
S_IV	–0,104	0,915	–0,021	–0,094
Rd_v	0,275	0,842	0,062	0,004
Rd	0,217	0,779	0,110	–0,088
L	0,258	0,731	0,074	0,202
Vs_a	0,517	0,659	0,199	–0,237
Rc_cover	0,219	0,142	0,894	–0,154
Se_f	0,381	0,290	0,819	–0,166
Rd_cover	0,344	–0,165	0,723	0,031
S_V	0,105	–0,319	0,035	–0,877
S_III	0,274	–0,160	–0,275	0,786
S_II	–0,193	–0,533	0,017	0,720

3.2. Результаты кластерного анализа

Анализ дендрограмм показал, что целесообразно в регионе исследования выделить 9 кластеров. В таблице 5 приведены результаты кластерного анализа методом k-средних. Карта-схема кластеров представлена на рисунке 2.

Таблица 5. Результаты кластеризации методом k-средних

Table 5. K-means clustering results

№	Лесничество	О И о ctf £	Расстояние до центра	№	Лесничество	Ри О И о ей £	Расстояние до центра
1	Кировское	1	1,990	29	Муезерское	3	0,765
2	Ловозерское	1	1,565	30	Сегежское	3	0,428
3	Мончегорск	1	0,968	31	Кондопожское	3	1,613
4	Мурманское	1	1,154	32	Мезенское	4	0,000
5	Терское	1	0,735	33	Зашейковское	5	0,728
6	Архангельское	1	1,807	34	Кандалакшское	5	0,960
7	Березниковское	2	0,399	35	Ковдозерское	5	1,204
8	Выйское	2	0,549	36	Кольское	5	1,918
9	Емецкое	2	0,654	37	Печенгское	5	1,169
10	Каргопольское	2	0,936	38	Питкярантское	6	0,000
11	Карпогорское	2	0,550	39	Сортавальское	7	1,382
12	Красноборское	2	0,740	40	Олонецкое	7	1,240
13	Лешуконское	2	1,163	41	Лахденпохское	7	1,430
14	Онежское	2	0,880	42	Пудожское	8	0,954
15	Пинежское	2	0,647	43	Пряжинское	8	1,386
16	Приозёрное	2	0,981	44	Прионежское	8	1,268
17	Пуксоозерское	2	1,153	45	Вельское	8	0,703
18	Северодвинское	2	1,390	46	Верхнетоемское	8	0,894
19	Сурское	2	1,571	47	Вилегодское	8	0,578
20	Холмогорское	2	0,749	48	Коношское	8	1,510
21	Шенкурское	2	1,030	49	Котласское	8	0,986
22	Кемское	3	1,615	50	Няндомское	8	0,777
23	Лоухское	3	0,762	51	Обозерское	8	1,032
24	Беломорское	3	0,929	52	Плесецкое	8	0,673
25	Калевальское	3	1,014	53	Устьянское	8	1,217
26	Суоярвское	3	1,033	54	Яренское	8	1,148
27	Медвежьегорское	3	0,960	55	Сийское	9	0,330
28	Костомукшское	3	1,030	56	Соловецкое	9	0,330

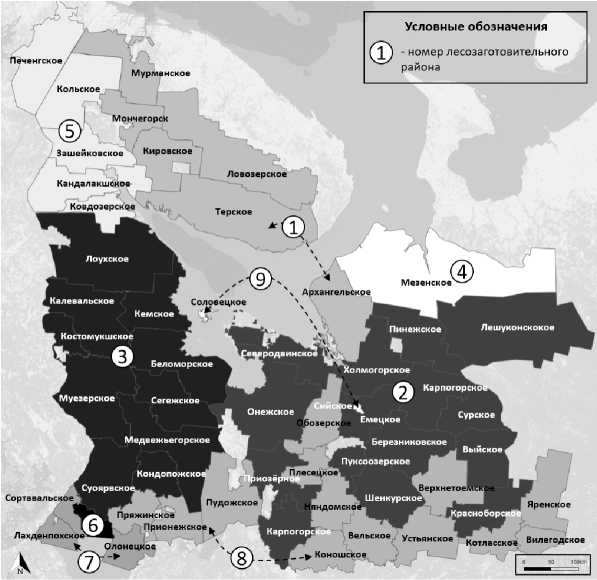
Рисунок 2. Карта-схема лесоэксплуатационных районов Республики Карелия, Мурманской и Архангельской областей [рисунок авторов]

Figure 2. A schematic map of the forest exploitation areas of the Republic of Karelia, Murmansk and Arkhangelsk regions

Анализ средних значений факторов показал, что кластеры различаются и не дублируют друг друга (рисунок 3). По мере движения с юга на север происходит постепенное оскудение ресурсов древесины, а также снижение запасов лиственных пород в древостоях.

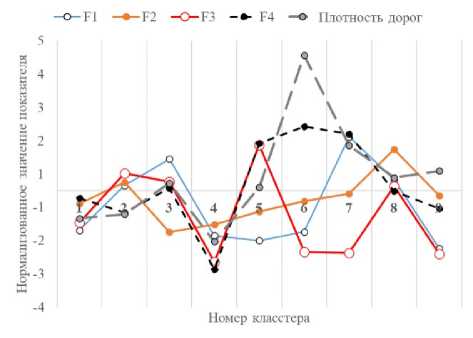
Рисунок 3. График средних значений в кластерах в координатах факторов [рисунок авторов]

Figure 3. Graph of average values in clusters in factor coordinates

В таблицах 6—8 представлены средние значения переменных по кластерам.

Таблица 6. Средние значения переменных, составляющих фактор F1

Table 6. Average values of the variables that make up factor F1

№ кластера	Vp_I—III	Vp_IV—V	Vs_b	Vs_I—III	Vs_IV—V	Rc_v	Rc
1	34	50	47	0	52	1,47	54,25
2	203	109	138	268	153	7,58	765,40
3	146	146	137	167	150	9,83	618,62
4	0	0	0	0	0	0,63	107,20
5	80	80	65	0	74	3,98	84,94
6	0	0	0	0	0	11,98	360,20
7	153	153	184	259	151	13,47	407,73
8	221	122	181	245	167	7,69	611,92
9	0	0	0	0	0	0,16	0,35

Таблица 7. Средние значения переменных, составляющих факторы F2 и F3

Table 7. Average values of the variables that make up factor F2 and F3

№ кластера	S_IV	Rd_v	Rd	L	Vs_a	Se_f	Rc_cover	Rd_cover
1	0,32	0,19	5,48	0,52	44,00	0,22	0,28	0,23
2	0,37	2,73	238,85	0,79	210,40	0,80	0,84	0,60
3	0,13	1,01	75,25	0,60	108,50	0,69	0,66	0,77
4	0,21	0,11	19,40	0,47	0,00	0,00	0,00	0,00
5	0,24	0,21	4,50	0,68	0,00	0,69	0,77	0,73
6	0,20	1,71	51,50	0,90	0,00	0,00	0,00	0,00
7	0,30	2,82	100,17	0,85	138,67	0,19	0,19	0,32
8	0,46	7,41	620,51	0,86	239,23	0,79	0,69	0,54
9	0,35	0,21	0,45	0,73	0,00	0,00	0,00	0,00

Таблица 8. Средние значения плотности дорог и переменных, составляющих фактор F4

Table 8. Average values of road density and variables that make up factor F4

№ кластера	S_V	S_III	S_II	P
1	0,34	0,07	0,10	1,19
2	0,42	0,04	0,08	1,35
3	0,40	0,09	0,17	2,53
4	0,72	0,02	0,02	0,30
5	0,17	0,15	0,16	2,38
6	0,10	0,14	0,35	7,40
7	0,13	0,11	0,33	3,97
8	0,28	0,03	0,11	2,74

3.3. Результаты дискриминантного анализа

С использованием дискриминантного анализа были изучены различия центральных лесничеств и осуществлена их классификация по группам. Для этого было найдено пять канонических дискриминантных функций вида

D _t = a i F1 + b t F2 + C i F3 + d t F4 + f _i P D i = a i F1 + b i F2 + c i F3 + d i F4 + f i P , (1)

где a i , bi , C i , d i , f i — коэффициенты канонической дискриминантной функции, определяемые согласно таблице 9; F1, F2, F3 , F4 — стандартизованные собственные значения факторов, полученных в ходе факторного анализа, P — стандартизованное значение плотности дорог.

Таблица 9. Коэффициенты канонических дискриминантных функций

Table 9. Coefficients of canonical discriminant functions

Переменная дискриминантной функции	№ д искримина нтной функции
Переменная дискриминантной функции	1	2	3	4	5
F1	2,299	1,332	– 0,218	– 0,694	0,182
F2	1,124	– 0,461	– 1,178	1,095	0,308
F3	1,715	– 0,992	1,283	0,460	– 0,381
F4	– 0,272	0,638	1,027	0,355	1,050
P	– 0,340	1,036	0,098	0,907	– 1,045

Таблица 10. Собственные значения, доля объясняемой дисперсии и значения канонической корреляции дискриминантных функций

Table 10. Eigenvalues, proportion of explained variance and canonical correlation values of discriminant functions

№ функции	Собственное значение	Доля дисперсии переменных, объясняемых функцией, %	Суммарная объясняемая дисперсия, %	Каноническая корреляция
1	10,790	46,7	46,7	0,957
2	5,840	25,3	72,0	0,924
3	3,831	16,6	88,5	0,891
4	2,305	10,0	98,5	0,835
5	0,347	1,5	100,0	0,508

Дискриминантные функции в сумме объясняют 100 % дисперсии их переменных (таблица 10). В данном случае в качестве переменных выступали значения факторов, полученные в процессе факторного анализа, и значения плотности дорог. Значения канонической корреляции находились в диапазоне 0,509—0,957. Поэтому можно сделать заключение о действительной разделительной способности полученных дискриминантных функций (см. таблицу 10). Классификация центральных лесничеств прошла успешно, т. к. лямбда Уилкса для первых трёх дискриминантных функций приближалась к 0 и статистически значимыми являлись все пять дискриминантных функций (таблица 11). Достоверность устанавливаемых различий между группами центральных лесничеств, определённых на основе дискриминантных функций, подтвердилась превышением расчётного значения /2 над теоретическим значением /2а6л. хТабл. на 1 %-м уровне значимости (см. таблицу 11).

Таблица 11. Результаты дискриминантного анализа

Table 11. Results of discriminant analysis

Критерий для функций	Лямбда Уилкса	Z ²	Х табл. (при уровне значимости 0,01)	Число степеней свободы	Значимость
От 1 до 5	0,001	358,014	22,164	40	< 0,001
От 2 до 5	0,007	239,585	13,565	28	< 0,001
От 3 до 5	0,046	147,292	7,015	18	< 0,001
От 4 до 5	0,225	71,688	2,558	10	< 0,001
5	0,742	14,311	0,297	4	0,006

Предположение о принадлежности центрального лесничества к классу с использованием дискриминантных функций в 100 % случаев совпало с результатами кластерного анализа. Таким образом, результаты кластерного анализа могут быть признаны статистически значимыми.

4. Обсуждение и заключение

Результаты исследования не претендуют на исчерпывающий характер, а являются альтернативной попыткой классификации лесоэксплуатационных условий в исследуемом регионе. Необходимо учитывать ограниченность результатов исследования. В частности, предложенная типизация лесоэксплуатационных условий центральных лесничеств основана на учёте ограниченного и определённого количества переменных, которые не могут в полном объёме охарактеризовать условия центральных лесничеств с точки зрения качественных и количественных показателей имеющихся ресурсов, природнопроизводственных условий, а также количественных и качественных характеристик инфраструктуры.

Качество исследования могло быть повышено путём учёта дополнительных факторов, в частности, средней температуры, количества осадков, глубины снежного покрова, рельефа, распределения видов почв и стволов по толщине и высоте. Кроме того, для целей исследования было бы полезно учитывать наличие крупных деревообрабатывающих предприятий на территории лесничества, а также иных переменных, характеризующих работу как лесозаготовительных, так и деревообрабатывающих предприятий, которые необходимо учитывать при оптимальном планировании заготовки древесины и её переработки. Например, в качестве таких переменных могли бы выступать оценки следующих факторов, важность которых отмечается в многочисленных работах ([7], [11], [41], 42]): характеристики спроса на продукты заготовки древесины; степень соответствия леса структуре спроса; состояние дорог, стоимость их строительства и расходы на транспортировку; имеющиеся производственные мощности по заготовке и переработке; кадровый потенциал; период времени, в течение которого может быть осуществлена заготовка; показатели лесовосстановления и воспроизводства лесных ресурсов. В то же время сдерживающим фактором в учёте вышеотмеченных характеристик являются отсутствие данных по каждому центральному лесничеству или практическая сложность их сбора и обеспечения их полноты и достоверности. Кроме того, наиболее лучший результат дала бы типизация на уровне участковых лесничеств, а именно на уровне выделов. Однако здесь остро возникает проблема доступности данных. Вместе с тем полученные результаты хорошо согласуются с другими исследованиями, целью которых являлся систематический анализ лесной отрасли России [43], [44].

В данном исследовании на основе методов многомерной статистики предложена карта лесоэксплуатационных районов Республики Карелия, Мурманской и Архангельской областей. Методика включала последовательное применение факторного, кластерного и дискриминантного анализов. Таким образом, в исследуемом регионе 56 центральных лесничеств были разделены на 9 районов. Деление на районы осуществлялось с учётом 19 переменных, характеризующих качественно-количественные характеристики ресурсов древесины, природно-производственные условия и уровень дорожной инфраструктуры.

Факторный анализ показал, что дисперсия переменных, включённых в анализ (исключая значение плотности дорог), может быть объяснена на 83,16 % четырьмя факторами. Первый фактор определяет общую продуктивность лесов и уровень расчётной лесосеки по хвойному хозяйству. Второй фактор характеризует уровень лиственного хозяйства и природнопроизводственные условия, характерные для лесов с высоким содержанием лиственных пород (переувлажнённые почвы). Третий фактор определяет объём расчётной лесосеки по сплошным рубкам. Четвёртый фактор характеризует степень соответствия природнопроизводственных условий благоприятным условиям по меркам исследуемого региона (более сухие почвы и продуктивные леса).

Результаты дискриминантного анализа подтвердили статистическую достоверность деления центральных лесничеств исследуемого региона на 9 районов. Различия между центральными лесничествами, принадлежащими к разным районам, подтверждены по критерию /2 . Данные исследований могут быть учтены при решении вопросов рационального планирования и организации освоения лесосечного фонда, при планировании развития транспортной сети, обоснования применяемых систем лесозаготовительных машин.

Исследование выполнено на средства гранта Российского научного фонда № 23-21-00143,

Список литературы Типизация лесоэксплуатационных условий центральных лесничеств Республики Карелия, Архангельской и Мурманской областей

Хлюстов В. К., Ганихин А. М., Короткая С. В. Ресурсно-экологическое районирование лесов Нижегородской области // Природообустройство. 2021. № 3. С. 128—136. DOI: 10.26897/1997-6011-2021-3-128-136.
Management goals and performance: clustering state forest management organizations in Europe with multivariate statistics / A. Liubachyna, A. Bubbico, L. Secco [et al.] // Forests. 2017. Vol. 8, no. 12. P. 504. DOI: doi.org/10.3390/f8120504.
Mapping the causes of forest fires in portugal by clustering analysis / A. C. Meira Castro, A. Nunes, A. Sousa [et al.] // Geosciences. 2020. Vol. 10, no. 2. P. 53. DOI: doi.org/10.3390/-geosciences10020053.
Tutmez B., Ozdogan M. G., Boran A. Mapping forest fires by nonparametric clustering analysis // Journal of forestry research. 2018. Vol. 29. P. 177—185. DOI: doi.org/10.1007/-s11676-017-0417-4.
Parente J., Pereira M. G., Tonini M. Space-time clustering analysis of wildfires: The influence of dataset characteristics, fire prevention policy decisions, weather and climate // Science of the total environment. 2016. Vol. 559. P. 151—165. DOI: doi.org/10.1016/j.scitotenv.2016.03.129.
Хлюстов В. К., Васенев И. И., Ганихин А. М. Районирование территории ЦФО по комплексу лесоводственно-климатических показателей // АгроЭкоИнфо. 2020. № 2. С. 16—16. URL: https://agroecoinfo.narod.ru/journal/STATYI/2020/2/st_206.pdf. Текст: электронный.
Multidimensional modeling of the economy of forest management and reforestation / G. Salimova, A. Ableeva, T. Lubova // Ecological Modelling. 2022. Vol. 472. P. 110098. DOI: doi.org/10.1016/j.ecolmodel.2022.110098.
Хлюстов В. К. Комплексная оценка и управление древесными ресурсами: модели — нормативы — технологии. М.: РГАУ-МСХА им. К. А. Тимирязева, 2015. Кн. I. 389 с.
Ворошилов Н. В. Развитие лесного комплекса в муниципалитетах региона (на материалах Вологодской области) // Вопросы территориального развития. 2020. Т. 8, № 5. С. 4. DOI: 10.15838/tdi.2020.5.55.4.
Годовалов Г. А., Залесов С. В., Лежнина Е. Н. Районирование лесов Свердловской области // Аграрный вестник Урала. 2011. № 8. С. 38—39. URL: https://cyberleninka.ru/article/n/-rayonirovanie-lesov-sverdlovskoy-oblasti. Текст: электронный.
Optimal planning of wood harvesting and timber supply in Russian conditions / A. Shabaev, A. Sokolov, A. Urban [et al.] // Forests. 2020. Vol. 11, no. 6. P. 662. DOI: doi.org/10.3390/-f11060662.
Improving Cut-to-length Operations Management in Russian Logging Companies Using a New Decision Support System / Yu. Yu. Gerasimov, A. P. Sokolov, D. Fjeld // Baltic Forestry. 2013. Vol. 19, no. 1. P. 36. URL: https://www.cabidigitallibrary.org/doi/full/10.5555/20133363677. Text. Image: electronic.
Spinelli R., Magagnotti N. The effect of harvest tree distribution on harvesting productivity in selection cuts // Scandinavian Journal of Forest Research. 2013. Vol. 28, no. 7. P. 701 —709. DOI: doi.org/10.1080/02827581.2013.821517.
Lageson H. Effects of thinning type on the harvester productivity and on the residual stand // Journal of Forest Engineering. 1997. Vol. 8, no. 2. P. 7—14. URL: https://www.tandfonline.-com/doi/abs/10.1080/08435243.1997.10702699. Text. Image: electronic.
Comparison of single-grip harvester productivity in clear-and shelterwood cutting / L. Eliasson, J. Bengtsson, J. Cedergren [et al.] // Journal of Forest Engineering. 1999. Vol. 10, no. 1. P. 43—48. URL: https://www.tandfonline.com/doi/abs/10.1080/08435243.1999.10702723. Text. Image: electronic.
A mathematical modeling for simultaneous routing and scheduling of logging trucks in the forest supply chain / L. Melchiori, G. Nasini, J. M. Montagna [et al.] // Forest Policy and Economics. 2022. Vol. 136. P. 102693. DOI: doi.org/10.1016/j.forpol.2022.102693.
Mokhirev A., Medvedev S. Assessment of road density in logging areas using geographical information systems // IOP Conference Series: Earth and Environmental Science. IOP Publishing, 2020. Vol. 507, no. 1. P. 012022. DOI: 10.1088/1755-1315/507/1/012022.
Kormanek M., Baj D. Analysis of operation performance in the process of machine wood harvesting with Fao Far 6840 mini-harvester // Agricultural engineering. 2018. Vol. 22, no. 1. P. 73—82. DOI: 10.1515/agriceng-2018-0007.
Kärhä K., Rönkkö E., Gumse S. I. Productivity and cutting costs of thinning harvesters // International Journal of Forest Engineering. 2004. Vol. 15, no. 2. P. 43—56. DOI: doi.org/-10.1080/14942119.2004.10702496.
Kellogg L. D., Bettinger P. Thinning productivity and cost for a mechanized cut-to-length system in the Northwest Pacific Coast region of the USA // Journal of Forest Engineering. 1994. Vol. 5, no. 2. P. 43—54. DOI: doi.org/10.1080/08435243.1994.10702659.
Factors affecting forwarder productivity / A. R. Proto, G. Macrì, R. Visser [et al.] // European Journal of Forest Research. 2018. Vol. 137. P. 143—151. DOI: doi.org/10.1007/s10342-017-1088-6.
Factors affecting operational cost and productivity of ground-based timber harvesting machines: a meta-analysis / L. T. Louis, A. R. Kizha, A. Daigneault [et al.] // Current Forestry Reports. 2022. Vol. 8, no. 1. P. 38—54. DOI: doi.org/10.1007/s40725-021-00156-5.
Automatic GNSS-enabled harvester data collection as a tool to evaluate factors affecting harvester productivity in a Eucalyptus spp. harvesting operation in Uruguay / A. Olivera, R. Visser, M. Acuna [et al.] // International journal of forest engineering. 2016. Vol. 27, no. 1. P. 15—28. DOI: doi.org/10.1080/14942119.2015.1099775.
Hiesl P., Benjamin J. G. Applicability of international harvesting equipment productivity studies in Maine, USA: A literature review // Forests. 2013. Vol. 4, no. 4. P. 898—921. DOI: doi.org/-10.3390/f4040898.
Effect of tree form on the productivity of a cut-to-length harvester in a hardwood dominated stand / E. R. Labelle, M. Soucy, A. Cyr [et al.] // Croatian Journal of Forest Engineering: Journal for Theory and Application of Forestry Engineering. 2016. Vol. 37, no. 1. P. 175—183. URL: https://hrcak.srce.hr/153483. Text. Image: electronic.
Economic feasibility of timber harvesting in lowlands / A. K. George, A. R. Kizha, L. Kenefic [et al.] // Exceeding the vision: forest mechanisation of the future. Proceedings of the 52nd International Symposium on Forestry Mechanization. Sopron, Hungary: University of Sopron Press, 2019. P. 379—393. URL: https://www.fs.usda.gov/nrs/pubs/jrnl/2019/nrs_2019_-george_001.pdf. Text. Image: electronic.
Будник П. В., Баклагин В. Н., Галактионов О. Н. Лесоэксплуатационное районирование лесных субарктических территорий // Известия высших учебных заведений. Лесной журнал. 2023. № 6. С. 114—135. DOI: 10.37482/0536-1036-2023-6-114-135.
Сукачёв В. Н. Избранные труды. Т. 1. Основы лесной типологии и биогеоценологии. Л.: Наука, 1972. 418 с.
Goodsite M. The Future of Shipping Minerals from the Arctic // Towards a Sustainable Arctic: International Security, Climate Change and Green Shipping. 2023. P. 231—244. DOI: doi.org/-10.1142/9781800613225_0011.
Hartwell C. A. In our (frozen) backyard: the Eurasian Union and regional environmental governance in the Arctic // Climatic Change. 2023. Vol. 176, no. 4. P. 45. DOI: doi.org/-10.1007/s10584-023-03491-7.
Schreiber J. B. Issues and recommendations for exploratory factor analysis and principal component analysis // Research in Social and Administrative Pharmacy. 2021. Vol. 17, no. 5. P. 1004—1011. DOI: doi.org/10.1016/j.sapharm.2020.07.027.
Jaeger A., Banks D. Cluster analysis: A modern statistical review // Wiley Interdisciplinary Reviews: Computational Statistics. 2023. Vol. 15, no. 3. P. e1597. DOI: doi.org/10.1002/-wics.1597.
Härdle W., Simar L. Applied multivariate statistical analysis // Springer, Berlin — Heidelberg. 2019. Vol. 10. P. 978-3. DOI: doi.org/10.1007/978-3-030-26006-4.
Myung I. J. Tutorial on maximum likelihood estimation // Journal of mathematical Psychology. 2003. Vol. 47, no. 1. P. 90—100. DOI: doi.org/10.1016/S0022-2496(02)00028-7.
Kaiser H. F. The application of electronic computers to factor analysis // Educational and psychological measurement. 1960. Vol. 20, no. 1. P. 141—151. DOI: doi.org/10.1177/-001316446002000116.
Kaiser H. F. The varimax criterion for analytic rotation in factor analysis // Psychometrika. 1958. Vol. 23, no. 3. P. 187—200. DOI: doi.org/10.1007/BF02289233.
Kaiser H., Rice J. Little jiffy mark IV. Educational and Psychological Measurement 34. 1974. DOI: 10.1177/001316447403400115.
Williams B., Onsman A., Brown T. Exploratory factor analysis: A five-step guide for novices // Australasian journal of paramedicine. 2010. Vol. 8. P. 1—13. DOI: doi.org/10.33151/ajp.8.3.
Nielsen F., Nielsen F. Hierarchical clustering // Introduction to HPC with MPI for Data Science. 2016. P. 195—211. DOI: doi.org/10.1007/978-3-319-21903-5_8.
Coates A., Ng A. Y. Learning feature representations with k-means // Neural Networks: Tricks of the Trade: Second Edition. Berlin; Heidelberg, 2012. P. 561—580. DOI: doi.org/10.1007/-978-3-642-35289-8_30.
Planning methods and decision support systems in vehicle routing problems for timber transportation: a review / J. F. Audy, M. Rönnqvist, S. D’Amours [et al.] // International Journal of Forest Engineering. 2023. Vol. 34, no. 2. P. 143—167. DOI: doi.org/10.1080/14942119.-2022.2142367.
Dems A., Rousseau L. M., Frayret J. M. Annual timber procurement planning with bucking decisions // European Journal of Operational Research. 2017. Vol. 259, no. 2. P. 713—720. DOI: doi.org/10.1016/j.ejor.2016.10.039.
Zykov S. V., Dayneko D. V. The Analysis of the Russian Forest Industry // Forest Industry of Russia: Smart Innovations and Success Stories. Singapore: Springer Singapore, 2022. P. 17—103. DOI: doi.org/10.1007/978-981-16-9861-3_2.
Senko S. Nordic forest solutions as an opportunity to reform the forestry sector in Russia: A case study in the Republic of Karelia // Dissertationes Forestales. 2021. Vol. 320. 61 p. URL: https://web.archive.org/web/20211012192823id_/https://dissertationesforestales.fi/pdf/-article10645.pdf. Text. Image: electronic.

Еще

Статья научная