Тэта-функции в математической модели шума квантования

Получение требуемого математического выражения для двух и n -мерных плотностей распределения вероятностей при функциональных преобразованиях случайных векторов наталкивается на математические трудности, связанные с необходимостью выполнения большого объема математических преобразований.

Авторы предлагают решение, позволяющее в некоторых случаях избавляться от выражений, содержащих кратные ряды. Новую формулу и способ, которым она была получена, вместе со способом, с помощью которого была получена исходная формула (1), можно применять для функциональных преобразований случайных векторов. И, в частности, для таких преобразований, в которых участвуют одновременно несколько двухмерных случайных векторов.

В работе [1] была получена математическая модель двухмерной плотности распределения вероятности для шума квантования с использованием двухмерного преобразования Фурье и метода характеристической функции способом, рассмотренным в [2]. Шум квантования возникает при квантовании суммы вектора теплового шума ш ( ш,. ш₂ ) и вектора, вызванного отражением электромагнитных волн от капель дождя £ fe . ^ 2 ) или водосодержащих объектов в моменты времени соответственно t и t .

В разделе 1 приведено выражение для плотности распределения в виде двойной бесконечной суммы. В разделе 2 приводятся выкладки, приводящие это выражение к виду, содержащему только тэта-функции. В заключении описаны достоинства полученной формулы.

• 1.    Постановка задачи

Известно, что шум квантования возникает в любой системе обработки данных. Как только аналоговый сигнал любого происхождения преобразуется в цифровой код, пригодный для обработки компьютерной программой самого разного назначения или в ап- паратуре реального времени, так сразу же на него аддитивно накладывается шум квантования. Значение шума квантования в каждый момент времени равно разности между значением отсчета, подвергаемого квантованию, и результата квантования. Шум квантования ухудшает характеристики работы и аппаратуры и программ, обрабатывающих данные. Ухудшаются не только указанные характеристики, но и математически существенно усложняются преобразования при вычислении нужных характеристик.

Плотность распределения вероятности шума квантования в статье [1] описывается следующим выражением:

... w (    \   1 V V ''2+2’1 П1

W _z = W _z ( U i ,u 2 ) = -2 Е Е e ^в          cos— ( nu + n 2 u 2 ) ,

А n1=-^ n2 =-^

I А I I А iфу, u’i-j;

где Z ( Z , Z ) — вектор шума квантования согласно определению, данному в [2];

• А — шаг квантования;

• 2.    Математические преобразования

в — глубина квантования координат вектора, порождающего шум квантования, численно равная отношению квадрата шага квантования к значению дисперсии координат вектора;

р — коэффициент корреляции координат вектора, порождающего шум квантования, разнесенных на некоторый интервал времени.

В выражении (1) для краткости записи введем следующие обозначения:

W f = 4 Е Е e" t ^{( P} mⁿ + ^{n )} cos ( mz^ + nz ₂ ) =

^А m =-® n =-®

¹ \ ’ - 1 ( m ² + 2 P mn + n ² )__,„,          ,        1

= —Е e          ' cos ( mz^ + nz ₂) ,

^А m , n

I z i| ^{- n} ,      \^z i| ^{- n} .

Здесь

2 п^г

1 = в '

m = nx, n = n2;

z ₁

2 n

= ^U iT" , А

z ’    ^u ’

2 n

• А

Выразим плотность распределения вероятности через тета-функции Якоби, которые, согласно их определению, приведенному в [3] и [4], имеют следующий вид:

1 м

^i (z, q)=2 q4 L(-1) nqn(n+1) sin(2 n +1)z, n=0

• ¹    м                                   м I n + ¹ ]

^ (z,q) = 2q4 Lqn(n+1) cos(2n +1)z = Lq4 22 cos(2n +1)z,(6)

n = 0

м 2м 2

^(z,q) = 1 + 2^qn cos2nz = Lqn cos2nz,(7)

n = 1

мм

^(z,q)= 1 + 2^(-1)nqn cos2nz = L(-1)nqn cos2nz ,(8)

n = 1

где z — аргумент тэта-функций, q — параметр Якоби, определенный в [3].

Для удобства последующих преобразований введем следующее обозначение:

Т-

2П-

*= в' e = e .

Показательную функцию под знаком суммы в выражении (2) преобразуем в произведение двух сомножителей, каждый из которых зависит только от одного индекса суммирования. Для этого используем прием, описанный в [5] и заключающийся в дующей замене индексов суммирования:

m = ( i + j )/2 , n = ( i - j )/2 .

Тогда выражение (2) примет следующий вид:

сле-

1          - /^i ^ f b + p j + j ^ ^b p ) )

W? = У е    ²

z i,j

I ( i + j )     ( i - j )

cos -—— z . + -—— z.

\  2     ¹      2     2 4

, z 1| <  П,

I ^z 1l <  ⁿ

Выражение (11) можно представить в виде двух бесконечных мирования которых i и j также изменяются от - м до + м :

сумм, индексы

сум-

L e" i , j нечетные

w, = 4 ^z   A ²

^- t ⁽ i ^{2 ( 1 + p} ) + ^{j 2 ( 1 - p} ) )

^- t ⁽ i ^{2 ( 1 +} p ^{) +} j ^{2 ( 1 -} p ) )

Le     2     xcos i , j четные

x cos

4 + j ) z + < i - j)

4   2

)

z 2

+

iX i + z )  ₊( i - z >   )

П ^z 1 ⁺ _n z 2 4   ^{2         2}     4

X

,

I ^z 1l <  П   l ^z 2I <  ⁿ .

Применяя формулу сложения для функций косинус в суммах, входящих в формулу (12), вместе с подстановкой вида:

x , =( z_x + z ₂) /2 ,     x ₂ =( z_x - z ₂) /2 ,                            (13)

разобьем формулу (12) на четыре суммы. В результате этих преобразований формула

• (12)    примет следующий вид:

  W , = ^_r ( S 1 ( X 1 , x 2 ) + S 2 (

  
  

_чX j, x ₂) + S ₃( x , x ₂) + S ₄( x , x ₂)) , l x + x ₂1< n , l x - x ₂1< n ,     ⁽¹⁴⁾

где:

⁵ 1 ⁽ x i , x 2 ) =

V i

- 1 ( 1 + p ) i¹

Z e 2 cosix четное

— ' ^{( 1 +} p ) j j

Ze г

четно е

А

52 (xi, x2 ) =

- ' ( 1 + p ) i¹

Z e ² cos ix

V i нечетное

- ' ( 1 — p ) J ²

Ze г

cos ^jX 2   ,

A

⁵ 3 ⁽ x i , x 2 ) =

—

(          — ' ^{( 1 +} p ) i ²

Z e ²

V i четное

- 1 ( i — p ) j ²

cos jx 2   ,

A

⁵ 4 ⁽ x i , x 2 ) =

—

V

- ' ( 1 + p ) i^г

Z ^{e 2}

i нечетное

sin ix   Z e ²

— ' ^{( i - p} ) ^j j

^{Z e 2}

V j нечетное

Sin ^jx 2   ,

A

sin ^jx 2   .

Функции sin ix и sin jx ₂ , входящие в выражения (17) и

(18), являются нечетными.

( X i , x ₂) индексам суммиро-

Поэтому в суммах-сомножителях выражений 5 ₃ ( X j, x ₂) и 5 4

вания, отличающимся знаком, соответствуют члены с противоположным знаком, которые уничтожаются. По этой причине значения выражений 53 (xx, х2) и 54 (xx, х2 ) окажутся равными нулю. Тогда в выражении (14) слагаемые 53 (xx, х2 ) и 54 (Xj, x2 ) можно опустить и переписать его в следующем виде:

W Z    ^ ^{( 5} 1 ⁽ x i , x 2 ) + ⁵ 2 ⁽ x i , x 2 ))’

| X i + x ₂1 <  П .

В суммах выражения (15) выполним замену индексов суммирования вида i = 2 к и j = 2 к , а в суммах выражения (16) выполним замену i = 2 к + 1 и j = 2 к + I . В результате выражения (15) и (16) примут следующий вид:

S 1

TO

5 2 = Z e

Z e 2 ' ^{( i + p} ) ^к cos2 кх_х

- ' ( 1 + p ) ( 2 к + 1 ) ² 2

V к =-to

( TO

' Z e к =-to

V

TO

Z e 2 ' ^{( i - p} ) ^к cos2 кх₂

cos ( 2 к + 1 ) x _i   Z

TO     — t ^{( i -} p ) ( 2 ^{к + i ) 2}

e

cos

A

к =-to

TO

,

A

x ₂

А

^cos ( ^{2 к} + ^{i )} x i   Z

e

co

x ₂

.

к =-to

V

В выражениях (20) и (21) введем следующие обозначения:

q , = e ”2 ' ^{( l + p} ) , q 2 = e

.

После введения обозначений (22) в выражения (15) и (16) формула (19) может быть за- писана в следующем виде:

+

(         ( 1

Z д\ ^{+ 2 7} c^oS

V к =-to

W Z =

А ²

x ₁

TO

A

V   к ²      <^1      V    к ²     - 7     ,

Z q i cos2 кх₁   Z ^ 2 cos2 кх₂ +

V V к =-to

: -TO

(.   1

Z q2V+ 27 coS к=-to

x ₂

, | x ₃ + x ₂1< n ,     |x ₃ - x ₂1< П .

Тогда формула (23) преобразуется к следующему виду:

W _Z = ^2 ( ⁹ з ( ^x i, q , ) ⁹ з ( ^x 2 ,q 2 ) + ⁹ 2 ( ^x i, q , , ) ⁹ 2 ( ^x 2 ,q 2 ) ) , l- x ^{+ x} 21 ^{5 п} , l ^x , ^{- x} 21 ^{5 п} .⁽²⁴⁾

Если в выражении (24) перейти к обозначениям формулы (1) и последовательно выполнить обратные подстановки для перехода к переменным u и u , то в результате формулу (24) можно переписать в следующем виде:

W Z ^(ui , u 2 ) =

¹      —

^ ⁹¹ A ^{( u + u} 2

A

) e    °* ^Р )

- 4 - ², ^п(и              ^{a+ P} )

^{+ 9} 1 д ^{( U} 1 ⁺ u 2 ) , ^e

7A               7

4A( и , 7

—

9з f "("I

-4 п ²z 2

A ( P) u2), e p

—

-4 —² U А а п ^{( р} ) u ₂), e ^р

, И A,

+

I u 21 sA .

В заключение опишем принцип получения иных аналитических выражений для формулы (1), используя свойства симметрии тэта-функций Якоби [6].

Все свойства симметрии тэта-функций можно условно разбить на три группы, касающиеся характера изменения вида аналитического выражения для плотности распределения вероятности шума квантования, выраженного через тэта-функции.

Первая группа свойств симметрии связана с изменением аргумента тэта-функции на четверть периода у функций 9 ( x , q ) , 9 ₂ ( x , q ) и на половину периода у функций 9 3 ( x , q ) , 9 ( X , q ) . Эти свойства симметрии тэта-функций позволяют получить новые аналитические выражения для (1) с помощью подстановок в (24), которые имеют следующий вид:

f   —I

• ⁹ , ^x +-, q = ⁹ 2 ^{( x} , q ) ,

7    27

f   —I

• ⁹ 2    ^x + -, q = ^{- 9} i ^{( x} , q ) ,

7    27

f   —I

• 9 з x + -, q = 9 4 ( x , q ) ,

7    2

I ^П I

9 I x + 2", q I = 9 ( x , q ) .

Эта первая группа свойств симметрии тэта-функций (26) – (29) проявляется образовании одного вида тэта-функций в другой и позволяет получить полное ство формул, эквивалентных формулам (24) и (25). Используя свойства (26)

в пресемей-– (29)

можно составлять выражения полностью Например, выражение вида:

тождественные выражениям

(24) и (25).

Wz =^19

x, + - , q, 94

2 7   7

— I

x2 +- ,q2

2 7   7

I x_x + x ₂1 5 -, l x

+ 9

п I ^x i ⁺ т , 2 7

q , 9 1 l x ₂ + -\

7  77      ² 7

q2

,

- x2I 5 -

и равносильное ему выражение:

W z ( « 1 , u 2 ) = J2 ⁶ 4 Л (,

п

«« 1 ⁺ « 2 ⁾⁺ п

, e

4 л ²

. "в " ⁽¹ + ^Р )

\

У

А П(     п л

+ 6 1 —⁽ u i + u 2 ) + —

к

к

к

У

6 4 А ( «

—

к

п

« 2 ⁾⁺^

— 4 п ²

, e

в

- ( 1 ^- р )

\

У

+

, e

4 л ²

------( 1 + Р ) . в

\

У

6 1 П ( _И 1

—

У

к

п

« 2 ⁾⁺^

, e

— (1 — Р ) , в

А

, l u ll ^ 2,

।    । А

I « 2I ^~

являются выражениями, эквивалентными выражениям (24) и (25) соответственно. Рассмотрев выражения (26)–(29) и (24), нетрудно увидеть, что можно получить четыре формулы, эквивалентные формуле (24). Во всех полученных выражениях тэта-функция подсчитывается очень быстро (см., например, [6]). Используя формулу (25), построим график двухмерной плотности распределения шума квантования, который изображен на рисунке.

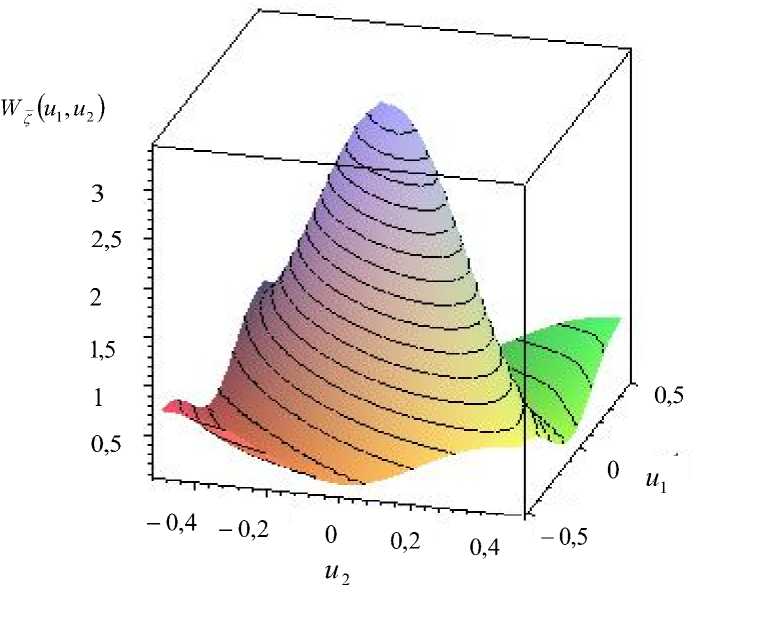
Рис. Плотность вероятности по формуле (25)

(параметр t = 1,3, шаг квантования А = 1, коэффициент корреляции р = 0,7)

Заключение

В работе получена новая формула, выражающая двухмерную плотность распределения вероятности шума квантования (1) в виде выражений (24), (25), (30), (31), состоящих только из тэта-функций Якоби. Первая задача, которую позволяет решить данная формула, это возможность избавиться от кратных функциональных рядов и тем самым упростить преобразования при некоторых статистических и вероятностных расчетах. Вторая задача, которую позволяет решить данная формула и которая может возникать при разработке программ и проведении модельных экспериментов, это уменьшение вычислительной работы при одновременном уменьшении погрешностей вычисления. Для плотности распределения вероятности (1) актуальна задача увеличения скорости сходи- мости функциональных рядов при допустимой погрешности вычислений. Эта задача решается для некоторых значений параметра Якоби c использованием тэта-функций Якоби из библиотек известных математических пакетов. Применяя формулы (24), (25), (30), (31) можно повысить скорость вычисления функции W~ (ux,u2) при той же точности вычислений, что и для выражения (1). И, наконец, используя способ получения исходной формулы, изложенный в [1], полученные результаты можно обобщить по аналогичной схеме на плотности распределения вероятности вида (1), но имеющие большую размерность.

Статья подготовлена при поддержке правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.А03.21.0011