Тканевый композит. Оценка упругодиссипативных характеристик

В настоящее время тканевые композиты широко используются в различных областях промышленности: из них изготавливают панели вагонов транспортных средств, элементы крыльев и фюзеляжа летательных аппаратов, емкости для транспортировки агрессивных сред, лопасти ветроэнергетических установок, вертолетов и т.д. [1, 2]. Подобная популярность тканевых композитов объясняется благоприятным сочетанием высоких характеристик жесткости и прочности вдоль волокон при относительно низкой трудоемкости их изготовления по сравнению с однонаправленными материалами.

Одной из важных задач на стадии разработки проекта конструкции является оценка эксплуатационных характеристик материала, что приводит к необходимости математического моделирования его свойств. Определению характеристик упругости тканевых композитов посвящены работы А.М. Скудры и Ф.Я. Булавса [3, 4], где материал рассматривается в виде двух условных монослоев основы и утка, однонаправлено армированных искривленными волокнами, а искривление волокон учитывается чередованием наклонно и продольно армированных полос. В настоящее время тканевые композиты, как правило, моделируют с использованием пакетов прикладных программ, основанных на использовании метода конечных элементов, таких как ANSYS, ABACUS, LS DYNA, NASTRAN и т.д. [5–9]. Однако возможности разработчиков подобных моделей ограничиваются сложностью структуры материала, так как тканевый композит состоит из матрицы и армирующей ткани, состоящей из нитей, которые в свою очередь состоят из волокон. Кроме того, иногда в расчеты включают интерфейсный слой между волокнами и матрицей. Подобное разнообразие неоднородностей ведет к необходимости ограничиваться одним из уровней детализации композита: макроуровнем, мезоуровнем, микроуровнем и т.д. На макроуровне тканевый композит рассматривают как однородный ортотропный материал. На мезоуровне – как неоднородную среду, состоящую из матрицы (связующего) и нитей, свойства которых обычно усредняют по правилу смесей [1–4], либо пренебрегают наличием матрицы в композите, оставляя при этом только волокна. На микроуровне приходится учитывать неоднородность нитей, состоящих, в свою очередь, из волокон и матрицы.

В данной работе предложена численная модель тканевого композита, где упругодиссипативные свойства материала определяются соответствующими свойствами однонаправленного композита с теми же структурными компонентами и объемной долей волокон (мезоуровень). Предложенная модель позволяет учесть тип переплетения нитей (полотно, саржа, сатин и др.).

Основные соотношения расчетной модели

Согласно разработанной модели, тканевый композит схематизирован, как показано на рис.1 (в качестве примера рассмотрена ткань полотняного переплетения). В основе предложенной модели лежат следующие допущения:

• 1.    Изогнутые участки нитей (волокон) заменены прямолинейными участками.

• 2.    Структура материала регулярна, что позволяет ограничиться рассмотрением одного представительного элемента объема (жирные прямоугольники на рис. 1).

• 3.    Представительный элемент объема - это набор ячеек, соединенных в цепь последовательно либо параллельно.

• 4.    Каждая ячейка содержит однонаправленный композит с различной ориентацией волокон и с теми же структурными компонентами, что и тканевый композит.

• 5.    Тип переплетения нитей (полотно, саржа, сатин) определяет только длину kl прямолинейных участков нитей, заданную с помощью коэффициента длины k , и не влияет на угол θ наклонных участков нитей.

• 6.    Волокна распределены по объему ячеек равномерно с одинаковым объемным содержанием.

• 7.    Материал ячеек является сплошным, однородным, ортотропным и линейно упругим.

• 8.    Напряженно-деформированное состояние ячеек однородно, то есть в процессе деформирования ячейки не искривляются, а нити (волокна) в ячейках остаются прямыми.

• 9.    Рассмотрено плоское напряженное состояние ячеек.

• 10.    Потери энергии в единице объема материала определяются суммой потерь энергии в каждой ячейке.

• 11.    Отношение длин участков нити друг к другу определяется коэффициентом длины k (коэффициент k , равный единице, соответствует полотняному переплетению нитей, двум – саржевому переплетению, а восьми – сатиновому).

В основе предложенного метода лежит теория слоистых пластин [1–4, 10], согласно которой матрицы тензоров напряжений [σ], деформаций [ε] и податливости [ S ] имеют следующий вид:

					-1-	0	A lt
[ ст ] =	CT L T LT	. и=	e l Y lt	.     [ S ] =	E L 0	1 G LT	E L 0	.                  (1)
	. ст т _		. £ T .		_ A lt . El	0	1 E T J

Здесь координата σ представляет нормальное напряжение в плоскости ортотропии, τ – касательное напряжение, ε – линейную деформацию, γ – модуль сдвига, E – модуль упругости, G – модуль сдвига, а µ – коэффициент Пуассона. Индекс « L » соответствует направлению вдоль волокон однонаправленного композита, « T » – поперек волокон, а индекс « LT » обозначает сдвиговое направление.

Удельная энергия диссипации Δ W однонаправленного линейно упругого композита определяется выражением

Л W = 2 [ст |>||ст ],                                 (2)

где [Ψ] – это матрица упругодиссипативных характеристик (УДХ) по напряжениям:

	^L. E L	0	_ A lt V l E L
[ V ] =	0	V lt GLT	0	.                                        (3)
	A lt V l	0	V t
	El		E T

Здесь ψ _L – представляет коэффициент диссипации однонаправленного композита вдоль волокон, ψ T – коэффициент диссипации поперек волокон, а ψ LT – сдвиговый коэффициент диссипации.

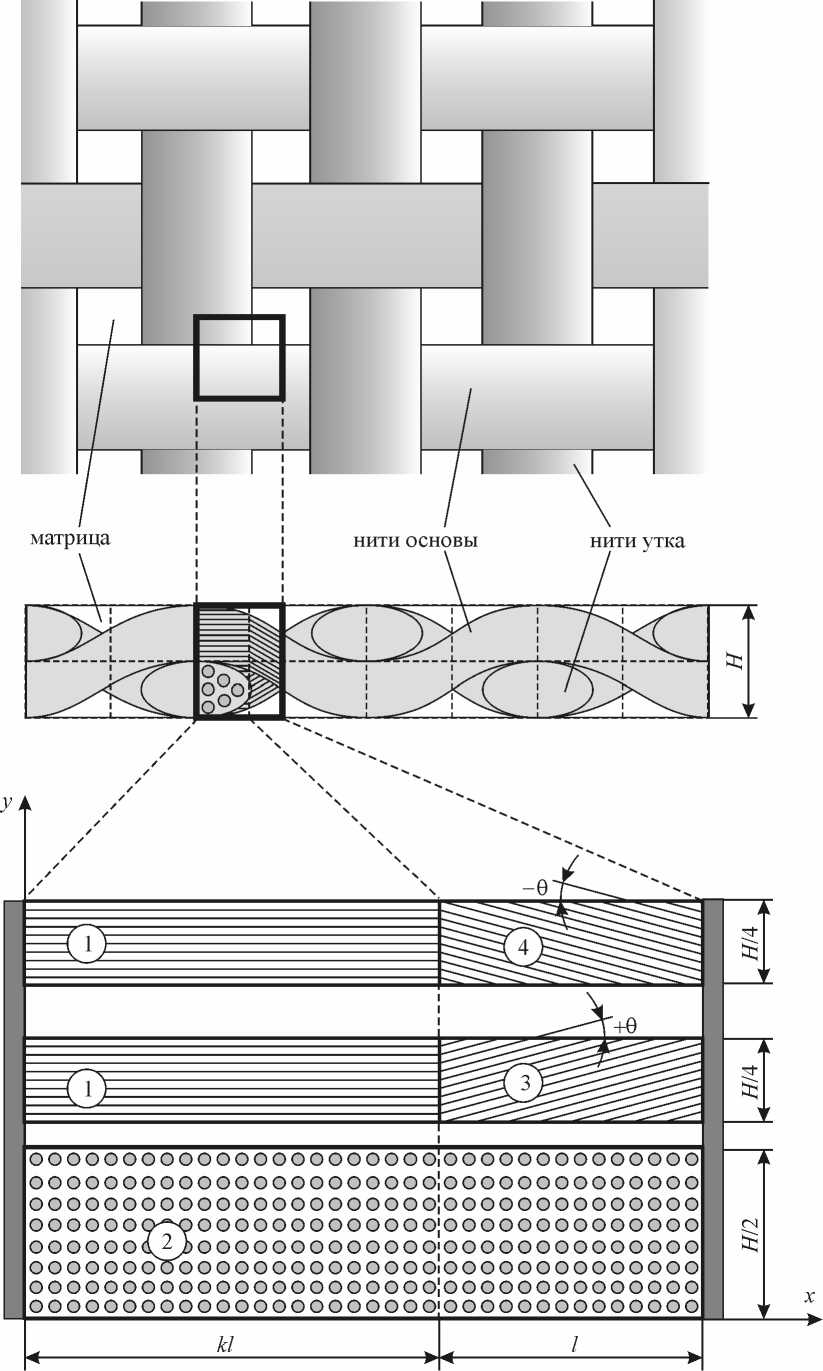
Рис.1. Схематизация тканевого композита

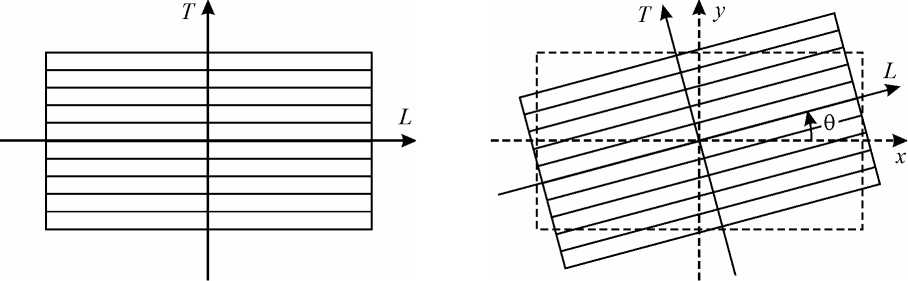
а) однонаправленный композит в естественной системе координат {LT}

б) однонаправленный композит в системе координат {LT}, повернутой относительно системы координат {xy} на угол θ против часовой стрелки

Рис. 2. Схема поворота осей координат монослоя

Для определения матриц УДХ и податливости однонаправленного композита в системе координат { xy } (рис. 2, б ) достаточно заменить матрицу напряжений в формуле (2) следующим выражением:

И = [ R ] [ а ^{ LT } ] , (4) где матрица [ σ ^{{ LT }} ] – это матрица тензора напряжений однонаправленного композита в естественной системе координат { LT }, а матрица [ R ] – это матрица поворота на угол θ по часовой стрелке

	cos 9 2       sin 9 cos 9      sin 9 2
[ R ] =	- sin 9 cos 9 cos 9 2 - sin 9 2 sin 9 cos 9	.                               (5)
	sin 9 2       - sin 9 cos 9     cos 9 2

При этом матрицы податливости и УДХ в системе координат { xy } принимают вид:

[S9 ] = [R] [S{LT} ] [R]T,       [V9 ] = [R] [T LT} ] [R]T,                       (6)

а характеристики упругости и диссипации определяются следующими выражениями:

E9 = —

E x 9 ’

S 11

E9 = —

E y   9 ’

S 33

g9

xy

95" , S 12

P ^ y

S 13

9 9 , S 11

■⁹ —ХМ⁹ V⁹    -⁹ _Ш ⁹ p^{9    9} _XM⁹ Q⁹

W x = ^T 11 E x ,    V y = ^T 33 E y ,    т xy =^T 12 G xy .

Для вывода выражений, определяющих характеристики упругости пластика, армированного тканью, полагали, что при деформировании материала в направлении оси x ячейки № 1 и № 3 (а также № 1 и № 4) соединены друг с другом последовательно, а блоки ячеек № 1 и № 3, № 1 и № 4

и № 2 работают параллельно, как показано на рис. 1. При деформировании материала в направ- лении оси y, а также в сдвиговом направлении полагали, что все ячейки работают параллельно. В результате были получены следующие выражения для определения модулей упругости Ex и Ey, модуля межслойного сдвига Gxy, а также коэффициентов Пуассона µxy и µyx:

E x

( k + 1) E_lE⁹_x   E_{t  с}   (2 k + 1) E_T + E⁹_y

xT л +   , E ^

2( E _l + kE ⁹ _x)   2 ^y 2( k + 1)

k ( ^Glt ^{+ G}tt ) ⁺ G ⁹ y ^{+ G}tt _(k ⁺ 1) P LT p " y p TT _E y

, ^P xy =             0 X ⁺ n  , ^P yx = г ^P yx .

²⁽ k ⁺ 1)                2( P lt + k p ⁹ y )   ²         E x

Здесь G TT – это модуль сдвига ячеек № 2 в плоскости { xy }, а µ TT – соответствующий коэффициент Пуассона.

Коэффициенты диссипации материала ψ x , ψ y и ψ xy в системе координат { xy } определяются путем подстановки в выражения (8) модулей упругости, отнесенных к соответствующим коэффициентам диссипации:

¥ x = E x

( k + 1) E _l E ⁹¥ l ¥ x

ET

- 1

______________ ^z L x ' L' x __+ T

_ 2¥ _l¥^ El _¥⁹+ kE ⁹ _¥ L ] ² ¥ t _ ,

¥y = E

2 k +1 E_t --- +

e9

2( k + 1) ¥ t  2( k + 1) V

. 9

- 1

, (9)

^¥ xy   G xy

k

' GL^ + GTT ) + _d

G 9

xy

- 1

^{2( k +} 1) v ^¥ LT   ^¥ tt

2( k + 1) V 9 y

+

2( k + 1) ¥ tt

.

Здесь ψ_TT – это сдвиговый коэффициент диссипации ячеек № 2 в плоскости { xy }.

Обсуждение результатов

В работе были вычислены зависимости УДХ тканевых композитов в зависимости от коэффициента длины нитей. В качестве исходных данных для расчетов использовали характеристики однонаправленного стеклопластика GLASS/DX210, взятые из работы [11] и приведенные в табл. 1. Модуль сдвига G_TT определили с учетом квазиизотропии материала ячеек № 2 в плоскости { xy }, приняв коэффициент Пуассона µ TT равным µ LT , а сдвиговый коэффициент диссипации ψ TT приняв равным ψ T . Угол θ определили с использованием микрофотографий срезов тканевого композита, взятых из работы [12], он составил примерно 25°. При схематизации материала полагали, что тип переплетения нитей влияет только на величину коэффициента длины, тогда как угол θ от него не зависит, а число нитей основы и утка совпадает.

Таблица 1

УДХ однонаправленного стеклопластика GLASS/DX210

Наименование параметра	Модули упругости		Модули сдвига		Коэффициенты Пуассона		Коэффициенты диссипации
Обозначение	E L , ГПа	ET , ГПа	G LT , ГПа	GTT , ГПа	µ LT	µ TT	ψ L , %	ψ T , %	ψ LT , %	ψ TT , %
Величина	37,8	10,1	4,9	4,0	0,29	0,29	0,87	6,1	6,9	6,1

Таблица 2

УДХ тканевых стеклопластиков

Тип переплетения нитей	Модули упругости		Модуль сдвига	Коэффициент Пуассона	Коэффициенты диссипации
	продольный	поперечный			продольный	поперечный	сдвиговый
	E x , ГПа	E y , ГПа	G xy , ГПа	µ xy	ψ x , %	ψ y , %	ψ xy , %
Полотно	11,1	8,92	5,56	0,36	5,66	6,18	6,40
Саржа	12,9	9,32	5,18	0,33	5,19	6,15	6,44
Сатин	17,9	9,84	4,66	0,30	3,48	6,17	6,49

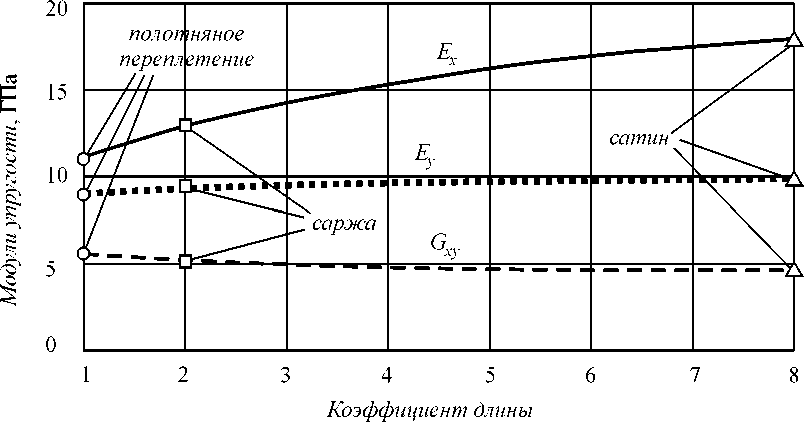
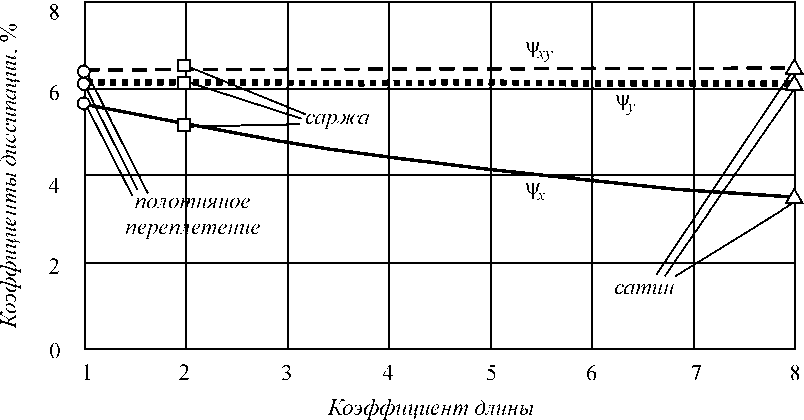
Результаты расчетов УДХ приведены на рис. 3 (рис. 3, а отражает зависимости модулей упругости E x , E y и G xy материала от коэффициента k , рис. 3, б – коэффициентов диссипации ψ x , ψ y и ψ xy , а рис. 3, в – коэффициентов Пуассона µ xy и µ yx ). Точки на рис. 3 соответствуют различным типам переплетения нитей (круги – полотняное переплетение, квадраты – саржевое, а треугольники – сатиновое). Величины УДХ тканевого материала, вычисленные с использованием предложенной модели, в зависимости от типа переплетения нитей приведены в табл. 2.

Расчеты показали, что продольный модуль упругости тканевого композита снизился примерно в 2–3 раза по сравнению с однонаправленным материалом, тогда как продольный коэффициент диссипации существенно возрос (примерно в 3–5 раз). Это объясняется, во-первых, наличием у тканевого композита нитей, расположенных в двух перпендикулярных направлениях (основа и уток), а во-вторых, наличием у нитей наклонных участков (ячейки 3 и 4 на рис. 1). При растяжении тканевого композита в направлении оси x угол наклона нитей основы уменьшается – происходит распрямление нитей основы, при этом нити утка деформируются в поперечном направлении, которому соответствует низкая жесткость и высокий коэффициент диссипации (по сравнению с соответствующими характеристиками в направлении нитей основы). Аналогичная ситуация возникает при растяжении материала в направлении нитей утка.

Сравнение трех различных типов переплетения нитей показало, что наибольшей жесткостью обладает материал, армированный тканью сатинового переплетения. Продольный модуль упругости сатинового композита на 61 % выше по сравнению с композитом, армированным тканью полотняного переплетения. При этом продольный коэффициент диссипации сатинового композита принимает наименьшее значение (на 40 % меньше, чем у полотняного композита). Это объясняется соотношением длин наклонного и прямого участков нитей: чем меньше размер l ячеек с наклонными волокнами по сравнению с общей длиной представительного объема ( k +1) l , тем выше жесткость материала в продольном направлении и тем ниже соответствующий коэффициент диссипации. Величины поперечного и сдвигового коэффициентов диссипации (также как и соответствующие модули упругости) практически не зависят от типа переплетения нитей.

Заключение

В работе предложена расчетная модель, позволяющая с использованием УДХ однонаправленного композита оценить УДХ тканевых композитов с теми же структурными компонентами при той же объемной доле волокон. Согласно разработанной модели, представительный элемент тканевого материала рассматривается в виде последовательного и параллельного соединения ячеек, содержащих однонаправленный композит с теми же структурными компонентами при той же объемной доле волокон. Модель позволяет учитывать тип переплетения нитей.

С использованием предложенной модели в работе выполнены расчеты УДХ тканевого стеклопластика на основе данных об однонаправленном стеклопластике GLASS/DX210. Расчеты показали, что с точки зрения диссипативных характеристик в продольном направлении однонаправленный композит значительно уступает тканевым материалам, тогда как с точки зрения характеристик упругости ситуация противоположна. Продольный коэффициент демпфирования тканевых композитов примерно в 3–5 раз выше, чем продольный коэффициент демпфирования однонаправленного стеклопластика с теми же структурными компонентами при той же объемной доле волокон. Продольный модуль упругости тканевых композитов при этом снизился примерно в 2–3 раза по сравнению с соответствующим однонаправленным материалом.

Сравнение трех типов переплетения армирующей ткани (полотняное переплетение, саржевое и сатиновое) показало, что наибольшей жесткостью обладает материал, армированный тканью сатинового переплетения: продольный модуль упругости сатинового композита на 61 % выше по сравнению с композитом, армированным тканью полотняного переплетения. Продольный коэффициент диссипации сатинового композита при этом принимает наименьшее значение (на 40 % меньше, чем у композита с полотняным типом переплетения).

а)

б)

в)

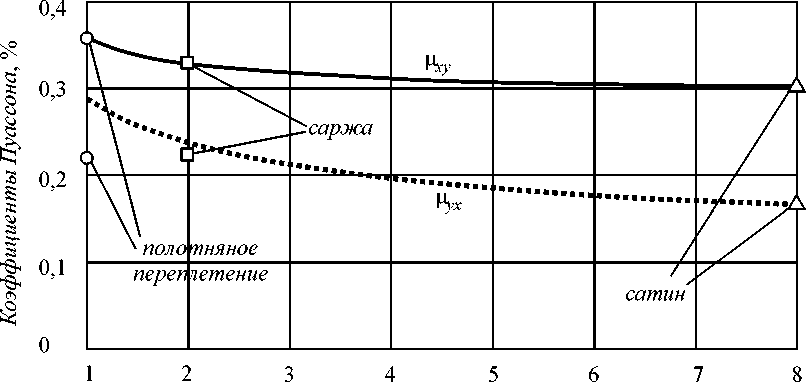
Коэффициент длины

Рис. 3. Зависимость УДХ тканевых стеклопластиков от коэффициента длины нитей

Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации в рамках комплексного проекта «Создание высокотехнологичного производства модельного ряда энергосберегающих низкопольных трамвайных вагонов модульной конструкции» по договору № 02.G36.31.0002 между Министерством образования и науки РФ и ФГУП ГКНПЦ им. М.В. Хруничева в кооперации с головным исполнителем НИОКТР – ФГБОУ ВПО ЮУрГУ (НИУ).