To substantiate Mach's principle

To substantiate Mach's principle

Annotation

The relationship between the inert and gravitational masses on Earth has been established. It is shown that Mach's principle and the principle of equivalence of inert and gravitational masses can be investigated experimentally.

There is a well-known Mach principle, which states that the inert properties of each physical body are determined by all other physical bodies in the Universe and depend on their location [1]. The first idea to test this principle is to temporarily remove all bodies in the universe. But the current amount of technology is not enough to implement this idea. And therefore (and until the "salutary" idea of unknowability has not finally taken possession of the minds, as happened, for example, in quantum mechanics), we will try to understand how the Earth could create inertia (all the other bodies of the Universe without us, someone pushed to sufficient distance).

How could the Earth create an inertial force acting on an accelerating body? Maybe, about the same as a large stationary electric charge on another accelerating charge ... After all, there between electrodynamics and gravitomagnetism, which are described by the same Maxwell equations, are many analogies - see for example [2].

Consider an electric charge q moving relative to the charge Q with acceleration a. The strength of the electric field E, created by the charge q at the center of the charge Q, is determined by the Larmor formula [3]. In

the case when the speed of the charge is much less than the speed of light c, this formula takes the form [4]:

_F ~ q[nx ^[ nxa ^] ]

~ c2R , where R is the distance between charges, and n is the unit vector of the vector R directed from charge q to charge Q - see Fig. 1. If the acceleration vector a is directed perpendicular to the vector R, then the vector

Ео = [n х [n x a]], and vector a are related by the relation

Ео = -a

• - see Attachment. From (1, 2, 3) it follows that the charge Q from the side of charge q is acted upon by the force

• F. = ^Ео = a(4)

By virtue of Newton's second law, a force acts on the charge q from the side of the charge Q

FQ = —F, = —-a

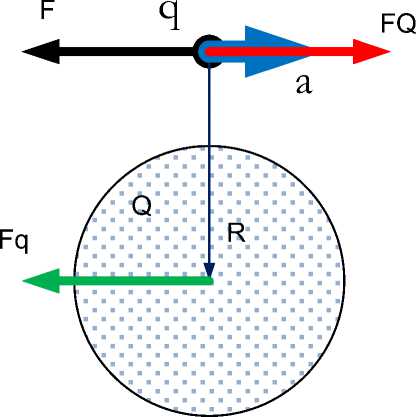
Fig. 1.

Suppose, by analogy, that the accelerated motion of mass is also described by equation (1), where q is the gravitational mass, and E is the gravitational strength. Let us consider the case when the mass q moves in the field of another mass Q at a distance R → ∞ from the center of this mass in the plane perpendicular to the vector R . In this case, all the previous conclusions are applicable. Therefore, the body Q acts on the body q by force (5) and the force vector is directed parallel to the acceleration vector a .

The force that moves the mass q with acceleration a , ^F q = m q a

where m_q is the inert mass of the gravitational mass q. Thus, two oppositely directed forces act on the mass q (5, 6). According to Newton's second law, these forces must be equal, i.e.

qQ ^mq^a = C^R ^a

or

ma = ^ .                           (8)

^q      c²R                                                   ' '

Consider the coefficient в of proportionality between gravitational mass and inertial mass. Then

q = mqe ,	(9)
Q = т т в.	(10)
From (8, 9, 10) we get:
e2mqmQ mq =    c t r  ,	(11)
в=c| Q .	(12)
For example, for the Earth we have:
Q « 6 • 1024 кг, R « 6 • 107 м, с « 3 • 109 м/с .
Then

7-24

в = с IR^ 3 • 109 • 10~ « 1. (13)

Thus, our analogy does not contradict the principle of equivalence of gravitational and inertial masses . And we have shown above that in some particular case Mach's principle is fulfilled: the inertial mass is determined by the gravitational mass and the size of the Earth. Formula (12) makes it possible to establish the dependence of the inert mass of a particular body on the parameters of external bodies and thereby determine the nature of this dependence and the limits of applicability of the Mach principle.

Thus, the foregoing shows that Mach's principle can be verified experimentally and, at the same time, the principle of equivalence of inertial and gravitational masses can be verified experimentally.

Application

Let the vector n in the Cartesian coordinate system be directed along the oz axis, and the vector a directed along the ox axis, as shown in Fig. 1. Then we write these vectors in the following form:

n = [0,0, -1],

a = [a%, 0,0]

and find

[n x a] = [0, ax, 0],

[n x [n x a]] = [[0,0, -1] x [0, ax, 0]] = [-ax, 0,0]. Consequently,

Ео = [n x [n x a]] = -a.