Точное квадратичное полиномиальное решение для описания неоднородного течения Куэтта–Пуазейля в бесконечном горизонтальном слое с проницаемыми границами

Исследование ламинарных течений вязкой несжимаемой жидкости между параллельными пластинами служит классической моделью для изучения фундаментальных закономерностей гидродинамики. Такие эталонные решения, как течение Куэтта (сдвиговое течение, вызванное движением стенки) и течение Пуазейля (напорное течение, обусловленное градиентом давления) [1, 2], на протяжении более века используются для верификации численных методов и построения более сложных моделей.

Однако в реальных технических и природных системах границы потока часто являются проницаемыми [3–7]. В таких приложениях, как системы охлаждения с пористыми элементами, мик-рофлюидные устройства для разделения компонентов или процессы фильтрации, сквозной поток через стенки играет ключевую роль в формировании структуры течения. Учет проницаемости качественно меняет картину течения: в отличие от чисто вязкого механизма переноса, характерного для непроницаемых каналов, нормальный поток вносит конвективную составляющую. Это приводит к формированию тонких пограничных слоёв, резкой неоднородности полей скорости и открывает возможности для управления течением, что широко используется в технологиях активного контроля пограничного слоя и тепломассообмена.

Большинство существующих моделей течений в каналах с проницаемыми стенками опирается на простые граничные условия прилипания, что ограничивает их применимость случаями, когда граница движется как единое целое [3, 8]. В то же время, на практике часто возникают ситуации, требующие учета неоднородности профиля скорости на границе, например, при сопряжении с внешним потоком, имеющим поперечные градиенты, или при локальном изменении свойств поверхности.

Механика

В настоящей работе предлагается обобщенная постановка задачи, в которой на верхней проницаемой границе задаются не только значение скорости, но и её первые два пространственных градиента [9–12]. Такой подход позволяет моделировать течения с локальной неоднородностью, не усложняя геометрию расчетной области. Нижняя стенка считается неподвижной и непроницаемой (условие прилипания). Модель учитывает постоянный градиент давления произвольного знака и равномерный нормальный поток (инжекцию или отсос) через обе стенки.

Целью работы является получение точного аналитического решения сформулированной краевой задачи, выявление определяющих безразмерных параметров и анализ структуры течения. Особое внимание уделено асимптотическому поведению решения и количественной оценке толщины пограничного слоя при интенсивной инжекции.

Актуальность исследования обусловлена его приложениями в области микрофлюидики и теплообмена. Например, в биохимических анализаторах с полупроницаемыми мембранами или в системах охлаждения турбинных лопаток с пористыми покрытиями гидродинамическое поле существенно зависит от сквозного потока, и классические модели оказываются неприменимы.

Таким образом, вклад данной работы заключается в построении замкнутого аналитического решения для обобщенной модели течения с проницаемыми границами, учитывающей неоднородные кинематические условия и градиент давления. В отличие от большинства известных решений, ограниченных однородными граничными условиями, предложенная постановка охватывает более широкий класс практических задач. На основе решения строго выводятся ключевые безразмерные параметры подобия: число Рейнольдса Re, число Рейнольдса проницаемости Re w и безразмерный градиент давления S . Это позволяет провести универсальный анализ перехода от вязко-доминированного к конвективно-доминированному режиму течения. Полученные результаты могут служить как для верификации численных методов, так и для проектирования технических систем с управляемыми проницаемыми поверхностями.

Постановка задачи и аналитическое решение

Рассматривается установившееся (стационарное) течение ньютоновской несжимаемой жидкости в плоском канале, образованном двумя бесконечными параллельными пластинами, расположенными на фиксированном расстоянии h друг от друга (рис. 1) [13, 14]. Пластины обладают свойством проницаемости, что означает возможность сквозного прохождения жидкости через них в направлении, нормальном к их поверхности. Такая постановка широко используется в теории течений с инжекцией или отсосом и находит применение в задачах охлаждения пористых поверхностей, микрофлюидики и фильтрации.

-0.2

Нижняя проницаемая пластина (z = 0)

Координата х, м

Рис. 1. Схема течения с проницаемыми границами

Проницаемость Vw (инжекция)

Вдоль канала, то есть в направлении оси x , поддерживается постоянный градиент давления. Это означает, что давление p является линейной функцией координаты x :

dp _{= G ,} dx

где G – заданная константа, имеющая размерность паскаль на метр (Па/м). Важно подчеркнуть, что знак величины G не фиксирован априори. Если G < 0, то давление убывает вдоль направления течения, что соответствует благоприятному градиенту давления и способствует ускорению потока. Если же G > 0, то давление возрастает вдоль течения – это неблагоприятный градиент, который может приводить к замедлению потока, образованию зон обратного течения или даже к

Губарева К.В., Просвиряков Е.Ю.,                Точное квадратичное полиномиальное решение

Еремин А.В.                        для описания неоднородного течения Куэтта–Пуазейля… отрыву пограничного слоя при достаточной интенсивности. Случай G = 0 соответствует отсутствию перепада давления, и движение обусловлено исключительно движением границ и прони- цаемостью.

Выбор системы координат осуществляется следующим образом: ось x направлена вдоль пластин, совпадая с основным направлением течения; ось z направлена перпендикулярно пластинам, причем нижняя пластина расположена в плоскости z = 0, а верхняя – в плоскости z = h . Ось y вводится для описания возможной слабой пространственной неоднородности течения вдоль канала; в рамках данного анализа она рассматривается как поперечная координата, отсчитываемая от некоторого фиксированного продольного сечения. Таким образом, течение считается двумерным в плоскости ( x , z ), но продольная компонента скорости может иметь слабую зависимость от координаты y .

Предполагается, что нормальная компонента скорости постоянна по всему объему:

Vz = Vw = const,(2)

где V w – скорость проницаемости, имеющая размерность м/с. Положительное значение V w > 0 соответствует инжекции (втеканию жидкости в канал через обе пластины), отрицательное V w < 0 – отсосу (вытеканию жидкости из канала). Поперечная компонента скорости отсутствует:

Vy = 0.(3)

Продольная компонента скорости Vx представляется в виде разложения по степеням коорди- наты y до второго порядка включительно:

Vx = U ( z) + yu1( z) + 2- u 2(z).(4)

Такая форма разложения является естественным обобщением одномерного профиля и позволяет учесть линейные и квадратичные градиенты скорости вдоль канала. Функции U ( z ), u 1 ( z ) и u 2 ( z ) являются неизвестными и подлежат определению из уравнений движения и граничных условий. Размерности этих функций следующие: [ U ] = м/с, [ u 1 ] = с^-1, [ u 2 ] = м^-1 ⋅ с^-1, что обеспечивает корректную размерность всех слагаемых в правой части уравнения (4).

Граничные условия формулируются на основе физической постановки задачи. На нижней пластине ( z = 0) предполагается, что жидкость полностью прилипает к неподвижной стенке. Это классическое условие прилипания ( no-slip condition ) означает, что продольная скорость обращается в нуль для любого значения y . Подстановка z = 0 в (4) и приравнивание нулю коэффициентов при всех степенях y дает:

U (0) = 0, u 1 (0) = 0, u 2 (0) = 0.                                    (5)

На верхней пластине (z = h) задается конкретный профиль скорости, который не обязательно соответствует простому условию прилипания. Вместо этого предписываются значения самой скорости и ее первых двух градиентов по y. Это может моделировать, например, сопряжение с внешним течением, имеющим ненулевые поперечные градиенты, или движение стенки с пространственно изменяющейся скоростью. Математически это выражается в виде:

U ( h ) = W , u 1 ( h ) = A , u 2 ( h ) = B ,                                 (6)

где W – характерная скорость (м/с), A – параметр линейного градиента (с^-1), B – параметр квадратичного градиента (м^-1·с^-1). В частном случае A = 0, B = 0 эти условия сводятся к классическому прилипанию на движущейся стенке со скоростью W .

Уравнение неразрывности для несжимаемой жидкости имеет вид:

д V ^д V y   д V ~

—x + —- + —— = 0.

• д x    д y    д z

  Подстановка предположений (2)–(4) в это уравнение показывает, что ∂ V z /∂ z = 0 (поскольку V z = const), ∂ V y /∂ y = 0 (поскольку V y = 0), и ∂ V x /∂ x = 0 (поскольку в разложении (4) явная зависимость от x отсутствует, а y рассматривается как локальный параметр). Следовательно, уравнение неразрывности выполняется тождественно во всем объеме канала.

  Уравнение движения вдоль оси x для стационарного течения вязкой несжимаемой жидкости (уравнение Навье–Стокса без временной производной) записывается как [15, 16]:

  
  

  Г dV dV dV 'V           V

  ^p x        y

  { дx      д y      дz

  
  

  \

  
  

  /

  
  

  д p

  + и д x

  
  

  ( д ² V_X д ² V_X д ² V_X 1 —2 x +— 2r +—2 x _ч дx² дy² дz² _?

  
  

  .

  
  
  
  

Механика

С учетом предположений (2)–(4) и того, что ∂ V x /∂ x = 0, V y = 0, уравнение (8) существенно упрощается. Левая часть (инерционные члены) сводится к одному слагаемому:

dVdV pVz -x- — pVw -x-,(9)

dz поскольку Vx зависит от z только через функции U(z), u1(z), u2(z). Правая часть уравнения (8) также упрощается: вторая производная по x равна нулю, а производные по y и z легко вычисляются из разложения (4):

-x- — u 2( z), —x = U \ z) + yu‘( z) + y-u 2( z),(10)

dy2           dz22

где штрихи обозначают дифференцирование по z . Градиент давления задан соотношением (1),

поэтому -∂ p /∂ x = - G .

Подставляя (9) и (10) в (8), получаем:

P V w

(                  У ²       ^

U '( ^z ) + yu ’ ^{( z} ) + u 2 ^{( z} )

—1

(            У ²

G + p U + yu ‘ +—~ u 2 + u 2

,.

Поскольку это равенство должно выполняться для любого y, приравняем коэффициенты при одинаковых степенях y в левой и правой частях. Приравнивая коэффициенты при y ⁰, y ¹ и y ², получаем систему из трех независимых обыкновенных дифференциальных уравнений:

при y ⁰:

ρVwU′ = -G + μ(U′′+u2);(12)

при y ¹:

ρVwu1′ = μu1′′;(13)

при y ²:

ρVwu2′ = μu2′′.(14)

Эта система, дополненная граничными условиями (5) и (6), полностью определяет искомые функции U ( z ), u 1 ( z ) и u 2 ( z ). Уравнения (13) и (14) являются линейными однородными уравнениями второго порядка с постоянными коэффициентами и имеют идентичную структуру. Уравнение (12) является линейным неоднородным, причем его правая часть зависит от функции u ₂( z ), которая находится из уравнения (14).

Перейдем к решению системы уравнений (12)–(14) в безразмерной форме [17, 18]. Целью такого перехода является выявление основных физических параметров, определяющих структуру течения, и приведение задачи к универсальному виду, не зависящему от конкретных размерных величин. Для этого вводится набор характерных масштабов, основанных на геометрии канала и кинематических условиях на верхней стенке.

В качестве масштаба длины выбирается расстояние между пластинами h , в качестве масштаба скорости – величина W , заданная в граничном условии (6). Масштаб давления естественным образом определяется из вязкого члена в уравнении Навье–Стокса и равен μW / h . На основе этих масштабов вводятся следующие безразмерные переменные:

z _ɶ U       u ₁ h

Z , U , u i , u?

h ^, W ^{,   1}    W ^{, 2}

u ₂ h ² W

.

Безразмерная координата ζ изменяется в интервале от 0 до 1, что соответствует нижней и верхней пластинам соответственно. Введенные безразмерные функции U(Z), u(Z), u2(Z) теперь являются величинами порядка единицы, что удобно для численного анализа и физической интерпретации.

Переход к безразмерным переменным в уравнениях (13) и (14) требует замены производных. Поскольку d / d z = (1/ h ) d / d Z, то u i' = ( W /( h‘ )) й ‘/ h = ( W /( h‘ + 1 )) й ‘ и u i" = ( W /( h‘ + ²)) й " , где штрихи в правой части обозначают дифференцирование по ζ . Подстановка этих соотношений в уравнения (13) и (14) и сокращение общих множителей приводит к одинаковой безразмерной форме для обоих уравнений:

й ''— Re w H ' , i — 1,2, (16) где введено безразмерное число, играющее ключевую роль в задачах с проницаемыми границами. Это число Рейнольдса, основанное на скорости проницаемости:

Губарева К.В., Просвиряков Е.Ю.,                Точное квадратичное полиномиальное решение

Еремин А.В.                        для описания неоднородного течения Куэтта–Пуазейля…

Re w = V w h , v = ^ .                                (17)

v P

Здесь ν – кинематическая вязкость жидкости (м² /с), а Re _w физически представляет собой отношение конвективного переноса импульса, обусловленного нормальным потоком через стенки, к диффузионному переносу, обусловленному вязкостью. При Re _w ≪ 1 вязкие силы доминируют, и течение распределено по всему сечению канала. При | Re _w | ≫ 1 конвективный перенос локализует течение в тонких слоях вблизи границ.

Граничные условия (5) и (6) в безразмерной форме принимают следующий вид. На нижней стенке ( ζ = 0):

Ui(0) = 0, ^(0) = 0, й2(0) = 0.(18)

На верхней стенке (ζ = 1) вводятся безразмерные параметры, характеризующие заданные градиенты скорости:

Ahbh

a = —, b =

WW что позволяет записать условия как:

U(1) = 1, ^(1) = a, й2(1) = b.(20)

Параметры a и b являются безразмерными и описывают относительную интенсивность линейного и квадратичного градиентов скорости по сравнению с основной скоростью W .

Рассмотрим теперь решение уравнения (16). Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. его характеристическое уравнение имеет корни r = 0 и r = Re _w , поэтому общее решение записывается в виде:

йi (Z) = Ci + DieRew Z,(21)

где C i и D i – константы интегрирования, подлежащие определению из граничных условий (18) и (20).

Применяя условие й i (0) = 0 , получаем:

Ci = -Di.(22)

Подстановка этого результата в (21) дает:

й (Z) = Di (eRew Z -1).(23)

Далее, используя условие на верхней стенке u ɶ _i (1) = K i , где K 1 = a и K 2 = b , находим:

D = —Ki— i    e ^Re w - 1

Окончательно, подставляя (24) в (23), получаем явные выражения для безразмерных профилей:

R ^Re w ^Z _ 1

U1 Z ) = a _Re ,                                    (25)

e ^Re w - 1

e ^Re w Z _1

U2 Z ) = b _Re ,                                    (26)

e ^Re w - 1

Эти формулы представляют собой точные аналитические решения для коэффициентов разложения продольной скорости. Их структура – экспоненциальная, что является прямым следствием наличия нормального потока через проницаемые границы. В пределе Rew → 0 с использованием разложения ex ~ 1 + x эти выражения переходят в линейные зависимости йi(Z) = KiZ, что соответствует классическому случаю отсутствия проницаемости. При больших положительных значениях Rew профили становятся резко неоднородными, концентрируясь вблизи верхней стенки.

Для приведения уравнения (12) к безразмерному виду необходимо ввести еще один ключевой безразмерный параметр, характеризующий влияние перепада давления. Из уравнения (12): ρ V w U ′ = - G + μ ( U ′′ + u 2 ),

Механика выразим все члены через безразмерные переменные (15). Учитывая, что U' = (W1 h) U' и U” = (W1 h2) й”, а также подставляя и2 = (W/h2) й2, получаем после деления всего уравнения на

μ W / h ²:

p V w h Р

и ' = - ^Gh + й " + и p W

Первый коэффициент в левой части является числом Re _w , определенным в (17). Второй коэффициент в правой части – это безразмерный градиент давления, который удобно определить со знаком «минус», чтобы положительное значение параметра соответствовало движению, вызванному падением давления вдоль течения. Таким образом, вводим:

S = — (- G )• p W

Этот параметр S является безразмерным и может принимать любые вещественные значения. При G < 0 (давление падает вдоль x ) имеем S > 0; при G > 0 (давление растет) – S < 0; при отсутствии градиента давления ( G = 0) – S = 0. С учетом этого определения безразмерная форма уравнения (12) принимает окончательный вид:

U "-Re w U ' = - S - ^( Z ) .

Правая часть этого уравнения полностью определена, поскольку функция uɶ2 (ζ) уже найдена и задается формулой (26). Для упрощения записи введем вспомогательную константу:

C =__ b__ e ^Re w - 1

что позволяет переписать (26) в компактной форме:

H 2 ( C ) = C ( e ^Re w ^Z - 1).

Подстановка (30) в правую часть уравнения (28) дает:

-S - u2 (Z) = -S - CeRew Z + C = -(S - C)- CeRewZ.

Таким образом, уравнение (28) представляет собой линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами и правой частью, состоящей из константы и экспоненциальной функции. Его общее решение строится как сумма общего решения однородного уравнения и частного решения неоднородного.

Однородное уравнение, соответствующее (28), имеет вид й ” - Re w й ' = 0 и, как и ранее, имеет общее решение:

U h ( Z ) = D 1 + D 2 e ^Re w ^Z ,                                  (32)

где D 1 и D 2 – новые константы интегрирования.

Для нахождения частного решения й p (Z) воспользуемся методом неопределенных коэффи- циентов [19]. Правая часть (31) состоит из двух слагаемых: константы - (S - C) и экспоненты -CeRewZ . Для константного слагаемого частное решение ищем в виде линейной функции aZ, поскольку константа является решением однородного уравнения (корень r = 0). Подстановка αζ в левую часть (28) дает -Rew α, что должно равняться - (S - C). Отсюда:

S - C а =------.

Re w

Для экспоненциального слагаемого -C eRewZ стандартный анзац в eRew Z не подходит, так как eRewZ также является решением однородного уравнения (корень r = Rew). В этом случае частное решение следует искать в виде eZeRewZ . Вычислим его производные:

-d - ( eZ e ^Re w ^Z ) = e e Re w ^Z + в Re w Z e Re w ^Z ,

Z ( вZ e ^Re w ^Z ) = 2 в Re w e ^Re w ^Z + в Re w² Z e Re w ^Z

.

Подстановка в левую часть (28):

[2 в Re w e ^Re w ^Z + в Re w² Ze Re w ^Z ] - Re w [ в Re w ^Z + в Re w Ze Re w ^Z ] = в Re w e Re w ^Z Это должно равняться - C e ^Re w ^Z , откуда:

.

в Re w = - C , в = - C—

Re _w

.

Собирая оба вклада, получаем частное решение:

U_p ( Z ) = SC Z - — Z e ^Re w ^{Z p}      Re w    Re w

.

Полное общее решение уравнения (28) есть сумма (32) и (35):

U ( Z ) = D i + D₂e Re w ^Z + SC Z —— Z e ^Re w ^{Z 1    2}        Re w     Re w

.

Теперь необходимо определить константы D 1 и D 2 из граничных условий (18) и (20) для

ɶ

ɶ

функции U . Первое условие U (0) = 0 дает:

D 1 = - D 2 .

Подставим это соотношение в (36):

U ( Z ) = D ₂( e ^Re w ^Z

1) + S— C Z — — Z e ^Re w ^Z

Re w    Re w

.

Второе граничное условие U ( 1 ) = 1 приводит к уравнению:

1 = D ₂( e ^Re w

S - C C _Re

1) +--- e ^Re w

Re w  Re w

.

Решая это уравнение относительно D 2 , получаем:

1 -

D 2 =

S - C C Re , S C / Re П -----+---- e ^Re w 1 +----+----( e ^Re w -1)

Re w  Re w          Re w  Re w

e ^Re w - 1

e ^Re w - 1

.

Вспоминая определение константы C из (29), замечаем, что C ( e ^{Re w} существенно упростить выражение (40):

-

1) = b . Это позволяет

D 2 =

, S b , S + b

1 +----+---- 1 +-----

Re w  Re w      Re w

e ^Re w - 1

e ^Re w - 1

.

Соответственно, из (37):

, S + b

1 +-----

D =__ ^Re w

.

¹    e ^Re w - 1

Таким образом, функция U ( Z ) полностью определена формулами (36), (41) и (42). В совокупности с (25) и (26) это завершает построение полного аналитического решения задачи в безразмерной форме.

Проведем анализ полученного решения в предельных случаях. Начнем с предела малых чисел Рейнольдса, Re _w →0, который соответствует ситуации слабой проницаемости или высокой вязкости [20, 21]. В этом случае все экспоненциальные функции раскладываются в ряд Тейлора:

e ^Re w ^Z = i ₊ Re z + w

(Re w Z ) 2 + (Re w Z )

e ^Re w - 1 = Re w +

Re ² Re ³ w + w

~ + O (Re w ⁴),

+ O (Re w 4 ).

Механика

U 2 ( Z ) = b Z + R/ ( z ² - Z ) + O (Re w ²)

Подстановка этих разложений в (25) и (26) с точностью до первого порядка по Re _w дает:

U ( Z ) = a Z + Re w ( Z 2 - Z ) + о (Re w 2) _        2                             _

,                              (43)

Для основного профиля UJ (Z) в пределе Rew ^0 уравнение (28) переходит в уравнение Пуа- зейля с дополнительным источником:

U0(Z) = -S -bZ.(45)

Двукратное интегрирование этого уравнения с учетом граничных условий U о ( 0 ) = 0, U о ( 1 ) = 1 приводит к полиномиальному решению третьей степени:

U0 (Z ) = [1 + S+b 1Z - S Z2 - b Z3.(46)

Z 2 2 J 26

Этот результат полностью согласуется с классической теорией течения Куэтта–Пуазейля, обобщенной на случай квадратичной неоднородности на верхней стенке.

Теперь рассмотрим противоположный предел больших положительных чисел Рейнольдса [22, 23], Rew → +∞, который описывает режим сильной инжекции. В этом случае eRew ≫ 1 , и для ζ < 1 справедливо приближение:

e Re w Z - 1 e Re w Z e ^Re w - 1     e ^Re w

_ - Re w (1 - Z )

= e .

Следовательно, профили (25) и (26) приобретают вид:

U 1 ( Z ) * ae ^{- Re} w ^{(1 - Z} ) , й₂ ( Z ) = be ^- R ^e w ^{(1 - Z} ) •

Эти функции экспоненциально малы во всем объеме канала, за исключением тонкой области вблизи верхней стенки, где 1- ζ = O(1/ Re _w ). Аналогичное поведение демонстрирует и профиль U ( Z ) , который стремится к нулю при Z < 1 и быстро нарастает до единицы вблизи Z = 1.

Характерная толщина области, в которой происходит этот резкий переход, определяется из условия, что аргумент экспоненты в (47) имеет порядок единицы:

Re w (1- ζ ) = O (1).                                   (49)

Переходя к размерным переменным с помощью ζ = z / h , получаем:

h — z

Re _w — = O (1), h - z = O h

< А ih-

Z ^Re w J

.

Таким образом, толщина пограничного слоя у верхней стенки оценивается как:

h

.

О ~---

Re w

Эта оценка является прямым следствием структуры точного аналитического решения и не требует дополнительных гипотез. Она справедлива при Rew ≫ 1 и описывает локализацию тече- ния в тонком слое у верхней пластины в случае инжекции (Vw > 0). В случае отсоса (Vw < 0, Rew → -∞) аналогичный пограничный слой формируется у нижней стенки, и его толщина также оценивается как δ∼h/∣ Rew ∣.

Полученное решение является строгим аналитическим результатом для поставленной краевой задачи с учетом постоянного градиента давления произвольного знака, проницаемости границ и неоднородных кинематических условий на верхней стенке. Оно применимо для анализа течений в каналах с проницаемыми поверхностями, возникающих в задачах фильтрации, теплообмена и микрофлюидики.

Методика численного моделирования

Численное моделирование выполнено на основе полученного аналитического решения [24, 25]. Для верификации решения и визуализации пространственной структуры течения проведены расчеты для трех реальных ньютоновских жидкостей: воды, глицерина и этиленгликоля при температуре 20 °C. Физические свойства жидкостей (плотность ρ и динамическая вязкость μ ) взяты из справочных данных.

Геометрические и кинематические параметры задачи зафиксированы следующим образом: расстояние между пластинами h = 10 мм, скорость верхней стенки W = 0,5 см/с, параметры градиента скорости A = 0,1 с^-1 и B = 0,002 м^-1·с^-1, скорость проницаемости V w = 0,2 см/с (инжекция), градиент давления G = –5 Па/м.

Расчетная область дискретизирована с использованием неравномерной сетки по координате z , сгущенной вблизи верхней стенки ( z = h ) для точного разрешения тонкого пограничного слоя при больших значениях Re_w . По координате y использована равномерная сетка на интервале [-10, 10] см. Для каждой жидкости вычисляются безразмерные параметры Re = Wh /ν, Re_w = V w h /ν, a = Ah / W , b = Bh ²/ W и S = h ²(- G )/(μ W ).

Поле продольной скорости V x ( y , z ) вычисляется по формуле (4) с подстановкой аналитических выражений для U (z), u 1 ( z ) и u 2 ( z ). На основе этого поля численно определяются производные ∂ V x /∂ z и ∂ V x /∂ y с использованием центральных разностей второго порядка точности, что позволяет рассчитать поля завихренности и напряжений сдвига. Все вычисления выполнены в среде MATLAB R2023b с двойной точностью. Для предотвращения численной неустойчивости при ∣ Re_w ∣ < 10^-12 используется предельный полиномиальный вариант решения (46) [26].

Результаты и их обсуждение

Для верификации полученного аналитического решения и исследования влияния физических свойств жидкости на структуру течения был проведен расчетный эксперимент. Результаты демонстрируют качественно различное поведение течения в зависимости от соотношения между вязкостью жидкости и интенсивностью проницаемости.

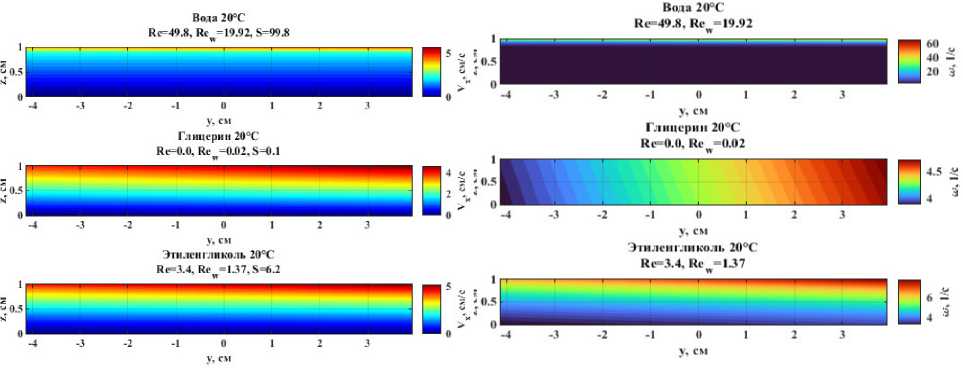
Рис. 2. Поля продольной компоненты          Рис. 3. Поля завихренности ω для различных скорости Vx для различных жидкостей                       жидкостей

На рис. 2 представлены поля продольной компоненты скорости V x для всех трех жидкостей. Несмотря на идентичные граничные условия и геометрию, профили существенно различаются. Вода, обладающая наименьшей вязкостью, демонстрирует наиболее выраженную неоднородность вблизи верхней стенки, что является следствием высокого значения Re_w = 19,92. Напротив, глицерин с его высокой вязкостью ( μ = 1,49 Па·с) характеризуется почти линейным профилем скорости по всему сечению канала ( Re_w = 0,027), что указывает на доминирование вязких сил. Этиленгликоль занимает промежуточное положение. Полученные результаты находятся в качественном соответствии с выводами асимптотического анализа.

Структура течения более полно раскрывается при анализе поля завихренности ω = ∂ Vx /∂ z , представленного на рис. 3. Для воды наблюдается резкий пик завихренности в тонком слое у

Механика верхней стенки, что подтверждает наличие конвективно-доминированного пограничного слоя. У глицерина распределение завихренности практически однородно, что типично для течений, управляемых вязкостью. Этиленгликоль вновь демонстрирует переходный характер. Сравнение этих полей с профилями скорости позволяет сделать вывод о том, что именно градиент скорости, а не ее абсолютное значение, определяет локальную динамику вязкого трения.

Этот вывод подтверждается и распределением напряжений сдвига τ = μ ∂ V x /∂ z , показанным на рис. 4. Несмотря на то, что градиент скорости у воды максимален, ее низкая вязкость приводит к умеренным напряжениям. В то же время, глицерин, несмотря на малый градиент скорости, создает значительно более высокие напряжения сдвига из-за своей высокой вязкости. Это подчеркивает важность комплексного учета обоих факторов: как кинематики течения, так и реологических свойств жидкости – при оценке сил трения в каналах с проницаемыми стенками.

Полная картина течения, включающая вклад нормальной компоненты скорости V z = V w , отражена в модулях полной скорости ∣ V ∣ , изображенных на рис. 5. Видно, что для всех жидкостей

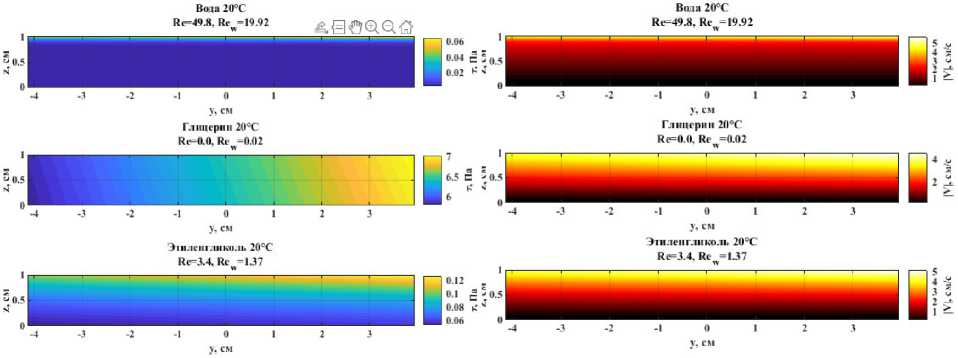
Рис. 5. Поля модулей полной скорости ∣ V ∣ для различных жидкостей

Рис. 4. Поля напряжений сдвига τ для различных жидкостей нормальная компонента вносит заметный вклад, особенно в области, удаленной от верхней стенки. Для воды, где продольная скорость в ядре канала мала, модуль полной скорости определяется в основном проницаемостью, что приводит к почти однородному полю. Для глицерина, напротив, высокая продольная скорость в центре канала доминирует над нормальной компонентой. Это демонстрирует сложное взаимодействие между движением стенки, градиентом давления и проницаемостью.

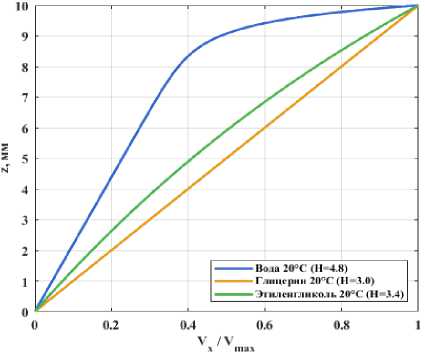
Рис. 6. Профили продольной скорости V x ( y = 0) для различных жидкостей

Для количественного сравнения профилей на рис. 6 приведены зависимости продольной скорости Vx от координаты z в центральном сечении канала (y = 0). Четко видна тенденция: с увеличением числа Рейнольдса Re профиль становится все более «наполненным», стремясь к равномерному распре- делению. Глицерин (Re = 0,034) имеет почти треугольный профиль, характерный для чистого течения Куэтта, в то время как вода (Re = 49,8) демонстрирует почти плоский профиль в ядре потока с резким падением до нуля у нижней стенки. Этот переход от вязко-доминированного к конвективно-доминированному режиму является основной особенностью исследуемой задачи.

Обобщенная картина режимов течения представлена на карте режимов на рис. 7, где по осям отложены числа Рейнольдса Re и Rew [29, 30]. Жидкости маркированы в соответствии с их физическими свойствами. Карта наглядно демонстрирует, что глицерин находится в области ламинарного, диффузионно-доминированного течения, в то время как вода расположена в зоне лами- нарного, но конвективно-доминированного режима. Эта визуализация подтверждает, что для полного описания течения в каналах с проницаемыми стенками недостаточно одного числа Рейнольдса; необходимо учитывать и число Rew, характеризующее интенсивность проницаемости.

Для более глубокого анализа структуры пограничного слоя были рассчитаны его интегральные характеристики: толщина вытеснения δ * и толщина импульса θ . На рис. 8, а ) (слева) показаны нормированные профили скорости, а на рис. 8, б ) (справа) – соответствующие интегральные толщины. Форма профиля для глицерина близка к линейной, что дает высокое значение формы H = δ */ θ ≈ 2,5, характерное для ламинарных течений с малым градиентом давления. Профиль для воды значительно более «наполненный», что приводит к снижению H до значения около 1,2, что типично для те-

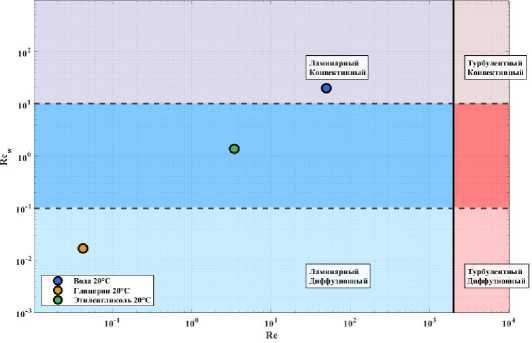
Рис. 7. Карта режимов течения в координатах Re и Re w

чений с благоприятным градиентом давления или сильной инжекцией.

Особое внимание было уделено верификации асимптотической оценки толщины пограничного слоя δ ∼ h /Re w . На рис. 9 представлены результаты специализированного анализа для воды

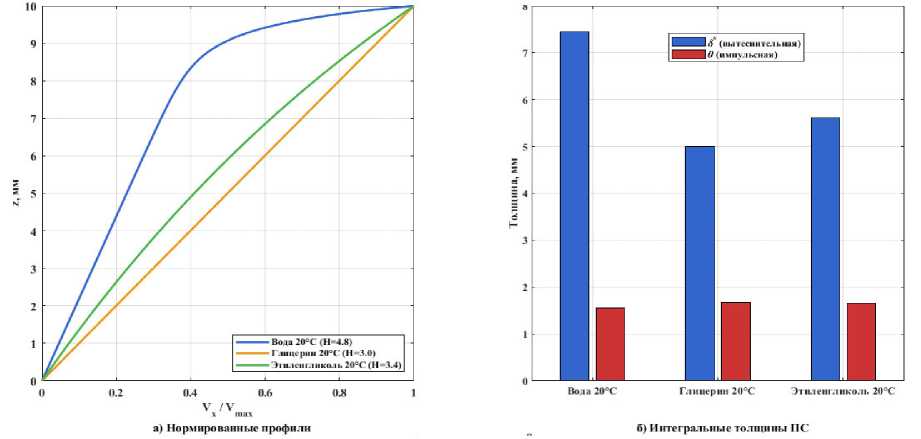
Рис. 8. Нормированные профили скорости и интегральные толщины пограничного слоя для различных жидкостей

при различных значениях Re w . На рис. 9, а видно, как с ростом Re w профиль скорости все более локализуется вблизи верхней стенки. Рис. 9, б показывает, что численно определенная толщина слоя δ 99 (расстояние, на котором скорость достигает 99 % своего максимума) с высокой точностью следует асимптотической зависимости δ = 1/Re w . Рис. 9, в демонстрирует, что относительная ошибка этой оценки стремится к нулю при Re w → ∞, что является прямым подтверждением корректности проведенного асимптотического анализа.

Таким образом, проведенный численный эксперимент полностью подтверждает все ключевые положения аналитического решения [27, 28]. Полученные результаты демонстрируют, что структура течения в каналах с проницаемыми стенками определяется не только вязкостью и скоростью движения границ, но и интенсивностью нормального потока, которая контролирует локализацию течения. Введение числа Рейнольдса Re w , основанного на скорости проницаемости, оказывается необходимым для описания перехода от диффузионного к конвективному режиму. Эти выводы имеют важное значение для прикладных задач в области микрофлюидики, фильтрации и

Механика тепломассообмена, где управление течением через проницаемые поверхности является ключевым технологическим приемом.

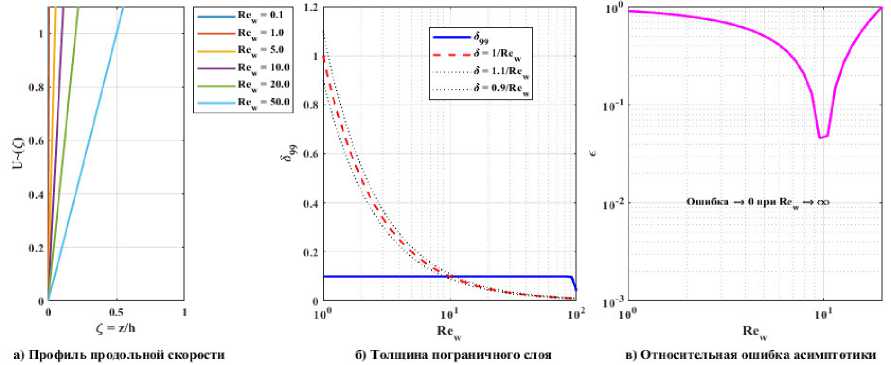
Рис. 9. Анализ пограничного слоя для воды: профили скорости, толщина слоя и относительная ошибка асимптотики

Заключение

В настоящей работе предложена и исследована модель установившегося течения вязкой несжимаемой жидкости в плоском канале с проницаемыми стенками, учитывающая одновременное влияние движения границ, нормального сквозного потока и постоянного градиента давления. В отличие от классических постановок, на верхней границе задан не только профиль скорости, но и его первые два пространственных градиента, что позволяет описывать более широкий класс практических течений, включая сопряжение с внешними потоками или локальные неоднородности.

Аналитическое решение задачи получено в замкнутой форме и выражено через три безразмерных параметра: число Рейнольдса Re, число Рейнольдса на основе скорости проницаемости Re w и безразмерный градиент давления S . Такая параметризация позволяет единообразно описывать как вязко-доминированные, так и конвективно-доминированные режимы. Особое внимание уделено асимптотическому поведению решения: в пределе слабой проницаемости восстанавливается полиномиальный профиль, характерный для обобщенного течения Куэтта–Пуазейля, тогда как при сильной инжекции течение локализуется в тонком пограничном слое у верхней стенки.

На основе структуры точного решения строго выведена оценка толщины этого слоя, пропорциональная h /Re w , что подтверждено численным анализом для реальных жидкостей. Полученные результаты демонстрируют, что для адекватного описания течений в каналах с проницаемыми поверхностями недостаточно традиционного числа Рейнольдса; необходимо дополнительно учитывать интенсивность нормального потока через параметр Re w . Данная модель может служить теоретической основой для проектирования и оптимизации технических систем, где управление течением осуществляется именно через проницаемые границы.