Точное оценивание линейных регрессионных моделей методом наименьших модулей на основе спуска по узловым прямым
Бесплатный доступ
При построении линейных моделей во многих случаях приходится сталкиваться со стохастической неоднородностью экспериментальных данных. Это проявляется в нарушении условий теоремы Гаусса-Маркова, в частности наблюдения могут быть засорены грубыми ошибками. В этих условиях оценивание параметров моделей требуется выполнять с помощью устойчивых методов. К их числу относят метод наименьших модулей. Однако известные алгоритмы его реализации являются достаточно эффективными лишь для малых размерностей моделей и ограниченного объема выборок. Цель данного исследования - разработка эффективных вычислительных алгоритмов реализации метода наименьших модулей, не имеющих ограничений на порядок моделей и объем экспериментальных данных. Описаны алгоритмы точного решения задачи оценивания параметров линейных регрессионных моделей методом наименьших модулей. Они основаны на спуске по узловым прямым. Для снижения вычислительных затрат использована особенность узловых прямых - все расположенные на каждой такой прямой узловые точки являются пересечением набора гиперплоскостей, из которых различными является только одна гиперплоскость. Данные алгоритмы значительно выигрывают по сравнению с известным переборным алгоритмом и могут эффективно использоваться на практике. Получена оценка вычислительной сложности алгоритма спуска по узловым прямым. Приведена схема алгоритма.
Метод наименьших модулей, линейная регрессионная модель, алгоритм, узловая точка, узловая прямая, гиперплоскость, вычислительная сложность
Короткий адрес: https://sciup.org/147158976
IDR: 147158976 | УДК: 519.237.5:519.24 | DOI: 10.14529/mmph180205
Текст научной статьи Точное оценивание линейных регрессионных моделей методом наименьших модулей на основе спуска по узловым прямым
Одной из распространенных задач при статистической обработке результатов экспериментальных исследований является оценивание неизвестных коэффициентов линейной регрессионной модели [1-4]
где у =
А y 1
У 2
V Уп 7
рица; £ =
сии.
е R n
А
Е 1
Е 2
у = Xa + £ ,
( 1
- вектор измерений; X = { x j } п х m =
е R п - вектор случайных ошибок; a =
VЕ n 7
( „ А a 1
a 2
x 12
x 22
xn 2
е R m
Vam 7
-
v A x 1 m
Av А x1
x 2 m
x 2
- заданная мат-
х
nm 7
V x п 7
вектор коэффициентов регрес-
Среди прикладных статистических методов построения регрессионных зависимостей наибольшее распространение получил метод наименьших квадратов (МНК). Использование МНК требует выполнения ряда предпосылок, называемых условиями Гаусса-Маркова [4, с. 6 - 7]. При их выполнении МНК-оценки параметров модели (1) являются состоятельными и несмещенными. Кроме того, если случайные ошибки имеют нормальный закон распределения, то МНК-оценки становятся эффективными. Однако использование МНК при нарушении условий Гаусса– Маркова может привести к значительным ошибкам при оценивании коэффициентов, а в случае присутствия в измерениях больших выбросов даже к несостоятельности оценок.
С целью обеспечения устойчивости оценок относительно отклонений случайных ошибок от гауссовой модели разработан ряд статистических методов, основанных на более общих предположениях относительно случайных ошибок. Одним из них является метод наименьших модулей (МНМ) [5, 6]. МНМ для задачи (1) имеет вид
n
Q ( a )=El yt - (a, x - •) H min • (2)
. ' aeR i=1
Целевая функция Q ( a ) задачи (2) является выпуклой. Поскольку во всех точках, где у функции Q ( a ) существует производная, она линейна, то, следовательно, ее локальные минимумы могут быть только в особых точках. Известно несколько точных и приближенных методов решения задачи (2) [6 - 9].
Кусочно-линейный вид целевой функции позволяет рассчитывать на наличие быстрых и точных методов решения задачи (2). Однако в настоящее время в целом удовлетворительно решена только проблема ее приближенного решения. Здесь можно отметить метод вариационновзвешенных квадратических приближений (называемый также алгоритмом Вейсфельда) [6, 7], подход, основанный на сведении данной проблемы к задаче линейного программирования и ее приближенное решение методом внутренней точки [10], численные методы спуска нулевого порядка [9]. Недостатком этих методов в первую очередь является неточное решение при относительной простоте целевой функции.
К точным методам относится сведение (2) к эквивалентной задаче линейного программирования [6, 11] и ее решение при помощи широко известного симплекс-метода и переборный алгоритм [9].
Использование симплекс-метода ограничено задачами малой размерности. Это вызвано накоплением погрешностей из-за ошибок округлений и требованием чрезмерно большого выделения памяти. Предложенное в [12] использование массивно-параллельных вычислений с использованием дробно-рациональных вычислений без округления устраняет проблему накопления вычислительных погрешностей, но приводит к существенному усложнению реализации и росту вычислительных затрат, затрудняющих широкое практическое применение данного подхода.
Второй метод [9] основан на переборе всех узловых точек, в которых не существует производная функции Q ( a ) ни по одному из возможных направлений пространства R m . Переборный алгоритм требует решения C n m систем линейных уравнений порядка m . Вычислительные погрешности здесь незначительны и не накапливаются. Однако с ростом n и m наблюдается экспоненциальный рост вычислительных затрат. Фактически практическое применение переборного алгоритма ограничено объемом выборки n < 200 и числом коэффициентов регрессии m < 4. Однако отсутствие эффекта накопления вычислительных погрешностей делает возможным использование данного метода при условии ограничения числа перебираемых узловых точек.
Целью статьи является описание эффективного, точного вычислительного метода решения задачи (2), осуществляющего неполный перебор особых точек.
Алгоритмы спуска по узловым прямым
Обычный спуск. Введем гиперплоскости Q, = Q ( a , x, , yz ) в виде уравнений:
-
У, - (a, x^ = 0, (z = 1,2, ..., n).(3)
Зададим также узловые точки пересечения гиперплоскостей (3):
u (k,..., k„) = A Q,, M = {k!,..., km }, k 1 < k 2 < „.< km, kz e {1,2, _, n}.
-
1 ms
Тырсин А.Н., Точное оценивание линейных регрессионных моделей
Азарян А.А. методом наименьших модулей на основе спуска по узловым прямым
Обозначим U - множество всех узловых точек (4). Алгоритм точного решения задачи (2) основан на спуске к точному решению, двигаясь вдоль узловых прямых l , каждая из которых является пересечением ( m — 1) различных гиперплоскостей Q i :
k m — 1
l ( k , k m Щ П Q . • k l 6M - , n}. (5)
i = k i
В качестве начального приближения берется произвольная узловая точка, являющаяся пересечением m гиперплоскостей Q ц ,..., Q к . Исключив одну из гиперплоскостей, получим узловую прямую l . В любой узловой точке можно построить m таких узловых прямых. Выберем ту, вдоль которой целевая функция достигает наименьшего значения, которое всегда будет достигаться в одной из узловых точек. Найдя эту точку, продолжим движение из нее по тому же принципу. В результате будет найдена узловая точка, спуск из которой невозможен. И эта узловая точка будет являться точным решением задачи (2). В основе алгоритма лежат следующие теоремы.
Теорема 1. Рассмотрим модель (1), для которой имеется выборка наблюдений ( x i , y i ) = ( x i 1 , x i 2,..., xim , y i ), ( i = 1, ... , n ), и пусть заданы функция Q ( a ) задачи (2), гиперплоскости (3) и множество U всех узловых точек (4). Тогда функция (2) всегда имеет точку глобального минимума, эта точка либо единственна и принадлежит U , либо состоит из выпуклого линейного многогранника, вершины которого являются точками из U .
Доказательство теоремы 1 . Известно, что выпуклая, непрерывная, кусочно-линейная функция либо имеет глобальный минимум, либо стремится к минус бесконечности. А поскольку функция Q ( а ) является также ограниченной снизу ( Q ( a ) > 0 как сумма модулей) функцией, то она всегда имеет точку глобального минимума.
Пусть а* = (а^,а2,..., a*m)T — стационарная точка и является точкой минимума функции Q(а). Тогда ее градиент в этой точке равен нулю. Поскольку Q(a) кусочно-линейная функция, то из равенства grad Q(а *) = 0 следует, что функция Q(а) является постоянной функцией на выпуклом многограннике с вершинами а1, а2,..., а1, гранями которой являются гиперплоскости (3), имеющем вид [13]:
ll A = { а : а = £ У а k , £ 4 = 1}. k = 1 k = 1
Функция Q ( а ) является постоянной до граничных точек многогранника A , лежащих на гиперплоскостях (3) Следовательно, вершины а 1 , а 2 ,..., а 1 этого многогранника являются узловыми точками и функция Q ( а ) достигает минимума и в этих точках.
Все гиперплоскости (3), и только они являются особыми точками функции Q ( а ), поскольку только в них она не дифференцируема. Если взять m — 1 произвольных невырожденных соотношений вида lt = y i — (а , x^ = 0, то они в совокупности определяют прямую (5) в пространстве
( а 1 , a 2 ,..., a m ) и вместе с тем плоскость P ( Q , k 1 ,..., k m — 1 ) , Па раллельную оси Q в пространстве ( Q , а 1 , а 2,..., a m ). Присоединяя к системе (5) выражение (2) и рассматривая их совместно, найдем уравнение ломанной M , полученной в результате пересечения поверхности (2) плоскостью P ( Q , k 1 ,..., k m — 1 ) .
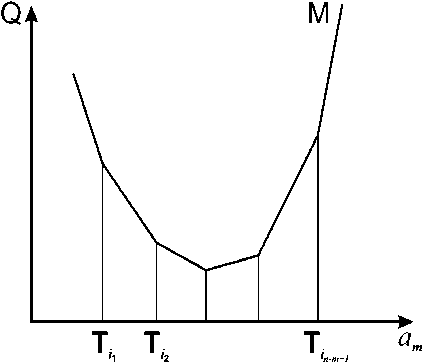
Рис. 1. Вид функции
Если с помощью уравнений, входящих в систему (5), выразить m — 1 неизвестных а 1 , а 2,..., a m — 1 через оставшееся неизвестное и подставить в выражение (2), то получим уравнение проекции ломанной M на плоскость ( Q , a m ) (рис. 1). Точки T,T 2 ,..., T i + 1 являются проекциями на эту плоскость точек пересечения прямой l ( k 1 ,..., km — 1 ) гиперплоскостями (3), не вошедшими в (5).
Функция Q(am) на плоскости (Q, am) - выпуклая и кусочно-линейная c особыми точками T,T2,...,T_m, которые являются узловыми точками. Отсюда следует, что функция Q(а) дости гает минимума в узловой точке.
Теорема 2. Алгоритм спуска вдоль узловых прямых для нахождения решения задачи (2), сходится к точному решению за конечное число шагов.
Доказательство теоремы 2. На каждом шаге алгоритма мы находим узловую точку с все меньшим значением целевой функции, а поскольку количество узловых точек конечно, то алго- ритм выполняется за конечное число шагов.
Докажем, что алгоритм всегда будет достигать минимума целевой функции (т. е. решения). Допустим, что мы находимся на k -м шаге алгоритма в какой-то узловой точке и пытаемся осуществить спуск вдоль одной из m узловых прямых, проходящих через эту точку, к другой узловой точке с меньшим значением целевой функции. Покажем, что либо мы сможем найти такую точку, либо текущая узловая точка является минимальной.
Целевая функция Q ( а ) является выпуклой функцией в пространстве R m . Поэтому, если взять произвольную точку ~ и m линейно независимых прямых "j , ( j = 1,2, . . , m ), проходящих через нее, то либо найдется такая окрестность этой точки, в которой целевая функция будет убывать хотя бы вдоль одного из направлений, либо в текущей узловой точке достигается минимум целевой функции.
Поскольку вероятность того, что случайная величина (случайные погрешности) более одного раза примет одно и то же значение, равна нулю, то узловые прямые, проходящие через узловую точку, являются линейно независимыми. То есть вдоль одной из них целевая функция убывает, причем она будет убывать вплоть до следующей узловой точки на этой узловой прямой, поскольку между двумя соседними узловыми точками, целевая функция (2) будет линейна, так как все ее подмодульные выражения не будут менять знак. Действительно, смена знака означает пересечение одной из образующих гиперплоскостей, что приведет к образованию узловой точки, а мы рассматриваем часть узловой прямой между двумя соседними узловыми точками.
На практике из-за конечной точности измерений гипотетически могут возникнуть ситуации, когда узловые прямые, проходящие через узловую, окажутся параллельными. В этом случае уз- ловой точки не существует, и переходим к рассмотрению другой узловой прямой.
Таким образом, либо произвольная узловая точка является минимумом целевой функции, либо хотя бы по одной из проходящих через нее узловых прямых можно сделать переход к узло- вой точке с меньшим значением целевой функции. Теорема доказана.
Поясним этот алгоритм, используя рис. 1 (для случая m = 2). В качестве начальной точки вы берем точку H. Через нее проходят прямые I и II. Сначала рассмотрим прямую I. Среди узловых точек, которые лежат на этой прямой, выбираем ту, в которой достигается минимальное значение целевой функции (таким образом, происходит спуск по прямой). Предположим, что такой точкой является точка C. Рассмотрим прямую II. Спускаясь по прямой II, находим на ней точку, в которой достигается минимальное значение. Пусть, например, эта точка L. Далее, сравнивая значения целевой функции в точках C и L, выбираем ту, в которой достигается минимальное значение. Пусть, например, эта точка C. Через нее помимо прямой I проходит прямая III. На этой прямой находим очередную точку, в которой достигается ми-
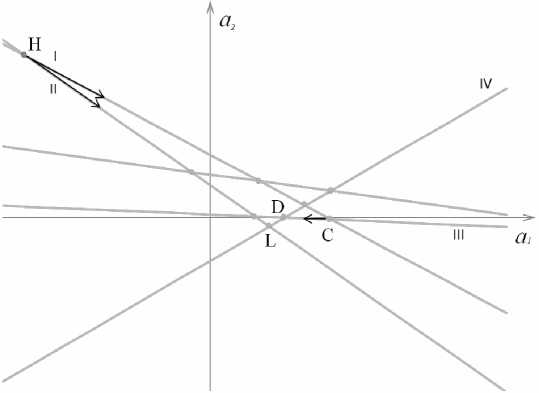
Рис. 2. Спуск по узловым прямым
нимальное значение целевой функции. Далее, сравнивая значения целевой функции в точках C и D , выбираем ту, в которой достигается минимальное значение. Пусть такой точкой является D .
Тырсин А.Н., Азарян А.А.
Допустим, что на прямой IV, проходящей через D , точкой минимума является сама точка D. Тогда в качестве решения выбираем точку D , в которой достигается минимум целевой функции (если бы нашлась другая точка минимума на этой прямой, то из нее продолжили бы дальнейший спуск).
Спуск с использованием разреженных матриц. Двигаясь вдоль прямой l ( kl k m - l) , для нахождения узловых точек, принадлежащих этой прямой, нужно для каждой точки решать систему линейных алгебраических уравнений (СЛАУ) порядка m :
'al + a2xkb2 + a3xkl,3 + ... + amxk^m = Укх’ al + a 2 xk2,2 + a 3 xk 2,3 +... + amxk 2, m = Ук 2,
™ (6>
a + a2xk ,2+ a^Xk ,з+... + amXk , = y Ук ,, 1 2 k m - l ’ 2 3 k m - l ’ 3 m k m - 1 ’ m kkm - l
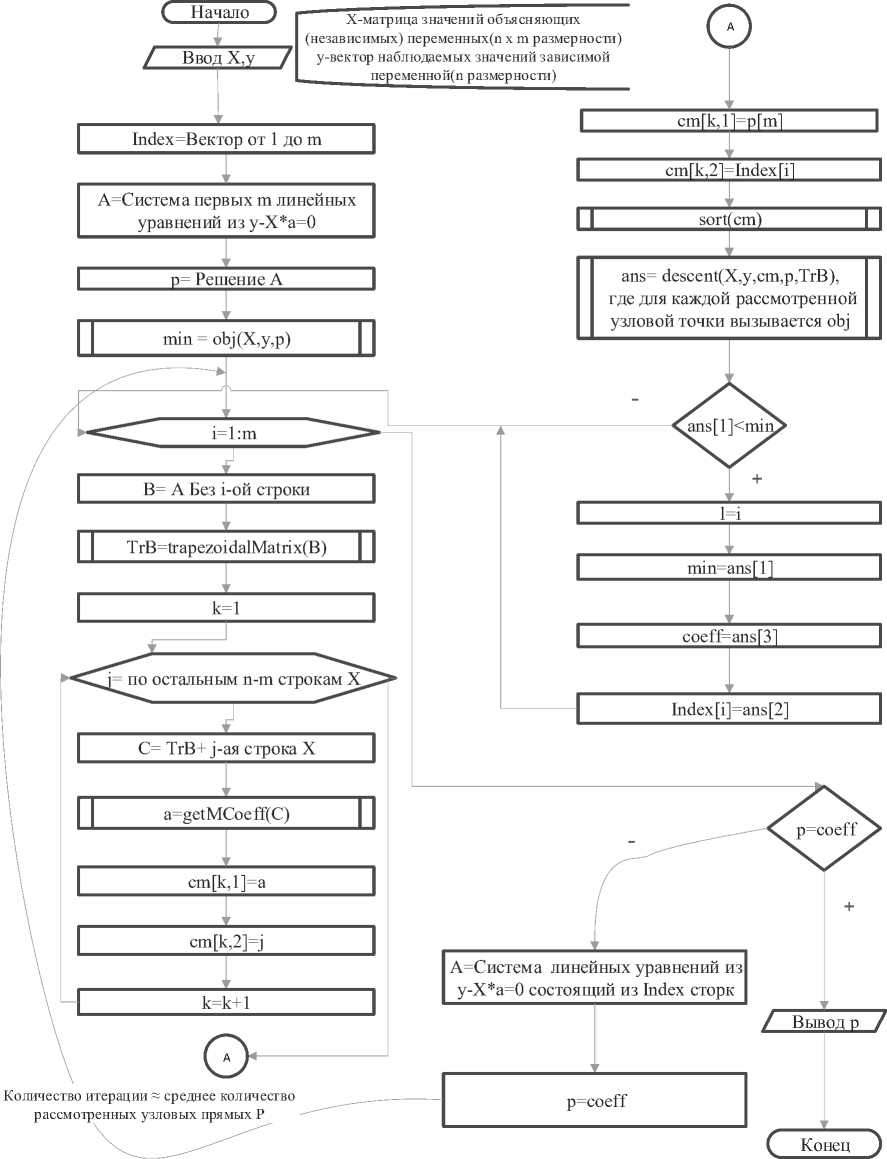
[al + a2xi,2 + a3xi,3 + ...+ amxi,m = Уг ’ где kl < k2 <• Очевидно, что СЛАУ двух различных узловых точек, принадлежащих этой прямой, отличаются лишь одним (последним) уравнением. Следовательно, вычислительная эффективность алгоритма спуска существенно повысится, если для нахождения узловых точек, которые лежат на прямой l(kl, ,km-l), первые (m - l) строк расширенной матрицы, соответствующей СЛАУ (6), предварительно преобразуем с помощью элементарных преобразований к ступенчатому виду. Расширенная матрица СЛУ прямой l(kl, , km-l) имеет вид ( l xkl,2 xkl,3 • xkl, m-l xkl,m ykl ' l xk 2,2 xk 2,3 • xk 2, m-l xk2 ,m Ук2 A( kl,. = ..,km-l ) l xk3,2 xk3,3 • xk 3, m-l xk3 ,m yk3 • • • l V xkm-l,2 x km-l ,3 ■ xkm-l, m-l xkm-l,m ykm-l J Применив алгоритм прямого хода метода Гаусса, преобразуем матрицу A(kl,...,k ) к ступенчатому виду каждой искомой узловой точки имеем расширенную матрицу l xkl,2 xkl,3 • xkl, m-l xkl, m ykl 0 l xk2,3 • xk2, m-l xk2, m ykk2 A(kl,...,km-l,i) = 0 0 l• xk3, m-l xk3, m У'к. ..................... , (7) 00 0 • l x; m y; km-l,m km-l V l x,2 x,3 • xi,m-l xi,m у. J где kl< k2<•< km-l, ie {l,2,^, n}, ig{kl,k2,-, km-l}. Варьируя номер i в (7), найдем все узловые точки, лежащие на прямой l(k1 km-1). Спуск с использованием разреженных матриц и с учетом направления спуска. Вычислительную эффективность алгоритма спуска можно повысить, рассматривая направление спуска. Поясним как. Используя ступенчатую матрицу A(k 1 k 1) и решив СЛАУ, соответствующую расширенной матрице (7), находим значение m-го коэффициента am’k2km-1 ’1) (k1< k2< . < km-1, i e {1,2,., n}, i6 {k1,k2,..., km-1}) для каждой узловой точки. После чего по возрастанию amk1,k2’"'km-1’1) упорядочиваем все узловые точки, которые лежат на прямой l(^ k 1), и выполняем описанный выше алгоритм спуска, но с учетом направления. Если при непосредственном переходе от одной узловой точки к другой значение целевой функции увеличивается, то в этом направлении значение целевой функции будет увеличиваться во всех узловых точках (вытекает из выпуклости целевой функции). Назовем такое направление «плохим». Для осуществления спуска до вычисления значения целевой функции в очередной узловой точке рассматриваем направление спуска. Если оно «плохое», то переходим к следующей точке, не вычисляя в данной узловой точке ни значение целевой функции, ни значения коэффициентов a(k1 ’k2 ’"'km-1 ’1), j = 1,2,., m -1. Анализ вычислительных затрат алгоритмов спуска по узловым прямым Воспользуемся методом статистических испытаний Монте-Карло [14]. В таблице для 1 000 испытаний приведены средние значения общего количества рассмотренных узловых точек L и узловых прямых P (переходов с одной прямой на другую) в алгоритме спуска с использованием разреженных матриц и с учетом направления спуска для некоторых значений n и m. Средние количества рассмотренных узловых точек и узловых прямых в алгоритме спуска с использованием разреженных матриц и с учетом направления спуска n Кол-во узловых точек L Кол-во узловых прямых P m = 3 m = 4 m = 5 m = 6 m = 7 m = 3 m = 4 m = 5 m = 6 m = 7 30 56 91 127 168 211 5,2 6,6 7,7 8,8 9,6 50 85 136 197 262 334 6,1 8,0 9,8 11,3 12,7 100 148 235 348 459 604 7,3 9,9 12,3 14,3 16,8 150 214 337 490 655 847 7,9 10,8 13,7 16,3 19,0 300 397 618 895 1205 1529 9,1 12,7 16,1 19,6 22,9 500 644 1002 1441 1905 2477 9,8 13,9 18,0 21,8 26,0 700 881 1417 2008 2665 3390 10,4 15,0 19,1 23,5 28,1 900 1123 1752 2505 3330 4242 10,9 15,5 20,0 24,4 29,3 1000 1257 1946 2771 3676 4701 11,0 15,7 20,3 25,0 30,1 1200 1461 2341 3345 4400 5626 11,3 16,3 21,0 26,1 31,2 1500 1855 2928 4043 5413 6973 11,8 16,8 21,7 26,9 32,4 1700 2155 3294 4600 6165 7860 12,0 17,1 22,1 27,6 33,1 1850 2278 3520 5004 6763 8602 12,1 17,4 22,5 28,0 33,5 2000 2453 3867 5363 7215 9204 12,2 17,6 22,8 28,2 33,8 Оценим вычислительные затраты спуска с использованием разреженных матриц и с учетом направления спуска. Для этого необходимо оценить средние количества рассмотренных узловых точек L и узловых прямых P. Анализ полученных результатов для различных n и m показал, что L ~ O(mn) , P ~ O(mlnn) . Теорема 3. Алгоритм спуска по узловым прямым имеет вычислительную сложность W = O (m2n2+ m4n In n + m2n ln2n). Тырсин А.Н., Точное оценивание линейных регрессионных моделей Азарян А.А. методом наименьших модулей на основе спуска по узловым прямым Доказательство теоремы 3. Оценим вычислительную сложность всех основных функций, заложенных в базисе алгоритма спуска по узловым прямым. Его схема приведена на рис. 3. Функция trapezoidalMatrix расширенную матрицу размера (m — 1) х (m +1) приводит к трапециевидному виду за (m — 1) итерацию. В ходе i-й итерации выполняется (m + 2 — i)(2m — 1 — 2i) операций умножения и вычитания. Следовательно, общее количество выполненных операций I = mT(m + 2 — i)(2m — 1 — 2i) = 2^ (m + 2 — i)2— 5^ (m + 2 — i) = [ j = m + 2 — i] = 2^ j2— 5m^j . i=1 i=1 i=1 j=3 j=3 m .2 m(m +1)(2m +1) m . m(m +1) Известно, что ^j =— ---—----- и ^j =— ----, поэтому j= 6 £ T 3 ((m +1)(m + 2)(2m + 3) ) < (m +1)(m + 2) ) 1 = 2 • I--5 I — 5 • I--3 I = O (m ). V 6 У V 2 Функция getMCoeff к трапециевидной матрице размера (m — 1) х (m +1) добавляет строку и вычисляет m-й коэффициент. Здесь выполняется (m — 1) итераций. В ходе i-й итерации выполняется 2(m +1 — i) операций умножения и вычитания (кроме первой итерации, во время которой выполняется не 2m, а m операций умножения и вычитания). Следовательно, общее количество m—1 выполненных операций будет равно 2 ^ (m +1 — i) + m — 1 = m2— 1 = O(m2). i=1 Функция obj вычисляет и возвращает значение целевой функции Q(a). Очевидно, что функция obj имеет O(mn) вычислительную сложность. Функция sort реализует сортировку полученного массива. Известно, что сортировка Хоара в среднем имеет для входного массива из n элементов O(nlnn) вычислительную сложность [15]. Функция descent, имея матрицу вида (7) и m-й коэффициент, вычисляет остальные коэффициенты и вызывает функцию obj. Данные действия выполняются циклически, количество итераций примерно равно L /(m • P) = O(mn) /(m•)(m In n)) = O(n /(m In n)). Для вычисления остальных коэффициентов выполняется (m — 1) итераций. В ходе i-й итера- ции выполняется 2i операций умножения и вычитания. Следовательно, общее количество выпол- m—1 ненных операций 2^ i = m2 — m = O(m2). i=1 Поскольку функция obj имеет вычислительную сложность O(mn), то функция descent имеет O(n • (mn + m2) / m In n) вычислительную сложность. Теперь из схемы работы алгоритма получим, что спуск по узловым прямым имеет вычисли- тельную сложность O< m In n • m • I m3 + (n — m) • m2+ (n — m) • ln(n — m) +--n— V m In n = O (m2 n2 + m4 n In n + m2 n ln2 n + m3 n) = O (m2 n2 + m4 n In n + m2 n ln2 n). Отметим, что для n > max(ln2n; m2 lnn ) вычислительная сложность спуска по узловым прямым W = O (m2n2). Выводы Предложены точные алгоритмы реализации метода наименьших модулей при оценивании параметров линейных регрессионных моделей, основанные на спуске по узловым прямым. Данные алгоритмы позволяют значительно снизить вычислительные затраты при точной реализации метода наименьших модулей. Выигрыш достигается за счет того, что вместо перебора узловых точек осуществляется спуск по ним. Вычислительная сложность спуска по узловым прямым позволяет на практике реализовать точное оценивание методом наименьших модулей для любых размеров экспериментальных данных. Рис. 3. Схема спуска по узловым прямым
l xkl,2 xkl,3 xky,m-l xkl,m yl
0 l xk 2,3 • xk2, m-l xk2, m ykT
A( kl,., km -l) =
0 0 l • xk3, m-l xk3, m yk.
• ■ • • ■ • • ■ • • ■ • • ■ • • ■ • • ■ •
.
0 0 0 • l x ‘ m y;
V km-l,m Jmm-l J
Используя ступенчатую матрицу A(kl k l), можно значительно сократить вычислительные
затраты на нахождение всех узловых точек, лежащих на прямой l(^ k l). Действительно, для
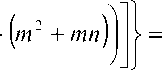
Список литературы Точное оценивание линейных регрессионных моделей методом наименьших модулей на основе спуска по узловым прямым
- Кендэл, М.Д. Статистические выводы и связи/М.Д. Кендэл, А. Стьюарт. -М.: Наука, 1973. -899 с.
- Справочник по теории вероятностей и математической статистике/В.С. Королюк, Н.И. Портенко, А.В. Скороход, А.Ф. Турбин. -М.: Наука, 1985. -640 с.
- Демиденко, Е.З. Линейная и нелинейная регрессия/Е.З. Демиденко. -М.: Финансы и статистика, 1981. -302 с.
- Айвазян, С.А. Прикладная статистика: Исследование зависимостей/С.А. Айвазян, И.С. Енюков, Л.Д. Мешалкин. -М.: Финансы и статистика, 1985. -487 с.
- Bloomfield, P. Least absolute seviations: theory, applications, and algorithms/P. Bloomfield, W.L. Steiger. -Boston-Basel-Stuttgart: Birkhauser, 1983. -349 p.
- Мудров, В.И. Методы обработки измерений: квазиправдоподобные оценки/В.И. Мудров, В.Л. Кушко. -М.: Радио и связь, 1983. -304 с.
- Weiszfeld, E. On the point for which the sum of the distances to n given points is minimum/E. Weiszfeld//Annals of Operations Research. -2009. -Vol. 167, Issue 1. -P. 7-41.
- Акимов, П.А. Уровни неоптимальности алгоритма Вейсфельда в методе наименьших модулей/П.А. Акимов, А.И. Матасов//Автоматика и телемеханика. -2010. -№ 2. -С. 4-16.
- Тырсин, А.Н. Оценивание линейных регрессионных уравнений с помощью метода наименьших модулей/А.Н. Тырсин, К.Е. Максимов//Заводская лаборатория. Диагностика материалов. -2012. -Т. 78, № 7. -С. 65-71.
- Boyd, S. Convex optimization/S. Boyd, L. Vandenberghe. -Cambridge: Cambridge University Press, 2004. -730 p.
- Зуховицкий, С.И. Линейное и выпуклое программирование/С.И. Зуховицкий, Л.И. Авдеева. -М.: Наука, 1967. -460 с.
- Панюков, А.В. Применение массивно-параллельных вычислений для решения задач линейного программирования с абсолютной точностью/А.В. Панюков, В.В. Горбик//Автоматика и телемеханика. -2012. -№ 2. -С. 73-88.
- Рокафеллар, Р. Выпуклый анализ/Р. Рокафеллар. -М.: Мир, 1973. -469 с.
- Михайлов, Г.А. Численное статистическое моделирование. Методы Монте-Карло/Г.А. Михайлов, А.В. Войтишек. -М.: Академия, 2006. -366 с.
- Алгоритмы: построение и анализ/Т.Х. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн. -М.: Вильямс, 2013. -1323 с.


