Точное решение уравнений Рейнольдса для турбулентных течений типа Джеффри - Гамеля в тонком диффузоре

Течение Джеффери - Гамеля от источника, массы (стационарное движение жидкости между двумя плоскими стенками, наклоненными под углом друг к другу) представляет собой один из немногих классических случаев, в котором удается построить точное решение уравнений Навье - Стокса, в вязкой несжимаемой жидкости [1]. В работах [2-6] впервые установлена, возможность построения точного решения для случая ламинарного течения вязкого сжимаемого газа, в клине и конусе. В работе [2] численно решена, задача, о течении газа, в конусе с граничными условиями проскальзывания для температуры и скорости, а в работах [4, 5] рассмотрена аналогичная задача с граничными условиями протекания на. стенках. В работе [6] задача, решена, как в автомодельной, так и в неавтомодельной постановке. Установлено, что автомодельные режимы течения могут быть реализованы в некоторой внутренней области конуса, конечной длины. В работе [7] получено точное аналитическое решение задачи о ламинарном течении газа, от источника, массы в клине, а. в

работе [8] получено аналогичное точное решение для плоской струи вязкого газа от линейного источника импульса. В частном случае, когда температура газа постоянна вдоль линий тока, а коэффициенты переноса - степенные функции температуры, построены аналитические решения. Автомодельные течения вязкого газа в плоском канале при произвольной зависимости коэффициентов переноса от температуры изучены в работе [9].

Заметим, что исследование иных отдельных задач также сводится к решению Джеффери - Гамеля. Так, в [10] показано, что на большом удалении от твердой границы ламинарное течение, индуцированное пространственной пристеночной струей, соответствует течению типа Джеффери - Гамеля около развернутого угла. Задача Джеффери - Гамеля в несжимаемой жидкости при фиксированном расходе изучалась в работе [11], где определены точки бифуркации и области существования течений в плоском диффузоре.

В настоящей работе рассматривается возможность построения автомодельных решений для случая турбулентного течения сжимаемого газа в тонком клине, и в дополнение к результатам работы [12], подробно изучается течение вблизи твердой границы. Показано, что при определенной комбинации определяющих параметров задачи уравнения Рейнольдса могут быть редуцированы к системе обыкновенных нелинейных дифференциальных уравнений. Результаты проведенных численных расчетов полученной системы уравнений сравниваются с аналогичными результатами для ламинарного течения. Установлено, что профиль скорости около стенки практически совпадает с логарифмическим профилем скорости, что косвенно подтверждает правильность проведенного анализа.

2.    Постановка задачи

Рассмотрим стационарное турбулентное течение вязкого сжимаемого газа от источника массы, расположенного в вершине клина с углом раствора 2а (рис. 1).

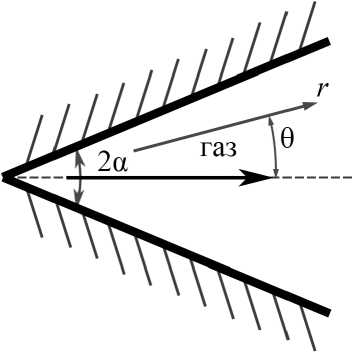
Рис. 1. Схема течения газа в клине

В полярных координатах (г, ») уравнения Рейнольдса имеют вид [13]:

д ,

— (три) = 0,1

дг ди _ дР . 1 Г д С , хх . д ((7'Ө + <^Т'Ө)1

^ридг = - дт ⁺ г ^дг ⁽' ^(<Т" ^{+ аТгг})) ⁺ дю        ^ - ^атӨӨ\ ’

• ^{1    д}р    1 ^д , ₂               .    ^{1 д} (СТӨӨ + СТТӨӨ )

"" '» 1 ,2 д,1'"'1 1      "" г д» ,

„Д - Д + 1» Л„ + „т, 'tL) +1" Л,„ + „) £) -и, д' дг г дг у          дг} г2 д» уд»}

+^ [(.")2 + (^)2 + 2^)²] -       ( '^ )².

Здесь использованы стандартные обозначения для термодинамических переменных: р, р,Т, Һ — соответственно плотность, давление, температура и энтальпия единицы массы; р — коэффициент сдвиговой вязкости, к — коэффициент теплопроводности. Течение в клине предполагается радиальным, так что вектор скорости V = (и(т, Ө), 0). Компоненты тензора напряжений ст определяются следующими выражениями:

ст тт = 2рЕ„ -       (га);    ст өө = 2рЕөө - д^ту- (ти);   ст тө = ст өт = 2рЕтө ,

3т дт                     3т дт

Етт

Эн        и         1 ди дт; Еөө = т; ЕтӨ = 2^

Тензор турбулентных напряжений Стт и вектор турбулентного теплового потока qт со гласно гипотезе Буссинеска [13,14] представляются в следующем виде:

-    2рт д                          2рт д стТтт =2РТЕтт--—   (тн) ; СТТӨӨ = 2РТЕӨӨ--у УТ (ти) ;  СТТтӨ = 2РТЕтӨ,

3т дт                         3т дт qT = -кт ЧТ.

В настоящей работе рассматриваются течения в узких клиньях, т.е. при а ^ 1. В этом случае компонентами тензора вязких напряжений ст_тт и стөө можно пренебречь по сравнению с компонентой ст_тө, поскольку ди/дт и и/т по порядку величины оказываются значительно меньше производной ди/дӨ. По этой же причине компоненты стт_тт и сттөө тензора турбулентных напряжений малы по сравнению с стт_тө- Тогда исходная система уравнений (1) — (4) упрощается и ожидаемо принимает вид уравнений пограничного слоя:

дт ^(тР^и) = ⁰

Эи Эр 1 д Г        Эи ридт = - дт + т2 дӨ [(р + рт) дӨ

= _ 1 Эр тдӨ, ри^ = ^ + 4(к + кт) 2) + (р + рт) (1УГ .          (8)

дт дт т2 дӨ \         дӨ)           \т дӨ /

В соответствии с теорией пути смешения Прандтля коэффициент турбулентной вязкости рт определяется по формуле [14]:

Р^² рт = — т

ди дӨ

где I — длина пути смешения. Турбулентный коэффициент теплопроводности кт связан с рт известным соотношением:

Величина турбулентного числа Прандтля Ргт оказывается близкой к единице практически во всем поле течения, поэтому для простоты расчетов примем далее Ргт = 1 [15].

В качестве характерных масштабов газодинамических параметров выберем значения ро, ио, То в некоторой произвольной точке на оси клина т = то, Ө = 0 и перейдем к безразмерным переменным: р, р, Т, и, т. Уравнения (5) — (8) в этих переменных содержат следующие параметры подобия: число Прандтля Рг = рс-р/к, число Рейнольдса Reo = роиото/ро, число Маха Мо = ио/ТрКТо и отношение теплоемкостей у = Ср/с^. Здесь ро — значение коэффициента вязкости при Т = То.

3.    Вывод определяющих уравнений

Автомодельное решение для плоского радиального турбулентного течения газа по аналогии с «ламинарным» случаем [7] ищем в виде

^1-U гт

р - г^т-1р(Ө);

- _ Р(о) _

^Р    үт+1 ^;

_{Т -} ТМ- ү2т ^;

р= (ТМ

'I       ^2т     '

К ^- ЕТI Pr

(Ю)

Показатель степени г в (10) для плотности подбирается таким образом, чтобы уравнение неразрывности (5) выполнялось автоматически, а для давления степень г определяется из уравнений импульсов (6) и (7):

__Эи Эр 1

(И)

^рпэТ ~ дг ~ гт+2 -

Показатель степени г для температуры находится из уравнения состояния, записанного с учетом выбора масштабов:

уМ2р(0)- р(9)Т(9).

В формуле для пути смешения Прандтля (9) присутствует неизвестный параметр I. В плоском радиальном течении выражение для I имеет вид [13,14]:

I - уг(а - |9|), где у — некоторый коэффициент, числовое значение которого определяется с использованием экспериментальных данных. Формулу (9) в этом случае можно переписать в следующей форме [12]:

It ^- Р⁽⁹⁾У2⁽« ^{- |9|)}2

Ни(Ө) НӨ

Окончательно выражения для компонент тензора турбулентных напряжений при а ^ 1 принимают вид

^ат-гт — ^атөө — °;

а™ -  ■  - -|»|)2 ^ ^

Но Но

Гт+2 .

Тогда слагаемые в уравнениях (6) — (8), отвечающие за турбулентные напряжения, будут иметь порядок

ат 1

г    гт+2 ’

а порядок вязких членов в уравнениях (6) — (8) соответственно

а 11

г   г2т^ гт+2 ^-

Легко заметить, что выражения (11), (13) и (14) имеют одинаковую степень г при вы

полнении условия

2тк - 0.

После подстановки (10) и (12) в уравнения (6) — (8) получаем следующую нелинейную систему обыкновенных дифференциальных уравнений:

^(т + 1)р + три² + ¹ -^ (т^кНпА + у² 1- Reo Но у Но / Но

(Р(а -|9|)2 НЛ НО -°,       (¹⁵)

у            Но Но у

* = 0

de ,

7 + 1 ) _        1         d

7 — 1      M2PrReo(7 — 1) de

с з)<(:)" -

у2      d

-

+ M2 PrT (7 — 1) de

f P^(a - ^|е|)2ДУ) ^{+ у}2Р^(а - ^|e|)2 de

с симметричными граничными условиями:

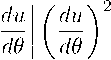
„(0) _ 1,

T(o)_i,  Р(о)_ М2,

и(±а) _ 0,

T(±а) _ Tw.

Таким образом, установлено, что для турбулентных течений вязкого газа в тонких клиньях исходные уравнения в частных производных (5) — (8) можно свести к системе обыкновенных дифференциальных уравнений (15) — (17) , другими словами, в соответствии с установившейся терминологией [14], получить точное решение.

При проведении практических расчетов необходимо знать числовое значение параметра у. В работе [15] с использованием экспериментальных данных для турбулентных течений сжимаемого газа найдено, что значение у приближенно можно считать равным у _ 0.4. С учетом этого окончательно получаем замкнутую краевую задачу (15) — (18), которая описывает автомодельные турбулентные течения вязкого газа в тонком клине.

4.    Численное исследование автомодельного решения

Ниже приведены результаты численных расчетов краевой задачи (15) — (18) при к _ 0, т _ 0. Для определенности вновь примем 7 _ 1.4, Pr _ 0.71. В этом случае температура и скорость остаются постоянными на оси клина, а коэффициент вязкости ^о постоянный во всем поле течения. В проведенных расчетах используется численный метод [16], с успехом примененный ранее при расчете ламинарного течения газа [17]. Решение зависит от четырех параметров задачи: чисел Мо и Reo на оси клина, температуры стенки T_w и полуугла раствора клина а. Для каждого а задавался некоторый на бор численных значений Мо, а значения Reo и T_w подбирались таким образом, чтобы выполнялись граничные условия (18).

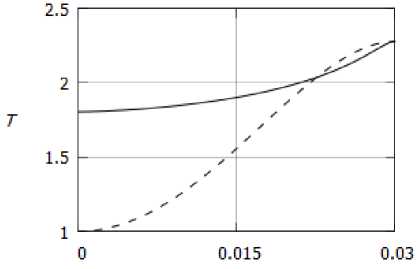
Сравнение зависимостей Reo _ Reo(Mo) и T_w _ T_w(Мо) для ламинарного и турбулентного случаев представлено на рис. 2а, 26 для течения в клине с а _ 0.03 рад.

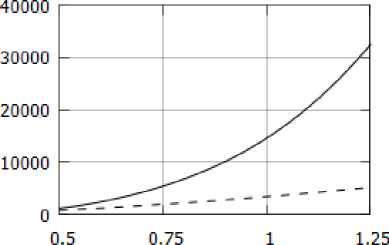
м0                                             м0

а)                                                         б)

Рис. 2. Зависимость a) Reo б) и Tw от числа Маха на оси клипа в турбулентном (сплошная линия)

и ламинарном (пунктирная линия) течении

Видно, что при одинаковых значениях Mo температур а на стенке T_w и число Reo в турбулентном течении выше, чем в ламинарном. Последнее можно объяснить тем, что в турбулентном течении дополнительно к вязкой диссипации происходит диссипация энергии турбулентных пульсаций, которая тоже переходит в тепловую энергию, вследствие чего температура на стенках повышается.

Сравним ламинарные и турбулентные профили скорости и температуры при одинаковом расходе. Пусть температура стенок в обоих течениях одинакова. Расход газа запишем в следующем виде:

c pct

Q = Topo^o / р(Ө)и(Ө) dd = %Reo / р(Ө)и(Ө) dd = poReoQo. J —c J — c

Здесь po — значение коэффициента вязкости на оси канала. Требуется найти такую комбинацию параметров Reo, Qo в ламинарном и турбулентном течениях, чтобы расход Q в размерных переменных был одинаковым для обоих режимов течения. Такой комбинации параметров соответствует, например, Reo,L = 28019, Q o ,l = 1.52 • 10-2 при M o ,l = 3 и Reo,T = 19000, Qo,_T = 2.31 • 10-2 пр и Mo,_T = 1.2.

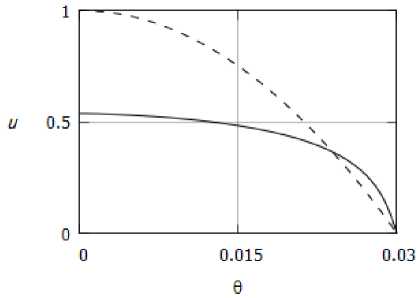
Сравнение профилей скорости и температуры при одинаковом расходе, отнесенных к значению скорости и температуры на оси клина в ламинарном течении, представлено на рис. За, 36 для клина с полууглом раствора a = 0.03 рад. Заметим, что уровень скоростей в ламинарном течении при этом оказывается выше, чем в турбулентном. Одинаковый расход обеспечивается большим значением плотности в турбулентном течении.

а)

Рис. 3. Профиль а) скорости, б) температуры; пунктирная линия — ламинарное течение, сплошная линия — турбулентное течение

б)

Средняя температура в турбулентном течении на оси клина также оказывается больше, чем в ламинарном течении, поскольку, как было указано выше, в турбулентном течении часть кинетической энергии переходит в турбулентные пульсации, что и приводит к повышению температуры внутри клина.

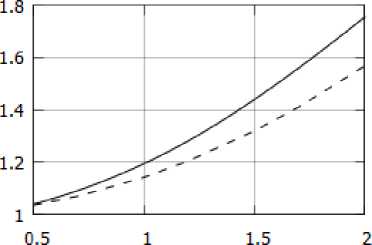
Рассмотрим теперь автомодельное турбулентное течение в более общем случае (ттг = 0, к = 0), а именно при степенной зависимости коэффициентов вязкости и теплопроводности от температуры p(T ) = T ^o'76. По-прежнему будем считать у = 1.4. Pr = 0.71. Проведем сравнение полученного в этом случае профиля скорости с классическим логарифмическим профилем скорости, который для плоского радиального случая имеет вид

„ ~ — ln ( " т (“ ^- »> ) ₊ С. _|19| А А

Здесь и_т = ^ t _w /р, где t _w — напряжение трения на стенке, С — некоторая константа.

Пусть имеет место турбулентное течение вязкого газа в узком клине с полууглом раствора a = 0.02 рад при Mo = 1.5 и Reo = 2.1 • 105. Полученный в расчетах автомодельный профиль скорости в логарифмическом масштабе показан на рис. 4.

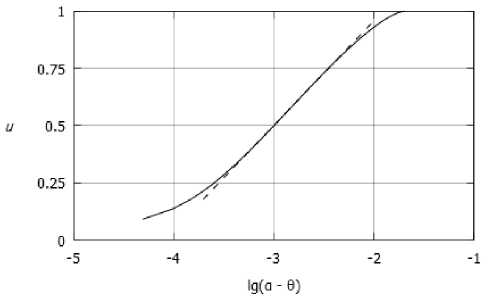
Рис. 4. Профиль скорости турбулентного течения газа, в топком клипе. Сплошная линия — автомодельный профиль скорости, штриховая линия — логарифмический профиль

Как видно из рис. 4, в области между осью и стенкой клина, наблюдается участок, на. котором профиль скорости оказывается очень близким к логарифмическому профилю, построенному по формуле (19). Аналогичное сравнение, но уже в физических координатах представлено на. рис. 5.

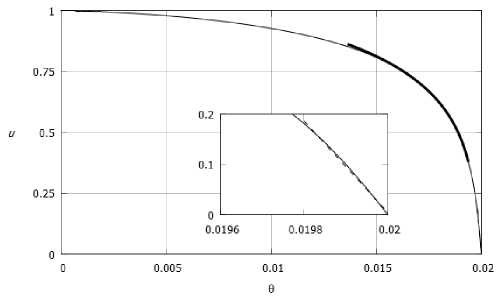
Рис. 5. Профиль скорости в физических координатах: сплошная линия — автомодельный профиль, жирная линия — логарифмический профиль скорости, штриховая линия — линейный профиль

Вблизи стенки автомодельный профиль практически совпадает с логарифмическим профилем, рис. 5. На очень малом расстоянии от стенки, как и положено, наблюдается участок линейного профиля скорости (ламинарный подслой).

5.    Заключение

Установлена возможность построения точных автомодельных решений для стационарного турбулентного течения газа, от источника, массы в тонком клине. Показано, что в этом случае исходные уравнения в частных производных сводятся к системе обыкновенных дифференциальных уравнений.

Полученные в ходе численных расчетов турбулентные профили скорости и температуры сравниваются с соответствующими ламинарными профилями при условии одинакового расхода, газа, и одинаковой температуры стенок. Показано, что рассчитанный профиль скорости вблизи стенки согласуется с известным логарифмическим профилем.