Точное решение задачи взаимодействия неоднородных волн с плоской границей

4k2qs-(k2 +s2)2

sin 0

-exp(qz)dk.

1 f

PM pQM k-kXx k-k2x>

. R(kXx) S(k2x) R(kr) + lx/ - p --^

VAx k-k2x)

P(kr)

4k2qs-(k2 +s2)2

COS0 +

4k2qs-(k2 +s2)2

sin0>exp(sz)dk.

Представление (3) дает точную волновую картину во всем пространстве, описывающее как поле объемных волн, так и поверхностных.

На плоскости комплексного переменного к подынтегральные функции в (3) имеют ряд особых точек: полюсы, соответствующие распространению поверхностных волн, точки ветвления k_t, ki. Методы выбора пути интегрирования и приемы вычисления аналогичных интегралов хорошо известны в акустике [3].

Применение метода перевала к интегральному представлению решения (3) приводит к выра

жениям для диаграммы направленности расходящихся объемных волн:

У _ /2л- cos²/

_? 2к^_х-к² 2к_Хху1к^-к^_х к^ту-^ k^iny-k^

+ Р

^-к_2х^к² -к_2х [ 2к_Хх -к² k[Siny-k_2x k_tsm.y-k_Xx

к2^ ехр(/кгр-1^-),

- /^ cos² у ‘~W k³D_t

p ^2x~^f ^Ix^l ^br k_t sin у -k_2x ^sm/-^.

+ р

^2x^1  ^2x ^2x j . ^-k²_x—k²

^-^ ^iktp-i^),

kt sin у -k2x     ktsmy-k}x где Dj = 4 sin2 о cos2 ®\lsm.2 со-£2 - (2 sin2 <у -1)2, Dt = 4 sin2 у cos2 y^sin2 y-£2 - (2 sin2 у - e2 )2,

E = kjk] . Здесь у - азимутальный угол, отсчитываемый от оси z.

Амплитуда смещений возрастает как для продольных волн (кривая 1), так и для сдвиговых (кривая 2) по мере уменьшения угла излома, достигая максимума при угловой координаты плоскости близких к 60° (рис. 2), а затем уменьшается до нуля. Объемные волны для приведенного дюралюминиевого материала возникают при угловой координате 0_О⁼ 15°.

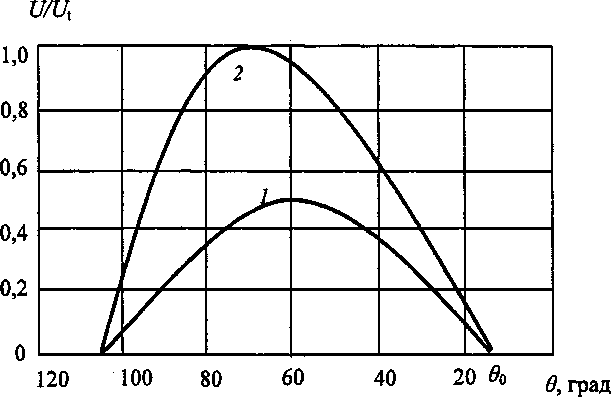
Рис. 2. Распределение амплитуд смещений в объемных волнах в зависимости от угла клина. 1 - продольные волны, 2 - сдвиговые волны

Максимумы смещений в объемных волнах у продольных (рис. За) и поперечных (рис. 36) лежат в направлении азимутального угла 30°. При уменьшении угла излома происходит как изменение амплитуды смещений, так и небольшое смещение максимума диаграммы направленности.

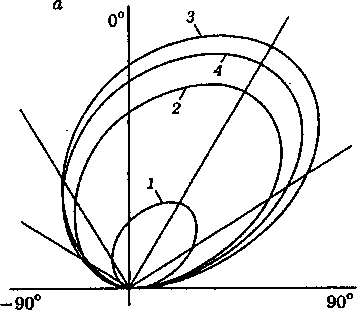
Рис. 3. Диаграмма направленности продольных (а) и сдвиговых (б) волн при различных углах клина.

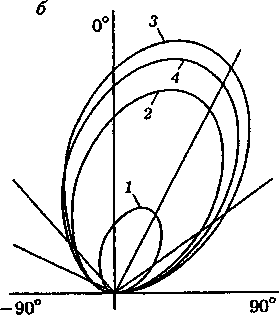
1 - 150°, 2 - 140°, 3 - 120°, 4-100°

Рассмотрим важный с точки зрения понимания физических процессов - отражение от плос

кости, составляющей прямой угол с поверхностью (рис. 4).

Поверхностная волна падает на плоскость по нормали, а максимальное смещение в отраженной объемной волне приходится на угол, примерно равный 0_й (см. рис. 4). Это соответствует простым физическим представлениям о том, что направление упругой энергии не совпадает с направлением волнового фронта. Угол сноса между групповой и фазовой скоростью определяется соотношением: 0о ⁼ arccos cjc_r.

Гармоники с к = к_п создадут поле поверхностных, прошедших на наклонную поверхность волн, которые описываются вкладом вычетов, определяемыми полю-

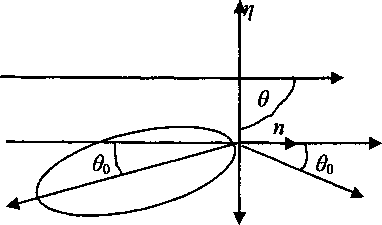
Рис. 4. Распределение амплитуд смещений в объемных волнах при падении на прямоугольный клин

сами в подынтегральном выражении:

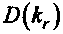
COS0 +

РМ

Л Az

1 iy = — ^Y In

D^

sin 5

•exp(sz)

PM pQM k-kXx k-k2x,

R^

RM nsM]P(k) "k-k p~k-k~ (

D^

COS 6 +

TZT pTZk~ k-k

D^           ’

■exp(sz),

где D(k_r) =-%k_rqs + 4k, —+—

-8kr^-k^.

Гармоники c kr > к > kt описывают волны, скорости которых стремятся к скорости поверхностной волны по двум причинам. Во-первых, в твердых телах на границе сред происходит взаимная трансформация продольных волн в сдвиговые. Поэтому при распространении поверхностной волны, состоящей из сдвиговых и продольных составляющих, скорость волны будет постепенно падать, так как сдвиговая волна движется медленнее продольной. Во-вторых, с уменьшением скорости волны толщина пограничного волнового слоя растет. При этом происходит перестройка его пространственной структуры. Это ведет к тому, что плотность энергии волны снижается, рассредоточиваясь по большему объему. Скорость волны монотонно будет уменьшаться до тех пор, пока скорости продольной и сдвиговой составляющих не выровняются соответственно скорости поверхностной волны. Этот эффект является специфическим в твердых телах и не имеет анало гов в других средах.

Независимость волнового вектора от углового параметра плоскости свидетельствует о вырождении задачи.

Картина волн, возбуждаемых падающей неоднородной волной в алюминии, согласуется с приводимыми расчетами (опытные данные из работы [2], получены для дюралюминиевого кли на) (рис. 5).

. Как показывает анализ, амплитуда (см. рис. 5) прошедшей волны на плоскость для вырожденного случая (9 < 9_й) остается неизменной, а для другого - носит сложный характер, являясь результатом совместного действия и конкуренции нормальных и сдвиговых составляющих волновых возмущений, вызываемых падающей волной.

При малых углах 9 основной вклад в формирование пространственной структуры рассеянного акустического поля вносят касательные составляющие возмущающих сил (кривая

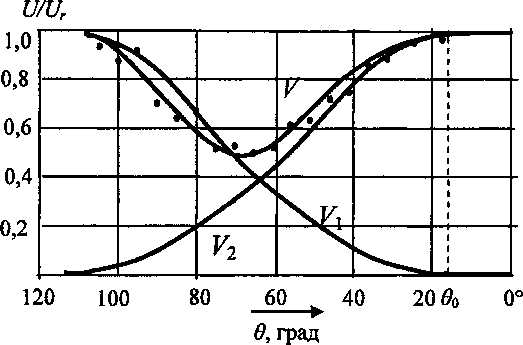
Рис. 5. Зависимости коэффициентов прохождения волны на плоскость от угла 6

Pi). С увеличением угла 9 вклад этих сил падает, но в то же время увеличивается влияние нормальной составляющей (кривая К2), монотонно достигающей максимума. Характер эволюции простран ственной структуры поля существенно зависит от углового положения плоскости.

В данном сообщении получено решение задачи дифракции поверхностных волн на наклонной плоскости. Выявлены физические аспекты возникновения поля поверхностных и объемных волн, вызываемых падением на плоскость неоднородной волны. Трансформация первичной волны в объемные является основным механизмом, определяющим потери энергии колебаний при переходе поверхностной волны на наклонную плоскость.

Определено, что азимутальное направление максимума поля рассеянных объемных волн определяется волновым вектором фазовой скорости поверхностной волны, который не совпадает по фазе с волновым вектором групповой.