Точность численного решения уравнения диффузии-конвекции на основе разностных схем второго и четвертого порядков погрешности аппроксимации
Автор: Сухинов Александр Иванович, Чистяков Александр Евгеньевич, Якобовский Михаил Владимирович
Рубрика: Вычислительная математика
Статья в выпуске: 1 т.5, 2016 года.
Бесплатный доступ
В работе рассмотрены схемы второго и четвертого порядков погрешности аппроксимации для решения задачи диффузии-конвекции. Для модельной начально-краевой задачи, в случае когда функции правой части и начального условия представимы конечными суммами рядов Фурье по тригонометрическому базису, исследована точность разностных схем. Установлено, что точность численного решения зависит от количества узлов приходящихся на половину длины волны, соответствующей наиболее высокочастотной гармонике в конечной сумме ряда Фурье, необходимой для описания поведения расчетных объектов. Получены зависимости погрешности аппроксимации диффузионных слагаемых разностными схемами второго и четвертого порядков точности от количества узлов. Выполнено сопоставление результатов расчета двумерной задачи диффузии-конвекции и задачи Пуассона на основе схем второго и четвертого порядков точности. В работе обоснована целесообразность перехода к схемам повышенного порядка точности при решении прикладных задач и из полученных оценок нетрудно получить численные значения выигрышей во времени счета при использовании схем повышенного порядка точности.
Точность, разностные схемы, уравнение диффузии-конвекции, погрешность аппроксимации
Короткий адрес: https://sciup.org/147160584
IDR: 147160584 | УДК: 519.6 | DOI: 10.14529/cmse160105
Текст научной статьи Точность численного решения уравнения диффузии-конвекции на основе разностных схем второго и четвертого порядков погрешности аппроксимации
Работа, посвящена, изучению дискретных аналогов операторов конвективного и диффузионного переноса второго и четвертого порядков точности. Основной целью данной работы является исследование точности разностных схем, аппроксимирующих операторы конвективного и диффузионного переноса, в зависимости от количества, узлов, необходимых для описания объекта изучения. В соответствии с поставленной целью решены следующие задачи: выполнена, оценка, решения при переходе к сеточным функциям; для схем второго и четвертого порядков погрешности аппроксимации выполнены оценки погрешности в зависимости от количества, узлов; выполнено сопоставление результатов расчета, двумерной задачи диффузии-конвекции и задачи Пуассона на основе схем второго и четвертого порядков точности. В работе обоснована, целесообразность перехода, к схемам повышенного порядка. точности при решении прикладных задач. Из полученных оценок нетрудно получить численные значения выигрышей во времени счета, при использовании схем повышенного порядка, точности.
Настоящая работа, является логическим продолжением работы [1], в которой описана, построенная библиотека, итерационных методов, предназначенных для решения сеточных уравнений с самосопряженными и несамосопряженными операторами при помощи схем по- вышенного порядка точности, учитывающими заполненности ячеек на многопроцессорной вычислительной системе. Предложенные схемы были разработаны для решения задачи восстановления рельефа дна акватории на основе гидрографической информации [2], а также применены при разработке программного комплекса, предназначенного для расчета трехмерных полей скоростей течений в мелководных водоемах [3].
1. Аналитическое решение уравнения диффузии
Рассмотрим первую начально-краевуто задачу для неоднородного уравнения теплопроводности вида ut = ku'Xx + f, 0 < x < l, 0 < t < T,(1)
u(x, 0) = ug(x), u(0, t) = 0, u(l, t) = 0.(2)
В отношении функций u(x,t) и f (x, t) будем предполагать их представимость в виде рядов Фурье по тригонометрическому базису:
-
u(x, t)= ^ cm (t) sin(wmx),f (x, t) = ^ Cm) (t) sin(wmx),(3)
m=1m=1
где ш = ^/l. Cm ) = 2 Jl f (x) sin(wmx)dx. C^u) = 2 Jl f (x) sin(wmx)dx.
Наряду с задачей (1) - (3), которую будем называть «точной» непрерывной задачей, рассмотрим первую начально-краевую задачу с «усеченной» правой частью
N -1
f(N)(x, t) = 2 Cf) (t)sin(wmx),(4)
m=1 и «усеченными» начальными условиями
N -1
u(N)(x,t) = ^2 Cmu) (0)sin(wmx),(5)
m=1 для задачи вида
(u(N))t = k(u(N))"x + f(N), 0 < x < l, 0 < t < T,(6)
u(N)(x, 0) = u(N)(x), u(N)(0, t) = u(N)(l, t) = 0.(7)
Следует отметить, что такая постановка возникает, например, в случае табличного способа задания функции f и uq ряды будут ограничены N — 1 гармониками т.к. для восстановления непрерывной функции применяется интерполяционный тригонометрический полином [4], где N — количество дискретных значений функции. Оценим «близость» функций u(x,t) и u(N)(x,t) — соответственно решения «точной» и «усеченной» задачи, введя функции
w(N)(x, t) = u(x, t) — u(N)(x, t), g(N)(x, t) = f(x, t) — f(N)(x, t), v0N)(x) = u0 (x) — u(N)(x) (8) имеем вспомогательную задачу
(w(N))t = k(w(N))Xx + g(N), 0 < x < l, 0 < t < T, (9)
w ( N ) (x, 0) = v,N) (x), w ( N ) (0, t) = w ( N ) (l, t) = 0.
Для решения задачи (9) - (10) справедлива оценка в гильбертовом пространстве С^ для любого t > 0 [5]:
t
IPNWL < ^ (x)L + ^ ||g
HD
Известно, что для класса функций периода 2л, имеющих производную порядка а, удовлетворяющий неравенству ^(“ (x)| < —, имеет место оценка остаточного члена ряда (3) для любого натурального а [6]:
sup
0 N-1 ^(x) — ^C(^ sin(mx) m=1 4K In N л2N“ + o(N0. Учитывая оценку (12), а также соотношения (9) - (10), из неравенства (11) получим оценку для любого t > 0 и И Ki/N2 + TK lnN 1 \ РДМ.^^ < 4 --2N-2+ O (N“-2 ) -1 = x |U0“)(х/ш)| ,-2 = nmax |f(“ 2)(x/^,t) 0 Оценка (13) гарантирует сходимость решения «усеченной» задачи к решению точной задачи при N ^ то при достаточно гладких входных данных в смысле выполнения неравенства (12), при а > 3. В дальнейшем u(x,t) предполагается принадлежащей классу C(4) [0 < x < l] в случае разностной схемьi с погрешностью решения O(h? + т^) (см п. 3) л классу C(6) [0 < x < l] в случае схемы с погрешностью O(h4 + т^) (см п. 4). где 3 зависит от веса схемы. Для остальных функций входящих в постановку исходной задачи (1) — (3) также предполагается необходимая гладкость. Функции u(N) и f(N) при подстановке в (1) приводят к соотношению: /N-1 \ ' /N-1 \ "N I ^ Cu sin(wmx) I = k I ^ Cu sin(wmx) I + ^ Cf) sin(wmx). Меняя очередность операции дифференцирования и суммирования ряда получим: N-1 , N-1 sin(wmx)) + У2Cnf) sin(wmx). n=1 12 (CmU)(t)) t sin(wmx) = ^ kCu (-ш2m2 Принимая во внимание линейную независимость функций sin(wmx), получим: (cmu)(t))t=-k^2m2cmu)+cmf).(i^ Решение уравнения (14) примет вид: (f)^(f) Р(u) (u) _ Cm -kw2m2t , Cm Cm(t) Cm,0 кш2т2e +кш2т2. После проделанных преобразований и вычислений, с учетом заданных начальных и граничных условий, будет найдена искомая функция: N—1 / / , х C(f) \ C(f) \ u = 5=1 ((Cm,0 — w)eкшmt + wJsin(^mx). (io)
2. Точность численного решение уравнения диффузиина основе разностных схем второго порядка погрешности аппроксимации Аппроксимация уравнения (1) примет вид [7]: n+1 ,,n n+a _ n + a ^ n+a ui — ui = kui+1 i + ui — 1 + f. T h2 i, где сП+а = стсП+1 + (1 — ст) cn ст G [0,1] — вес схемы [8]. Будем использовать представления (4), (5) функций и и f при решении задачи (16) ^N=1 (Cm (tn+1) — Cm (tn)} Sin(wmXi) \tau N-1 = к £ Cm (t"+a) m=1 N-1 + ^2 Cm) sin(wmx). m=1 (sin(wmxi+1) — 2sin(wmxi) + sin(wmxi-1)) h2 Преобразуем полученное выражение и, принимая во внимание линейную независимость функций sin(wnx). получим: C^ (tn+1) — C^ (tn) \tau = k 2H^mh)---1) C(u) (tn+a) + Cf). (1 _) Лемма 1. При выполнении оценок (12) аппроксимации задачи (1) - (2) разностными схемами (16) для каждой гармоники функции решения и скорость диффузионного обмена к меньше реальных значений и отличаются на. величину ai = 1 — 2 (1 — cos (wmh)) / (wmh)2. Доказательство. Из (6) при т ^ 0 следует: (C(u)(t))t = -к О^^Дт^ДЛ) ^2m2Cs (tn+a)+Cf). В силу (14) решение, полученное на основе схемы (5) соответствует решению уравнения ut = k*u'Xx + f, к* = к (1 — a1), a1 = 1 — 2 (1 — cos (^mh)) / (^mh)2. Лемма доказана. Рассмотрим величину ai = 1 — 2(1 — cos (^mh)) / (^mh)2: 2(1 — cos(wmh)) a 1 w2m2h2 =1- 2(1 — <^^ + I^Mh)4 + O (h«) — 1) („mh)2 —^2m2 h2 12 + O (h4). Замечание 1. Имеет место оценка wmh < л. Также следует отметить, что величина r = л/ (ymh) описывает количество узлов, приходящихся на половину периода волны (на описание объекта). Из полученной оценки видно, что точность численного решения зависит от количества узлов приходящихся на половину периода волны. На рис. 1 приведен график функции «1 (r) = 1 — 2 (1 — cos (л/r)) / (л/r)2, описывающей зависимость погрешности аппроксимации диффузионных слагаемых разностными схемами от количества узлов, используемых для описания объекта. Рис. 1. График зависимости погрешности аппроксимации диффузионных слагаемых разностными схемами от количества узлов, используемых для описания объекта Аналитическое выражение соответствующее численному решению запишется: N-1 u = ^ (с^ e-k(1-»i(N/m^m22t sin(wmx). m=1 Замечание 2. При описании диффузионных слагаемых разностными схемами погрешность аппроксимации в наихудшем случае задании функции источников (в виде точечных источников г=2) будет составлять 18,9%.
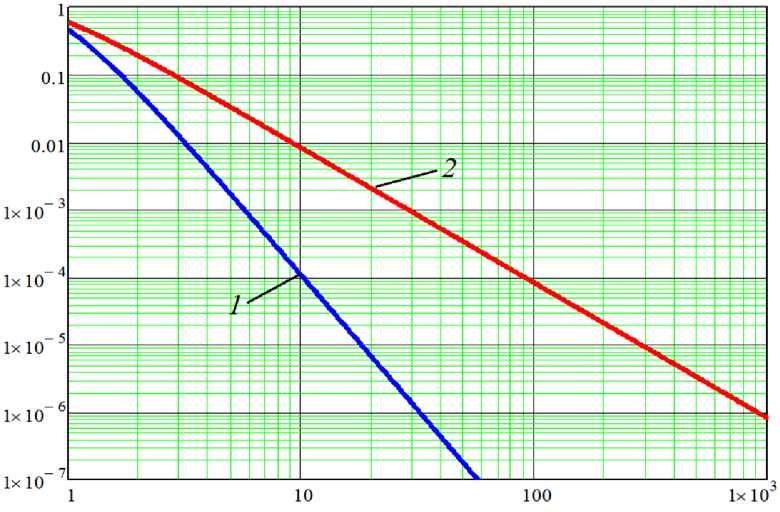
3. Точность численного решение уравнения диффузиина основе разностных схем четвертого порядкапогрешности аппроксимации Рассмотрим случай разностной аппроксимации схемами повышенного (четвертого) порядка точности [9]: и^ — uin \tau п+а п+а п+а п+а „.п+а k —ui+2 + 16ui+1 - 30ui + 16ui-1 — ui-2 +fi. Будем использовать представления (2) функций и и f при решении задачи (18): Ет=1 (du (tn+1) - Cm (tn)) sin(wmxi) \tau ^^C(u) (^+СТ ) = k ) m , 9----(— sin(wmxi+2) + 16sin(^mxi+1) — 30sin(^mxi) + h2 m=1 \infty +16sin^mxi-^ — sin(wmxi-2)) + ^^ Cm) sin(wmx). m=1 Преобразуя полученное выражение и принимая во внимание линейную независимость фупкщш sin(wnx). получим: Cm (tn+1) — Cm (tn) —2 cos(2wmh) + 32 cos(wmh) — 30 C^ 0+4 + Cf). (19) T = k 12h2 Лемма 2. В условиях выполнении оценок (12) при решении задачи (1) разностными схемами (18) для каждой гармоники функции решения и скорость диффузионного обмена к меньше реальных зпачсшш и отличаются на. величину «2 = 1 — (15 — 16 cos (wmh) + cos (2wmh)) /6 (umh)2. Доказательство. Аналогично лемме 1. Рассмотрим величину «2 = 1 — (15 — 16 cos (wmh) + cos (2wmh)) /6 (wmh)2: «2 = 1 — (15 — 16 cos (wmh) + cos (2wmh)) /6 (штК)"2 = (wmh)4/90 + O(h6). Функция, описывающая зависимость погрешности аппроксимации диффузионных операторов разностными схемами четвертого порядка точности от количества узлов на структуру примет вид «2 (r) = 1 — (15 — 16 cos (я/r) + cos (2я/г)) /6 (я/r)2. На рис. 2 приведены графики функций, описывающие зависимости погрешности аппроксимации диффузионных слагаемых разностными схемами второго и четвертого порядков точности от количества узлов. Замечание 3. При описании диффузионных слагаемых разностными схемами погрешность аппроксимации может составлять для данных слагаемых в наихудшем случае задании функции источников 5,4 %.
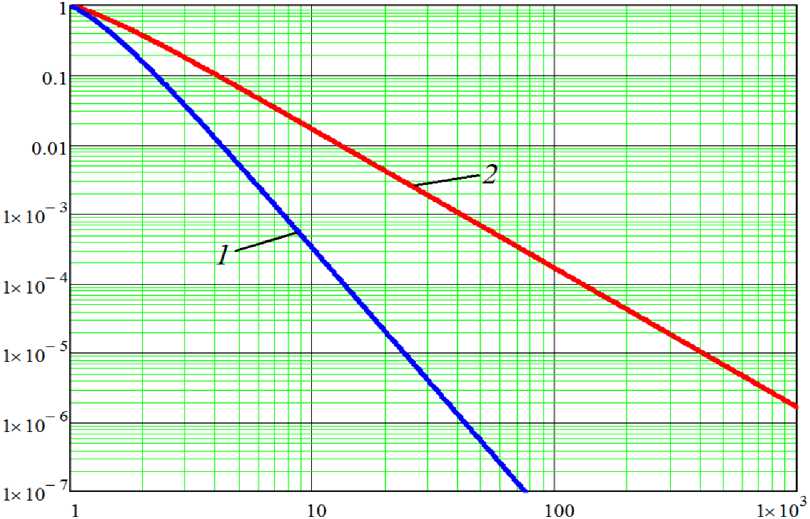
4. Погрешность аппроксимации операторов конвективного переноса Рассмотрим краевую задачу диффузии-конвекции с начальными и граничными условиями [10, 11], т.е. найдем аналитическое решение уравнения ut + vuX = kuXx, 0 < x < l, 10, (20) удовлетворяющее начальному условию u(x, 0) = uq(x)h граничным условиям u(0,t) = 0, u(l, t) = 0. t > 0. Для решения задачи (20) выполнить переход в подвижную систему координат у = x — vt при этом решение задачи сводится к решению уравнения диффузии: ut = ku^y аналитическое решение которого описано выше. Рис. 2. График зависимости погрешности аппроксимации операторов диффузионного переноса разностными схемами от количества узлов, используемых для описания объекта: 1 — схемы четвертого порядка точности, 2 — второго Рассмотрим разностную производную оператора конвективного переноса u'x второго порядка точности. Используем представления (12) функции u: Ui+1 - Ui-1 2h N-1 = e cmu) (t) m=1 (sin(шmxi+1) — sin(шmxi-1)) 2h = £ СУ (t) sin("mh) co<™). m=1 Непрерывная производная с учетом представления (12) примет вид: N-1 uX = Е Cu (t) шт сов(штх). m=1 Таким образом, функция, описывающая зависимость погрешности аппроксимации конвективных операторов разностными схемами от количества узлов на структуру примет вид: «3 (r) = 1 — sin (^/r) / (^/r)- Для схемы четвертого порядка точности u\primex —ui+2 + 8ui+1 — 8ui-1 + ui-2 \simeq 12h оператора конвективного переноса не трудно получить функцию, описывающую зависимость погрешность аппроксимации данного оператора от количества узлов, приходящихся на половину периода волны «4 (r) = 1 — (8sin (^/r) — sin (2^/r)) / (6^/r). На рис. 3 приведены графики функций, описывающие зависимости погрешности аппроксимации конвективных слагаемых разностными схемами второго и четвертого порядков точности от количества узлов. Замечание 4- При описании конвективных слагаемых разностными схемами второго и четвертого порядков точности погрешность аппроксимации может составлять в наихудшем случае задания функции источников 36,3% и 15,1% соответственно. Рис. 3. График зависимости погрешности аппроксимации операторов конвективного переноса разностными схемами от количества узлов, используемых для описания объекта: 1 — схемы четвертого порядка точности, 2 — второго
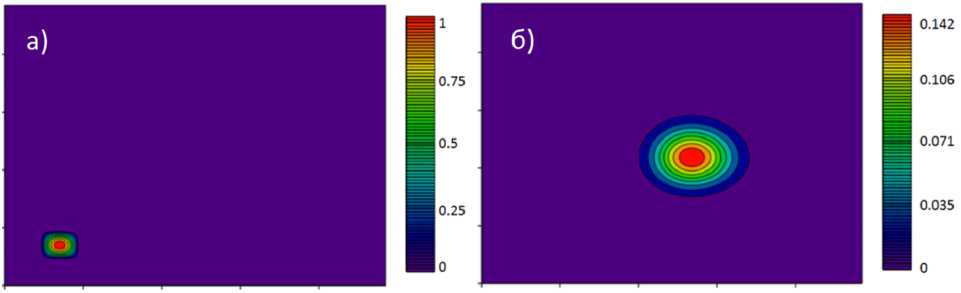
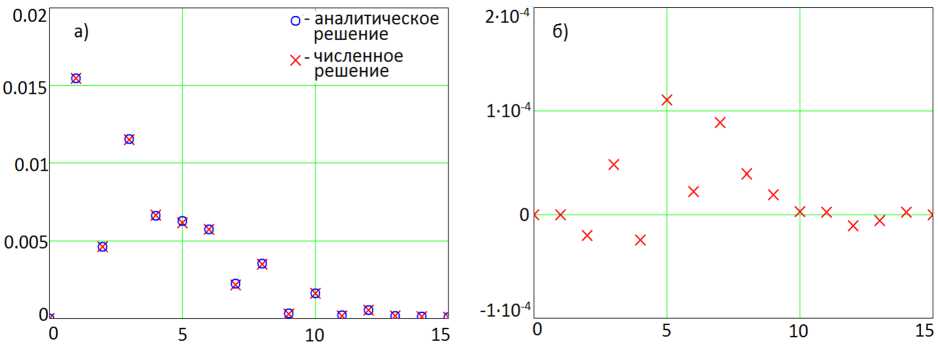
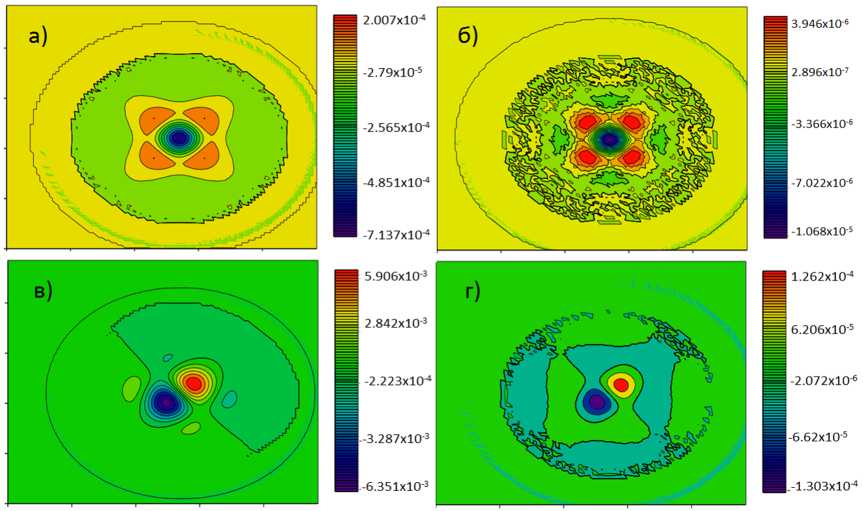
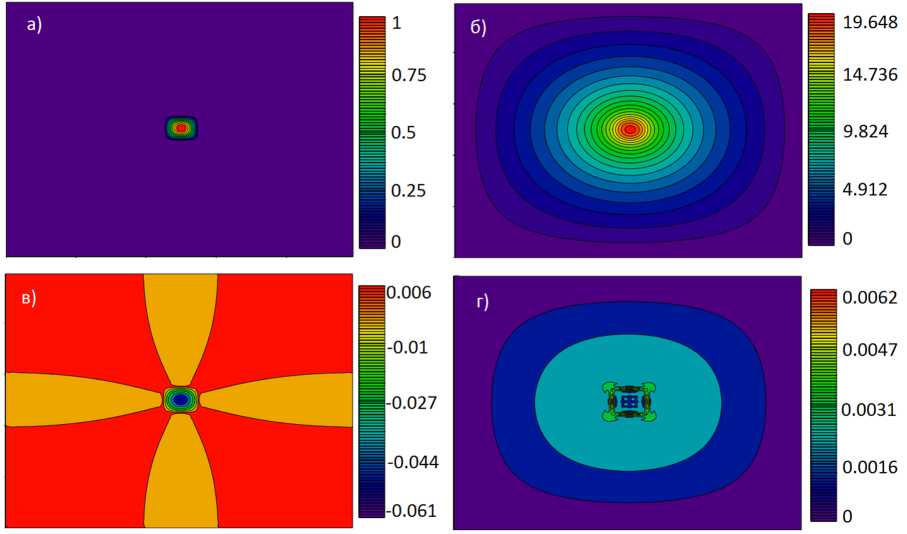
5. Сопоставление результатов расчета двумерной задачи диффузии-конвекции на основе схем второго и четвертого порядков точности Моделирование производилось на сетке размерами 100 х 100 , расчетных узлов, при этом параметры задавались следующим образом: размеры расчетной области 1х=100 м, 1у=100 м, временной интервал равен 10 с, горизонтальная составляющая равна 4 м/с, вертикальная — 3 м/с, коэффициент турбулентного обмена равен 2 м2/с. При решении задачи двумерной диффузии-конвекции начальное распределение задавалось функцией: C (х,у) = / sin (т (х — 10)) cos (т (у — 10)), {х, у} G D, D : {х G [10, 20] , у G [10, 20]} , 0, {x,y}GD. На рис. 4 приведено начальное распределение для задачи диффузии-конвекции и поле концентраций через заданный интервал времени. Замечание 5. В случае решения задачи переноса на основе разностных методов не совсем уместно говорить о точности решения исходной задачи, т.к. погрешности аппроксимации влияют на скорость конвективного переноса и даже не большие отклонения в положении решения могут приводить к большим значениям погрешности. За расчетный интервал времени вещества переносятся на 50 м. При использовании разностных методов полученные значения скорости конвективного переноса меньше реальной скорости распространения при этом отклонение положения центра области концентрации веществ для данной задачи составило 38,04 мкм. На рис. 5 приведены значения спектра поля концентрации через заданный интервал времени для аналитического и численного решения задачи диффузии-конвекции. Рис. 4. Значение концентрации в начальный и конечный моменты времени Рис. 5. Значение спектра поля концентрации через заданный интервал времени (а), разность между значениями спектра, найденные аналитическим путем и численно (б) В табл. 1 приведены значения погрешностей, зависящих от времени, для задачи диффузии-конвекции схемами второго порядка точности. Таблица 1 Зависимость погрешности от времени для задачи диффузии-конвекции Время 1 2 3 4 5 6 7 8 9 10 Максимальное значение решения 0,681 0,488 0,376 0,305 0,256 0,221 0,194 0,173 0,156 0,142 Погрешность 2,4% 2,5% 2,1% 1,7% 1,4% 1,1% 0,97% 0,83% 0,72% 0,64% Относительная погрешность 3,52% 5,12% 5,58% 5,57% 5,47% 5% 4,98% 4,8% 4,61% 4,51% В табл. 2 приведены значения погрешностей расчета задачи диффузии-конвекции на различных расчетных сетках схемами второго порядка точности, На рис. 6 приведено поле, описывающее погрешность вычислений, полученное как разность между аналитическим и численным решением для задачи диффузии-конвекции. Таблица 2 Погрешность расчета задачи диффузии-конвекции на различных сетках Размер сетки 100 X 100 200 х 200 400 х 400 800 х 800 Значение погрешности 0,6351% 0,1596% 0,04037% 0,01059% Относительная погрешность 4,507% 1,124% 0,284% 0,075% Рис. 6. Поля, полученные как разность между аналитическими и численными решениями для задачи диффузии-конвекции: сверху — задача диффузии, снизу — задача диффузии-конвекции (слева схемы второго порядка точности, справа — четвертого) Исходя из результатов расчета погрешности расчета задачи диффузии-конвекции, приведенных в табл. 1, можно утверждать, что используемые схемы не только теоретически, но и практически имеют второй порядок точности. В рассмотренной модельной задаче диффузии-конвекции область, где задано начальное распределение концентрации веществ отличных от нуля, покрывается 9 узлами по каждому из пространственных направлений. Из сопоставления результатов численных экспериментов на основе схем второго и четвертого порядков точности (рис. 6) следует, что для задачи диффузии удалось повысить точность в 66,7 раз, а для задачи диффузии-конвекции в %<5,7 раз. Результаты расчетов, приведенные на рис. 6, согласуется с теоретическими суждениями, и таким образом, при использовании разностных методов, скорости конвективного и диффузионного переносов меньше реальных скоростей данных процессов.
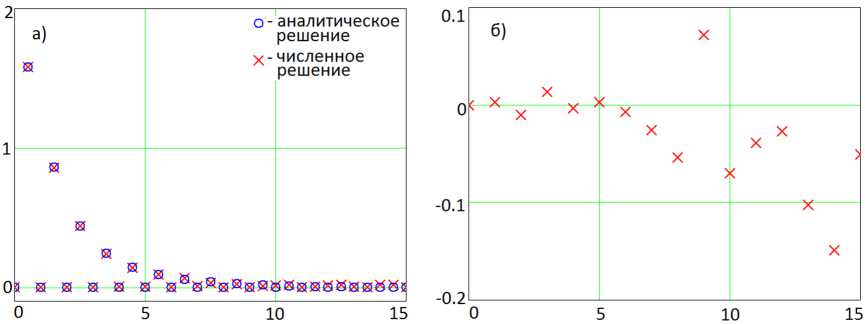
6. Сопоставление результатов расчета двумерной задачи Пуассона на основе схем второго и четвертого порядков точности Рассмотрим уравнение Пуассона [12] Au = —f, 0 < x u= N-1 N-1 / ЕЕ д mx=1 my = 1 (f) Cmx my (mx+my) ) sin(wmxx) sin(wmyy), N-1 N-1 f= Cfmysin(^mxx) sm^myy). mx=1 my = 1 Численные расчеты данной задачи производились на сетке размерами 100x100, расчетных узлов, при этом: размеры расчетной области 1х=100 м, 1у=100 м, правая часть задавалась функцией: f(x, У) = | sin (л (x — 45)) cos (л (y — 45)), 0, {x,y} G D- {x, y} G D, D : {x G [45,55], y G [45, 55]} , Аналитическое выражение соответствующее численному решению запишется: N-1 N-1 / u = ЕЕ mx=1 my=1 \ (f) Cmx my ш2 (mX (1 — f1(N/mx)) + my (1 — /x(N/my))) sin(wmxx) sin(wmyy). На рис. 7 приведены значения спектра поля концентрации через заданный интервал времени для аналитического и численного решения задачи Пуассона. Рис. 7. Значение спектра поля концентрации через заданный интервал времени (а), разность между значениями спектра, найденные аналитическим путем и численно (б) На рис. 8 представлена функция правой части (а), численное решение поставленной задачи (б) и поля, полученные как разность между аналитическим и численным решением для схем второго (в) и четвертого порядков точности (г). Следует сказать, что для двумерной задачи Пуассона схемы четвертого порядка точности для данной модельной задачи в 10 раз точнее, чем второго. Заключение В общем случае при решении прикладных задач нельзя утверждать, что повышение порядка погрешности аппроксимации гарантирует увеличение точности расчета. Из сопостав- Рис. 8. Функция правой части (а), численное решение поставленной задачи (б) и поля, полученные как разность между аналитическим и численным решением для схем второго (в) и четвертого порядков точности (г) ления результатов численных экспериментов на основе схем второго и четвертого порядков точности следует, что для задачи диффузии удалось повысить точность в 66,7 раз, а для задачи диффузии-конвекции в 1^8,1 раз, для задачи Пуассона удалось повысить точность — в 10 раз. В дальнейшем планируется внедрение разработанных схем в программные комплексы, предназначенные для расчета задач биологической кинетики на многопроцессорной вычислительной системе [13, 14]. Выполнение данных работ соответствует выполняемым в последнее время научно-образовательным программам по развитию суперкомпьютерного образования в стране [15—17]. Работа выполнена при частичной поддерэюке Задания №2014/174 6 рамках базовой части государственного задания Минобрнауки России.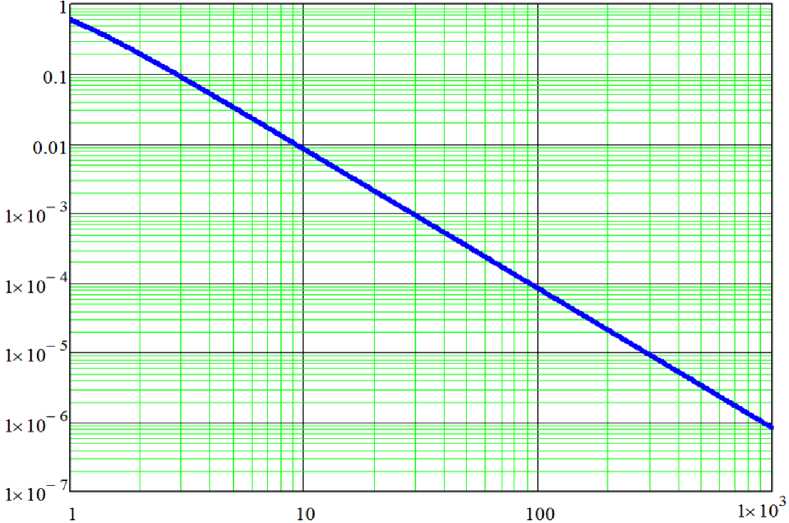
Список литературы Точность численного решения уравнения диффузии-конвекции на основе разностных схем второго и четвертого порядков погрешности аппроксимации
- Сухинов А.И., Чистяков А.Е., Семенякина А.А., Никитина А.В. Параллельная реализация задач транспорта веществ и восстановления донной поверхности на основе схем повышенного порядка точности//Вычислительные методы и программирование. 2015. Т. 16, № 2. С. 256-267.
- Чистяков А.Е., Семенякина А.А. Применение методов интерполяции для восстановления донной поверхности//Известия ЮФУ. Технические науки. 2013. № 4. С 21-28.
- Сухинов А.И., Чистяков А.Е. Параллельная реализация трехмерной модели гидродинамики мелководных водоемов на супервычислительной системе//Вычислительные методы и программирование. 2012. Т. 13, № 1. С. 290-297.
- Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. Изд-во: Лаборатория базовых знаний, 2003.
- Ладыженская О.А., Солонников В.А., Уральцева Н.Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука, 1967. 736 с.
- Пинкевич В.Т. О порядке остаточного члена ряда Фурье функций, дифференцируемых в смысле Weyl'я//Изв. АН СССР. Сер. матем. 1940. Т. 4, № 6. С. 521-528.
- Самарский А.А. Теория разностных схем. М.: Наука, 1989.
- Сухинов А.И., Чистяков А.Е., Шишеня А.В. Оценка погрешности решения уравнения диффузии на основе схем с весами//Математическое моделирование. 2013. Т. 25, № 11. С. 53-64. DOI: DOI: 10.1134/S2070048214030120
- Жалнин Р.В., Змитренко Н.В., Ладонкина М.Е., Тишкин В.Ф. Численное моделирование развития неустойчивости Рихтмайера-Мешкова с использованием схем высокого порядка точности//Математическое моделирование. 2007. Т. 19, № 10. С. 61-66.
- Сухинов А.И., Чистяков А.Е., Проценко Е.А. Математическое моделирование транспорта наносов в прибрежной зоне мелководных водоемов//Математическое моделирование. 2013. Т. 25, № 12. С. 65-82. DOI: DOI: 10.1134/S2070048214040097
- Сухинов А.И., Чистяков А.Е., Проценко Е.А. Математическое моделирование транспорта наносов в прибрежных водных системах на многопроцессорной вычислительной системе//Вычислительные методы и программирование. 2014. Т. 15, № 4. С. 610-620.
- Владимиров В.С. Уравнения математической физики. М.: Наука, 1988.
- Сухинов А.И., Никитина А.В., Чистяков А.Е., Семенов И.С. Математическое моделирование условий формирования заморов в мелководных водоемах на многопроцессорной вычислительной системе//Вычислительные методы и программирование. 2013. Т. 14, № 1. С. 103-112.
- Сухинов А.И., Никитина А.В., Чистяков А.Е. Моделирование сценария биологической реабилитации Азовского моря//Математическое моделирование. 2012. Т. 24, № 9. С. 3-21.
- Антонов А.С., Артемьева И.Л., Бухановский А.В., Воеводин В.В., Гергель В.П., Демкин В.П., Коньков К.А., Крукиер Л.А., Попова Н.Н., Соколинский Л.Б., Сухинов А.И. Проект "Суперкомпьютерное образование": 2012 год//Вестник Нижегородского университета им. Н.И. Лобачевского. 2013. Т. 1, № 1. С. 12-16.
- Воеводин В.В., Гергель В.П., Соколинский Л.Б., Демкин В.П., Попова Н.Н., Бухановский А.В. Развитие системы суперкомпьютерного образования в России: текущие результаты и перспективы//Вестник Нижегородского университета им. Н.И. Лобачевского. 2012. Т. 4, № 1. С. 268-274.
- Антонов А.С., Артемьева И.Л., Бухановский А.В., Воеводин В.В., Гергель В.П., Демкин В.П., Коньков К.А., Крукиер Л.А., Попова Н.Н., Соколинский Л.Б., Сухинов А.И. Проект "Суперкомпьютерное образование": 2012 год//Научный сервис в сети Интернет: поиск новых решений. Труды Международной суперкомпьютерной конференции. Москва, 2012. С. 4-8.


