Точность местоопределения излучателей последовательностей сверхширокополосных импульсов в триангуляционных системах

При определении местоположения сверхширокополосных (СШП) источников радиоизлучения триангуляционным способом [1] оценка их угловых координат осуществляется по разности времени прихода сигналов (ВПС) в пространственно разнесенных точках [2]. Базовый комплект угломерной системы [1] включает в себя два пеленгаторных поста и пункт сбора и обработки пеленговой информации, связанные линиями передачи данных [1]. Каждый пост выполняется в виде двухпозиционной подсистемы синхронизированных приемников-измерителей ВПС с пунктом сбора и обработки результатов измерений [2]. Местоположение объекта характеризуется координатами точки пересечения лучей, построенных из центров пеленгационных баз [2].

В [2] в приближении равенства дисперсий оценок максимального правдоподобия [3] и высокой апостериорной точности регистрации разности моментов ВПС в приемниках с гипотетическими диапазонными всенаправленными антеннами найдена среднеквадратическая ошибка (СКО) местоопределения СШП изотропных излучателей.

Однако ввиду технической сложности генерации мощных СШП-сигналов [4; 5] для их передачи-приема, как правило, применяются апертур- ные антенны с высокими показателями направленности в диапазоне частот [6; 7] и антенные решетки, выполняющие синхронное сложение излучений отдельных элементов в пространстве [5; 8].

Согласно [6; 8], парциальные коэффициенты усиления (КУ) таких антенных систем в общем случае не могут быть представлены произведениями угловых и частотных распределений. Поэтому форма и частотно-временные параметры сигнала на входе приемника-измерителя зависят от направления на его источник, типа и электрических размеров передающей и приемной антенн [9; 10]. Дисперсия оценки ВПС, как показано в [9], обратно пропорциональна значению интеграла от произведения спектральной плотности энергии излучателя и парциальных КУ антенн в эквивалентной полосе циклических частот [6] перехватываемого волнового процесса; ее значения в каждой точке пространства различны [9; 10].

В предлагаемой работе с использованием спектрального энергетического уравнения прямого радиоканала [6] для расчета энергии негармонических сигналов на входах пространственно разнесенных приемников найдены СКО оценок координат источников регулярных последовательностей СШП-импульсов, для излучения и перехвата которых применяются плоские апертурные антенны и линейные антенные решетки.

Цель работы – анализ влияния характеристик передающих и приемных антенных систем на точность оценки координат объектов.

Для задания позиций приемников-измерителей ВПС введем декартову систему координат XOY , а для определения местоположения источника радиоизлучения – полярную систему координат ( р, 9 ) , начало которой совпадает с точкой O .

Будем полагать, что i -й приемник-измеритель ВПС ( i = 1, 2), входящий в состав к -й пеленгационной подсистемы ( к = 1, 2), размещается на оси Ох в точке х кi ) = ( -1 ) ^к d/ 2 + ( -1 ) i L/ 2, где d – база системы местоопределения, L – пеленгационная база ( L << d ); границы базы системы местоопределения совпадают с центральными точками Х к = ( -1 ) ^к d] 2 пеленгационных подсистем ( к = 1, 2). Положение излучателя задается радиус-вектором с абсолютной величиной | р | = R o , отклоненным от оси Оу по часовой стрелке на угол 9 = 9 o .

Собственные шумы приемников представимы гауссовским белым шумом с односторонней спектральной плотностью мощности N ₀; передаточные функции входных усилительных каскадов являются постоянными в полосе рабочих циклических частот toe [ to min ; to max ] . Парциальные КУ антенн излучателя и приемников обозначим G т ( to, 9 ) и G r ( to, 9 ) соответственно.

Излучаемая СШП-последовательность характеризуется средней мощностью P _S, числом N _S и периодом следования Т _S импульсов. Величина Т _S значительно превышает время автокорреляции импульсов [6] и в процессе измерений является известной; спектр последовательности сосредоточен в полосе рабочих циклических частот приемников.

При R0 >> L, когда СКО измерения разности хода сигналов между точками приема значительно меньше базы системы местоопределения и подсистемы пеленгования, дисперсия триан- гуляционной оценки координат объекта имеет вид [1]

2R02

’r   л2   2    E’9к , d cos 9 0 k=1

где

=2к=-тЛ   E’2«(2)

L cos ⁹ o к i = 1

– дисперсия оценки направления прихода arctg

R o cos 9 o _v R _o sin 9 0 + ( -1 ) ^{к +1} d /2 ,

⁹ 0 к

при R o sin9 o + ( -1 ) ^{к +1} d /2 > 0;

< п - arctg

R o cos 9 o

R _o sin 9_o + ( -1 ) ^{к +1} d / 2

при Rosin9o + (-1)к+1 d/2 < D сигнала относительно центра k-й пеленгационной базы (к = 1, 2), ’2к — дисперсия измерения ВПС i-м приемником (i = 1, 2) к-й пеленгационной подсистемы (к = 1, 2), с — скорость света.

Точность оценки максимального правдоподобия времени прихода регулярной последовательности импульсов с известным значением Т _S определяется выражением [10]

’ t ki

8 п N _o Г R _o ^ 2 [^ к *⁽ d ’ L ’ R ^o, ^{9 o} ) ]

^N S ^; S ^ I“J    5 ⁽ к ) ( d , L , R o , 9 o ) , ⁽⁴⁾

к = 1,2, i = 1,2, где

^⁽ к ) ( d , L , R o , 9 o ) =

1 + ( -1 ) ^kd + ( -1 ) i L

R 0

sin 9 o +

+

(-1) к d + (-1) i L v

– геометрический фактор, характеризующий взаимное расположение источника СШП-сигна-лов и приемников системы местоопределения,

5(к) (d, L, Ro, 9o) =-------1

^to max ^to min

^max(9к )

x J     G T (to, 9( к)) GR (to, 9( к)) dto, n mm(e( к))

– эффективный момент передачи СШП-сигнала в прямом радиоканале [6] от излучателя к i-му приемнику (i = 1, 2) к-й пеленгационной подсистемы (к = 1, 2), усредненный в полосе циклических частот to e [to.    ; to ], mn max

9⁽ i )

⁹ o к

arctg( R o cos 9 o / [ R o sin 9 o + + ( -1 ) ^{к +1} d /2 + ( -1 ) i ⁺¹ L /2]) при R o sin 9 o + ( -1 ) ^{к +1} d /2 +

< + (-1)i+1 L/2 > o;

п - arctg( R o cos 9 o / [ R o sin 0 o + + ( -1 ) k ⁺¹ d /2 + ( -1 ) i ⁺¹ L /2]) при R o sin0 o + ( -1 ) k ⁺ 1 d /2 +

+ ( -1 ) i ⁺¹ L/ 2 < 0

– направление на излучатель из позиции с координатами ( x ki ) ; 0), Q min (0⁽ k ) и Q max (0⁽ к ⁾) — нижняя и верхняя границы эквивалентной полосы

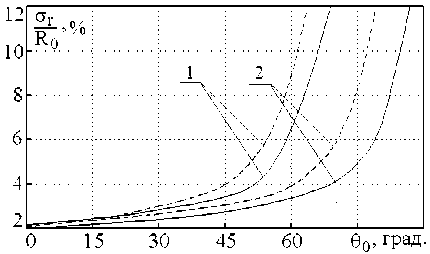
Рис. 1. Зависимости СКО пеленгования источника последовательности СШП-импульсов при использовании для их излучения и приема апертурных антенн

циклических частот радиоканала передачи сигналов к г -му приемнику ( г = 1, 2) к -й пеленгационной подсистемы ( к = 1, 2), удовлетворяющие уравнению [10]

Q      ( fl(г)                (г)

^Q max ( ⁰ к I ^Q min ( ⁰ к ) =

x

да

J GT (to, 0(к)) GR (to, 0(к)) dto

-да

max to

Gt (to,0( к’) Gr (to,0( к’)

и условиям [9]:

min Q

0⁽ к )

( i ) min ( ⁰ к )

min ,

max ^Q m _a x ( ^{0 (} i .’ ) < ^to m _a x 0⁽ к            ^{[ ;}

Из (4)–(6) следует, что дисперсия оценки времени прихода регулярной последовательности СШП-импульсов снижается пропорционально увеличению значения интеграла от произведения парциальных КУ антенн излучателя и приемника в пределах эквивалентной полосы циклических частот радиоканала. При совпадении диапазонов рабочих циклических частот излучателя и приемника эффективный момент передачи сигналов в радиоканале, согласно (6)–(9), равен произведению парциальных КУ их антенн, усредненному в полосе циклических частот to е [ to. ; to.     ] .

mn max

В соответствии с (6) имеем, что при большом периоде следования, позволяющем осуществлять линейное накопление импульсов в приемнике [9; 10], СКО оценки времени прихода по-

следовательности снижается пропорционально

N _S, как при приеме узкополосных сигналов [11], вне зависимости от углового положения излучателя и парциальных КУ антенн.

Из (1)–(8) с учетом (9) находим дисперсию оценки координат источника регулярной последовательности СШП-импульсов

2 =  8 п No r  NSPSTS

^R 0

L d cos 0 o

x

x

x

I*+ к=1

cos 0 o

^ sin 0_o + ( -1 ) ^{к +1} d /2 R _o

I [ 5 ⁽ i ) ( d , L , R o , 0, i = 1

Г 1 + (-!) d + + (-1) iL

R 0

x

- 1

x

sin 0 o +

'(-1) kd + (-1) iLf"

⁺        2 R_o

<            o 7

На основе (10) с учетом (6) проведен анализ точности местоопределения источников последовательностей СШП-импульсов, излучаемых

и перехватываемых плоскими апертурными антеннами и линейными антенными решетками.

Парциальный КУ плоской апертурной антенны с радиусом раскрыва a _T,R, удовлетворяющим условию to min a t r / c ^ 5, при котором ее коэффициент полезного действия значителен [12], определяется выражением [6]

G T, R

(to, 0) = sinc2

^to а T,R

2 cR _o

₂ '0^ ₂ | ^to a T R | x ctg ²      J 2       ,— sin 0 ,

12 7 1 I с J

x

где J 1 ( ^ ) — функция Бесселя первого рода первого порядка, sinc ( x ) = sin ( x)/x .

Путем подстановки (11) в (6) и (8), а полученных результатов в (10) с учетом (7) найдем дисперсию оценки координат СШП-излучателя при использовании для передачи и перехвата сигналов плоских апертурных антенн. Итоговое выражение не приводится ввиду громоздкости.

На рис. 1 представлены зависимости СКО оценки координат от углового положения источника СШП излучения, рассчитанные при B min a r / c = 5 (пунктирная линия) и to min a r / c = 1o (сплошная ли-

ния), to / to.    = 4 (кривая 1) и to / to = 6

max mn              max mn

(кривая 2), а также P s T s / N о = 90 дБ, to min a _T / / c = 5, L /( cN _S T _S) = 0,2, d / L = 5, R ₀ / d = 10.

Из анализа приведенных результатов следует, что СКО местоопределения объекта убывает по мере уменьшения угла 00 вследствие увеличения доли энергии сигнала, перехватываемой по главному лучу энергетической диаграммы направленности [5; 6] передающей антенны. Увеличение радиусов раскрывов приемных антенн также приводит к повышению точности выполняемых измерений по закону, близкому к линейному, за счет возрастания парциальных КУ.

При одинаковых габаритах антенных систем меньшая СКО оценки координат достигается для источников радиоизлучения с большим значением верх-ней границы полосы циклических частот, а при to min a т r / c > 5 и фиксированном отношении tomax / tomin — для излучателей с большим значением tomin, поскольку высокочастотные компоненты спектров сигналов характе- ризуются меньшими потерями энергии при рас- пространении в радиоканале [6; 7].

Парциальный КУ линейной решетки из N _T,R элементарных электрических диполей с шагом d _T,R имеет вид [6]

G T, R ( to, 0 ) = 2 sin²0

F T, R ^(to , ^{0) Ф} T, R ^(to)

где sin2

F T, R ^(to , ⁰⁾ =

^to N T,R ^d T,R    „

-------------cos 0

2 c

₂ Г to d sin² ----

T,R ----cos 0

2 c

,

П

Ф T, R ( to ) = J F t, _R ( to, 0 ) sin³0 d 0 .

В результате подстановки (12) в (6) и (8), а полученных соотношений в (10) с учетом (7) определена точность оценки местоположения СШП- источников радиоизлучения при использовании в них и приемниках-измерителях ВПС указанных антенных решеток.

На рис. 2 представлены зависимости СКО ме-стоопределения объекта от направления прихода импульсов при to min d tr / c = 2, N tr = 5, ^to max / ^to min = ^{4 (кривая} 1) ^{и to} max / ^to min = ^{6 (кри}вая 2). Отношения излучаемой энергии к одно с торонней спектральной плотности мощности собственных шумов приемников-измерителей ВПС, размеров пеленгационных баз к пространственной

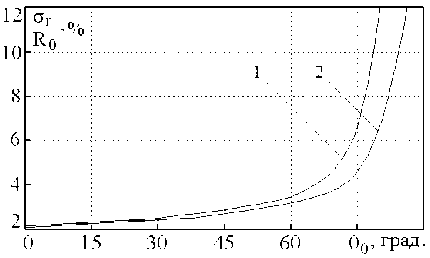
Рис. 2. Зависимости СКО пеленгования источника последовательности СШП-импульсов при использовании для их излучения и приема линейных антенных решеток

длине последовательности, а также характеристики взаимного расположения объекта и постов системы местоопределения выбраны такими же, как при получении зависимостей на рис. 1.

Из представленных результатов следует, что при увеличении to _max в 1,5 раз СКО оценки координат СШП-излучателя в секторе углов 0 0 е [30°; 60°] снижается в 1,2...1,6 раз.

Уменьшение точности выполняемых измерений наблюдается при углах, удовлетворяющих условию to N T,R d T,R     n(i)    ,

------,     , cos 0   << 1, 2c             k вследствие малой доли излучаемой энергии и низкой эффективности ее перехвата решетками приемников-измерителей. Малая точность ме-стоопределения объектов также характерна для угломерных систем, оснащенных решетками с малым числом и высокой плотностью размещения элементов, когда to NR dR << 1

2c и максимальное значение КУ, как показано в [9], стремится к 1,5.

Установлено, что при увеличении числа элементов решеток приемников-измерителей ВПС до N r = 10 или шага до to min d r / c = 3,2 погрешность местоопределения излучателя с коэффициентом перекрытия полосы рабочих циклических частот to_max / to min = 4 в секторе углов 0 0 е [30°; 60°] снижается в 1,3 раз.

Таким образом, с использованием спектрального энергетического уравнения прямого радиоканала для расчета энергии негармонических сигналов на входах пространственно разнесенных приемников вычислены СКО оценок максимального правдоподобия координат источников регулярных последовательностей СШП-импуль- сов в триангуляционных системах с учетом направленных свойств передающих и приемных антенн. Проведен анализ точности местоопреде-ления излучателей при применении в них и измерительных приемниках плоских апертурных антенн и линейных антенных решеток с различными электрическими размерами и полосами рабочих циклических частот.