Точность обработки отверстий с использованием переносных устройств

с использованием переносных устройств и станков. В настоящей работе рассматривается влияние сил резания и жесткости технологической системы на точность обработки отверстий с использованием переносных устройств с подвижной сверлильной головкой.

При обработке отверстий сверлением, зенкерованием, развертыванием возникают упругие отжатия технологической системы, вызывающие разбивку и изменение формы отверстия в поперечном и продольном сечениях. Акцент в работе сделан на сверление – как процесс, при котором возникают наибольшие силы резания и наибольшая неточность обрабатываемого отверстия. На систему «станок – инструмент» действуют [1] сила подачи, вызывающая равнодействующую силу P 0 – осевое усилие, крутящий момент, оказывающий влияние на тангенциальные составляющие режущих кромок сверла R z1 и R z2 , и неуравновешенная радиальная сила ∆ P y = P y1 – P y2 . Отжим конца сверла и системы в целом происходит именно под влиянием силы ∆ P y , смещающей режущие кромки сверла относительно оси вращения, что является причиной увеличения диаметра (разбивки) и изменения формы отверстия при сверлении. Появлению такой силы являются неравномерность главных режущих кромок, смещение поперечной режущей кромки и различные углы в плане у сверла. По экспериментальным данным, полученным на переносных устройствах, приближенное значение неуравновешенной радиальной силы можно определить следующей зависимостью:

ΔPy ≈0,0185(1-f)PO где f - отношение осевого усилия, действующего на поперечную кромку спирального сверла к усилию подачи /0,5).

Осевое усилие P 0 также оказывает влияние на изгиб сверла. Его можно рассчитать по формуле:

PO = 10 • CP • d • sy • KP • KO,

где C p - коэффициент; q, y - показатели степени; d - диаметр сверла, мм; s - подача, мм/об; K p - коэффициент, зависящий от обрабатываемого материала заготовки; K 0 - коэффициент, зависящий от влияния режущих кромок и ленточек.

Технологическую систему переносного устройства с подвижной сверлильной головкой (ПСГ) можно представить как двухпролетную балку разных сечений по длине (рис. 1.).

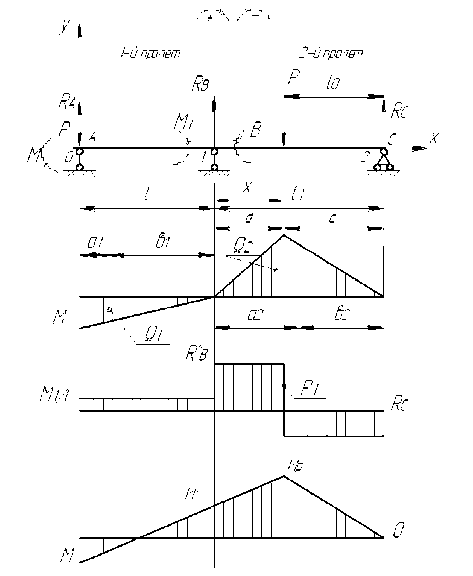
Рис. 1. Схема для определения прогиба в системе с ПСГ

Такая система является один раз статически неопределимой [2]. Опоры нумеруются следующим образом: опора в точке A -опора 0; в точке B - опора 1; в точке С - опора 2. Участок AB - первый пролет, участок BC -второй пролет. Начало координат в точке A . Входные данные технологической системы следующие: P = AP y - неуравновешенная радиальная сила; P 1 - сосредоточенная сила -вес подвижной сверлильной головки (ПСГ); М

- момент на режущих кромках от осевого усилия, М = P 0 d /2, где P 0 - осевое усилие, d - диаметр режущего инструмента; l - длина вылета режущего инструмента от шпинделя; l 1 - расстояние между опорами направляющих; x -переменная величина перемещения равная длине обработки, то есть толщине заготовки - x_max = H . Величина x изменяется от правого положения в левое к опоре 1 с значения x_max = H к x =0, то есть x ^ 0.

Для пролетов строятся эпюры моментов и сил (рис. 1.). Так как данная система является один раз статически неопределимой, то уравнение трех моментов записывается один раз для промежуточной опоры 1 [2]:

М _о • l + 2 М , ( l + L ) + M ₂ • L = - 6(^1- + ^{Q 2} • b ² ),

0    112 1    i i где Q1 - площадь эпюры от заданной нагрузки на первом пролете: Q1=М l/2, Q2 - площадь эпюры на втором пролете: Q2=P1lox/2, a1 и b2 -расстояние центров тяжести указанных площадей от левой и правой опор своего пролета: ai=l/3 и b2=(2li - x)/3

M0 = MA = -M, M2 = MC = 0.

После подстановки в выражение (2) приведенных данных оно примет вид:

- m • l + 2 M , ( l + l 1 ) = - 6 •

^{< 1} Ml • ¹ 1 2     3

l

1                       i

-P 1 • l 0 • x • -(2^ - x )

+ "-------/ ------- l1

Из выражения (3) определяется момент в опоре 1:

_М =- P • 1 0 • x (2 l 1 - x )

¹            2 • l 1 ( l + 1 1 )

Для построения окончательных эпюр M и Q для каждого пролета выполнены расчеты (здесь они опущены), которые имеют следующие значения:

М + М.  _

Ra =       " P

.

M A (0) = - М , M A ( l ) = R A • l + P • l - M = M 1 .

_ P 1 • 1 0 M 1 ( l + 1 1 )        P_xx + M 1

Rd =---R = -----

^B l           l • l 1          C         l 1

M P

P1 ₀( 1 1 - 1 0 ) + M 1 • 1 ₀

d ² у dx

—1— [- MX0 + RAX - PX Eu • Jи

Для составления дифференциального уравнения упругой линии системы необходимо определить изгибающий момент технологической системы, который можно представить следующим выражением [2]:

M ( x ) = R A ( 1 + 1 ₁ ) - M ( 1 + 1 ₁ ) ⁰ - P ( 1 + 1 ₁ ) +

+ R_r (L + x ) + M, (L + x ) ⁰ - PL B 0             1X0             10

.                                                (4)

Дифференциальное уравнение упругой линии системы имеет вид:

= тЧ-С R A ( 1 + 6) - M ( ¹ + O" - P ( ¹ + 1 1 )) + dx    E u • J и

-4-( M 1 ( 1 0 + x )⁰ + R b ( 1 0 + x ) - P • 1 1 )

E • J

,                                                (5)

где E u - модуль упругости режущего инструмента; J u - момент инерции инструмента; Е -модуль упругости направляющих, по которым перемещается сверлильная головка; J - момент инерции направляющих. Проинтегрировав выражение (5) дважды, получится уравнение упругой линии системы следующего вида:

Данное уравнение интегрируется один раз и получается уравнение угла поворота:

— = 0_O ( x ) = —¹— dx ° E u • J и

- Mx +

R a x ²

PX1

+ C

Для балки на двух шарнирных опорах прогибы на этих опорах равны нулю: при X = 0 у (0) = 0 ^ у 0 = 0 ; при X = 1 у ^{( 1} ) = ⁰ ^ y A = У в = У с = 0 .

Уравнение прогиба пролета 1:

у (1) = ©• 1 +

E • J и

M1 ² R 1 ³ P1 ³

--+ —

2     6     6

Из этого выражения находится значение 0 ₀ :

1     .P • 1 ² 2 M1 M. • L

( + ¹)

E u • J и    3      6      6 ⁷

Подставив в уравнение (6) значения у₀ и ⁰ 0 , получится уравнение отжатия технологической системы устройства с ПСГ для любого участка в пределах изменения x :

у ( x ) = у 0 + 0 • x +

E • J ии

R A ( 1 + 1 1 )   M ( 1 + 1 1 )²

6           2

P ( 1 + 11f

у ( x ) =

1 P • 1²

Eu • Jи (”

+

2 M1

M 1

-)( 1 + 1 1 ) +

1 R A ( 1 + 1 1 )³ M ( 1 + 1 1 )² P ( 1 + 1 1 )³

EE?Jr_u [ ”6      2

+

E • J

M 1 ( 1 0 + x )²    R . ( 1 0 + x )³    P 1 • 1 3

2            6         6

+

E • J

M 1 ( 1 0 + x )²    R b ( 1 0 + x )³ P • 1 0 ³

2            6         6

Начальные параметры прогиба у₀ и угла поворота 0 можно определить по первому пролету. Дифференциальное уравнение пролета 1 имеет вид:

Уравнение (9) можно преобразовать, введя в него значения M 1 , R A , R B и M . После преобразования формула отжима технологической системы устройства с подвижной сверлильной головкой имеет вид:

у ( ^x ) =

_____ 1

E u • J.

P ₀ • d • 1 ₁( 1 + 1 ₁) • ( 1 ₁ - 1 ) P1 ₁ ( 1 + 1 ₁) • (2 1 - 1 ₁)

12 • 1

P • 1 ₀ • x (2 1 ₁ - x ) • (2 1 - 1 ₁)

+

12 • 1

( 1 0 + x )³ • (2 l • 1 1 + 1 1 x - x ²) - 2 1 0 • l • 1 2

₊ p • i 0 •                    3ы.

• ⁴ • E • J    x (2 l i ^- x ) • ( l 0 + x ⁾²

_         l 1 ( l + 1 1 )

По полученной формуле проведены вычисления изменений формы отверстия по длине при сверлении с введением в неё тех же параметров, что и при проведении экспериментов. Эта формула также применима и к переносным сверлильным станкам с подвижной сверлильной головкой.

Эксперименты по исследованию влияния различных факторов процесса сверления на точность отверстия проводились с использованием переносного устройства с подвижной сверлильной головкой типа УСЭ047, разработанного и изготовленного в НИЛ вуза. В результате проведенных экспериментов выявлено отклонение формы отверстия по длине от цилиндричности [3]. Характер изменений формы отверстия по его длине вычисленных по формуле (10) и полученных по результатам экспериментов представлен кривыми (рис. 2).

Как видно по кривым (рис. 2) форма отверстия седлообразная с максимальным диаметром на входном торце и минимальным – на выходном торце и сужением (образованием горловины) к середине длины. Теоретические вычисления подтверждают закономерность изменения формы отверстия по его длине и не занижают погрешность от разбивки по диаметру в сравнение с действительными значениями. По формуле (10) можно также производить расчеты погрешности обработки отверстий при зенкеровании и развертывании, для которых значения сил P и P 0 рассчитываются по соответствующим формулам. Для переносных станков и устройств, имеющих направляющие втулки для инструмента, вылет режущего инструмента в формуле (10) принимается равным расстоянию от выходного торца втулки до поверхности заготовки.

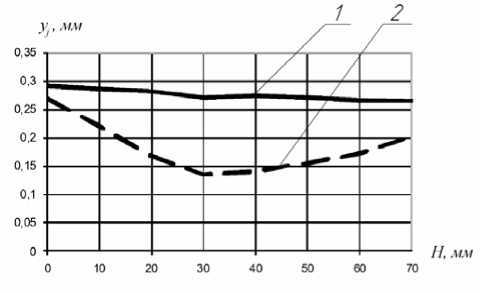
Рис. 2. Кривые формы отверстия в продольном сечении: 1 – теоретическая кривая; 2 – фактическая кривая