Точность оценки местоположения источников последовательностей сверхширокополосных импульсов в дальномерных системах

Оценка координат мобильных объектов при дистанционном контроле и управлении движением [1] осуществляется по результатам обработки сигналов бортовых ответчиков на запросы радиолокационных постов наблюдения (РПН). Для обзора пространства в широких секторах углов РПН оснащаются слабонаправленными антеннами [1; 2]; помехоустойчивость управления достигается за счет применения запросных и ответных сигналов в виде последовательностей сверхширокополосных импульсов [3].

Местоопределение СШП-источников радиоизлучения (ИРИ) в РПН осуществляется дальномерным методом; положение объекта характеризуется координатами точки пересечения лучей, построенных из позиций не менее чем двух разнесенных в пространстве приемников-измерителей времени прихода сигналов [2].

Как показано в [4], дисперсия оценки максимального правдоподобия времени прихода СШП-сигнала [2; 3] обратно пропорциональна значению интеграла от произведения спектральной плотности излучаемой энергии и парциальных коэффициентов направленного действия (КНД) передающих и приемных антенн в эквивалентной полосе рабочих частот приемника [5]. При этом форма обрабатываемых импульсов, зависящая от направления на их источник, типа и электрических размеров антенн РПН [6], в общем случае является различной на входе каждого измерителя [4].

В предлагаемой работе с использованием частотно-угловых характеристик передачи–приема негармонических сигналов [5; 6] найдена дисперсия оценки местоположения источников регулярных последовательностей СШП-импульсов в дальномерных системах с плоскими апертурными антеннами при нормативных ограничениях на уровень излучаемой мощности [1; 7].

Цель работы – исследование точности мес-тоопределения объекта с учетом направленных свойств его антенны и антенн приемников-измерителей времени прихода сигналов.

Для позиционирования приемников РПН введем декартову систему координат XOY ; для оценки местоположения ИРИ – полярную систему координат ( р, 9 ) , начало которой совпадает с точкой O .

Будем полагать, что приемники-измерители времени прихода сигналов располагаются на оси Ox в точках х ^ = ( -1 ) k L 2, ( к = 1, 2), где L – база измерительной системы [2]. Положение излучателя характеризуется радиус-вектором с абсолютной величиной |р | = R о , отклоненным от оси Oy по часовой стрелке на угол 9 = 9 о .

Собственные шумы приемников представимы гауссовским белым шумом с односторонней спектральной плотностью мощности N0; передаточные функции входных усилительных каскадов являются постоянными в полосе рабочих циклических частот to е I to ; to I . Антенны ИРИ min max и измерительных приемников имеют плоские апертуры в форме кругов с радиусами aT и aR соответственно, удовлетворяющими условию max(ат, aR) << L. В качестве частотно-угловых © С.Н. Разиньков, 2013

характеристик передачи-приема СШП-сигналов по аналогии с [4–7] будем использовать парциальные КНД этих антенн Gt ( ю, 9 ) и Gr ( to, 9 ) .

Излучаемая СШП-последовательность характеризуется числом N_s , периодом следования T_s и средней мощностью P_s импульсов. Для однозначного определения координат объекта [1] и накопления принимаемой энергии по линейному закону [3] величина T_s значительно превышает время автокорреляции импульсов [4; 7].

При R ₀ >>  L дисперсия местоопределения излучателя в дальномерной системе имеет вид [2]

да

J GT (ю , 9к ) GR (ю , 9к )dю

—да

max к GT (ю , 9 к ) GR (Ю , 9 к ) ю min Q min(9к ) = юmin,

6 к max Q max(9к ) =юmax.

9 к

Из (1)–(4) с учетом (5), (6) находим дисперсию

местоопределения излучателя последователь-

ности СШП-импульсов:

° R =

^f C ^R о

_А ²

L cos 9n k ⁰ 7

Z° 2k k=1

° R =

^{8 п}_ N о      ^R о

N s P s T s к L cos 9 _{о ?}

Z к=1

& ( L , R о , 9 о )

S k ( L , R о , 9 о ) .

где о 2 k — дисперсия измерения времени прихода сигнала в к - м (к = 1, 2) приемнике; с — скорость

света.

Согласно [4], при оценке времени прихода регулярной последовательности СШП-импульсов

методом максимального правдоподобия [8]

чина о 2 k определяется выражением

₂    8п N _о f R о А 2 &  ( L , R о , 9 о )

О =                                      х,

N s P s T s k c 7 S k ( l , R о , 9 о )

вели-

к = 1,2, где

Sk (L, Rо, 9о> Sk (9к) =

х

® max

—

^ю min

Q mk ax ( 6 к )

х J Gt (ю, 9к ) Gr (ю, 9к )dю, q m in(e к)

^ к ( L , R о , 9 о ) =

¹ + ( ^—1 ) k-L - sin ⁹ о ⁺ R ₀

f 7    2

2 R

к о 7

– геометрический фактор, характеризующий взаимное расположение источника и к -го ( к = 1, 2) приемника сигналов,

⁹ к = arctg

R 0cos 9 о к R о sin 9 о +(—1)к—1 L/2 7

– направление на излучатель из позиции k -го ( ^к =1,2) измерителя, ^Q min ( ⁹ к ) и q max ( ⁹ к ) ^- нижняя и верхняя границы эквивалентной полосы циклических частот обрабатываемого сигнала, удовлетворяющие уравнениям [6]:

Qmmax(9к ) —Qmmin(9к ) =

Согласно (7), при максимально допустимом нормативными ограничениями уровне излучаемой мощности точность оценки координат СШП-излучателя возрастает пропорционально значению интеграла от произведения парциальных КНД передающей и приемных антенн в эквивалентной полосе рабочих частот приемника. Среднеквадратическая ошибка (СКО) местооп-ределения о r источника последовательностей CШП-импульсов с периодом следования, значительно превышающим время их автокорреляции, снижается по сравнению с показателем, достижимым при обработке одиночного сигнала, в N_s раз [3].

Для достижения высокой точности оценки времени прихода и координат источников СШП-сиг-налов требуется применять антенны с равномерным распределением КНД в эквивалентной полосе циклических рабочих частот ю е ^to min ; to_max J . При местоопределении излучателя импульсов с высокой крутизной огибающей и малой шириной спектра могут быть использованы узкополосные антенны с высокими КНД Gr ( ю, 9 к ) в области максимума Gt ( ю, 9 к ) , к = 1, 2.

Парциальный КНД плоской апертурной антенны с нормированным радиусом раскрыва ю min a т R / c - 5 в приближении физической оптики имеет вид [5]

G T , R ^(ю,9 к ) = ^v T , R ^{(ю) ctg}2 к ""I" 7 ^х

Iю a               I х J2     T,R sin 9к , к = 1,2,

I с                   )

где V т r ( ю ) — парциальный коэффициент ис-

пользования поверхности антенны, который при

R 0

>> max ( а т , a R )

определяется выражением [7]

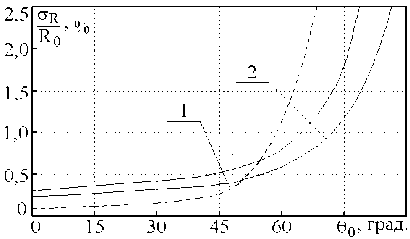
Рис. Зависимости нормированной СКО местоопределения излучателя СШП-импульсов от его углового положения

При передаче-приеме сигналов электрически малыми антеннами, а также при перехвате излучений по главному лучу энергетической диа-

граммы направленности антенны, когда

f to a Г D I to a T D

J       T^^- sin 9 «---- T i ^ sin 9 ,

¹V с 7      2 с

выражение (8) преобразуется к виду [5]

G T , R

( ^to, ⁹ k )

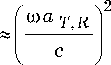
4 cos

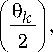
vт r (to) ® sinc2

to а т , R --—

2 cRn

V 0 7

k = 1,2.

J 1 (...) — функция Бесселя первого рода первого

Подставляя (11) в (3), а полученный результат последовательно в (2) и (1), при to max / to min >> 1

находим

порядка.

В результате подстановки (8) с учетом (9) в

c R=

(3), а полученного результата с учетом (4)–(6)

80 n N о

N s P s T s ( a T a R L cos 9 о

последовательно в (2) и (1) получим

CR =

8 П N 0 ( to max -to min ) f R ² V

N s P S T s         L cos 9 о ₇

x

k = 1

^ k ( L , R о , 9 о )

4 cos

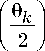
x£ ^k (L, R0, 9о )tg4 9 I X k=1                         V 2 7

" й mm _ax ( 9 _fc )

/ J

L « _in ( 9 _k )

to ат

c

sin 9 _k

sinc2

^{to а}Т

x sinc2

^{to a}R

2 cR n V7

2 cR n

V 0 7

I to aR . I .

J 2       sin 9 k d to

1 c

На рисунке приведены найденные с использованием (10) зависимости нормированной СКО местоопределения ИРИ c r/R о от его углового положения 9 о при to min а т / c = 5, R о / L = 10, L /( cT s ) = 0,2 и P_ST_S / N о = 90 дБ. Сплошными линиями представлены результаты, полученные для приемных антенн с нормированными радиусами раскрывов to min a R / c = 5, штриховой линией — для антенн с to min a R / c = 10; зависимости 1 рассчитаны при to _max / to min = 4, зависимость 2 — при to / to = 6.

max min

Из их анализа следует, что СКО местоопре-деления объекта убывает по мере уменьшения угла 9 о вследствие увеличения доли энергии сигнала, перехватываемой по главному лучу энергетической диаграммы направленности [5] передающей антенны. Увеличение радиусов раскрывов приемных антенн также приводит к повышению точности выполняемых измерений по линейному закону за счет возрастания парциальных КНД.

Из (12) следует, что при неизменных габаритах антенных систем точность местоопределения СШП ИРИ может быть повышена за счет применения сигналов с большим значением верхней границы полосы циклических частот, в частности высокочастотных радиоимпульсов [3; 5] c малой относительно a_T и a_R пространственной длительностью.

Таким образом, с использованием частотно-угловых характеристик плоских апертурных антенн при передаче–приеме негармонических сигналов исследована точность местоопределения излучателей последовательностей СШП-импульсов по измерениям времени их прихода в пространственно разнесенных точках. Оценены возможности ее повышения за счет выбора электрических размеров антенн и параметров сигналов.