Точные алгоритмы реализации метода наименьших модулей на основе спуска по узловым прямым
Автор: Тырсин Александр Николаевич, Азарян Алексан Артурович
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Вычислительная математика
Статья в выпуске: 4, 2017 года.
Бесплатный доступ
Описаны алгоритмы точного решения задачи оценивания параметров линейных регрессионных моделей методом наименьших модулей. Они основаны на спуске по узловым прямым. Предложенные алгоритмы включают в себя обычный спуск, спуск с использованием разреженных матриц и спуск с использованием разреженных матриц и с учетом направления спуска. Данные алгоритмы значительно выигрывают по сравнению с известным переборным алгоритмом и могут эффективно использоваться на практике. Получена оценка вычислительной сложности алгоритма спуска по узловым прямым. Приведена схема алгоритма. Методом статистических испытаний Монте - Карло был проведен сравнительный анализ предложенного алгоритма на основе спуска по узловым прямым и приближенного алгоритма Вейсфельда. Описан пример практической реализации предложенных алгоритмов.
Метод наименьших модулей, линейная регрессионная модель, алгоритм, узловая точка, узловая прямая, гиперплоскость, вычислительная сложность
Короткий адрес: https://sciup.org/14835235
IDR: 14835235 | УДК: 519.237.5:519.24 | DOI: 10.18101/2304-5728-2017-4-21-32
Текст научной статьи Точные алгоритмы реализации метода наименьших модулей на основе спуска по узловым прямым
Одной из распространенных математических моделей является линейная регрессионная зависимость. Эта модель имеет вид
У = Xa + £ (1)
г
где
X { x ij } п х т
к
a =
Г a 1 " a 2
e R m , у =
к a m У
Г y 1
У 2
x 12
x 22
X п 2
к
к Уп;
-
- заданная матрица;
G R п
х
пт /
Ле к
£ 1
к x п У
£ 2
к£ п У
G R п
-
- векторы коэффициентов
регрессии, измерений и случайных ошибок, соответственно.
Среди методов оценивания параметров модели (1) наибольшее распространение получил метод наименьших квадратов (МНК). Его использование требует выполнения ряда предпосылок, называемых условиями Гаусса-Маркова [1]. При их выполнении МНК-оценки параметров модели (1) являются состоятельными и несмещенными. Кроме того, если случайные ошибки имеют нормальный закон распределения, то МНК-оценки становятся эффективными. Однако использование МНК при нарушении условий Гаусса-Маркова может привести к значительным ошибкам при оценивании коэффициентов, а в случае присутствия в измерениях больших выбросов даже к несостоятельности оценок.
С целью обеспечения устойчивости оценок относительно отклонений случайных ошибок от гауссовой модели разработан ряд статистических методов. Данные методы основаны на более общих предположениях относительно случайных ошибок. Одним из таких методов является метод наименьших модулей (МНМ) [2]. МНМ для модели (1) имеет вид
n
Q ( a ) = Е| у- - (а , x Н min. (2)
“1 1 aeRm г=1
Несмотря на то, что, как указано в [2], МНМ появился примерно на полстолетия раньше МНК, методы решения задачи (2) разработаны в недостаточной степени. Особенно это касается проблемы получения точного определения вектора а при значительном объеме многомерных экспериментальных данных. Данная статья посвящена описанию и анализу вычислительных затрат нового подхода реализации МНМ на основе спуска по узловым прямым.
но-взвешенных квадратических приближений (называемый также алгоритмом Вейсфельда) [3-5], подход, основанный на сведении данной проблемы к задаче линейного программирования и ее приближенное решение методом внутренней точки [6], численные методы спуска нулевого порядка [7]. Недостатком этих методов в первую очередь является неточное решение, при относительной простоте целевой функции. Кроме того, не ясен вопрос качества получаемых приближенных решений.
Кусочно-линейный вид целевой функции позволяет рассчитывать на наличие быстрых и точных методов решения задачи (2). К точным методам относится сведение (2) к эквивалентной задаче линейного программирования [4, 8] и ее решение при помощи широко известного симплекс-метода и переборный алгоритм, описанный в [7].
Использование симплекс-метода ограничено задачами малой размерности. Это вызвано накоплением погрешностей из-за ошибок округлений и требованием чрезмерно большого выделения памяти.
Второй точный метод [7] основан на переборе всех узловых точек, в которых не существует производная функции Q ( а ) ни по одному из возможных направлений пространства R m . Поскольку функция Q ( а ) является выпуклой, то она имеет единственный минимум. Если минимум одновременно достигается в нескольких особых точек а 1, а 2,..., а 1 , то областью минимума будет являться выпуклое множество [9] ll
A = { а : а = ^ а k , ^ = 1}.
к=1
Введем гиперплоскости Q z = О ( а , x i , yt ) в виде уравнений
У,-(а, х> 0, (i = 1,2, K, n).(3)
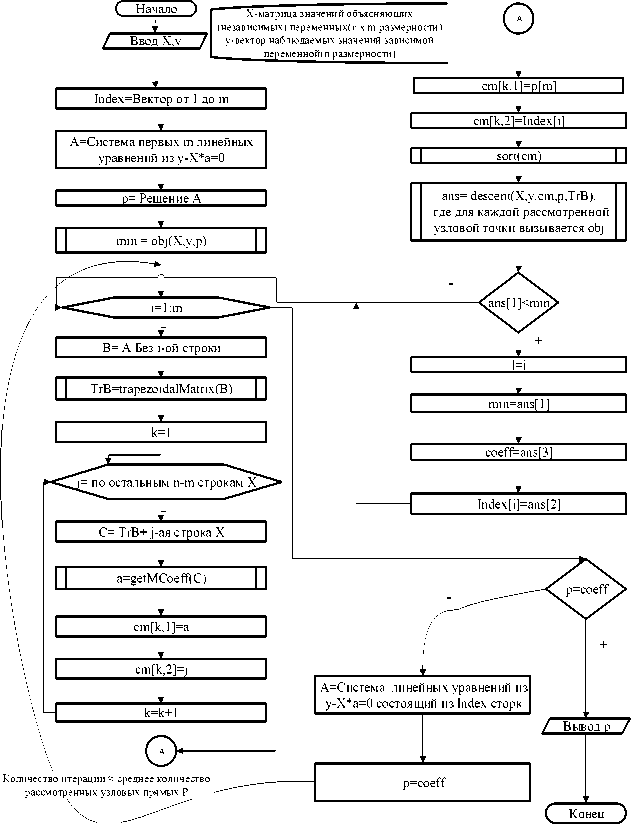
Зададим также узловые точки пересечения гиперплоскостей (3) km u (к,,..., к„) = 1 Q i , 1 ^ к 1 < k 2 I mm' i = к j Обозначим U - множество всех узловых точек (4). В [5] показано, что минимум целевой функции Q(а) принадлежит множеству U. Поэтому решение а* задачи (2) может быть получено путем перебора всех узловых точек и выбора в качестве решения той, которая обеспечивает минимум целевой функции Q(а). Переборный алгоритм требует решения Cm систем линейных уравнений порядка m. Вычислительные погрешности здесь незначительны и не накапливаются. Однако с ростом n и m наблюдается экспоненциальный рост вычислительных затрат. Фактически практическое применение переборного алгоритма ограничено объемом выборки n< 200 и числом коэффициентов регрессии m< 4 . Однако отсутствие эффекта накопления вычислительных погрешностей делает возможным использование данного метода при условии ограничения числа перебираемых узловых точек. Целью статьи является описание эффективного точного вычислитель- ного метода решения задачи (2), осуществляющего неполный перебор особых точек и его сравнительный анализ с приближенными методами. 2. Алгоритмы реализации спуска по узловым прямым Обычный спуск. Данный алгоритм точного решения задачи (2) основан на спуске к точному решению, двигаясь вдоль узловых прямых 1(k k ), каждая из которых является пересечением (m -1) различных гиперплоскостей Qi: km-1 1 (k 1,...,km-1) : IQi , 1^ k 1 < k2 <k< km-1 ^ n , ksE N . i=k1 В качестве начального приближения берется узловая точка u (k k ), являющаяся пересечением m произвольных различных гиперплоскостей Qk,...,Qk . Исключив одну из гиперплоскостей, получим узловую прямую 1 (k k ). Через любую узловую точку проходит m узловых прямых. Выберем из этих узловых прямых ту, вдоль которой целевая функция достигает наименьшего значения, которое всегда будет достигаться в одной из узловых точек. Найдя эту узловую точку, продолжим движение из нее по тому же принципу. В результате будет найдена узловая точка u*k k ) = a*, спуск из которой невозможен. Эта узловая точка будет являться точным решением задачи (2). В [10] доказано, что алгоритм спуска вдоль узловых прямых для нахождения решения задачи (2), сходится к точному решению за конечное число шагов. Поясним этот алгоритм, используя рис. 1 (для случая m = 2). В качестве начальной точки выберем точку H. Через нее проходят прямые I и II. Сначала рассмотрим прямую I. Среди узловых точек, которые лежат на этой прямой, выбираем ту, в которой достигается минимальное значение целевой функции (таким образом, происходит спуск по прямой). Предположим, что такой точкой является точка С. Рассмотрим прямую II. Спускаясь по прямой II, находим на ней точку, в которой достигается минимальное значение. Пусть, например, эта точка L. Далее, сравнивая значения целевой функции в точках C и L, выбираем ту, в которой достигается минимальное значение. Пусть, например, эта точка C. Через нее помимо прямой I проходит прямая III. На этой прямой находим очередную точку, в которой достигается минимальное значение целевой функции. Далее, сравнивая значения целевой функции в точках Си D, выбираем ту, в которой достигается минимальное значение. Пусть такой точкой является D. Допустим, что на прямой IV, проходящей через D, точкой минимума является сама точка D, тогда в качестве решения выбираем точку D, в которой достигается минимум целевой функции (если бы нашлась другая точка минимума на этой прямой, то из нее продолжили бы дальнейший спуск). Рис 1. Спуск по узловым прямым Отметим, что при вычислительные затраты данного алгоритма можно значительно сократить, если использовать информацию о предыдущей найденной узловой точке. Спуск с использованием разреженных матриц. Двигаясь вдоль прямой l(k k ), для нахождения узловых точек, принадлежащих этой прямой, нужно для каждой точки решать систему линейных алгебраических уравнений (СЛАУ) порядка m ' al + a 2 xk 1,2 + a 3 xk 1,3 + ... + amxk 1, m = Л’k1, al + a 2 xk 2,2 + a 3 xk 2,3 + ... + amxk 2, m = Ук 2, <l (5) al +a 2 xkm-1,2 +a 3 xkm-1,3 +... + ■.-1, m = ykm4> _ ai + a 2 Xi ,2 + a 3 Xi ,3 +... + amXi, m = У., где 1 < ki < k 2 <k< km4< n, i e{1,2,..., n}, г ^{ ki, k 2,к, km -1}. Очевидно, что СЛАУ двух различных узловых точек, принадлежащих этой прямой одной прямой отличаются лишь одним (последним) уравнением. Следовательно, вычислительная эффективность алгоритма спуска существенно повысится, если для нахождения узловых точек, которые лежат на прямой l(k| k _), первые (m -1) строк расширенной матрицы, соответствующей СЛАУ (5) предварительно преобразуем с помощью элементарных преобразований к ступенчатому виду. Расширенная матрица СЛУ прямой l(k ,...,k - )имеет вид ( 1 xk 1,2 xk 1,3 ■ xk1, m-1 xk1,m Уц 1 xk 2,2 xk2,3 xk2, m-1 k2 , m yk2 A (k 1,. .. km-1 = 1 xk3,2 xk3,3 xk3,m-1 xk3, m yk3 1 V x km-1 ,2 x km-1 ,3 xkm-1 ,m-1 xkm-1,m ykm-1 7 Применив алгоритм прямого хода метода Гаусса, преобразуем матрицу A (k^..,km-1) к ступенчатому виду (1 xk1,2 xk 1,3 • xk1 ,m-1 xk1 ,m ykl ' 0 1 x k 2,3 • xk2 ,m-1 x', k2 ,m yk 2 A(k1,..., km-1 - 0 0 1 xk3,m-1 xk3,m yk 3 V 0 0 0 1 xkm-1,m y ‘ km-1 7 Используя ступенчатую матрицу A(k k ) можно значительно сократить вычислительные затраты на нахождение всех узловых точек, лежащих на прямой 1(k k ). Действительно для каждой искомой узловой точки имеем расширенную матрицу ' 1 xk1,2 xk1,3 к xk1, m-1 xk1, m y^ 0 1 xk2,3 K xk2, m-1 xk2, m yk2 A (k1,..., km -1. i ) = 0 0 1 к xk3, m-1 xk3, m У k3 LL LL L L L . (6) 0 0 0 к 1 x ‘ m y ‘ km-1 ,m km-1 1 X/2 X/3к XimA Xim y, ; ,, , , Варьируя номер i в (6), найдем все узловые точки, лежащие на прямой 1 (к 1,..., km-1). Вычислительная эффективность алгоритма спуска можно повысить, если учитывать направление спуска . Спуск с использованием разреженных матриц и с учетом направления спуска. Используя ступенчатую матрицу A(k k ), и решив СЛАУ, соответствующую расширенной матрице (6), находим значение m-го коэффициента amk1,kkm-1,i), 1 < k 1 < k2 3. Анализ вычислительных затрат спуска по узловым прямым Оценим вычислительные затраты спуска с использованием разреженных матриц и с учетом направления спуска. Воспользуемся методом статистических испытаний Монте–Карло [11]. В табл. 1 для 1000 испытаний приведены средние значения общего количества рассмотренных узловых точек L и узловых прямых P (переходов с одной прямой на другую) в алгоритме спуска с использованием разреженных матриц и с учетом направления спуска для некоторых значений n и m. Случайные ошибки ε имели стандартное нормальное распределение. Таблица 1. Среднее число рассмотренных узловых точек и прямых в алгоритме спуске n Количество узловых точек L Количество узловых прямых P m=3 m=4 m=5 m=6 m=7 m=3 m=4 m=5 m=6 m=7 30 56 91 127 168 211 5,2 6,6 7,7 8,8 9,6 50 85 136 197 262 334 6,1 8,0 9,8 11,3 12,7 100 148 235 348 459 604 7,3 9,9 12,3 14,3 16,8 150 214 337 490 655 847 7,9 10,8 13,7 16,3 19,0 300 397 618 895 1205 1529 9,1 12,7 16,1 19,6 22,9 500 644 1002 1441 1905 2477 9,8 13,9 18,0 21,8 26,0 700 881 1417 2008 2665 3390 10,4 15,0 19,1 23,5 28,1 1000 1257 1946 2771 3676 4701 11,0 15,7 20,3 25,0 30,1 1500 1855 2928 4043 5413 6973 11,8 16,8 21,7 26,9 32,4 2000 2453 3867 5363 7215 9204 12,2 17,6 22,8 28,2 33,8 Оценим средние количества рассмотренных узловых точек L и узловых прямых P. Анализ полученных результатов для различных n и m показал, что L ~ O(mn) , P ~ O(mlnn) . Теорема 1. Алгоритм спуска по узловым прямым имеет вычислительную сложность W = O(m2n2+ m4n In n + m2n ln2n). Доказательство. Оценим вычислительную сложность всех основных функций, заложенных в базисе алгоритма спуска по узловым прямым. Его схема приведена на рис. 2. Рис. 2. Схема спуска по узловым прямым Функция trapezoidalMatrix расширенную матрицу размера (m -1) x (m +1) приводит к трапециевидному виду за (m -1) итерацию. В ходе i-й итерации выполняется (m + 2 - i)(2m -1 - 2i) операций умножения и вычитания. Поэтому общее количество выполненных операций I = ^(m + 2 - i)(2m -1 - 2i) = 2^(m + 2 - i)2 - 5^(m + 2 - i) = i=1 i=1 m+1 = [ j = m + 2 - i] = 2^ j2- 5^ j. j=3 „ m .2 m(m +1)(2m +1) m . m(m +1) „ Известно, что > j — —-----—------ и > j — —------ . Значит M 6 -2 Г(m +1)( m + 2)(2 m + 3) ) Г(m +1)( m + 2) I — 2 • I5 I — 5 • I3 I 6 JI 2 Функция getMCoeff к трапециевидной матрице размера (m — 1) х (m +1) добавляет строку и вычисляет m-й коэффициент. Здесь выполняется (m — 1) итераций. В ходе i-й итерации выполняется 2(m +1 — i) операций умножения и вычитания (кроме первой итерации, во время которой выполняется не 2m, а m операций умножения и вычитания). Поэтому, общее количество выполненных операций будет равно 2]—m +1 — i) + m — 1 — m2— 1 — O (m2). i—1 Функция obj функция вычисляет и возвращает значение целевой функции Q(a). Очевидно, что функция obj имеет O(mn) вычислительную сложность. Функция sort реализует сортировку полученного массива. Известно, что сортировка Хоара в среднем имеет для входного массива из n элементов O(nlnn) вычислительную сложность [12]. Функция descent, имея матрицу вида (6) и m-й коэффициент, вычисляет остальные коэффициенты и вызывает функцию obj. Данные действия выполняются циклически (количество итераций примерно равно L /(m • P) — O(mn) /(m•)(m In n)) — O(n /(m In n)). Для вычисления остальных коэффициентов выполняется (m — 1) итераций. В ходе i-й итерации выполняется 2i операций умножения и вычитания. Следовательно, общее количество выполненных операций Г Г 3 2 O< m In n • m • m3+ (n — m) • m2+ (n — m) • ln( n — m) + n • (m + mn) mlnn JJ — O (m2n2+ m4n In n + m2n ln2n + m3n) — O (m2n2+ m4n In n + m2n ln2n). Теорема доказана. Отметим, что для n > max(ln2n; m2 In n) вычислительная сложность спуска по узловым прямым W — O(m2n2). 4. Сравнительный анализ алгоритмов спуска по узловым прямым с переборным алгоритмом и алгоритмом Вейсфельда Также воспользуемся методом Монте–Карло. В каждом случае используем по 1000 испытаний. Переборный алгоритм имеет очень высокую вычислительную трудоемкость. Для иллюстрации эффективности предложенного подхода в табл. 2 указаны отношения средней продолжительности работы различных алгоритмов спуска по узловым точкам к средней продолжительности работы переборного алгоритма для количества параметров m = 5. Результаты свидетельствуют о существенном выигрыше по быстродействию алгоритмов спуска. Таблица 2 Отношение средней продолжительности работы различных алгоритмов спуска по узловым точкам к средней продолжительности работы переборного алгоритма Объем выборки n Алгоритмы спуска по узловым точкам Обычный спуск Спуск с использованием разреженных матриц Спуск с использованием разреженных матриц и с учетом направления спуска 30 111,6 138,9 284,0 100 10352,0 14725,8 42073,5 300 602404,4 911002,5 3077299,4 Сравним метод спуска по узловым прямым с приближенным алгоритмом Вейсфельда (вычислялся с точностью до 105). Результаты сравнения приведены в табл. 3. Здесь обозначено: sv(n, m) — среднее квадратическое отклонение вектора aˆ v выборочных оценок параметров модели множественной линейной регрессии относительно вектора a теоретических значений параметров для алгоритма Вейсфельда, su (n, m) — среднее квадратическое отклонение вектора aˆ u выборочных оценок параметров модели множественной линейной регрессии относительно вектора a теоретических значений параметров для алгоритма спуска по узловым прямым, tv (n, m) — среднее время вычислений для алгоритма Вейсфель-да, tu (n, m) — среднее время вычислений для алгоритма спуска по узловым прямым. Таблица 3 Результаты сравнения алгоритмов Вейсфельда и спуска по узловым прямым по точности и быстродействию n s (n, m) = sv (n, m) / su (n, m) t (n, m) = tv (n, m)/ tu (n, m) m=3 m=4 m=5 m=6 m=7 m=3 m=4 m=5 m=6 m=7 32 1,03 1,02 1,02 1,00 1,00 5,85 4,43 4,36 3,38 2,16 64 1,02 0,98 1,01 1,00 0,98 6,66 6,49 4,56 3,44 2,23 128 1,01 1,02 1,05 1,02 0,99 8,22 6,72 4,65 3,60 2,32 256 1,00 0,99 0,99 0,98 1,00 13,46 10,58 7,58 4,49 2,91 512 1,03 1,10 1,04 1,02 1,04 25,84 12,79 10,32 7,31 3,82 1024 1,02 1,04 1,04 1,00 1,08 47,66 31,06 20,11 10,83 7,61 Согласно приведенным в табл. 3 результатам при примерно одинаковой точности оценок алгоритм спуска по узловым прямым превосходит по быстродействию приближенный алгоритм Вейсфельда. Это значит, что предлагаемый точный алгоритм работает быстрее ( t(n, m) > 1 ) приближенного алгоритма Вейсфельда. Примерная близость значений отношения s(n, m) к единице означает, что алгоритм Вейсфельда стабильно сходится к точному решению с требуемой точностью. Заключение Предложены точные алгоритмы реализации метода наименьших модулей при оценивании параметров линейных регрессионных моделей, основанные на спуске по узловым прямым. Данные алгоритмы позволяют значительно снизить вычислительные затраты при точной реализации метода наименьших модулей. Выигрыш достигается за счет того, что вместо перебора узловых точек осуществляется спуск по ним. Вычислительная сложность спуска по узловым прямым позволяет на практике реализовать точное оценивание методом наименьших модулей для любых размеров экспериментальных данных. При этом, предложенный точный метод превзошел по быстродействию известный приближенный алгоритм Вейсфельда.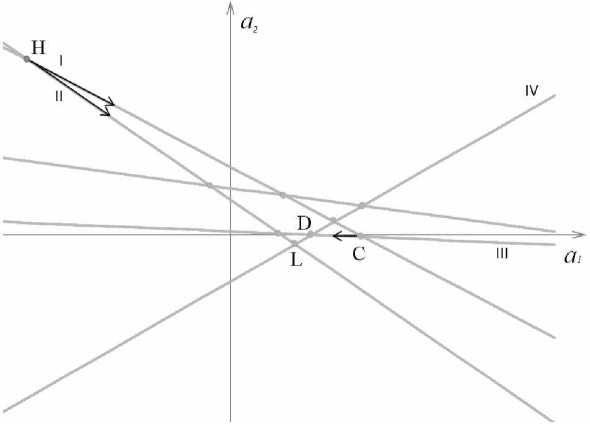
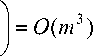
Список литературы Точные алгоритмы реализации метода наименьших модулей на основе спуска по узловым прямым
- Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Исследование зависимостей. М.: Финансы и статистика, 1985. 488 с.
- Bloomfield P., Steiger W. L. Least absolute seviations: theory, applications, and algorithms. Boston-Basel-Stuttgart: Birkhauser, 1983. 349 p.
- Weiszfeld E. On the point for which the sum of the distances to n given points is minimum//Annals of Operations Research. 2008. V. 167, № 1. P. 7-41. Translated from the French original and annotated by Frank Plastria.
- Мудров В. И., Кушко В. Л. Методы обработки измерений: квази-правдоподобные оценки. М.: Радио и связь, 1983. 304 с.
- Акимов П. А., Матасов А. И. Уровни неоптимальности алгоритма Вейсфельда в методе наименьших модулей//Автоматика и телемеханика. 2010. №2. С. 4-16.
- Boyd S., Vandenberghe L. Convex optimization. Cambridge: Cambridge University Press, 2004. 730 p.
- Тырсин A. H., Максимов K. E. Оценивание линейных регрессионных уравнений с помощью метода наименьших модулей//Заводская лаборатория. Диагностика материалов. 2012. Т. 78, № 7. С. 65-71.
- Зуховицкий С. И., Авдеева Л. И. Линейное и выпуклое программирование. 2-е изд., перераб. и доп. М.: Наука. Физматлит, 1967. 460 с.
- Рокафеллар Р. Выпуклый анализ: пер. с англ. М.: Мир, 1973. 470 с.
- Азарян А. А., Тырсин А. Н. Эффективные алгоритмы оценивания линейных регрессионных моделей на основе метода наименьших модулей//Анализ, моделирование, управление, развитие социально-экономических систем: сборник научных трудов XI Международной школы-симпозиума, Симферополь-Судак, 14-27 сентября 2017. Симферополь: ИП Корниенко А. А., 2017. С. 11-16.
- Михайлов Г. А., Войтишек А. В. Численное статистическое моделирование. Методы Монте-Карло. М.: Академия, 2006. 368 с.
- Кормен Т. X. Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ: пер. с англ. 3-є изд. М.: Вильямс, 2013. 1328 с.


