Точные решения для конформно-плоской вселенной. II. Линейное уравнение состояния и многомерные пространства-времена

При исследовании конформно-плоских пространств на основе общей теории относительности нередко получение и физический анализ соответствующих космологических моделей проводится в синхронной системе отсчета, что не всегда приемлемо с точки зрения нахождения точных аналитических решений уравнений Эйнштейна из-за ряда математических трудностей. Например, в такой системе отсчета нельзя получить в конечном виде решения для открытой космологической модели с некогерентной пылью и излучением. Однако эта задача решается с использованием несопутствующей системы отсчета ( [1]- [3]), в которой 4-метрика пространства-времени конформно-плоская, а конформный множитель зависит только от одной переменной, играющей роль расстояния в 4-пространстве Минковского (подход Фока ( [4], [5])). При этом оказывается, что такое описание эквивалентно введению кинеметрической системы отсчета (см., например, [6]- [8]) взамен синхронной [9]. Кроме того, использование синхронной системы отсчета не вполне отвечает симметрии космологической проблемы, где метрика зависит от одной переменной (см., например, [4]).

В работе [10] при обобщении фридмановской модели открытой Вселенной [11], записанной в форме Фока ( [4], [5]), получено точное аналитическое решение с произвольной функцией состояния, которая определяется как отношение давления к плотности энергии. В частных случаях функция состояния совпадает с уравнениями состояния [10], в том числе и представляющими собой линейную связь плотности энергии и давления.

В предыдущей статье [1] было найдено обобщение решения Фридмана для открытой Вселенной на случай наличия как вещества, так и равновесного светоподобного излучения (подобного электромагнитному) с отличным от нуля давлением без введения конкретного уравнения состояния. Здесь мы обратимся непосредственно к проблеме уравнения состояния вещества в космологических моделях. На наш взгляд, этой проблеме уделяется незаслуженно мало внимания, хотя уравнение состояния является неотъемлемой частью системы уравнений Эйнштейна при решении космологических задач.Тем более, что успехи инфляционного подхода при решении некоторых проблем фридмановской космологии убеждают в том, что во Вселенной могут реализовываться самые различные состояния вещества (как с положительным, так и с отрицательным давлением).

По нашему убеждению, описание эволюции Вселенной с точки зрения изменения уравнения состояния может представлять собой совершенно особый подход, естественно соединяющий в себе физический (термодинамика, кинетика) и геометрический (кривизна, размерность пространства-времени), аспекты теории эволюции Вселенной. Успехи геометрического многомерного подхода в объединении фундаментальных взаимодействий приводят к мысли, что размерность пространства-времени так или иначе должна проявляться в физических величинах, характеризующих эволюцию Вселенной.

В настоящей работе в рамках многомерного пространства-времени с одним временноподобным направлением рассматривается получение конформно-плоских моделей как точных решений космологических уравнений Эйнштейна с отличным от нуля давлением для разных уравнений состояния при наличии линейной связи между плотностью энергии и давлением. Оказывается, что такой подход приводит к выявлению некоторого дискретного набора уравнений состояния, для которых конформные множители тесно связаны с гармоническими функциями, являющимися решениями уравнений Лапласа в многомерных евклидовых пространствах целой размерности. Размерность этих пространств, в свою очередь, определяется конкретным уравнением состояния.

Мы по-прежнему будем использовать подход Фока, в котором метрика 4-мерного (и многомерного) пространства-времени конформна галилеевой, а конформный множитель является функцией одной переменной.

1.    Многомерные уравнения Эйнштейна

Поставим вопрос: к каким последствиям приведет изменение размерности пространства-времени в рамках конформно-плоских моделей и подхода Фока для уравнения состояния вещества, заполняющего Вселенную. Ответить на этот вопрос попытаемся в рамках подхода типа К ал у цы-Клейна, используя метод, который Ю.С. Владимиров [7] называет индуктивным. Другими словами, будем увеличивать число пространственноподобных координат, оставляя одну временноподобную.

Метрику запишем в виде, аналогичном тому, как это сделано в [1]:

ds2 = exp(2o) bp,vdx*dx",                                    (1.1)

где¹ exp(2o) — коіі ( 1 ) ормиып множитель ： а = o(S); S² = 8 村 x^Mx^v ； %v = diag(1 ； —1; —1;...; —1)— метрический тензор типа Минковского для многомерного пространства-времени; скорость света и гравитационная постоянная Ньютона равны единице, поэтому эйнштейновская гравитационная постоянная здесь равна к = 8n. Но теперь индексы пробегают значения 〃， v = 0,1,...,N, где N — число пространственноподобных координат.

Уравнения гравитационного поля постулируем в виде системы уравнений Эйнштейна (без космологической постоянной)

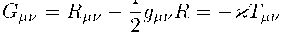
(1-2)

r 】 e Gpv, Rpv 口 R,— тетізорн Эйнштейна. Риччи ii скалярная кріівігзиа соответственно, построенные из метрики (1.1) аналогично 4-мерному случаю; правая часть - многомерный аналог тензора энергии-импульса (ТЭИ) идеальной паскалевой жидкости, описывающий многомерную «жидкость»)

T^v = fuHuv + pbpv , (I")

где¹ £ — аналог плотности 'Әпергіш ： p — aii а л or дав ле i ii ія ： (N + 1)-скор ость u * = exp(o)b^ пропорциональна градиенту переменной S как функции координат х^м : b* = S 屮 ; u^uH = 1 - условие нормировки (N + 1)-скоростіі ： b*v = u^Uv — g*v есть N-проект op na N-подпространство* который играет роль метрического тензора для N-подпространства, при этом выполняется условие ортогональности N-подпространства и времеішоподобііой конгруэнции u* : b*vu* = 0.

Фактически, если (N +1)-скорость u* определить как аналог монады в многомерном пространстве времени по аналогии 4-мерием (см., например, [7]), то можно считать, что ТЭИ (1.3) записан согласно монадному подходу .

С другой стороны, левая часть системы (1.2) может быть представлена как

^G*v = ^(N - D ( ^а" - S -^(а’⁾² bHbv - N +    s —^а’ +   2~С ) ² б*") ，      (i/)

где штрих обозначает производную d/dS.

Проводя процедуру (1 + N)-расщеплеиия как это делается в 4-мерии (см., например, [7]), получаем следующую систему уравнений , определяющих «плотность энергии» и «давление», и частным случаем которой, естественно, являются уравнения ( 国，( L4M1.5))

N(N - 1)

σ′

耳+

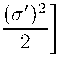
к£ exp(2o);

(1.5)

(N - 1) 卜〃 + N. ¹ / + N ₂ ² ⑺ ²] = - кр exp(2b).

(1.6)

Кавычки мы поставили потому, что, строго говоря, смысл этих понятий в случае многомерного пространства требует совершенно отдельного рассмотрения.

Как известно, открытая 4-мерная модель Фридмана [11] описывается уравнением состояния иекогереіітііой пыли р = 0, которое является частным случаем линейного уравнения состояния, во многих случаях используемого в физике,

p(S)= во • £(S),                                         (17)

где |во| < 1 ； во = const.

Ряд физически интерпретируемых состояний 4-мерии описываются соотношением р к £ : физический вакуум, некогерентная пыль, релятивистский газ и т.п., и отвечают конкретным дискретным значениям параметра во.

Уравнение состояния для многомерного пространства-времени, то есть связь между «давлением» и «плотностью энергии», постулируем в самом простом виде (1.7), который однако включает физически важные случаи.

В дальнейшем мы не будем использовать кавычки в силу того, что смысл введенных понятий плотности энергии и давления будет понятен из контекста.

Система уравнений (1.5) и (1.6) с учетом (1.7) и исключения плотности энергии £(S), сводится к одному уравнению

(，) ²

L + [(N - 1) + eoN] 下 + [(N - 2) + eoN] * = 0,               (IS)

S2

которое, в свою очередь, заменой

b ( S ) = ( N - 2) + N. o ¹ⁿ y⁽S )

для во = (2 - N)/N ii o(S) = y(S) для во = (2 - N)/N .тегко преобразуется к

У ’’ + ( N¹^^ 卜‘ = 0.                  (口。)

Хотя это уравнение интегрируется тривиально, попытаемся извлечь из него несколько иную информацию. Легко заметить, что в случае целочисленного коэффициента при первой производной уравнение (1.10) представляет собой радиальную часть сферически-симметричного уравнения Лапласа в многомерном евклидовом пространстве размерности k = N(1 + во), у’’+Y У’ = S(k-)dS (S (1噥)=0，              (LU)

где роль радиальной переменной играет все та же переменная S, величина которой сохраняется при переходах между различными евклидовыми пространствами аналогично тому, как в трехмерном пространстве радиус окружности является и радиусом сферы, построенной на этой окружности. Требование целочисленности k равносильно требованию дискретности значений во = k/N — 1, число которых для каждого фиксированного N равно (2N + 1), причем значения эти оказываются рациональными (если размерность пространства-времени является натуральным числом). При этом конформный множитель связан с функцией y(S) следующим образом:

exp(2o(S)) = у k — 2 .                                  (1.12)

Таким образом, для целых значений k решениями уравнения (1.11) оказываются фундаментальные гармонические функции порядка k (см., например, [12])

yk = ( Bk + uk-2 ) , ^k = 2 ； ^y2 = (B2 + A2 ^ln (^aS)) ,k = 2,                ( 1 」 3 )

где выбор постоянных связан с конкретной физической асимптотикой конформного множителя. При этом, строго говоря, k-мерные пространства, в которых эти функции будут гармоническими, не обязательно евклидовы, так как выполнимость уравнения (1.11) с целыми k может быть реализована и в конформно-евклидовом пространстве требованием обращения в нуль скалярной кривизны последнего. В самом деле, если рассмотреть пространство размерности n с конформноевклидовой метрикой [13]

gab = exp(2b) bab (1-14)

где¹ a, b = 1,2,… ， n; % = (+1, +1,..., +1). то скалярная кріівігзиа такого пространства ， з ашшіется в виде

^{R ( n )} =⁴ ( ПГТ )卜 ^p (-* ° )] △ "“                   ( 1.15)

где

△ пУ 三 У’’ + n-^ У’ S

Итак, в рамках нашего подхода можно констатировать, что в конформно-плоских моделях, заполненных веществом с уравнением состояния (1.7), каждому типу вещества (то есть каждому конкретному во из (физически питерпретируемого дискретного мт ю 〉 ке ст в а ， знауетшіТ] определяемому значениями N и k, соответствует «свое» евклидово (или конформно-евклидово) пространство, фундаментальная гармоническая функция которого определяет гравитационное поле (конформный множитель), создаваемое этим веществом. Тем самым в силу единственности временноподобного направления каждому типу вещества отвечает и «свое» многомерное пространство-время.

В том, что такая трактовка имеет смысл, можно убедиться, расписав закон сохранения тензора энергии-импульса для нашего случая. Проделав это, получим соотношение const р =----------—.

(1.16)

[Sexp(°)]n'

где1 n = N(1 + во) в точности совпала*?т с k. введенным ранее. Величина S exp(°(S)) = a(S) есть ни что иное, как радиус кривизны пространственноподобной гиперповерхности в синхронной системе отсчета. С другой стороны (см, например, [14])), правую часть можно интерпретировать как величину, обратно пропорциональную пространственному объему системы. Это требует, чтобы n пре,г,ставляло собой размериость последиеп.

Приведем два ярких, на наш взгляд, примера. При N = 3, во = 0 (иекогереитиая пыль) имеем n = 3. то есть плотность 'Әпергіш обратно пропорциональна трехмерному объему. При N = 3, во = 1/3 (ульту» а.у ) смяті ib 11 с т с кий газ) имеем n = 4. теперь плотность 'Әпергіш обратно пропорциональна пространственноподобному четырехмерному объему. Другими словами, состояние вещества определяет «характерное» для данного вещества пространство, в котором плотность энергии убывает обратно пропорционально объему. Более того, легко увидеть, что единственным состоянием, для которого плотность энергии будет конечной на конусе S = 0, является физический вакуум (во = — 1) - независимо от размерности N.

2.    Четырехмерное пространство-время

Теперь мы конкретизируем значение размерности N. Так как нас прежде всего интересует многообразие, описывающее нашу Вселенную, то положим N = 3 и рассмотрим, какие значения во будут характерны для второ случая (в смысле нашей трактовки).

Размерность лапласиана, то есть евклидова (конформно-евклидова) характерного пространства будет в этом случае определяться по формуле n = 3(1 + во)

(2.1)

Дискретный набор значений во, обеспечивающий целочисленность размерности (фундаментальность гармонических функций), будет содержать семь значений, начиная с нуля (напомним, что мы ограничились условием | во | 工 1). Иначе говоря, конформно-плоскому 4-миру при различных во- связанных с полыми n. соответствует семь (n = 0,1,…'6) съкліідовых (кон ( ] ) ормтю-евклидовых) пространств.

Выпишем для всех значений n (0 < n < 6) конформные множители, давление, четырехмерные и трехмерные скалярные кривизны, собственное время как функцию переменной S и метрику в синхронной системе отсчета.

• 2.1.    n = 0, во = —1

Состояние материи: физический вакуум (открытое решение де Ситтера)

Конформный множитель:

exp(2o) = ( B + AS2) 2 ,

⑵ 2)

где¹ A ii B - постоянные. Очевидно, что ве ： з,г,е можно положить B = 1. так как в та константа определяет выбор масштаба.

Зная конформный множитель, легко находим давление как функцию переменной S:

кр = 3в

2S" + ⑺ ² 卜 Xp^(-2G ・

(2.3)

Проделав несложные вычисления, получим ожидаемый результат: давление постоянно и зависит только от констант

к р = 12A,

(2-4)

откуда видно, что постоянная A отрицательна (плотность энергии должна быть положительной). Четырехмерную скалярную кривизну находим по формуле

⁴R = 6exp(-2 。)卜" + ^|- + (o')²] = —48A > 0.

⑵ 5)

Трехмерная скалярная кривизна в случае с метрикой (1.1) в несопуствующей системе отсчета вычисляется с помощью 3-проектора bik = UiUk — gik (ui = e-"bi - 4-скорость; bi = S," и равна

зз     3 。 '

R = —~ exp(—2 。 ).

S

(2.6)

Для физического вакуума эта кривизна принимает вид

3R = 6A (1 + AS2).

(2.7)

При S т 0 3 R стремится к конечному пределу (6A).

Преобразованием t = S cosh R, r = S sinh R решение с метрикой (1.1) переводится в сопутствующую синхронную систему отсчета, где собственное время определяется как

τ

uµdxµ

/ exp[o(S)]dS,

⑵ 8)

з,г,есь uM - 4-скорость, которая в обш.ем случае не выражается в 'Элементарных (функциях (j)to. по всей видимости, и обуславливает «нежелание» многих работать с конформно-плоскими метриками. Интервал записывается как dS2 = dT2 — а2(т) (dR2 + sinh2 RdQ2),

⑵ 9)

где¹ а(т) = e"S - масштабный ( ] ) актор.

В нашем случае собственное время легко находится и равно

τ

ln

1 + Тй$

1- 7|A|S

^= arctan h( ， |A|S).

⑵ 10)

Выбирая область изменения тот 0 до х, получим область изменения S : 0 < S < (1/ ， |A|).

Соответствующую скалярную 3-кривизну в сопуствующей синхронной системе отсчета получаем в виде

(2.11)

а интервал записывается в стандартной форме dS 2

dT2 - i"

sinh² (2 ， | A | t )dl².

(2.12)

• 2.2.    n = 1, во = - 2/3

Состояние материи: доменные стенки. Конформный множитель:

ехр(2о) = (1+ AS )^-4 .

Давление:

Kp = 8A ( 1 + AS² ) ;

S

⑵ 13)

⑵ 14)

при ' ；) том A < 0.

Четырехмерная скалярная кривизна:

⁴R = -图 A ( 1 + AS² ) ² .

⑵ 15)

Трехмерная скалярная кривизна в несопуствующей системе отсчета:

³R=(6AI ( 1 + AS ) ³.

⑵ 16)

Собственное время:

т = ( | A | (1 + AS))^-1.

(2.17)

Метрический элемент в синхронной системе отсчета:

dS² = dT² - A ² t ⁴dl².

(2.18)

• 2.3.    n = 2, во = - 1/3

Состояние материи: релятивистские струны. Конформный множитель:

ехр(2а) = S 2A.

(2.19)

Давление:

Kp = - A (A + 2) S^-2(A+1).

(2.20)

Четырехмерная скалярная кривизна:

4R = 6A( ： + ： )

Трехмерная скалярная кривизна в несопуствующей системе отсчета:

(2.21)

3R

3A

S2( A +1)'

(2.22)

Собственное время:

т —     ¹ Q ( A +1 )

(2.23)

T =(A +1) S ■

Метрический элемент в синхронной системе отсчета:

dS² = dT² - [ (A + 1)т] \A + ¹ 丿 dl².

(2.24)

Необходимо отметить, что этот случай является особым как с точки зрения гармонических функций, так и с точки зрения физического содержания получаемой модели: в зависимости от знака и величины постоянной A можно получать как сингулярные, так и несингулярные модели.

2.J. n = 3, во = 0

Состояние материи: некогерентная пыль (Вселенная Фридмана). Конформный множитель:

exp(2o)

(1+ 》

(2.25)

Давление и плотность энергии:

p = 0 ； К£

12A

S3 (1 + A/S)6

(2.26)

откуда видно, что постоянная A отрицательна. Четырехмерная скалярная кривизна:

4R

12A

S3 (1 + A/S)6

(2.27)

Трехмерная скалярная кривизна в несопуствующей системе отсчета:

Собственное время:

3R

6A

S³ (1 + A/S )5

(2.28)

^T = S - ^2Aln|S| — A.

AS

(2.29)

Масштабный множитель в синхронной системе отсчета не выражается непосредственно через собственное время, как и в стандартном подходе (см, например, [14]).

2.5. n = 4, во = +1/3

Состояние материи: ультрарелятивистский газ. Конформный множитель:

exp(2o) = ( 1 + A/S 2 ) 2.

(2.30)

Давление:

A

S⁴ ( 1 + A/S 2 ) 4

(2.31)

Четырехмериая скалярная кривизна 4R = 0, что с очевидностью следует из равенства нулю следа тензора энергии-импульса в этом случае.

Трехмерная скалярная кривизна в несопуствующей системе отсчета:

3R

6A

S4(1 + A/S2)3

(2.32)

Собственное время:

t = S +

?^-5 + 嘉).

(2.33)

Метрический элемент в синхронной системе отсчета:

dS² = dT² — Т----- dl²; T = т +

〜        4 | A |

τ- v/7—

(2.34)

из которого видно, что выбор знака перед корнем и значения постоянной будут определяться граничными условиями в конкретной модели, но при больших временах a² 〜 т.

2.6. n = 5, во = +2/3

Состояние материи: нерелятивистский вырожденный газ. Конформный множитель:

exp(2o) = ( 1 + A/S в ) ⁴/³.

(2.35)

Давление:

κp

8A

S⁵ ( 1 + A/S з ) ^10/3'

(2.36)

Четырехмерная скалярная кривизна:

4R

12A

S5 ( 1 + A/Sз ) ^10/3 .

(2.37)

Трехмерная скалярная кривизна в несопуствующей системе отсчета:

3 R

6A

S5 ( 1 + A/S³ ) ^7/3 .

(2.38)

Собственное время как функция от S не выражается в элементарных функциях.

• 2.7.    n = 6, во = +1

Состояние материи: сверхжесткое состояние. Конформный множитель:

exp(2o) = ( 1 + A/S 4 ) .

Давление:

12A

S⁶ ( 1 + A/S 4 ) 3

(2.39)

(2.40)

Четырехмерная скалярная кривизна:

4R

24A

S 6 ( 1 + A/S 4 ) 3

(2.41)

Трехмерная скалярная кривизна в несопуствующей системе отсчета:

3R=——6A—.

(2.42)

S6 (1 + A/S 4)2

Итак, в случае четырехмерного пространства-времени мы имеем семь физически интерпретируемых значений во (уравнений состояния материи, заполняющей пространство-время), допускающих описание создаваемых гравитационных полей (конформных множителей 4-метрики) на языке фундаментальных гармонических функций соответствующих евклидовых пространств. Основные полученные выше данные для четырехмерного пространства-времени для сравнения сведены в Табл.1.

Таблица 1

n	n - 1	β0	Состояние материи	exp ( 2 o( S ))
0	-1	-1	Физический вакуум	(B + A • S2)-2
1	0	-2/3	Доменные стенки	(b + A • S)-4
2	1	-1/3	Релятивистские струны	A • S2B
3	2	0	Некогерентная пыль	(B + A/S)4
4	3	+ 1/3	Релятивистский газ	(B + A/S 2)2
5	4	+2/3	Нерелятивистский вырожденный газ	(b + A/S 3)4/3
6	5	+1	Сверхжесткое	(B + A/S4)

3.    Таблица состояний материи в многомерном пространстве-времени

Теперь мы вновь обратимся к соотношению, связывающему во из уравнения состояния, размерность «опорного» пространства-времени (N +1) и размерность фундаментальной гармонической (функции n. Так как в «опорном» многообразші нам ік?обходіімо 口 меть хотя бы одно времешюпо-добное направление и одно пространственноподобное (чтобы понятие пространства-времени имело смысл), то естественно начать рассмотрение моделей с N = 1. Напомним, что для каждого фикси-ров ашюго N чіі сто ассотцшров аппых евклидовых (кон 巾 ор мио-ев клиповых) простраиств. то есть фундаментальных гармонических функций, ограничено и равно (2N + 1).

Полная картина наглядно отражается в виде Табл.2, в которой по горизонтали отложены значения N. а по вертикали - размерность ассотцшров ашюго евклидов а ( koi i ( J ) op м i ю- ев к л іідов а) пространств a n. От метим иекоторые в ажные. на іі аш в взгляд, мо менты. ха ， р актериые для вт оіі т аблішы.

Таблица 2

N/n	1	2	3	4	5	6	7	8	9	10	11
0	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1
1	0	-1/2	-2/3	-3/4	-4/5	-5/6	-6/7	-7/8	-8/9	-9/10	-10/11
2	+1	0	-1/3	-2/4	-3/5	-4/6	-5/7	-6/8	-7/9	-8/10	-9/11
3		+ 1/2	0	-1/4	-2/5	-3/6	-4/7	-5/8	-6/9	-7/10	-8/11
4		+1	+ 1/3	0	-1/5	-2/6	-3/7	-4/8	-5/9	-6/10	-7/11
5			+2/3	+ 1/4	0	-1/6	-2/7	-3/8	-4/9	-5/10	-6/11
6			+1	+2/4	+ 1/5	0	-1/7	-2/8	-3/9	-4/10	-5/11
7				+3/4	+2/5	+1/6	0	-1/8	-2/9	-3/10	-4/11
8				+1	+3/5	+2/6	+ 1/7	0	-1/9	-2/10	-3/11
9					+4/5	+3/6	+2/7	1/8	0	-1/10	-2/11
10					+1	+4/6	+3/7	-2/8	+ 1/9	0	-1/11
11						-5/6	+4/7	-3/8	-2/9	+ 1/10	0

Легко видеть, что только три «состояния» присутствуют во всех размерностях пространства-времени: «физический вакумм», «пыль» и «сверхжесткое состояние». Они взяты в кавычки ввиду того, что физическая интерпретация конкретных значений в различных размерностях требует отдельного рассмотрения. В связи с этим показателен тот факт, что в четырехмерном мире (третий столбец) все «возможные» значения в имеют ясную физическую трактовку и включают в себя все основные состояния вещества, используемые для нахождения космологических решений.

Необходимо указать на то, что гармонические функции одного и того же порядка (другими словами, один и тот же конформный множитель) отвечают различным зиечепиям во в разных размерностях. Тогда на таком языке можно говорить о некотором «унифицировании» типов взаимодействий, так как для любого во (кроме физического вакуума, что также весьма примечательно) найдется такое пространство-время, в котором соответствующий конформный множитель будет описывать модель, заполненную веществом типа пыли с во = 0.

К интересному заключению можно прийти, обращаясь опять к 4-мерному пространству-времени: переход к 5-мерию «унифицирует» электромагнитное взаимодействие (что, кстати, вполне соответствует подходу Калуцы-Клейна); переход к 6-мерию «унифицирует» состояние ве-тті ( ?ств ас во = +2/3- которое спр аведлпво для всех идеальных систем ： больим ановскпх. боз оппых ii фермионных (см, например, [15]). То есть речь идет об электрослабом взаимодействии. Введение

7-мерия «превращает в пыль» вещество со свержестким уравнением состояния в 4-мерии, иначе говоря, когда в 4-мерии реализуется сильное взаимодействие. Это согласуется с результатами Ю.С. Владимирова [16], который показал, что в рамках подхода Калу цы-Клейна для объединения гравитационного и электрослабого взаимодействия достаточно 6-мерного пространства-времени, а для объединения грави-электро-сильных взаимодействий - 7-мерного пространства-времени с одним временноподобным направлением.

С другой стороны, одному и тому же значению во могут соответствовать различные порядки фундаментальных гармонических функций, то есть различные конформные множители в зависимости от размерности простраиства-времии. Так во = +1/3 описывается гармонической функцией четвертого порядка в 4-мерии, гармонической функцией восьмого порядка в 7-мерии, двенадцатого порядка в 10-мерии и так далее. Конечно, нужно помнить о том, что конкретное значение во отвечает различным физическим условиям в различных (в смысле размерности) мирах.

Существенным моментом такого подхода является, на наш взгляд, возможность описания моделей конформно-плоской Вселенной, заполненной веществом с произвольным во.

4.    Заключение

В настоящей работе в рамках многомерного пространства-времени с одним временноподобным направлением рассмотрено получение конформно-плоских космологических моделей как точных решений уравнений тяготения для разных уравнений состояния с линейной связью между давлением и плотностью энергии. При этом тензор энергии-импульса взят как обобщение ТЭИ в приближении идеальной паскалевой жидкости в четырехмерии. Частным случаем такого ТЭИ является ТЭИ некогерентной пыли с нулевым давлением, связанный с открытой моделью Вселенной Фридмана. Оказывается, что введение такого уравнения состояния приводит к выявлению некоторого дискретного физически интерпретируемого набора уравнений состояния, для которых конформные множители тесно связаны с гармоническими функциями, являющимися решениями уравнений Лапласа в многомерных евклидовых пространствах целой размерности. Размерность этих пространств, в свою очередь, определяется конкретным уравнением состояния материи.

Для четырехмерных пространств-времен приведена соответствующая таблица, позволяющая проследить связь между дискретным набором линейных уравнений состояния, размерностью вспомогательного евклидового пространства и функциональным видом конформных множителей открытых космологических моделей, связанных с гармоническими функциями, удовлетворяющих уравнениям Лапласа в этих вспомогательных евклидовых пространствах. При этом видно, что пространственное трехмерие ограничивает выбор дискретных физически интерпретируемых уравнений состояния для получения точных решений уравнений тяготения, связанных с гармоническими функциями. Поэтому, с одной стороны, с заданной наперед точностью можно любой рациональной дробью апроксимировать любое линейное уравнение состояния, а, с другой, только расширив пространство-время до необходимой размерности, можно записать точное решение многомерных уравнений Эйнштейна, связав его с гармоническими функциями.

При увеличении пространственной размерности N (N > 3) такая возможность появляется для любого линейного уравнения состояния с рациональным коэффициентом пропорциональности. Для таких пространств-времен приведена аналогичная таблица, но без фиксации размерности пространственной гиперповерхности. При этом каждому значению пространственной размерности N отвечатот 2N + 1 липе иных уравпенни состояний. 9та табггшв’ демонстрирует во ： зможпости для каждого такого уравнения состояния с рациональным коэффициентом пропорциональности между давлением и плотностью энергии при построении любой открытой космологической модели с конформно-плоской метрикой, но в соответствующем пространстве времени с размерностью больше четырех.