Точные решения для конформно-плоской вселенной. IV. Космологическая модель для «бутылочного» потенциала

Новый метод получения точных решений космологических уравнений Эйнштейна с помощью эквивалентных потенциалов был предложен в работе [1] и продемонстрирован при нахождении обобщений решения Фридмана, для описания открытой Вселенной, заполненной идеальной жидкостью с переменным уравнением состояния (или функцией состояния, введенной в [2]). При этом был использован подход Фока ( [3]- [4]) для записи метрики 4-мерного пространства-времени в конформно-галилеевой форме, ds2 = exp(2a)5^V dx^dx17, (0.1)

с конформным множителем exp(2a) как функции од ной переменной S , квадрат которой представляет собой произведение запаздывающего и опережающего времен в трехмерном мире: S ² = 6^_Vx^x^v = t² — r² = (t — r)(t + r) = uv; 1 1 a = a(S ) i1 §^_V = diag(1; — 1; — 1; — 1) - метрический тензор Минковского; ц, v = 0,1, 2, 3; скорость света и гравитационная постоянная Ньютона равны единице, поэтому эйнштейновская гравитационная постоянная здесь равна к = 8п.

В дальнейших работах [5] и [6] развивается данный подход для классических уравнений Эйнштейна. с правой частью (без космологической постоянной), выбранной в виде тензора, энергии-импульса (ТЭИ) в приближении идеальной жидкости,

^T^ £u^uv ⁺ pb^V , (0-2)

где е - плотность энергии; р - давление; 4-скорость u^ = exp(o')b^ пропорциональна градиенту переменной S как функции координат x^M : b^ = S,^ ; u^u^ = 1 - условие нормировки 4-скорости; b^_V = u^u_V — g^_V есть 3-проектор на 3-пространство, который играет роль метрического тензора для 3-пространства, при этом выполняется условие ортогональности 3-пространства и временноподобной конгруэнции u^M : b^_Vu^ = 0.

В результате (1+3)-расщепления (см., например, ( [7]- [8])) система гравитационных уравнений с метрикой (0.1) сведется к системе двух дифференциальных уравнений в полных производных:

3 (2 S + (a')2)

= ке • exp(2a);

(0.3)

Г и 2a '

2 V + ~ +

С)=

—кр • exp(2a),

(0.4)

где штрих обозначает производную d/dS.

Эта система (0.3-0.4) заменой о = 2 • ln(y) может быть сведена к более простой (см. [1])

• ¹² • y' yy' + s¹ • y^ = ^Ke • y⁶;

  (0.5)

  
  

  ⁴ • (^y"⁺ Syo = -

  
  

  κp · y⁵.

  
  

  (0.6)

  
  

Как уже упоминалось в [6] уравнение (0.6), содержащем давление, с помощью замен:

y = Z 1 (1/S)    либо     y = Z 2 (S)/S,                           (0.7)

можно свести к уравнению d2z/dx2 = F (x,z,p),                                    (0.8)

где переменная x в первом случае равна, x = 1/S, а. во втором - x = S.

Уравнение (0.8) аналогично уравнению Ньютона в классической механике для частицы с единичной массой, если F (x,z,p) интерпретировать как некоторую силу (в дальнейшем потенциальную. F = —dU/dz. см. ( [1]- [G]) Y При этом z - одна, из функций z 1 , z ₂ .

В [1] уже была упомянута соответствующая аналогию с внешней и внутренней задачами в теории потенциала, где внешнее решение (решение уравнения Лапласа) зачастую ищется в первом виде, а внутреннее решение (решение уравнения Пуассона) - во втором виде. В частности, в работе [1] была рассмотрена возможность первой замены, приводящей к точному космологическому решению, описывающее субстанцию, которая при больших временах ( S ^ то) распадается на некогеретную пыль (с p = 0) и равновесное светоподобное излучение (с prad = (1/3) erad), и асимтотически переходит в решение Фридмана, в форме Фока [3]: exp(2o_F ) = (1 — AF /S)⁴, где AF есть постоянная из решения Фридмана.

1.    «Бутылочный» потенциал

Следующим шагом после работ [1], [5] и [6] является выбор потенциала, четвертой степени по z,

U = (A²/4)(z² — а²)² ,                                     (1.1)

где Айа- некоторые постоянные.

Иллюстрация поведения такого потенциала приведена па Рис.1.

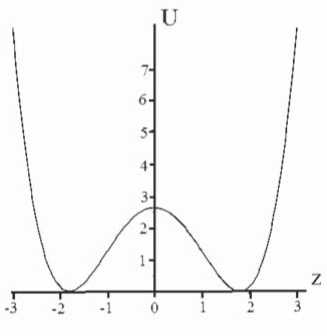
Рис. 1. Пример поведение функции «бутылочного» потенциала U для частных значений параметров А = 1 11 а = 1, 8.

Воспользовавшись законом сохранения «энергии» для соответствующей механической системы с потенциальной силой F = —dU/dz и массой m = 1, получим соотношение

1 / dz А

2 (dsy

+ U (z ) = E,

(1.2)

где E- постоянная, являющаяся аналогом полной энергии.

Вводя далее безразмерную переменную x = yS и используя (1.1), можно свести уравнение (1.2)

к квадратуре

/

γ

^у(А²/2) • (—z⁴ + 2z ²а² — а⁴ + (4/A²)E)

dz = x — xo,

(1.3)

которая после нахождения корней полинома четвертой степени в зависимости от выбора условия положительности корней может быть представлена в виде:

() /^ / ,    1     dz) = x — x

\AVa2 + b2                      (a2 — z2) • (z2 + b2)   / где a2 = (2/A)VE + a2. b2 = (2/A)VE + а2. При этом a2 + b2 = (4/A)VE; a2 • b2 = (4/A2)E — а4.

Решение уравнения (1.4) относится классу эллиптических функций Якоби (см., например, [9]). Воспользовавшись результатом [10] (с.410, формула (17.4.51)) по нахождению функции z из (1.3), при выборе xo = 0 получим решение в виде

^Va^Tb2   a2

(1.5)

z(€) = Д  ab  'ЛТД)

где sd(Z, m) - одна, ыз фуиций Якоби, связанна.я с другими функциями Якоби как sd(Z, m = sn(Z, m)/dn(Z, m); m _ модуль функции Якоби, который здесь равен m=

a

a2 + b2

1 Л   а2 А А

2 ^ \+2VE/

(1.6)

а. переменная €

€ =

a2 + x, .

(1.7)

поэтому

Z = € Va² + b² ab

A(a2 + b2)

x

V2Yab

A(4E)1/4

V1 — TE

x=

λa

V2 • m b

x=

λ

V2 • m

Д+7

V 1 — У

• x = n • x,

(1.8)

α2λ где У = ——.

2 VE Таким образом,

z(x) = sd(nx, m).

(1.9)

Функция y(x) = yz ( x ) /x, связанная с конформным множителем как y(x)² = exp(2a), в этом случае запишется в виде

, .    Ysd(nx,m).

y(x)= ^{Y ( n} ' )                                            (1.10)

x и в точке x = 0 равна, постояшюй y(0) = 7ц. Если выбрать y(0) = 1, то y = 1/n, 410 означает отсутствие сингулярности в начальный момент возникновения Вселенной.

2. Функция состояния

Аналогично как и в предыдущих работах ( [1]- [6]) введем функцию состояния,

e(x) = Р^

(2.1)

которая в каждой фиксированной точке x есть уравнение состояния.

В пашем случае давление и плотность энергии соответственно равны

Kp(x) = —4

γ3 xy(x)5

d2z(x) dx2 ;

(2.2)

k e ( x ) = 12

γ4 x2y(x)6

dz (x) dx

dz(x) dx

^z(x) \ x^.

(2.3)

В итоге функция состояния запишется как

в(х)

z (x) •

d2z(x)

dx2

dz(x) dx

dz(x)

dx

zMA

x

(2.4)

или после подстановки решения (1.9) получаем

^в(х) = -3 n^x f

Пх • sn 2 (nx, m) • (m²sn²(nx, m) - 2m² + 1)

Пх • sn 2 (nx, m) + sn(nx, m) • cn(nx, m) • dn(nx, m) - nx

В продело x ^ 0 приходим к уравноншо состояния физического вакуума, в = -1, 10 есть решение стремится к решению де Ситтера, запись которого в используемых в данной работе обозначениях приведена в [11].

Если в качестве иллюстрации взять n = 1 и m = 0.85, то получим поведение функции состояния в(х) вблизи «начала» Вселенной, изображенное на Рис.2.

Такое поведение означает, что может быть реализована инфляционная модель Вселенной без введения дополнительного скалярного поля, введенное эквивалентное уравнение Ньютона для «бутылочного» потенциала, может рассматриваться как уравнение некоторого эквивалентного скалярного поля z (переменная S включает в себя зависимость от всех четырех координат x^V

.

(2.5)

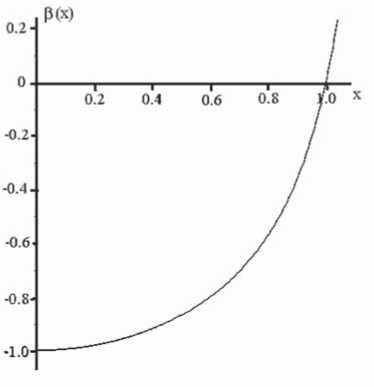
Рис. 2. Поведение функции состояния в(х) Д^ля «бутылочного» потенциала со значениями параметров П = 1 11 m = 0.85.