Точные решения в нелинейной модели теплопередачи

Рассмотрим нелинейное параболическое уравнение второго порядка

U t = Ф(и ) xx + MU ),                             (1)

которое является весьма известным и популярным математическим объектом, поскольку обладает как интересными математическими свойствами, так и многочисленными приложениями. В физике и математическом моделировании (1) применяется (в различных формах) для описания процессов, протекающих в высокотемпературной плазме [1], фильтрации жидкостей и газов в пористых средах [2], популяционной динамики [3] и т.п. Математические свойства (1) исследуются в (без преувеличения) тысячах публикаций. Особого упоминания, по мнению авторов, заслуживают работы российских (советских) ученых: А.А. Самарского (с соавторами) [4], О.А. Ладыженской (с соавторами) [5] и фундаментальная монография испанского автора Х.Л. Васкеса [6].

Одной из интересных математических особенностей (1), которая, отметим, тесно связана с приложениями, является то, что в случае, когда Ф(0) = Ф(0) = 0, у него появляется один специфический класс решений. Последние, будучи, вообще говоря, нетривиальными и неотрицательными, обращаются в нуль на некотором многообразии: U|a(t,x)=o = 0. Такого рода решения иногда именуют тепловыми волнами [1] или волнами фильтрации [7]. По-видимому, впервые они были обнаружены в 40-е годы прошлого столетия в связи с исследованиями процессов, происходящих после ядер-ного взрыва [8]. Несколько позднее подобные математические объекты были использованы для моделирования фильтрации газа в пористой среде [9]. Большое внимание таким решениям уделяется в научной школе А.Ф. Сидорова [7], в качестве инструмента исследования обычно применяется метод специальных рядов [10]. Среди работ, посвященных решениям упомянутого вида, особое место занимают работы С.Н. Антонцева с соавторами (см., например, [11]), в которых (1) рассматривается с весьма общих позиций.

В литературе наиболее распространен случай степенных нелинейностей – когда Ф(и) и Ф(и) представляют собой степенные функции. Именно он является основным объектом рассмотрения в упомянутых выше классических работах [4, 6, 7]. Одним из ключевых направлений развития теории уравнений математической физики можно назвать построение и изучение точных решений [12]. В связи с точными решениями уравнения (1) со степенными нелинейностями могут быть упомянуты работы представителей научной школы А.А. Самарского [13], а также иркутских математиков [14].

1.    Постановка задачи

Уравнение (1) в случае степенных нелинейностей с помощью простой замены (см., например, [15]) легко преобразуется к виду ut = uuxx +—uX + aue. (2) σx

Будем предполагать, что уравнение фронта тепловой волны может быть разрешено относительно x и тогда условие на ее фронте следующее:

^{u ( t}, ^{x )} | x=a(t) °' ⁽³⁾

Для задачи (2), (3) при β ∈ N выполняются условия доказанной авторами ранее теоремы [15], которая обеспечивает существование и единственность нетривиального аналитического решения, меняющего знак при переходе через линию x = a(t). Неотрицательная часть указанного решения вкупе с тривиальным и = 0 (его существование при в >  ° очевидно) образует уже упоминавшуюся тепловую волну, распространяющуюся по нулевому фону с конечной скоростью a'(t) < то.

Поскольку доказательство теоремы носит конструктивный характер и содержит рекуррентную процедуру построения решения в виде характеристического [16] ряда, его, в принципе, можно использовать для верификации результатов численных расчетов. Так, авторы имеют подобный опыт проверки с использованием отрезков рядов вычислений, выполненных с помощью алгоритмов на основе метода граничных элементов (МГЭ) [17,18] и разностной схемы [19]. Однако при нецелых значениях в > ° теорема, вообще говоря, неприменима, кроме того, радиус сходимости характеристического ряда, как правило, неизвестен и невелик. В этом контексте дополнительную актуальность приобретает проблема построения точных [12] решений, имеющих тип тепловой волны.

Ранее авторами данная проблематика рассматривалась как в частном случае а = 0 [20,21], так для уравнения (2) общего вида [15,22]. Были получены точные обобщенно-автомодельные решения и = u1(t)u2(x/a(t)) и решения в виде обобщенной бегущей волны и = u1(t)u2(x — a(t)). Они строятся в виде степенных рядов, для которых в некоторых случаях найдены оценки радиусов сходимости [20]. Выполнен анализ свойств решений методами качественной теории [23] обыкновенных дифференциальных уравнений (ОДУ) [21, 22].

В ходе исследований, проведенных в упомянутых выше работах авторов, остались некоторые открытые вопросы, представляющие интерес для области исследования. В частности, случай нецелых положительных значений β был разобран [24] не полностью даже для решений типа простой волны. Кроме того, напрашивается рассмотрение иных способов разделения переменных, например, когда функция u 1 = u 1 (x), т.е. зависит не от t, как в опубликованных статьях, а от x. В рамках настоящей работы авторами получены результаты, позволяющие продвинуться в решении данных вопросов. В частности, для двух динамических систем, к которым сводится нахождение точных решений типа тепловой волны для (2), получены фазовые портреты, что позволило установить некоторые свойства решений. Кроме того, построены разложения последних в степенные ряды, анализ коэффициентов которых дал возможность оценить радиусы сходимости, а также сделать другие содержательные выводы.

2.    Редукция к обыкновенным дифференциальным уравнениям

Вначале рассмотрим решения, имеющие тип бегущей волны. Пусть u = v(x — ^t).

Подстановка данного выражения в (2) приводит к следующему ОДУ:

vv" + -—-—+ ^v' + av ^e = 0.                         (4)

σ

К уравнению (4) добавляем условия Коши

v(0) = 0, v ' (0) = — ца.                                (5)

Первое из условий (5) является следствием (3), а второе обеспечивает совместность уравнения и существование нетривиального решения. Задача Коши (4), (5) будет предметом изучения в последующих разделах.

Также будем искать точное обобщенно-автомодельное решение (2), (3) в виде

u(t,x) = ф(x)v(z), z = x/a(t).

Отметим, что данный способ получения решений искомого типа ранее нами не рассматривался. В результате постановки получим уравнение ф2(х) „    ф2(х) , 2    (     1\ 2ф(х)ф'(х)        Г(ф'(х))2                1 2

^{vv +}             ■¹-)             ^{vv +          + ф ( х ) ф ( x )}] ^v 2 ⁺

+ *)“'№ v + аф» (x)v» = 0.                     (6)

a ² ( t )

Далее сделаем в (6) замену независимой переменной s = ln z, в результате которой уравнение примет вид ф2(х) 7 И           ф2(х) , ,х2 о (Л 1А ф(х)ф'(х) , Г(ф'(х))2         х J 2

-^x^ v(v " — v ' ) + -^122(v ' ) 2 + 2 м + - J -^x-^vv ' +     _а   + Ф(х)Ф ‘‘ (х) v ² +

+ x     a (t) v' + афв (x)ve = 0.(7)

a(t)

После приведения подобных и умножения обеих частей на х2/ф2(х) получим vv'' + 1(v')2 + [2 fl + 1) x^ — 11 vv + -x^ [(^W- + ф"(x)1 v2+ a                 -/ Ф(х)             Ф(х)-

+a/tf “x\v' + ax2фв-2(x)vв = 0.(8)

a(t) ф(х)

Предложение 1. Уравнение (8) является ОДУ тогда и только тогда, когда 1) а = 0 или а = 0, в = 1; 2) Ф = Ax ² ; 3) a(t) = exp(Bt) или a(t)=B, где A = 0 и B = 0 -произвольные константы.

Доказательство. Обоснование справедливости предложения состоит в последовательном рассмотрении всех коэффициентов в уравнении (8). При этом ф(х) определяется из алгебраического уравнения ф(х)/х ² = A, а a(t) - из дифференциального a ' (a)/a(t) = B . □

Далее будем рассматривать случай, когда a(t) = exp(Bt). В условиях предложения 1 уравнение (8) имеет вид

1            4            4\ B а vv +— (v')2 + ( 3 +— j vv + f 2 +— j v2 + Av' + Av = 0.

Пусть A = B > 0, а > 0. Тогда (9) несколько упрощается vv" + -1 (v')2 + (3 + -^ vv' + (2 + -^ v2 + v' + B-v = 0.

Для уравнения (10) рассматриваются условия Коши (5): первое из условий по-прежнему следует из (3), а второе обеспечивает совместность уравнения и существование нетривиального решения. Решение задачи (10), (5) (его существование и единственность следуют из ранее доказанной теоремы [15]) дает решение задачи (2), (3) вида u = Bx2v(s), s = In z = Inx — Bt.

При этом u| _x=_exp(Bt) = 0 приводит к v(0) = 0; при x ^ +0 имеем, что s ^ —то, т.е. решения задачи (10), (5) представляют для нас интерес на (—то, 0].

3.    Качественный анализ

Для получения свойств решений задач (4), (5) и (10), (5) выполним их анализ методами качественной теории обыкновенных дифференциальных уравнений [23]. Рассмотрим обе задачи последовательно.

Вначале перейдем от уравнения (4) к динамической системе. Для этого предварительно сделаем замену независимой переменной и искомой функции. Пусть v'(h) = Р, h = ve.

Тогда уравнение (4) запишется как fihpd- + p" + MP + ah = 0. dh σ

Поскольку при в > 0 справедливо равенство v ^e | _v=₀ = 0, для уравнения (11) имеем, что условию (5) соответствует

P⁽⁰⁾ = -М ^{—                                 (12)}

Теперь перейдем к эквивалентной динамической системе dh dξ dp dξ

βwp,

- p ² - µp - αh. σ

Здесь параметризация выбрана таким образом, что dz = vd^ .

Переход от уравнения (10) к динамической системе производится проще, последняя имеет вид

{ dv

• -77 = ^vw,

dξ

dw = -¹ w 2 - (3 + ⁴ : VW - A + ⁴) v 2 - w - V_:

dξ σ         σ           σ          B

Здесь также dz = vd^ .

На рисунке изображены динамические портреты системы (13) (слева) и системы (14) для случая a/B < 1 (справа). Отметим, что левый рисунок ранее уже встречался в работе авторов [21], однако там он фигурировал применительно к уравнению (2) без источника ( a = 0) и в несколько ином контексте.

Поскольку по смыслу рассматриваемой задачи (2), (3) нас интересуют неотрицательные значения v и h, представлены только правые полуплоскости. Можно видеть, что, несмотря на сходство фазовых портретов в первом квадранте, в четвертом квадранте имеются заметные различия в поведении фазовых траекторий, связанные с тем, что кривая второго порядка, на которой правая часть второго уравнения меняет знак (и, соответственно, фазовая траектория меняет направление движения относительно оси ординат), для системы (13) является параболой р2 + цар + a—h = 0, ветви которой направлены влево, а для системы (14) – гиперболой

¹ w ² +

σ

3 + — ^ vw + 2 + — ^ v ² + w + BB-v = 0

(соответствующие линии изображены на рисунке пунктиром). Вследствие этого сепаратриса, разделяющая узловой и седловой сектора, в первом случае огибает узловой сектор, приходит в особую точку (0, -ца) и порождает решение задачи (4), (5), принимающее положительные значения на конечном интервале (-h * , 0), которое

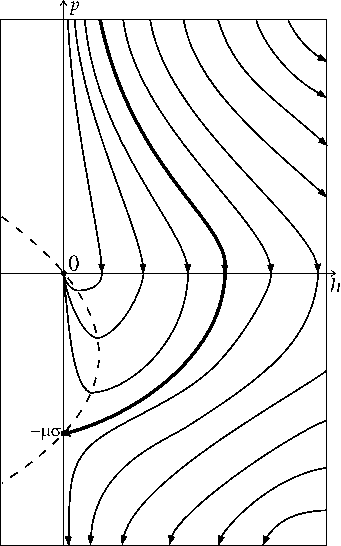
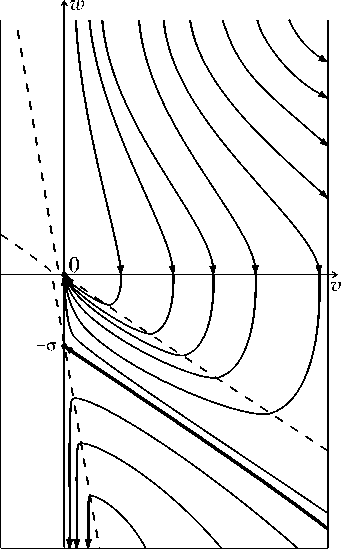
Фазовые портреты систем (13) и (14)

ограничено сверху (см. [22]); во втором случае данная сепаратриса является монотонной кривой, вдоль которой v меняется от +то до 0, и порождает она решение задачи (10), (5), стремящееся к бесконечности при s ^ —то. Отметим, что случай а/B = 1 приводит к решению, которое может быть представлено в виде явной формулы (см. ниже), случай а/B > 1 требует отдельного рассмотрения, которое выходит за рамки данной работы.

4.    Построение бегущей волны в виде ряда

Отметим, что степенные ряды используются для построения решений дифференциальных уравнений достаточно часто. Однако в современной математике классический метод степенных рядов [16], как правило, требует адаптации к исследуемой задаче. При этом коэффициенты могут быть представлены в виде самых разнообразных конструкций. Например, в работе Н.А. Сидорова и Д.Н. Сидорова [25] решение ОДУ приводится в виде степенного ряда с коэффициентами, зависящими от логарифмов. Отдельно упомянем метод специальных рядов [10] (см. также [7]).

Решение задачи Коши (11), (12) мы будем строить в виде ряда Тейлора

∞

P(h) = ^

n=0

p n ^h , n!

P n =

_d n p dh ⁿ

h=0

Из начального условия (12) следует, что р0 = —^а. Остальные коэффициенты ряда (15) определим, применяя к уравнению (11) дифференциальный оператор Dn[.] = dn/dhn |w=0. При n = 1 получим равенство п 2

вР о Р 1 + P 0 P 1 + ЦР 1 + а = 0,

σ

из которого выразим p ₁

Pi =    a ++

+(1 + ав )

При n = 2 и n = 3 имеем, соответственно,

=         2a2             =          6(2 +Зав )a3

P 2   а^ ³ (1 + ав )(1 + 2ав)’ P 3    а ² + 5 (1 + ав ) ² (1 + 2ав)(1 + 3ав)

На n –ом шаге имеем формулу

Е [1 + а в (n — k)]C k P k P n-k

Pn = k=------77----m------, n > 2.(18)

ад(1 + nав )

Коэффициенты p n , n > 1 однозначно определены и положительны при а >  0.

Пусть теперь а >  0 и а в > 1. В этом частном случае авторам удалось получить оценки радиуса сходимости ряда (15). Для этого будем пользоваться следующей леммой.

Лемма 1. Коэффициенты (16)–(18) можно представить в виде

P n = а+(1 + ав )

n a           n!qn ад2(1 + ав)   1+ nав1

n > 1,

где qn определяются из рекуррентного соотношения n-1

q 1 = q 2 = 1 ,

q n = d + а^в^^.n >  ²'

k =1

Доказательство. Лемма легко доказывается подстановкой (19) в (18).

□

В дальнейшем для большего удобства мы будем использовать именно это представление коэффициентов ряда.

Для исследования радиуса сходимости R воспользуемся формулой Адамара

R = —l L = lim

L     n →∞

n pn у n!'

В силу рекуррентного задания q n , непосредственно определить, чему равен радиус R довольно сложно. В этом разделе мы ограничимся его оценками, полученными с помощью следующих двух предложений.

Предложение 2. Для всех натуральных n > 1 справедливо неравенство q _n > 1.

Доказательство. Неравенство qn > 1 справедливо при n = 1,2. Базис индукции выполнен. Предположим теперь, что qi > 1 при i = 3, ...,n — 1. Пользуясь формулой (20), получаем неравенство n-1                         n-1                             n-1

q n = (1+ав )E_I^q+q ^-k в > (1+ав )Е_Г+^ ^(^ ав ) Е тт^ >¹- k =1                         k =1                             k =2

Предложение доказано.

Предложение 3. Существует константа M >  1 такая, что для всех натуральных п > 1 справедливо неравенство q _n <  M n^-1 /п.

Доказательство. Чтобы выполнялся базис индукции q1 < 1, q2 < M/2, необходимо положить M > 2. Предположим теперь, что qi < ------, i = 3,..., n — 1.

i

Следуя формуле (20), получаем оценку qn = (1 + ae) np qkqn-k < (1 + ов) Mn-1 np________1________.

ⁿ          k^ 1 + ков M        k^ (1 + ков)k(n — k)

Осталось показать, что существует константа M > 2, при которой выполняется нера- венство

n-1

n k=1

1           M

(1 + ков)k(n — k) ^_ (1 + ов)

В силу равенства

________1________=        ^{—( ов ) 2}       + ¹ +________1________

(1 + ков)k(n — k)   (1 + пов)(1 + ков)   nk n(1 + пов)(n — k) ’ левая часть (22) может быть преобразована как n-1

У п = n^

k=1

(1 + ков )k(n — k)

n-1               n-1

— (ов)2n у 1    , у 1 ,

1 + по в 1 + ков к 1 + по в п — к k=1             k=1

о )2 п у__1__+ (1 +__1)у

1 + пов 1 + ков V 1 + по в / к k=1

Оценим y n , используя следующую лемму (ее доказательство носит характер упражнения для студентов и для краткости опускается).

Лемма 2. Для любого ^ > 0 справедливо неравенство n-1 у k=1

<     + 1ln1±^(n-22

1 + Ц - 1 + {  {     1 + {

Отсюда при ов > 1 следует оценка

—овп П^-1 1     /1       1 А П ^-^ 1

^{У п} — 1 + пов к~р 1 + к "*" \    1 + пов / kzp к

2 у 11   1   1    2

1 + пов ^zp 1 + к ⁺ +1+ пов п п(1 + пов )

≤

1 + пав

(In n + 1)

\ 2 2/

< 1 + 2ав +

2 in n

1 + пав

+ 1 + г+пав

+ 1 - 1 + 2ав

n

+ 2 max n≥2

n(1 + пав )

; ln n „ + 1.

1 + пав

Получаем, что константа M существует и равна

M = (1 + а в ) | ------- + 2 max

\ 1 + 2а в     n>2

Предложение доказано.

ln n

1 + пав

+1) •

Добавим, что при ав = 1 значение M можно существенно уточнить. Действи- тельно, yn в этом случае запишется в виде n-1

У п = п^

k=1

(1 + к)к(п — к)

- n

1 + п

n-1

Е k=1

1 + к ⁺

(' ■.+.)11'

= (— ^Е п+1       1+к k=1

+

кГГ + 1

-

1V

n

(п + 2)(п — 1) (п + 1)п

+ п +

n-1

Е к + 1

k=1

Пользуясь неравенством (23), получим оценку уп < (п + 2)(п 1) + -2- (1 + inп) =    2    , 2 . + ElnJL.

(п + 1)п      п + 1 \2     2/ п + 1    п(п + 1) п + 1

Таким образом, при ав = 1 следует положить

M = 2 max n≥2

п +2

-

п + 1    п(п + 1)

, ²lnП ' п + 1

=2

п +2

-

п +1

2        2 in ^п "

п(п + 1) п + 1

n=6

46 , 4ln3 21+ 7

.

Константа M приближенно равна 2, 818.

Определим теперь интервал, в котором лежит радиус сходимости R. Из доказан- ных предложений следует двойное неравенство а^(1 + ав) I" — а 1     1    < pn = а^(1 + ав) I" — а 1    qn   < ац2(1 + ав)] 1+ пав   п!               |_а^2(1 + ав )_| 1+ пав

< а^(1 + а в ) Г aM I n 1 ^_ M     |_а^ ² (1 + ав )] п(1 + пав )

По известной теореме математического анализа о трех последовательностях предел L (см. формулу (21)) существует и удовлетворяет неравенству

α ≤ L ≤ αM ар?(1 + ав) — — ар?(1 + ав)

Тогда радиус сходимости ряда (15) лежит в интервале

R ∈

/а^ ² (1 + ав ) а^ 2 (1 + ав )

\ aM ’ a

Подводя итог данному разделу, скажем, что подобные исследования радиуса сходимости в указанных задачах публикуются впервые.

5.    Построение волны с экспоненциальным фронтом в виде ряда

Для построения и исследования решения в виде степенного ряда удобнее отказаться от замены s = ln z и рассматривать уравнение (6). В условиях предложения 1 оно имеет вид

„ 1 / а? (. 4 \ vv (    4\ v ² B . а                 , .,

⁺ _ ₍v ' ) ² + ^ + _) _ . ; ² . _) _ ⁺ A^ ₊ A— v = °.      (²⁴)

Для (24) имеем условия Коши

v(1) = 0, v ' (1) = -a.

Решение задачи (24), (25) интересует нас на интервале z Е (0,1]. Можно видеть, что (24) имеет особенность в точке z = 0. При этом из результатов качественного анализа следует, что vz^+Q ^ +^. Для того чтобы раскрыть указанную особенность, сделаем в (24) замену: введем новую искомую функцию f и новую независимую переменную ζ f = z2v, Z = Z - 1.

После подстановки и приведения подобных слагаемых и умножения на (Z + 1) ⁴ получим следующее уравнение:

ff '' + -( f ' ) ² + Zf ' + f ' + nf = 0.                        (26)

σ

Здесь A = B > 0, а > 0, n = а/B — 2 > -2. Условия (25) примут вид f (0) = 0, f'(0) = —a.                               (27)

Будем строить решение задачи (26), (27) в виде ряда по степеням Z = xexp(—Bt) — 1

∞n        n f (z ) = E fnr -f- = df

.

Z=o

Коэффициенты (26) определяются индукцией по n по использованной ранее процедуре. Из условий (27) нам известно, что f o = 0, f 1 = —a. Для нахождения f ₂ продифференцируем обе части (26) по Z и положим Z = 0. Разрешив полученное равенство относительно f 2 , имеем

Л = — ^(L+p).(29)

a + 1

И так далее. Пусть найдены коэффициенты до n включительно. Для нахождения f _-+1 продифференцируем обе части (26) n раз по Z и положим Z = 0. Получим соотношение

-11

( C- +   C-  j fkf-+2-k +   f-+1f1 + f-+1 + (n + n)f- = k=i        aa разрешив которое относительно fn+1, имеем формулу f-+1 =        ^ fCnk + C- 11 fk f-+2—k + 1 I

1 + na k^ \ a )          1 + na

Поскольку а > 0, значение f n+1 из (30) определяется однозначно. Локальная сходимость ряда (28) следует из ранее доказанных авторами теорем (см. [15]).

Интересным является вопрос о величине радиуса сходимости R. Можно ли утверждать, что R > 1? Положительный ответ на этот вопрос означал бы существование аналитического решения задачи (2), (3) в рассматриваемом случае при всех t >  0, 0 < x < exp(Bt). На момент написания статьи этот вопрос оставался открытым в общем случае. Однако в одном содержательном частном случае на него можно дать положительный ответ.

Предложение 4. Пусть a/B = 1. Тогда решение задачи (26), (27) является линейным и имеет вид f = —aZ • Если a/B < 1, то решение является выпуклым вниз; если a/B > 1, то решение является выпуклым вверх в некоторой окрестности точки Z = 0 .

Доказательство. Пусть a/B = 1. Тогда п = -1 и из (29) следует, что f ₂ = 0. Можно показать, используя (30), что отсюда следуют равенства / з = f ₄ = ... = f n = ... = 0, т.е. ряд (28) обрывается и решение задачи (26), (27) имеет вид f (Z) = f ₀ + f 1 Z = -aZ .

Если a/B > 1, то из (29) имеем f ₂ < 0, а в противном случае f ₂ > 0, что обеспечивает выпуклость решения соответственно вверх или вниз. Что и требовалось доказать.

Из предложений 1 и 4 следует, что при в = 1,a = B > 0 задача (2), (3) имеет решение aBx2 Z     aBx2 (x exp(—Bt) — 1)   „ u = - « + 1)2 =ep 2Bt)---- = ' exp(Bt)lexp(Bt) — 4    (31)

Решение (31) является при любом 0 < x < exp(Bt) положительным, аналитическим по t во всей области определения, поскольку представляет собой разность двух экспонент. Можно также видеть, что (31) неограниченно возрастает при 0 <  t <  то и 0 < x < exp(Bt). Напомним, что рассматривается (см. раздел 2) случай B >  0, т.е. когда тепловая волна движется вправо.

Заключение

В ходе проведенного исследования удалось подробно (с построением разложений в сходящиеся степенные ряды) исследовать точные решения, имеющие тип тепловой волны, распространяющейся по холодному (нулевому) фону с конечной скоростью, для нелинейного уравнения теплопроводности с источником. Одно из них является простой волной, которая движется с постоянной скоростью. Ранее авторами оно уже рассматривалось, однако здесь впервые установлен новый факт: получены достаточно точные оценки на радиус сходимости степенного ряда, в виде которого решение строится. Второе характеризуется экспоненциальным законом движения фронта и ранее нами не исследовалось. Для него получено условие, при выполнении которого степенной ряд обрывается и решение имеет простой и наглядный вид. Также был выполнен сравнительный качественный анализ двух ОДУ, к которым сводится построение указанных решений. Он позволил сделать содержательные выводы о свойствах решений.

Дальнейшие исследования в данном направлении могут быть связаны с построением оценки радиуса сходимости ряда (28) в общем случае. Также интерес представляет подробное (по аналогичной схеме) изучение других классов точных решений рассматриваемого типа, например, решения со степенным фронтом.

Исследование выполнено при финансовой поддержке РФФИ и Министерства по науке и технологиям Тайваня (проект № 20-51-S52003), а также РФФИ и Правительства Иркутской области (проект № 20-47-380001).