Точный порядок роста мажоранты в неравенстве Шварца - Пика для жесткости кручения

DOI:

Неравенства типа Шварца — Пика берут свое начало в классических трудах Пика [14], Каратеодори [13], Саца [19], Бернштейна [12] и др. Последние десятилетия эта тематика активно развивалась, ряд результатов по неравенствам данного типа можно найти в работах Рушевея [16; 17], Ямашиты [20], Авхадиева [7–10] и др. (см. также [2–4]). Основным объектом изучения в подобных неравенствах являются производные функций /, в общем случае локально голоморфных или мероморфных в некоторой гиперболической области Q С C и таких, что /(Q) С П С C. В работе [6], посвященной аналогам леммы Шварца для интегральных характеристик плоских односвязных областей, неравенства типа Шварца — Пика удалось распространить на физический функционал области, такой как коэффициент жесткости кручения. Ниже приведем основные определения и необходимые результаты из данной статьи.

Пусть Q — произвольная односвязная область в комплексной плоскости C. Жесткостью кручения (коэффициентом жесткости кручения) упругой балки с поперечным сечением Q называется функционал Р (Q), определяемый как решение следующей вариационной задачи (см. [11; 15]):

Р (fi) =

sup   2 rQ n(x)dxf ugc^q) rQ \^u\2dxdy '

где (x, у) E fi, C^fi) — пространство гладких функций с компактным носителем в fi. Общая теория кручения была разработана Сен-Венаном. Согласно предложенной им формуле:

Р(fi) = 2 Д у dx dy , Ω где у = у(х, у) — решение краевой задачи Дирихле для уравнения Пуассона Ду = — 2 с краевым условием f|dQ = 0. Функцию у называют функцией напряжений. Изучению свойств данной функции посвящено множество работ (см., например, [5; 18]). Эквивалентность двух определений жесткости кручения доказана в [15]. Поскольку функционалы, определяемые посредством краевых задач, являются трудно вычислимыми, важной проблемой математической физики является получение оценок для них через более простые, геометрические, характеристики области. В 1998 г. Ф.Г. Авхадиевым было установлено, что жесткость кручения эквивалентна конформному и евклидовому моменту инерции относительно границы [1].

Далее пусть fi — произвольная односвязная область в C и 0 E fi. Согласно теореме Римана существует функция / : Д ^ fi, такая что /(0) = 0. Пусть fi _r — образ круга Д _г = { Z E C : | С | < г } при отображении функцией / для всякого г E (0,1), то есть fi _r = {z E fi : z = /(Z), | Z | < г, г E (0,1) } . В [1] сформулирован аналог теоремы Шварца — Пика для Р (fi), а именно доказана теорема.

Теорема. Пусть Р(fi) < то и 0 < г < 1. Тогда справедливы следующие неравенства dP (fir)

dr

<

1—7^Р (fi),

и для всякого т E N

^Р (fi _r ) y^2m+1)<

(2т + 1)!Р (fi) (1 — г ² ) ^{2 т +1}

т /  \ ²

S (т)"

.

Оба неравенства в данной теореме являются строгими. Например, для первого неравенства это означает, что для любой константы с > 0 не существует области fi, такой что

dP (fi _T )      сг ³

(0 < г < 1).

dr ^— 1 — г² ’

В этом легко убедиться, тем не менее, ниже мы покажем, что порядок точности приведенных оценок улучшить нельзя. В этом смысле полученные оценки являются асимптотически точными.

• 1 . Основные результаты

Теорема 1. Для любого г0 E [1/2,1) существует область fi = fi(г0), содержащая в себе точку z = 0, такая что dP (fir (го))      >   со dг      г=го    1 — г0 ’ где со = 27П35.

Доказательство. В качестве области П рассмотрим круг единичного радиуса, граница которого проходит близко к началу координат (рис. 1).

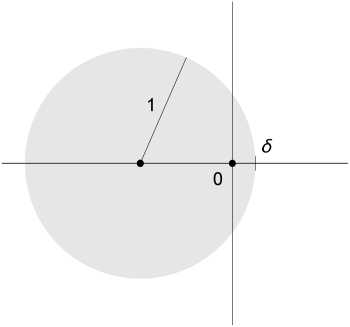
Рис. 1. Область Ω

В [6] доказана формула

Р (Q _r )

то          [ 2 ]

П Е ^ ^{2 n} Е n =2 а =1

n — а

Е авап— в в=а

где а ^ — коэффициенты разложения в ряд Тейлора конформного отображения f : А ^ ^ Q. Воспользуемся этой формулой в качестве примера ее практического применения для вычисления Р (П _т ). Построим отображающую функцию f(г), которая переводит единичный круг А в область П с соответствием f (0) = 0:

f (г ) =

г — (5 — 1)

1 — (5 — 1)г

+ 5 — 1.

Разложим f (г ) в ряд по степеням г и запишем общий вид коэффициента a _k при г ^k :

f (г) = ^Е г ^k ^—1) ^k—1 (1 — 5 ) ^{k— 1} + ( — 1) ^k (1 — 5) ^{k +1} ) , k =1

то есть ak = (—1)k—1 (1 — 5)k—1 + (—1)k (1 — 5)k+1.

Вычислим произведение a _k a _n—k :

a k a n - k = ( ( - 1) ^{k —1} (1 — 5) ^{k —1} + ( — 1) ^k (1 — 5) ^{k +1} ) (( — 1) ^{n — k —1} (1 — 5) ^{n — k —1} + + ( — 1) ^{n — k} (1 — 5) ^{n — k +1} ) = ( — 1) ^{n —2} (1 — 5) ^{n —2} + 2( — 1) ^{n —1} (1 — 5) ⁿ + + ( — 1) ⁿ (1 — 5) ^{n +2} = ( — 1) ^{n —2} (1 — 5) ^{n —2} ( 1 — (1 — 5) ^{2 ) 2} .

Обозначим y = 1 — 5, тогда согласно формуле (2)

то        ^[ 2 ^] n — а

Р (п ) = П Е r ^{2 n} Е Е ( — 1) ^{n —2} Y ^{n —2} (1 — Y ² ) ²

• ²    n =2    ал в = а

Поскольку произведение коэффициентов а ^ а _п— к не зависит от индекса суммирования, его можно вынести из-под знака суммы. Имеем

⃒                                                                                           ⃒ ₂

п — а

£ Y ^{n —} 2 ( - 1) ^{п —} 2 (1 - Y 2 ) 2 = | Y ^{n —} 2 ( - 1) ^{п —} 2 (1 - Y 2 ) 2 (^ - 2а + 1) |2 . β = α

Следовательно,

^                            [ 5 ]

Р(Ю г ) = ^П £ r ^{2 n} Y ^{2 n —} 4 (1 - Y ² ) ⁴ £ I n - 2а + 11 ² .

п =2                    а =1

Имеем

(п ² - 1)

Р (Ю г ) = 2

£ Г2пу2п—4(1 - Y2)4 • п=2

Вынесем все множители, не зависящие от п, из-под знака суммы, получим

24 ∞

РМ) = --',   £n(n2 - 1)(гу)2п.(3)

2  от4“ п=2

Введем обозначение t = ( t y ) ² и вычислим сумму в последнем выражении для Р(Ю _г ):

∞∞∞

£ п(п2 - 1)tn = £ n3tn - £ ntn.(4)

п=2               п=2

Используя известную формулу для геометрической прогрессии

∞

1 + t +1 ² +... = £ t ⁿ n =0

- t

дифференцированием по t получаем

∞

^£ nt n ^-1

п =1

1            го

■  ■• ^ £nt п=1

t                  _п t

(T - tp ^ П =2 ^nt =(F - tp - ^t.

Аналогично последовательным дифференцированием вычисляем и первую сумму в (4). Окончательно имеем

_6t 2

£t,Xn -1        ■ ■ ■ n=2

Возвращаясь к прежним обозначениям и применяя формулу (3) для вычисления жесткости кручения Р(^ _г ), получим

Р (Ю г )

п(5 - 2) ⁴ 5 ⁴ t ⁴ 2((5 - 1) ² т ² - 1) 4 ■

Вычислим производную

^ Р(Ю г ) ) ‘ =

4п(2 - 5) 4 5 4 (5 - 1) ² т

£Т-£5-lp72^ ■

Достаточно показать, что для каждого фиксированного т ₀ G [2 ,1) приведенная выше область Q существует. Существование области Q равносильно в нашем случае существованию величины 5. Положим 5 = 1 — т 2 . Тогда

4п(1 + т 2 ) ⁴ (1 — т 2 ) ⁴ т 5 = 4п(1 + т 2 ) ⁴ (1 — г 0 ) ⁴ г 0 =     4п(1 + т 0 ) ⁴ т 0      - с

^{(1 — т} 0 ^{) 5            (1 — т} 2 ^{) 5 (1 +} ^ 2 ^{+ т} 4 ^{) 5     (1 — т} 0 ^{)(1 +} ^ 2 ^{+ т} 4 ^{) 5} ” ^{(1 — т} 0 )'

Определим константу с из условия неравенства. Имеем

4п(1 + т 2 ) ⁴ т 5    4п(1 + т ^ ) ⁴ т 0    4пт 5     4п п

(1 + т0 + т4)5 -      35      - "з5" - 2535 = 1944’ то есть в качестве константы с можно взять число 1944.

Теперь рассмотрим случай производных порядка п >  1. Вычислим производную п-го порядка для функции Р (Q _r )/т ⁴ . Для этого приведем ее к виду

Р (П_г) _ п(5 — 2) 4 5 4       1

т4            2        (1 — аг2)4 ’ где а = (5 — 1)2. Таким образом, необходимо вычислить производную п-го порядка для функции 1/(1 — ат2)4. Для этого предварительно разложим ее в ряд, а затем продифференцируем. Перепишем нашу функцию в виде 1/(1 — t)4 (t = ат2). Тогда, последовательно дифференцируя функцию 1/(1 — t), получим

1                                  го

1---1 = 1 + t + t ² + ... = 5 2 t^k ,

(1 — t) ²

2 (1 — ) 3

2 • 3 (1 — t) ⁴

(1 — ат ² ) ⁴

∞

^V kt ^{k -1} , к =1

2 k(k — ц^^-2, к =2

^V к(к — 1)(^ — 2)t ^k-3 . к =3

Окончательно имеем

∞

- V (к + 3)(к + 2)(к + 1)а ^к т ² .

• ⁶ k=0

Последовательно дифференцируем полученный ряд

( (

(

₍₁ —^2)4 ) ' =6 22 ( ^к + 3)( ^к + ² )( ^к + ¹ )а ^{к 2к} т ^2к-1 -

,,   ¹₂₁₄ )" = ^{1 V} (к + 3)(к + 2)(к + 1)а ^к 2к(2к — 1)т ^{2 к -2} ,

⁽¹ — ^{ат 2 )4};     ⁶ к =2

1        ⁾ ‘‘‘

(1 — ат ² ) ⁴

∞

- У(к + 3)(к + 2)(к + 1)а ^к 2к(2к — 1)(2к — 2)т ^{2 к -3}

к =3

и т. д. Имеем

, 1

(1 — ar ² ) ⁴

^{( n )}

^                       n

6 £ a^k(k + 3)(k + 2)(k + 1) ^ (2k - J + 1)r ^{2 k - n} .

k=n                          3 =1

Таким образом, получаем

( ад yn)

∞

= £ (S — 2)454(5 — 1)" £ tk k=n

-

^ (k + 3)(k + 2)(k + 1) П (2k — j + 1), 3=1

где t = (5 — 1) ² r ² .

Мы должны показать существование константы с >  0, такой что

(,      ) ^{( n )}

с

^— (1 — Г о ² ) ^п ,

Г о G 2, У ,

n G N.

Рассмотрим сумму в выражении производной n-го порядка:

∞

£ t ^k - ^ (k + 3)(k + 2)(k + 1)2k(2k — 1) • ... • (2k — n + 1).             (5)

k=n

Так как

2k — k,

2k — 1 -k — 1,

2k — n + 1 — k — n + 1 = k — (n — 1), то выражение (5) преобразуется следующим образом:

²² t ^k - ^ (k + 3)(k + 2)(k + 1)2k(2k — 1) • ... • (2k — n + 1) — k=n

• — 52 t ^k - I (k + 3)(k + 2)(k + 1)k(k — 1) • ... • (k — n + 1) = k=n

= t^ 52tk-n(k + 3)(k + 2)(k + 1)k(k — 1) •... • (k — n + 1) = k=n t^ (n + 3)!t

= (1 — t) ^{n +4 —} (1 — t) ^{n +4} .

Имеем

/ P (Qr (ro)) \(n) — n(5 — 2)454(5 — 1)" (5 — 1)nrg ro4    )    —      12(1 — (5 — 1)2r0)"+4

Положим 5 = 1 — r0 и покажем, что существует константа с > 0, такая что п(1 + r0 )4r0"

12(1 — r 0 ) ⁿ (1 + r 0 + r 4 ) ^{n +4} “ (1 — r 2 ) ⁿ

Из (6) следует, что

• <    nr 3 ⁿ (1 + Г 2 ) ⁴

^С “ 12(1 + т 0 + т- 04 ) ^и + ⁴ '

Определим константу с из условия неравенства для 1/2 <  т ₀ <  1

Пт 3 ” (1 + т 0 ) ⁴       ПГ д ^П (1 + т 0 ) ⁴       ПГ д ”             П

12(1 + т 2 + т ⁴ ) ^и + ⁴ -     12 • 3 ^И + ⁴    - 12 • 3 ^И + ⁴ - 12 • 2 ^{3 п} • 3 ^И + ⁴ '

Следовательно, за константу с можно взять число ₂ 3_п+ ^П _{3 п+}5 . Таким образом, нами доказана теорема.

Теорема 2. Для любого т0 Е [1/2,1) существует область fi = Q(r0), содержащая в себе точку z = 0, такая что где с =

π

2 3 п +2 3 п +5 .

Р (fi (т о )) )^Н

Г ⁴

т = т о

≥

С

(Т - то^,

Замечание. Следует отметить, что утверждение теоремы 2 справедливо для всякого произвольного п Е N, в отличие от неравенства (1), где результат сформулирован лишь для нечетных производных.

Автор благодарит профессора Ф.Г. Авхадиева за проявленный интерес и постоянное внимание к работе.