Тонкопроволочные излучающие структуры с двойной симметрией

Тонкопроволочные излучающие структуры с двойной симметрией достаточно часто встречаются в электродинамических задачах (различные виды широкополосных вибраторных антенн, многозаходные спиральные структуры и т. д.). Учет симметрии позволяет существенно упростить решение внутренней электродинамической задачи, которая сводится к совокупности независимых интегральных уравнений (ИУ) Фредгольма первого рода [1; 2]. Это существенно проще решения системы ИУ, возникающей в общем случае. Более того, на практике часто встречаются случаи (азимутально-независимое возбуждение вибраторных антенн, синфазное или противофазное возбуждение двузаходных спиралей), когда необходимо решение неполного набора ИУ, что дополнительно упрощает задачу.

В настоящей статье показано, что на основе интегральных представлений электромагнитного поля (ИП ЭМП) тонкопроволочной структуры (ТПС) [3] можно достаточно просто строить математические модели множества излучающих структур с двойной симметрией. В ряде случаев такой подход приводит к моделям сеточного типа. При малых расстояниях между проводниками такие модели эквивалентны моделям со сплошными поверхностями, строгий расчет которых приводит к более сложным в аналитическом и численном плане системам ИУ с особенностями логарифмического и гиперсингулярного типа.

В качестве примера в данной статье рассмотрены две многозаходные эллиптические спиральные антенны: двузаходная и четырехзаходная с двумя пассивными заходами. Для них вычислены распределения токов вдоль проводников, зависимость входного сопротивления в диапазоне частот, а также нормированные диаграммы направленности.

1. Основные выражения

С учетом выражений, приведенных в [4], ИП ЭМП для структуры с двойной симметрией принимает вид

F ( r ) = Е£, I e ( l ') K ⁽ F ) ( r , r ' e ; ^e j ) dl ‘ , F "  E , H .           (1)

e ^Lj

Здесь e = g , j – индекс-вектор элемента структуры; g = { s i , s 2 } - индекс-вектор группы; s 1 =1 . N -индекс группы по симметрии первого типа ( s 1 -группа); s 2 =1... N 2 — индекс группы по симметрии второго типа ( s 2 -группа); б j - радиус проводника; j = 1 . N e - индекс элемента в группе g , N_e – соответствующее число элементов; I _e ( l ) – функция распределения тока на проводнике L e , r ' e = r ' e ( l ') = S ' S 2 r ( l 9, l 'б L j                         (2)

s ₁ s ₂ g ₁ , j

- уравнение образующей L e ; S ^ ) - матрицы симметричных преобразований образующей j -го проводника основной группы g 1 . Ядра K ^{( F} ) определены выражениями [3]:

K ^E

W

VV -     -,

W c l e k ²

ik

I ( d . B ) ,

K H =( d e X l ' e ) B.

Заметим, что элементы с одинаковыми индексами в разных группах являются подобными с единичным коэффициентом подобия, поэтому в (1) L j = L e , б j = s e .

Совокупность независимых систем интегральных уравнений Фредгольма первого рода получается аналогично [5]:

^E l ) = Zf L ^⁽ l'KKП g^⁽ l , l)d»' l ' Li- ⁽⁴⁾ Здесь:

^K g ? g i ⁽ l , ' ')=

= Z 'g^^v ' ' - - g , j ⁽ l ), g ⁽ ^i W g 1 g '

E (in) ( l ) = -eV Г 1 (гУ )) ■ E ⁱⁿ (/ . ) ' W + 1 , g , i         ^L g > j           g > j J ^g , ^g

g

Z = z ⁽¹ ) z ⁽²⁾,   w = w ⁽¹⁾ w ⁽²⁾,   t = 1,2.

Константы Z ⁽ t ) и ядра симметричных преобразований W ^{( t )} определяются типом соответствующей симметрии.

Дискретизированная версия ИП ЭМП может быть записана по аналогии с [3]:

F ( r ) = £ I s K ⁽ F ) ( r , r s ; S j , A j ),   F = E , H .                 (6)

s

S _j

– весовые коэффициенты,

- s = - s ( l ) = r s + l s l ; l e [ -A j /2, A j /2]                     (7)

- уравнение сегмента S j ; r * = ( r _{fc + 1} + r . ) / 2, l . = = ( r . ₊ i - r . )/ A . - соответственно, радиус-вектор центра сегмента (точка коллокации) и единичный вектор касательной на сегменте; A . - длина сегмента.

Для структуры с двойной симметрией объекты группы g можно получить из объектов основной группы g ₁ с помощью преобразования (2).

Совокупность блочных СЛАУ будет иметь вид:

У I— K     = E (in) .                             (8)

g,j' g,j,g,j'        g,j j'

Здесь:

E Н= чУ[1 ( гУ ) ■ Е ⁽™> (гУ) 1 W ^-1;

g,j        z^. g,j           g,j J g,g g'

(9) J <- — = y l ( r *4 ■ K ^E ( r^ , r .; Sj., Aj .) W „-1.

g,j,g,j Д-i      g,j           g ,j’ g,j’ j ’ j        g,g g' L                 1                   J

После определения из (8) неизвестных амплитуд I s токи на сегментах вычисляются по формуле ¹ . = Z I gj W -F                            ⁽¹⁰⁾

g

Полученные выражения обладают большой степенью общности и могут быть легко переписаны на случай структур с тройной симметрией. При этом выражения для тонкопроволочной структуры с одиночной симметрией можно получить из (1)–(10) с помощью условий:

g={s}, Sˆ(2) =Eˆ, s=s1, N1=S, s 2

а выражения для совокупности тонкопроволочных проводников можно получить из (1)-(8) с помощью условий:

g = {}, S(1)= s(2) = E, F = F, F = E, I, K. ,                        ,            ,            ,, s1s2

Здесь E ^ˆ – единичная матрица.

Далее рассмотрим применение представленных выражений для расчета многозаходных эллиптических спиральных излучателей.

• 2.    Геометрия исследуемых структур

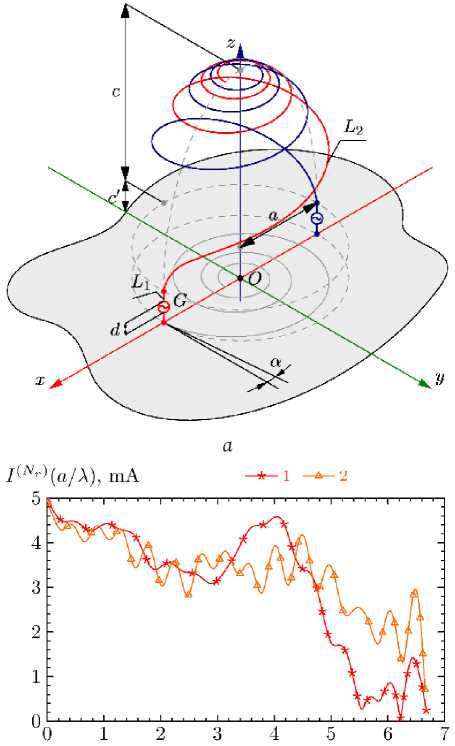
Рассматриваемые дву- и четырехзаходный эллиптические спиральные излучатели (далее по тексту ЭС-2 и ЭС-4 соответственно) являются развитием моделей, представленных в [4; 6]. Геометрия ЭС-2 отражена на рис. 1. Основная группа содержит два проводника: активный вибратор L ₁ и эллиптическую спираль L ₂ с соответствующими параметрическими уравнениями образующих:

L 1 : r 1 ( l ) = x a + z l , l e [0; L 1 ],                               (11)

L ₂ : r ₂( l ) = x a cos( Z ) P ( Z ) + y a sin( Z ) P ( Z ) +

+ z ⁽ c^ ¹ -p ⁽² Z ) + c' ),

p ⁽ Z ) = exp ^{( -а}УЛ = ф ^{( l} ), ^{l e [0} ; L 2 ]•

Здесь ф ( l ) - функция, получаемая методом обратной интерполяции функции

ф

l ( ф ) = J | d r ₂ ( Z )/ dZ | d Z ,                                     (12)

L 1 = c ' , L 2 = l(2 n N l ) - длины соответствующих образующих; c - смещение эллипсоида вдоль оси Oz , N - число витков спирали; а - угол намотки плоской спирали, являющейся проекцией L ₂ на xOy ; a и c – полуоси эллипсоида. В центре L ₁ имеется разрыв длиной d ^ X , содержащий генератор G , создающий напряженность электрического поля E ^{( in )}, касательная компонента E_l ^{( in )}

б

Рис. 1. Многозаходный эллиптический спиральный излучатель ( а ), сравнение амплитуд тока ЭС-2 и ЭС-4 для а / X = 0,5 ( 6) Fig. 1. Multi-pass elliptical spiral radiator ( a ), comparison of current amplitudes ES-2 and ES-4 for а / X = 0,5 ( b )

которой на образующих проводников отлична от нуля только в области зазора, где она равна E r = = E exp( i v )/ d ; E и V — ЭДС и фаза генератора соответственно. Учет экрана, расположенного в плоскости xOy , производится методом зеркальных отображений [7] ( s 1 -группы), а s 2 -группы получаются поворотом основной группы проводников вокруг оси Oz . Таким образом, матрицы преобразований в (2) приобретают вид

	10   0
S (1 ) =	01   0
5 1
	v 0 0   ( - 1)( s 1 - 1)

S (2 ) =	cos ac s 2	sin a s 2	0
	- sin ac	cos a	0
s 2	s 2	s 2
	0 V	0	1 /

Здесь s 1=1,2; as = 2п(s2 -1)/ N; N — число пово- ротов.

Константа Z и ядра преобразований W±1 приобретают вид z = 1/72N, w4 = z(-1)(s 1 -1)(s 1-1) x x exp(+2ni(s2 -1)(s2 -1) / N).

Полагая N = 2 и N = 4, получаем группы проводников, необходимых для расчета ЭС-2 и ЭС-4. В случае металлического экрана ЭДС комплексные амплитуды E (, N ) генераторов ЭС-2 и ЭС-4 будут определяться формулами:

E g ²⁾ = ( — 1) ^{5 1} exp( п r ),

Eg4) = (-1) s1 mod( r ,2) exp( п s 2), где mod(r,2) - остаток от деления на 2, учитывающий, что второй и четвертый заходы ЭС-4 являются пассивными. Подстановка последних соотношений в (8) приводит к необходимости расчета для ЭС-2 только СЛАУ при s 1=1, s2 = 1, а для ЭС-4 - СЛАУ с s 1=1, s2 = 2, что существенно сокращает время расчета.

3.    Результаты численного моделирования

При численном моделировании основным параметром будем считать полуось a эллипсоида. Путем изменения отношений с' / a , с / a , a , N в некоторых пределах были получены их оптимальные значения с точки зрения входного сопротивления и диаграммы направленности излучающих структур. Моделирование осуществлялось в диапазоне a / X е [0,2; 0,7].

Для ЭС-2 оптимальными оказались следующие значения: с' / a = 0,35, с / a = 4,0, a = 5 ° , N =4,5. Результаты расчета входного сопротивления при этих параметрах показаны сплошной линией на рис. 2. Из графиков видно, что равномерность входного сопротивления сохраняется в диапазоне 0,3... 0,7 X , а чисто активное сопротивление равное 180 Ом реализуется при a / X® 0,55. Результаты расчета нормированных диаграмм направленности для оптимальной геометрии ЭС-2 представлены на рис. 3, a . Видно, что осевое излучение наблюдается в диапазоне 0,3... 0,55 X , а наибольший уровень боковых лепестков зафиксирован в диапазоне 0,45...0,5 X .

Для ЭС-4 оптимальными оказались следующие отношения: с' / a = 0,35, с / a = 4,0, a = 4 ° , N =4. Результаты расчета входного сопротивления для оптимальной геометрии показаны пунктирной

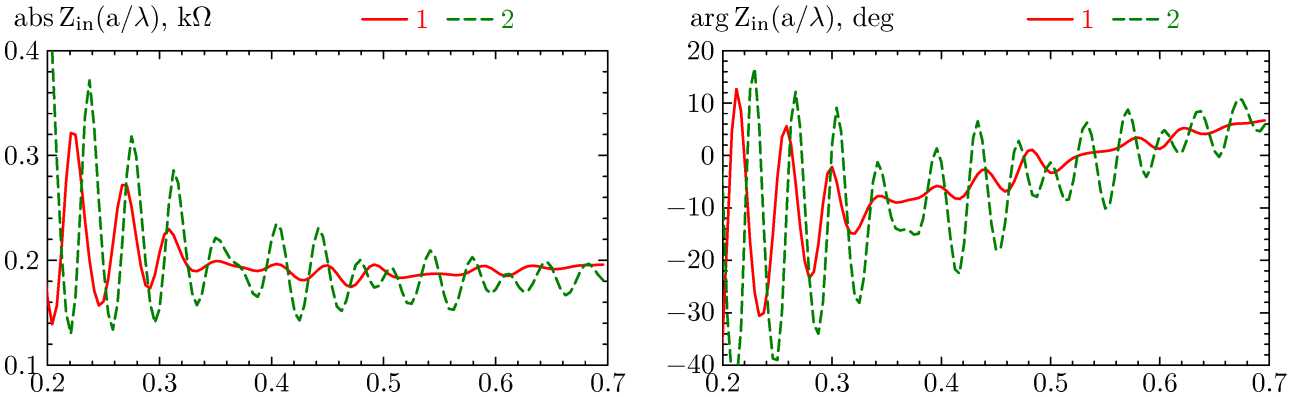
а                                                    б

Рис. 2. Результаты расчета модуля ( а ) и фазы ( б ) входного сопротивления: 1 – ЭС-2; 2 – ЭС-4

Fig. 2. Results of calculating the module ( a ) and phase ( b ) of the input resistance: 1 – ES-2; 2 – ES-4

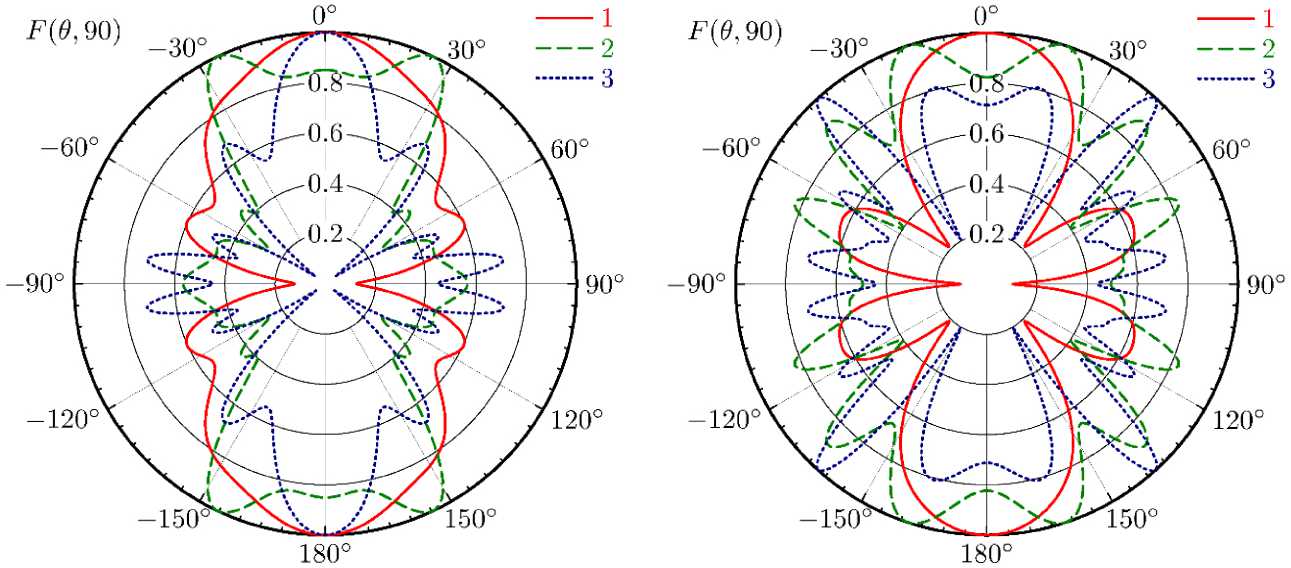
Рис. 3. Результаты расчета диаграмм направленности для 1 - a / X = 0,3; 2 - a / X = 0,425; 3 - a / X = 0,55: а - ЭС-2; б - ЭС-4

Fig. 3. Results of calculating the radiation patterns for 1 - a / X = 0,3; 2 - a / X = 0,425; 3 - a / X = 0,55: a - ES-2; b - ES-4

линией на рис. 2. Результаты расчета диаграмм направленности отражены на рис. 3, б .

Заключение

Таким образом, в статье рассмотрен вопрос построения математических моделей тонкопроволочных излучающих структур с двойной симметрией. Из тонкопроволочного ИП ЭМП получен набор СЛАУ для расчета амплитуд токов на сегментированных образующих. Показано, что учет двойной симметрии структуры существенно упрощает внутреннюю электродинамичскую задачу.

В качестве примера в статье рассмотрены два спиральных излучателя (двузаходный и четы-рехзаходный). Для данных структур вычислены распределения токов вдоль проводников, зави- симость их входного сопротивления от радиуса структуры, а также нормированные диаграммы направленности.

В заключение отметим, что на основе представленных в статье выражений можно достаточно просто строить математические модели спиральных антенн, используя при этом совокупность тонких проводников, в результате чего получаются модели сеточного типа. При малых расстояниях между проводниками такие модели эквивалентны моделям со сплошными поверхностями. При этом в ядрах получаемых систем ИУ не возникает особенностей логарифмического и гиперсингулярного типа, что упрощает численное моделирование. Также при наличии у излучающей структуры различных типов симметрий ее электродинамический анализ существенно упрощается.

Финансирование

Данное научное исследование проводится при поддержке Фонда содействия инновациям по программе «УМНИК» по теме «Разработка программы для расчета излучающих структур с учетом их симметрии» в рамках договора № 157 ГУЦЭС8-D3/56497 от 24.12.2019.