1.    Introduction and Preliminaries

A systematic study of topological indices is one of the most striking aspects in many branches of Mathematics with its applications and various other fields of science and technology. Several different topological indices have been investigated so far, most of them useful topological indices are distance based or degree based. This indices may be used to

• ^# The first author supported by the TEQIP Competitive Research Grant: VTU/TEQIP 3/2019/321 Dated 10 ^th December 2019.

• © 2020 Hemavathi, P. S., Lokesha, V., Manjunath, M., Reddy, P. S. K. and Shruti, R.

derive the quantitative structure property relationship (QSPR) or quantitative structure activity relationship (QSAR). Topological index to correlated the physico-chemical properties of chemical compounds with their molecular structure. Topological indices are the numerical value associated with chemical constitution for correlation of chemical structure with various physical properties, chemical reactivity or biological activity.

The third Zagreb index

M a ( G )= E I d G ( u ) - dGM

(1 . 1)

uveE ( G )

was introduced by Fath-Tabar in [1].

The harmonic index H ( G ) is introduced in [2] and is defined as:

H ( G ) = E

uv ^ E ( G )

d u + d v

(1 . 2)

Unfortunately, another degree based graph invariant has not attracted any attention in the literature of Mathematical Chemistry for more than forty years. In view of this fact, Furtula et al. [3] named it as forgotten topological index and is defined as:

F ( G ) = E [d G (u )² + d G ( v ) ² ] .

(1 . 3)

uv ^ E ( G )

The inverse sum index [4] is given by i (G) = E

d u d v

uv ^ E ( G )

d _u + d _v

(1 . 4)

For more details on this important topological indices, we refer to [5, 6]. According to the article in [7], both first and second Zagreb indices give greater weights to the inner vertices and edges, and smaller weights to outer vertices and edges which oppose intuitive reasoning. The second modified Zagreb index is:

^m M 2 (G) = E

uv ^ E ( G )

(1 . 5)

Among 148 discrete Adriatic indices [8, 9], we considered symmetric division deg discrete adriatic index. The symmetric division deg index is defined as (see [10]):

SDD ( G )= E

d ² _u + d _v ²

uv ^ E ( G )

(1 . 6)

The subdivision graph S ( G ) is the graph obtained by replacing each of its edge by a path of length 2 or equivalently, by inserting an additional vertex into each edge of G .

The semi total point R ( G ) graph is obtained from G by adding a new vertex corresponding to every edge of G and by joining each new vertex to the end vertices of the edge corresponding to it.

Boron nanotubes: In last 20 years, various type of boron containing nanomaterials. Boron nanomaterials have been considered as excellent material for enhancing the characteristics of optoelectronic nano devices because of their broad elastic modulus, high melting point, excessive conductivity. These materials can carry excessive emission current, which recommends that they may have great prospective applications in field emission area [11]. Boron nanomaterials some best properties such as excessive resistance to oxidation at high temperatures, great chemical stability and are stable broad band-gap semiconductor [12, 13]. Moreover, the extensive range of boron nanomaterials themselves could be the building blocks for combining with other existing nanomaterial to designe and create materials with new properties. The boron triangular nanotube was created in 2004 [11] and obtained from a carbon hexagonal nanotube by adding an extra atom to the centre of each hexagon. Also, a special boron nanotube was fabricated from a carbon hexagonal nanotube in 2008, by adding an extra atom to the centre of certain hexagons [14, 15]. This nanotube is designed by generating a mixture of hexagons and triangles called boron-α nanotube. These nanotubes are important materials for optical, electronic, bio and chemical sensing applications. The comparison study about some computational aspects of boron triangular and boron-α nanotubes has been investigated in [16]. The 3D perceptions of boron triangular and boron-α nanotube are presented in the Fig. 1.

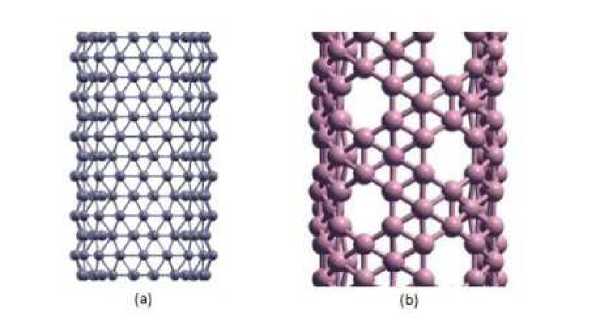
Fig. 1 (a) 3D-perception of boron triangular nanotube, (b) 3D-perception of boron-a nanotube.

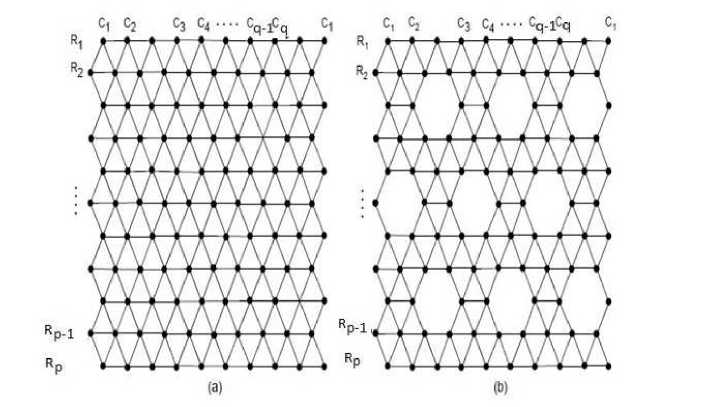
Fig. 2 (a) 2D-sheet of boron triangular nanotube BT [p, q], (b) 2D-sheet of boron-a nanotube BA[p, q].

Recently Jia-Bao, Hani Shaker and et al. [17] worked on topological aspects of boron nanotubes. Motivated from these works, we compute the third Zagreb index, harmonic index, forgotten index, inverse sum index, modified Zagreb index and symmetric division deg index by applying subdivision and semi total point graph for boron triangular and boron-α nanotubes.

This paper is organized as follows: In Section 2, we get topological indices of boron triangular nanotube, subdivision and semi total point graph of boron triangular nanotube. In Section 3, the topological indices of boron- α nanotube, subdivision and semi total point graph of boron- a nanotube BA(X )[ p, q ] are obtained. Finally, in Section 4, we presented the topological indices of boron- α nanotube, subdivision and semi total point graph of boron- α nanotube BA ( Y )[ p, q ] .

2. Boron triangular nanotube, subdivision and semi total point graph of boron triangular nanotube

We denote the molecular graphs of boron triangular and boron- a nanotubes by BT [ p, q ] and B A [ p, q ] respectively, where p is the number of rows and q be the number of columns in 2 D sheet of BT [ p, q ] and BA [ p, q ] as shown in the Fig. 2. Then boron- a nanotubes can be categorized into two classes with respect to p , denoted these classes as BA(X )[ p, q ] and

BA(Y )[ p,q ] .

Table 1. The order and size of triangular boron nanotubes Molecular graph BT[p, q] S = BT[p, q]    R = BT[p, q] Order            3 p 2 q        3q(2p — 1)     3q(2p — 1) Size            3 q (3 p -2)     3q(3p - 2)         9 q (3 p -2)

Theorem 2.1. Consider the boron triangular nanotube BT [ p, q ] , where p ^ 3 and q is

even, then

•    M 3 ( BT [ p,q ]) = 12 q, •    H(BT [ p,q ]) = 3 pq +3 q + 6 q - 2 q, 4     4    5 •    F(BT [ p, q ]) = 324 pq - 864 q + 96 q + 312 q, •    I(BT [ p,q ]) = 27 pq - 36 q + 6 q +72 q, 25 •    m M 2 (BT [ p,q ]) = 1 pq - 1 q +    q + 1 q, 8     3    16    4 •    SDD(BT [ p, q ]) = 9 pq - 24 q + 6 q + 13 q.

<1 Consider the boron triangular nanotube G = BT [ p, q ] . There are three edge partitions corresponding to the degree of end vertices which are presented as E 4 , 4 = {uv E E g | d u = 4 , d v =4 } , E 4 , 6 = {uv E E g | d u = 4 , d v = 6 } and Е б , б = {uv E E g | d u = 6 , d v =6 } .

Therefore, we have | E 4 , 4 | = 3 q, | Е 4 , б | = 6 q and | Е б , б | = ^3q(3p 8) . The respective edge partitions are shown in Fig. 3 in which edges belong to E 4 _, 4 , E 4 _, 6 and E 6 _, 6 respectively. Hence applying the topological indices definitions (Equation (1.1) to (1.6)) we get required results. >

Theorem 2.2. Consider the subdivision graph of boron triangular nanotube BT [ p, q ] , then

• •    M 3 ( BT [ p, q ]) = 36 pq + 24 q - 72 q,

• •    H(BT [ p,q ]) = 4 pq + 4 q - | q,

• •    F(BT [ p, q ]) = 360 pq + 240 q - 720 q, 27

• •    I(BT [ p,q ]) = y pq + 16 q - 27 q,

• •    ^m M 2 (BT [ p,q ]) = | pq +2 q — I q,

• •    SDD(BT [ p, q ])=30 pq + 30 q — 60 q.

• < 1 Consider the subdivision graph of boron triangular nanotube S = BT [ p, q ] . There are two edge partitions corresponding to the degree of end vertices which are presented as E 2 , 4 = {uv E E s | d u = I , d v = 4 } and E 2 , 6 = {uv E E s | d u = I , d v = 6 } .

Theorem 2.3. Consider the semi total point graph of boron triangular nanotube R = BT [ p, q ] , then

• М з ( ВТ [ p,q ])=7I q + 90 pq — 180 q + I4 q,

• •    H(BT[p, q]) = q + 9pq — 18q + 3q + 3q + 3pq — q, 5     7      7     8    58

• •    F(BT [ p, q ] = 816 q + 133I pq — I664 q + 384 q + 1I48 q + 1I96 pq — 3456 q,

• •    I(BT[p, q]) = 93q + 193q — ^q + 1Iq + 134q + I7pq — 7Iq, 57  75

33  33  1  11

• •    MB [ p, q ^]) = 4 q ⁺ 8 pq - 4 q ⁺ 64 q + -q ⁺ -pq^— —q,

• •    SDD(BT [ p, q ]) = 51 q + ^I⁹ pq — 111 q + 6 q + 13 q + 9pq — I4 q.

• < Consider the semi total point boron triangular nanotube R = BT[p, q]. There are five edge partitions corresponding to the degree of end vertices which are presented as E2,8 = {uv E Er | du = I, dv = 8}, E2,12 = {uv E Er | du = I, dv = 1I}, E8,8 = {uv E Er | du = 8, dv = 8}, E8,12 = {uv E Er | du = 8,dv = 1I} and Ei2,i2 = {uv E Er | du = 1I, dv = 1I}.

3. Boron-α nanotube, subdivision and semi total point graph of boron-a nanotube BA(X)[p, q]

Therefore, we have | E 2 , 8 | = 1I q, | E 2 , 12 | = 9 q ( q — I) , | E s , 8 | = 3 q, | E s , i2 | = 6 q, and | E 12 , 12 1 = ^3q(3p ⁸⁾ . Applying the semi total point graph operator to the Fig. 3, then respective edge partitions which edges belongs to E 2 _, 8 , E 2 _, 12 , E 8 _, 8 , E 8 _, 12 , and E 12 _, 12 respectively. Hence applying the topological indices definitions (Equation (1.1) to (1.6)), we get required results. ⊲

In this segment, we concentrated basic result on boron- α nanotube, subdivision and semi total point graph of boron- a nanotube BA(X )[ p, q ] .

Table 2. The order and size of boron- a BA(X)[p, q] nanotubes

Molecular graph	BA(X)[p,q]	S 1 = BA(X)[p,q]	R 1 = BA(X )[p,q]
Order	3 (4p + 1)	6 (29p - 4)	q (29p - 4)
Size	2 (7p - 2)	q(7p - 2)	3 q (7 p - 2) 2

Theorem 3.1. Consider the boron- a nanotube BA(X )[ p, q ] , then

• •    M 3 { BA ( X )[ p,q ] } = I pq + 4 q — 6 q + 4 q,

3    8 I 3      4     4 1I

• •    H^{{BA (} X ^)[ p, q ^{] }} =4 q ⁺ 9 q + 5 q + pq ^— 5 q + pq ^— q,

• •    F { BA ( X )[ p, q ] } = 96 q + 164 q + 104 q + 75 pq — I00 q + 1IIpq — 366 q,

I{BA(X )[ p, q ] } = 6 q + ⁸⁰ q + ²⁴ q + ¹⁵ pq - 10 q + ³³ pq

IT q

9     5     411

• •    ^m M 2 ^{{ BA ( X )[} p,q ^{] }} = -3 q ^{+ 1} q +   q + pq ^- q + pq ^{- 1} q,

16    5    12    50     25    155

• •    SDD{BA(X)[p, q]} = 6q + 41 q + 13q + 3pq - 8q + 61 pq - 61 q. 5     3                 155

• <1 Consider the boron- a nanotube H = BA(X )[ p, q ] . There are five edge partitions corresponding to the degree of end vertices which are presented as E 4 , 4 = {uv E E h | d u = 4 ,d v = 4 } , E 4 , 5 = {uv E E h | d u = 4 ,d v = 5 } , E 4 , 6 = {uv E E h | d u = 4 ,d v = 6 } , E 5 , 5 = {uv E E h | d u = 5 , d v = 5 } and E 5 , 6 = {uv E E h | d u = 5 , d v = 6 } .

Therefore, we have | E 4 , 4 | = 3 q, | E 4 , 5 | = 4 q, | E 4 , e | = 2 q, | E 5 , s | = ^q(3p2^-8) , and | E e , 6 | = 2 q ( p - 3) . The respective edge partitions are shown in Fig. 4 in which edges belong to E 4 , 4 , ^B 4 , 5 , E 4 _, 6 , E 5 _, 5 and E 5 _, 6 respectively. Hence applying the topological indices definitions (Equation (1.1) to (1.6)), we get required results. ⊲

Theorem 3.2. Consider the subdivision graph of boron- a nanotube S i = BA(X )[ p, q ] ,

• M 3 {BA(X )[ p, q ] } = 24 q + 15 pq - 30 q + 8pq - 16 q,

• H {BA(X )[ p,q ] } = 4 q + ¹⁰ pq

-

20    1

T ^{q +} 2 ^pq

-

q,

• F { BA ( X )[ p, q ] } = 240 q + 145 pq - 290 q + 80 pq - 160 q,

• I { BA ( X )[ p,q ] } = 16 q + у pq - ¹³³ q + 3 pq - 6 q,

• ^m M 2 { BA ( X )[ p,q ] } = ³ pq + ¹ q - q + ¹ pq 2      2         6

-

3 ^q,

• SDD{BA(X )[ p,q ] } = 30 q + ²⁹ pq - 29 q + у pq

-

T q.

• < Consider the subdivision graph of boron- a nanotube S i = BA(X )[ p, q ] . There are three edge partitions corresponding to the degree of end vertices which are presented as E 2 , 4 = { uv E E s i | d u = 2 , d v = 4 } , E 2 , 5 = { uv E E s i | d u = 2 , d v = 5 } and E 2 , 6 = { uv E E S ₁ | d u = 2 , d v = 6 } .

Therefore, we have | E 2 _, 4 | = 12 q, | E 2 _, 5 | = 5 q ( p - 2) and | E 2 _, 6 | = 2 q ( p - 2) . Applying the subdivision graph operator to the Fig. 4, then respective edge partitions which edges belongs to E 2 _, 4 , E 2 _, 5 and E 2 _, 6 respectively. Hence applying the topological indices definitions (Equation (1.1) to (1.6)), we get required results. ⊲

Theorem 3.3. Consider the semi total point graph of boron- a nanotube R i = ^{BA ( X )[} p,q ^] ,

• •    M 3 {BA(X )[ p, q ] } = 72 q + 40 pq - 80 q + 20 pq - 40 q + 8 q + 8 q + 4pq - 12 q,

  • •    H{BA(X)[p,q]} = 3q +1 pq - q +1 pq - 1 q + 2-q + 2-q + 2-q +-3-pq 2    2         6     3    32    10    24100

• ^- 25 q ⁺ 30 pq ⁺ 10 q,

  • • F { BA ( X ) [ p, q ] } = 816 q + 520 pq - 1040 q + 296 pq - 592 q + 384 q + 656 q

    +416 q + 300pq - 800 q + 488pq - 1464 q,

I { BA ( X )[ p,q ] }      q +²³ pq -

• 50 q + 24pq - 48 q + 12q + ^ q + 48 q 37   7     95

+ 1³ pq - 20 q + ¹³³ pq - ³³³ q,

3 111 1311

• •    ^M 2 { BA ( ^{X )[} p, ^{q ] }}    4 q + 4 pq ^- 2 q + -pq ^- 6 q +64 q +20 q +48 q

  3       1     120360

⁺ 200 pq - 25 q ⁺ ITpq - ITq

• •    SDD{BA(X )[ p, q ] } = 51 q + 26 pq - 52 q + ³⁷ pq - ⁷⁴ q + 6 q + ⁴¹ q + ¹³ q + 3pq

3       3           52

• - 8 q + ⁶¹ pq — ⁶¹ q.

• <1 Consider the semi total point graph of boron- a nanotube R i = BA(X )[ p,q ] . There are eight edge partitions corresponding to the degree of end vertices which are presented as E 2 , 8 = {uv E E r i | d u = 2 'd v = 8 } ' E 2 , i0 = {uv E E r i | d u = 2 ,d v = 10 } , E 2 , i2 = {uv E E R i ¹ d u — ² , ^d v — ^{12 }}, E 8 , 8 — ^{{ u}v ^E E R i ¹ d u — ⁸ , d v — ^{8 }}, E 8 , i0 — ^{ uv ^E E R i | d u — ^8,d v — 10 } ' E 8 , 12 — {uv E E r i | d u — 8 'd v — 12 } ' E i0 , i0 — {uv E E r i | d u — 10 ,d v — 10 } and E 10_,12 — { uv E E R _i | d _u — 10 ' d _v — 12 } .

• 4. Boron- α , subdivision and semi total point graph

Therefore, we have | E 2 , 8 | — 12 q, | E 2 , io | — 5 q ( p - 2) , | E 2 , i2 | — 2 q ( p - 2) , | E s , 8 | — 3 q, | E 8 , io | — 4 q, | E 8 , 12 | — 2 q, | E io , io | — q ¹³^- , and | E_w , i2 | — 2 q ( p - 3) . Applying the semi total point graph operator to the Fig. 4 and then applying the topological indices definitions (Equation (1.1) to (1.6)), we get required results. ⊲

of boron- a nanotube nanotube BA(Y )[ p,q ]

In this section we demonstrated the results on boron- α , subdivision and semi total point graph of boron- a nanotube nanotube BA(Y )[ p, q ] .

Table 3. The order and size of boron- a nanotubes of BA(Y )[p, q]

Molecular graph	BA(Y )[p,q]	S2 = BA(Y)[p,q]	R2 = BA(Y)[p,q]
Order	43 pq	6 (29p - 12)	6 (29p - 12)
Size	2 (7p - 4)	q(7p - 4)	3 q (7 p - 4) 2

Theorem 4.1. Consider the boron- a nanotube BA(Y )[ p,q ] , then

• •    M3{BA(Y)[p' q]} — 2q + 3q + 2q + 2q + 2pq - 5q, n 1    1    2    3    4    1     3      4     410

• •    H ^{{ BA (} Y ^)[ p^,q ^{] } —} ^ q ⁺ 4 q + 9 q +4 q + 9 q +5 q + — pq ^- 5 q ■ ~ pq ^- 44 q,

• •    F { BA ( Y ) [ p, q ] } — 9 q + 34 q + 45 q + 48 q + 82 q + 52 q + 75 pq - 200 q + 122pq - 305 q,

• •    I { BA ( Y )[ p, q ] } — ³ q + ⁷⁵ q + 2q + 3q + ⁴⁰ q + ¹² q + ⁷⁵ pq - 10 q + 60 pq - ⁷⁵³ q,

  4     8                9     5     4             1111

• •    ^m M 2 ^{{BA ( Y )[} p' q ^{] } —}    q +-1 q +³- q +   q + q + q + pq ^- q + pq ^{- 1} q'

18    15    18    32    10    24    50     25    156

• •    SDD{BA(Y)[p, q]} — q + 3-q +5q + 3q + -1 q + 13q + 3pq - 8q + 31 pq - 61 q. 15    2          10     6                 156

• < Consider the boron- a nanotube K — BA(Y )[ p,q ] . There are eight edge partitions corresponding to the degree of end vertices which are presented as E 3 , 3 — { uv E E k | d u — 3 , d v — 3 } , E 3 , 5 — { uv E E k | d u — 3 , d v — 5 } , E 3 , 6 — { uv E E k | d u — 3 , d v — 6 } , E 4 , 4

{uv E Ek | du — 4, dv — 4}, E4,5 — {uv E Ek | du — 4, dv — 5}, E4,6 — {uv E Ek | du

• 4 , d v — 6 } , E 5 , 5 — { uv E E k | d u — 5 , d v — 5 } and E 5 , 6 — { uv E E k | d u — 5 , d v — 6 } .

Therefore, we have | Е з , з | = 2 , | Е з , 5 | = q, | Е з , б | = q, | E 4 , 4 | = 3 q , | E 4 , 5 | = 2 q, | E 4 , e | = q, | E 5 , 5 | = q(³p2 8) , and | E 5 , a | = q (2 p - 5) . Hence applying the topological indices definitions (Equation (1.1) to (1.6)), we get required results. ⊲

Theorem 4.2. Consider the subdivision graph of boron- а nanotube S 2 = BA(Y )[ p, q ] ,

• •    M ₃ { BA ( Y ) [ p, q ] } = 3 q + 12 q + 15 pq — 30 q + 8 pq — 12 q,

• •    H{BA(Y)[p, q]} = 6q + 2q + 10pq — 20q + 1 pq — 3q, 5          7       7     24

• •    F { BA ( Y )[ p, q ] } = 39 q + 120 q + 145 pq — 290 q + 80 pq — 120 q,

• •    I{BA(Y)[p, q]} = 3|q + 8q + 50pq — 303q + 3pq — 9q, 5           7       72

• •    mM2{BA(Y)[p, q]} = 1 q + 3q + 1 pq — q + 1 pq — 1 q, 2    4    2          64

• •    SDD{BA(Y )[ p, q ] } = ¹³ q + 15 q + ²⁹ pq — 29 q + у pq — 10 q.

<1 Consider the subdivision graph of boron- а nanotube S 2 = { BA ( Y )[ p, q ] } . There are four edge partitions corresponding to the degree of end vertices which are presented as Е 2 , з = { uv G E S 2 | d u — ² , d v — ^{3 }}, E 2 , 4 — ^{u v G E S 2 | d u — ² , d v — ^{4 }}, E 2 , 5 — ^{ uv G E S 2 | d u — ² , d v — ^{5 }} and E 2 , 6 = { uv G E s ₂ | d _u = 2 , d _v = 6 } .

Therefore, we have | Е 2 , з | = 3 q, | E 2 , 4 | = 6 q, | E 2 , 5 | = 5 q ( p — 2) and | Е 2 , б | = q (2 p — 3) . Applying the subdivision graph operator to the Fig. 5, then respective edge partitions which edges belongs to E 2 , 3 , E 2 , 4 , E 2 , 5 and E 2 , 6 respectively. Hence applying the topological indices definitions (Equation (1.1) to (1.6)), we get required results. ⊲

Theorem 4.3. Consider the semi total point graph of boron- а nanotube R 2 = BA(Y )[ p,q ] ,

• M ₃ { BA ( Y )[ p, q ] } = 12 q + 36 q + 40 pq — 80 q + 20 pq — 30 q + 4 q + 6 q + 4 q + 4 q

+4pq — 10q, 365 52311

• •    H^{{BA ( Y )[} p, q ^{] }} = 4 q + 5 q + ^ pq ^— 3 q + 7 pq ^— 7 q + — q + 3 q

+1 q + £ q ₊ 2 q ₊ 1 q + Л pq — 2 q + A pq — £ q,

9     16    9     10    20      5     1111

• •    F { BA ( Y )[ p, q ] } = 120 q + 408 q + 520 pq — 1040 q + 296 q — 444 q + 36 q

  +136 q + 180 q + 192 q + 328 q + 208 q + 300 pq — 800 q + 488 pq — 1220 q,

n   9    48    25     50    24     36    315

• •    I^{{BA ( Y )[} p, q ^{] }} = 2 q ⁺ у q + -3- pq ^— -3- q + у pq ^— у q + ^ q + у q +4 q + 6 q + ⁸⁹ q + у q + у pq — 20 q + ¹⁹⁹ pq — ³⁹⁹ q,

  9     5     2             1111

• •    mM2{BA(Y)[p, q]} = 4q + Iq + 4pq — |q + ^^pq — 3q + у q + у q 13 113 111

⁺ 72 q 28 q ⁺ 40 q ⁺16 q ⁺ 200 pq — 25 q ⁺ 60 pq — 24 q,

• •    SDD{BA(Y)[p, q]} = 10q + 31 q + 26pq — 52q + 37pq — 37q + q + 34q 2                    3       215

  
  

  41    13

  
  
  
  

  + 2 q + 3 q +10 q + у q + 3 pq — 8 q + ^^ pq —

  
  

  q.

  
  

< Consider the semi total point graph of boron-а nanotube R2 = BA(Y)[p, q]. There are twelve edge partitions corresponding to the degree of end vertices which are presented as E2,6 = {uv G Er2 | du = 2, dv = 6}, E2,8 = {uv 6 Er2 | du = 2,dv = 8}, E2,io = {uv 6 Er2 | du =2,dv = 10}, E2,12 = {uv G Er2 | du =2,dv = 12}, Еб,б = {uv G Er2 | du = 6,dv = 6}, Еб,ш = {uv G Er2 | du =6,dv = 10}, E6,i2 = {uv G Er2 | du = 6, dv = 12}, E8,8 = {uv G Er2 | du = 8,dv = 8}, Е8,ш = {uv G Er2 | du =8,dv = 10}, E8,12 = {uv G Er2 | du = 8,dv = 12}, Eio,io = {uv G Er2 | du = 10, dv = 10} and Eio,i2 = {uv G Er2 | du = 10, dv = 12}.

Therefore, we have | Е 2 , б | = 3 q, | E 2 , 8 | = 6 q, | E 2 , io | = 5 q ( p - 2) , | E 2 , i2 | = q (2 p - 3) , ^|E 6 , 6 | = 2 , ^|E 6 , io | = q, ^|E 6 , i2 ^| = q, ^|E 8 , 8 ^| = 32 2 , ^|E 8 , io ^| = 2 q, | E 8 , i2 | = q, ^|E io , io ^| = ^q(3p2 8) , and | E io , i2 1 = q (2 p — 5) . Applying the semi total point graph operator to the Fig. 5 and then applying the topological indices definitions (Equation (1.1) to (1.6)), we get required results. ⊲

Table 4. The order and size of boron- a nanotubes of BA(Y )[p, q]

Index	G = BT [p,q]	H = BA(X)[p,q]	K = BA(Y)[p,q]
M 3	12q	[2p+2]q	[2p+4]q
H	[0.75p-0.05]q	[0.66364p+0.14798]q	[0.66364p-0.05076]q
F	[324p-456]q	[197p-202]q	[197p-235]q

Table 5. Degree based topological indices of boron nanotubes

I [13.5p-15.6]q      [9.20455p-6.67475]q    [9.20455p-9.16692]q

m M 2	[0.125p+0.10417]q	[0.12667p+0.11083]q	[0.12667p+0.08653]q
SDD	[9p-5]q	[7.06667p-1.66667]q	[7.06667p-3.13333]q

Table 6. Subdivision graph of degree based topological indices of boron nanotubes

Index	S = BT [p,q]	S1 = BA(X)[p,q]	S 2 = BA(Y)[p,q]
M 3	[36p-48]q	[23p-22]q	[23p-27]q
H	[2.25p-0.5]q	[1.92857p+0.14286]q	[1.92857p-0.40741]q
F	[360p-480]q	[225p-210]q	[225p-251]q
I	[13.5p-11]q	[10.14286p-4.28571]q	[10.14286p-7.18571]q
m M 2	0.75pq	[0.66667p+0.16667]q	0.66667pq
SDD	[30p-30]q	[21.16667p-12.33333]q	[21.16667p-17.5]q

Table 7. Semi total point graph of degree based topological indices of boron nanotubes

Index	R = BT [p,q]	R1 = BA(X)[p,q]	R2 = BA(Y)[p,q]
M 3	[90p-84]q	[64p-44]q	[64p-54]q
H	[1.66071p-0.19643]q	[0.73p+0.422083]q	[1.45087p-0.17062]q
F	[2628p-3672]q	[1604p-1624]q	[1604p-1896]q
I	[42.42857p-42.85714]q	[30.17099p-17.67330]q	[30.17099p-26.04336]q
m M 2	[0.40625p+0.02604]q	[11.25742p-32.65998]q	[0.365p+0.02163]q
SDD	[64.5p-65]q	[45.4p-25.16667]q	[45.4p-38.13333]q

Conclusion: In this paper, we study important classes of boron nanotubes and formulated M 3 , H , I , ^m M 2 , SDD indices of their molecular graphs by using edge partition technique. The simplified of these indices for boron triangular nanotube, subdivision and semi total point graph of boron triangular nanotube, boron- α , subdivision and semi total point graph of boron- a nanotube BA(X )[ p, q ] and boron- a , subdivision and semi total point graph of boron- a nanotube BA(Y )[ p, q ] are given in Table 1, Table 2 and Table 3. These results can be used in detecting some physical and chemical properties of these boron nanotubes.

Acknowledgment: The authors would like to extend their gratitude to the referee for the valuable suggestions. The first author is thankful to the Visvesvaraya Technological University, Belgaum for the financial support under TEQIP Competitive Research Grant.

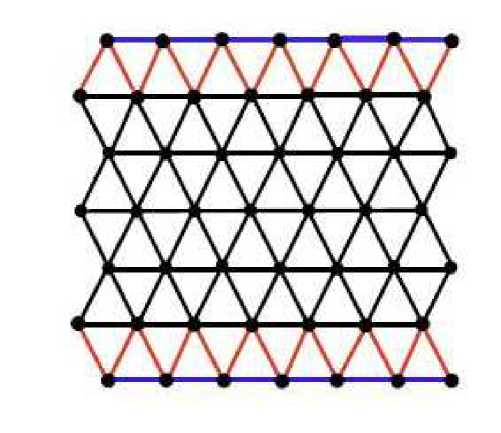
Fig. 3 The edge partitions of BT [7,4] nanotube with respect to degree of end vertices.

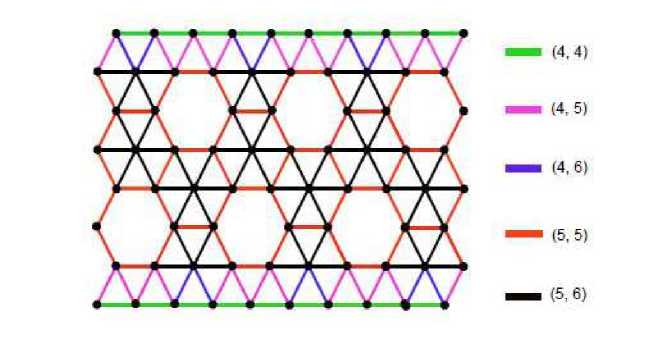
Fig. 4 The edge partitions of BA(X )[8, 6] nanotube with respect to degree of end vertices.

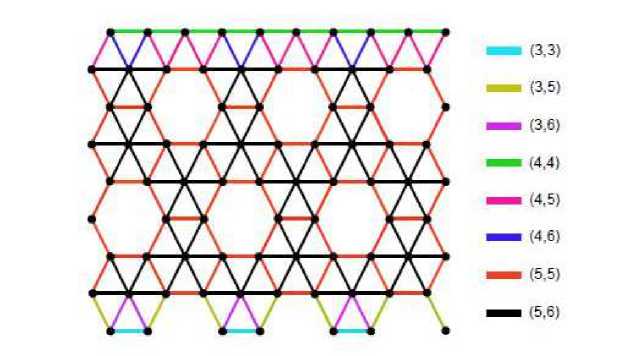
Fig. 5 The edge partitions of BT (Y)[9, 6] nanotube with respect to degree of end vertices.