Топологические солитоны в двухцепочечной модели ДНК

Интенсивные исследования последних десятилетий показали, что в нелинейных системах различной физической природы возможны коллективные возбуждения в виде нелинейных уединенных волн - солитонов. Уединенные волны обладают рядом замечательных свойств, сближающих их с частицами - сохранение формы и скорости движения после взаимодействия. Они активно применяются для описания различных кооперативных эффектов в нелинейных динамических системах, в том числе молекулярных цепочках, например, таких как ДНК [1, 2]. Особый интерес представляют квазилинейные молекулярные цепочки, характеризуемые как геометрическим ангармонизмом, так и ангармонизмом потенциала междоузельного взаимодействия. Учет этих факторов приводит к моделям, описываемым системами нелинейных дифференциальных уравнений, решение которых крайне сложно получить аналитическими методами. Это приводит к необходимости разработки методов компьютерного эксперимента для исследования динамики подобного рода систем.

В работах [3, 4] изучена динамика топологических солитонов, описывающих образование открытого состояния двойной спирали ДНК. Показано, что в двойной спирали ДНК могут появляться четыре типа топологических солитонов (см. рис. 4 из [3]). Изучены взаимодействия между солитонами, их взаимодействие с неоднородностями цепи и устойчивость солитонов по отношению к тепловым колебаниям. Основным методом работ [3, 4] был вычислительный эксперимент с использованием дискретной модели ДНК, основанный на разработанной авторами вариационной технике для нахождения солитонов. Вместе с тем такие же решения можно получить и аналитически для модели цепочек в континуальном приближении.

В данной работе использовали дискретную модель ДНК [3, 4], основанную на модели Инг-лэндера [2]. На рис. 1 схематически представлена часть данной модели. Белые и черные прямоугольники соответствуют парам оснований АТ или GC, а линии - скелету двойной спирали. Гамильтониан для этой модели имеет следующий вид:

----2----+ e2sm -----2-----+ ^^Фп,1’Фп,2) > где Г(р„д, фп2 ) = kx (1 - cos фпХ) + кх (1 - cos ри2) +^ (1 - cos(^„ д - фп2)).

Здесь ф_пХ и ф_п2 - углы поворота азотистых оснований в п-х узлах первой и второй цепочки соответственно, 1_Х и /₂ - моменты инерции оснований первой и второй цепочки соответственно, е_х и f₂ - коэффициенты упругой связи, к_х и к₂ - жесткость взаимодействия соседних оснований в одной и разных цепочках соответственно.

В основе численного метода поиска солитонного решения лежит нахождение условного минимума для лагранжиана системы с соответствующими граничными условиями [3,4]:

^,1 ⁼ ^-оо,Ь ^,2 ⁼ Ф-®,2

ФN^ ~ф®,\' Фм,1 ~Ф®,2-

Найденные точки минимума служат начальными точками для решения системы уравнений движения. Решалась система дифференциальных уравнений второго порядка (задача Коши)

d^_nj _ BH^

nX

n^

d?        Эф_пД ’

^ФпЯ - ^дН(ф_П,\Ф_П^ dt¹        дф_п^

(и = 0, ±1, ± 2...).

Интегрирование уравнений движения проводилось с помощью неявного метода Розенброка 2-го порядка точности.

Кроме численного анализа дискретной модели нами был проведен и теоретический анализ возможности получения решений с использованием теории возмущений. В континуальном приближении с учетом дисперсии длинноволновых колебаний динамика модели описывается системой двух нелинейных дифференци-

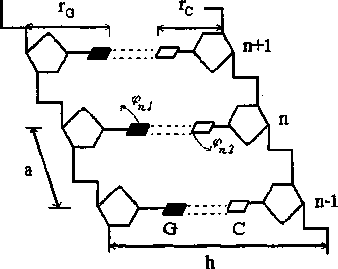
Рис. 1. Фрагмент двойной спирали ДНК, состоящей из трех пар оснований вида GC или (АТ). Расстояние между основаниями вдоль цепи а = 3.4 А, расстояние между цепями h = 16.15 А [3,4]

альных уравнений в частных производных:

1\Ф\тт ~Ч

а4 а4 2        2

^^ж-у^ ^{+ й} Ф\уу

+ к_х sin^ + к₂ sin(^ -ф^ = 0,

^гФгтт "ег

( 4            4

a и г 2 ^2^ "у ^2>у + « Ф1уу

+ X] sin ф_г -к₂ sin((9] - ф^) = 0 .

Коэффициенты перед членом с высшей дисперсией ^i^ и членом, содержащим нелинейность по пространственным производным, Ф^уФгуу при малых скоростях являются малыми. С увеличением скорости характерный размер кинков, определяемых уравнением sin-Гордон, уменьшается. В этом случае роль указанных слагаемых будет возрастать и особенно сильно проявляться именно вблизи предельной скорости солитона.

Для упрощения теоретических выкладок нами рассмотрена модель однородной молекулы ДНК, состоящей из двух одинаковых цепочек, где для простоты полагается 1_Х = /₂ = I, е_х=е_г=е. Система классических уравнений движения после перехода к новым временным и пространственным переменным путем замены т = t^Ijk_x и у = x^sa/k_x принимает вид:

Ф\« -Ф\хх-^-Ф\хххх *v^xx + sin Фх ^а^<ф_х - %) = 0,

125       2S

Фти-Ф1ХХ^ФтхФък + sin^2 -asin(^-ф^ = О, YLe       2s где безразмерный параметр a = k2/kx.

Покажем теперь, что рассматриваемая система уравнений допускает аналитические решения, подобные полученным в работе [3] в ходе численного эксперимента.

Решения будем искать в виде ряда

Ф\ = Фо + Ф\ + ^₂ + •••» Фг = Фо + h + Ч> + -, где (Э_о - решение системы, не учитывающей взаимодействие цепочек. Без учета взаимодействия цепочек (при а = 0) рассматриваемая система приводит к известному уравнению sin-Гордон, решение которого в виде 2л- -кинка имеет вид

Ф_о = 4arctgexp(z), где z = (1— s²)^-^²^, 5 - скорость солитона, ^ = x-st. Подставляя решение в виде ряда в рассматриваемую систему, получим в первом приближении уравнения для возмущений ф_х и v_x:

Ф\ "Фх +^1008(90 --Г-Фохххх + ^Ф0хФ0хх=Ь’

Y2s 2s

Ч "Ч + Ч COS% ""Фохххх + ^^0хх = °. 12s 2s

Математика

где cos % = 1 - 2/ch2 z. Полученная система уравнений имеет следующее решение:

С, к, ⁺? thz-ik „      15г, thz

—=---!---- I-----------edkA--!-- chz 24s(l-s2)2^^^^)^^      12^(1-52)2 chz’

+? th.z-ik „      15r, thz у, = —1------------г— e dk +---------, chz 24^(1-?)2 _i(i + fc2)ch^ 12s(l — s2)2 ch z где С] и C2 определяются из условия разрешимости уравнений для возмущений второго порядка малости (в нашем случае Q = О и С2 = 0). Эти константы определяют сдвиг кинков друг относительно друга. В нашем приближении этот сдвиг не удается получить аналитически. Таким образом, взаимодействие цепочек изменяет только форму кинка.

Общий вид полученного решения представлен на рис. 2 и качественно соответствует случаю (е) на рис. 4 [3]. Заметим, что при приближении скорости солитона к предельной ( з —> 1) теория возмущений дает большие погрешности.

Солитонное решение задачи можно охарактеризовать топологическим зарядом q = (^_ь д₂), где q, = (^оо,, "  Ф®,, )/2 л^- О' = 1,2) является целым числом (^,=0, ±1, ±2,...). Для нахождения солитонного решения с топологическим зарядом q нужно решить задачу на минимум с граничными условиями:

Ф-® д ⁼ ^-00,2 ⁼ 0’ ^00,1 ⁼ 2л^, <р_{т г} = 2лq₂-

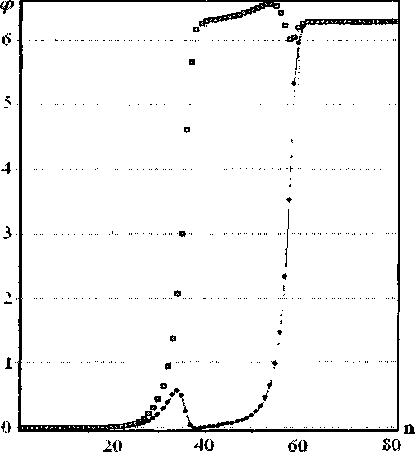
При компьютерном моделировании стационарных солитонов с топологическим зарядом q = (1, 1) получены результаты, представленные на рис. 3.

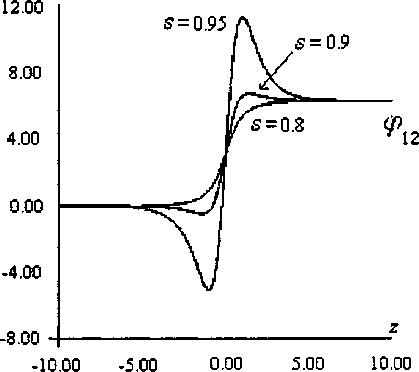
Рис. 2. Вид стационарных солитонов с топологическим зарядом q = (1,1) при различных значениях безразмерной скорости солитона

[-..$i-..$U

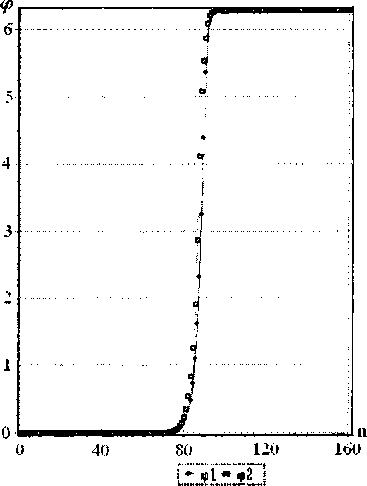
Рис. 4. Вид стационарного солитона с топологическим зарядом q = (1,1) при скорости s = 0,804. К = 0,234 Н/м. Ширина 25 звеньев в каждой цепочке. Тип оснований GC

Рис. 3. Вид стационарного солитона с топологическим зарядом q = (1,1) при скорости s = 0,592. К = 0,234 Н/м. Ширина 27 звеньев в каждой цепочке. Тип оснований GC

Закирьянов Ф.К., Хамзин С.Р., Топологические солитоны Юлмухаметов К.Р. в двухцепочечной модели ДНК

Видно, что происходит сдвиг кинков между двумя цепочками, то есть в одной из цепи кинк уходит немного вперед относительно другого кинка. Анализ показывает, что такой сдвиг происходит не при всех параметрах цепочки и скоростях уединенной волны, в частности, можно задать параметры таким образом и выбрать скорость солитона так, что сдвиг будет отсутствовать на всем протяжении движения солитона по цепи (рис. 4). Данный сдвиг объясняется неоднородностью цепи - у разных пар азотистых оснований различные параметры взаимодействия, масса и инерция, которые влияют на повороты углов в цепи. В случае теоретического исследования сдвиг отсутствует, так как рассматривалась только однородная цепочка (рис. 2). Представленная на рис. 4 динамика кинков без сдвига, имеет хорошее соответствие с аналитическими результатами.

Зависимость энергии топологического солитона q = (1, 1) от его скорости, полученная аналитически, представлена на рис. 5 (.Ei). В ходе численного эксперимента была получена зависимость безразмерной энергии топологического солитона (Е) от безразмерной скорости (s) для всех трех интересующих нас типов топологических зарядов q = (1, 1) , q = (1,0) и q = (О, 1), которая представлена на рис. 6.

800 "1 кДж/'моль

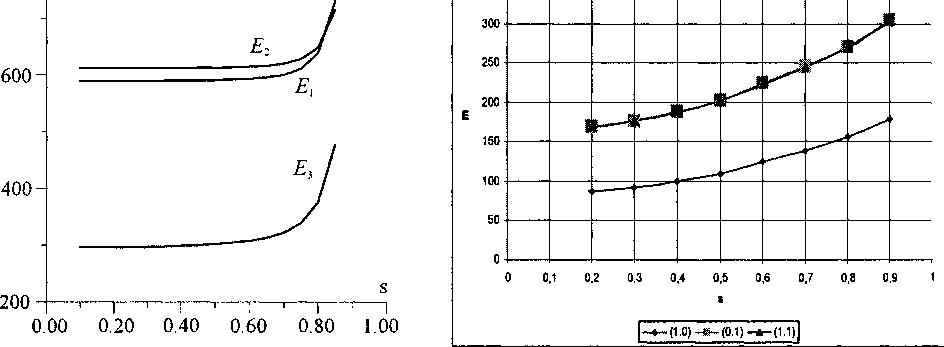
Рис. 5. Зависимости энергий стационарных солитонов с топологическими зарядами q = (1, 1) - Ei, q = (1, -1) - Е_г и q = (1, 0) - Е₃ от безразмерной скорости s (*i/e = 0,1,о = 0,1)

Рис. 6. Графики зависимости безразмерной энергии топологического солитона (А) от безразмерной скорости (s), для оснований GC

Видно, что графики зависимости безразмерной энергии от безразмерной скорости для топологических солитонов q = (1, 0) и q = (0, 1) практически совпадают, так же как и при аналитическом решении.

Для получения аналитических решений, описывающих солитоны с топологическим зарядом q = (1, -1), используем разложение

Ф\ = Фо + V\ + ^2 + Ф1 = "Фо + И + ^2 + -, при этом в первом приближении получим для возмущений следующую систему уравнений: ^1 -y"*^ cospo --^-Фохххх ^^ФохФохх + «sin(2^₀) = О , 12г 2е

Ч - ч"+ч cos % —^-ф_Охххх ^^ФохФохх -asin(2%) = 0. 12г 2г

Её решение в виде стационарных волн имеет вид

^1 =

15К] 12s(l-s²)²

-2а --+ а- chz

^1

th z-ik

4 =

15^ 12s(l-s²)²

+ 2a--a + Jchz .

24=(l-s2)2}2(1+Ji2)ch^

кх          thz-ik

eifadk,

24=(l-s2)2J2(H-li2)ch^

eitedk.

Математика

В итоге ф_х и р₂ имеет солитонные решения с топологическим зарядом q = (1, -1), представленные на рис. 7 и качественно соответствующие случаю (ж) на рис. 4 [3]. Зависимость энергии топологического солитона q = (1, -1) от скорости солитона представлена на рис. 5 (£₂)-

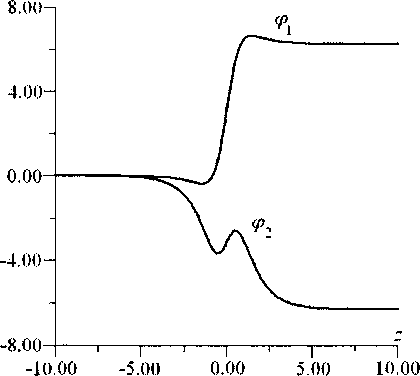
Рис. 7. Вид стационарного солитона с топологическим зарядом q = (1,-1) для значения безразмерной скорости s = 0,9

Решения, полученные численно, и представленные на рис. 8, имеют качественное сходство с аналитическими решениями (рис. 7). Отличие их связано с упомянутым выше влиянием неоднородности цепочек, приводящим к расхождению кинков с течением времени.

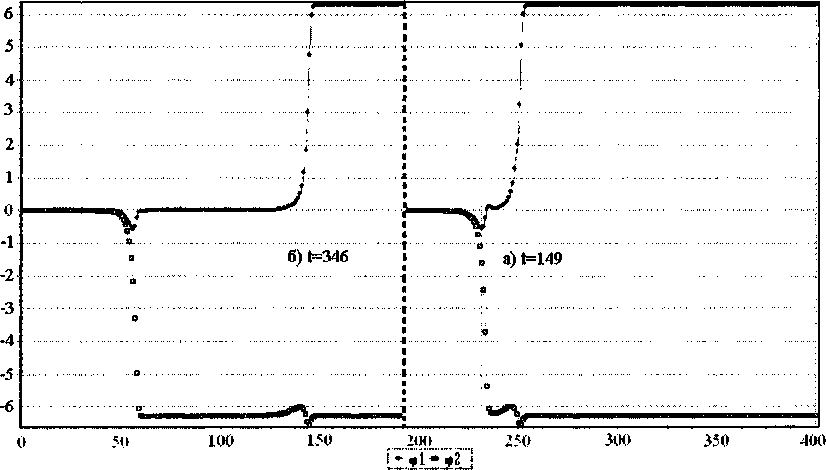
Рис. 8. Вид стационарного солитона с топологическим зарядом q = (1,-1), в разное время численного эксперимента (t- время в программе). Скорости s = 0,898. К = 0,234 Н/м. Ширина 32 звена в каждой цепочке. Тип основания GC. Солитон движется справа налево

Солитоны с топологическими зарядами q = (1, 0) и q = (0, 1) будем считать практически эквивалентными, поскольку они соответствуют одной физической ситуации распространения кинка по одной цепочке, сопровождаемого малым возмущением по другой цепочке. Отличие будет только в значениях энергий рассматриваемых солитонов. Решение рассматриваемой модели в данном случае ищется в виде разложения:

Ф\ = 9»*V\^Vi*-^ Ф₂=у_х+у₂+.„,

В первом приближении для возмущений \у_х и v_x имеем систему уравнений:

Ух -Ух+Ух cosp₀ -5-<р_0хххх +^^_Олх + asin(p₀) = 0, 12s 2s

• V, -V] + v_T --7-ф_Охххх ^Mta -asm(%) = 0 . 12г 2s

Полученная система уравнений имеет следующее решение: Зк, thz fl                     thz-ik „

V_x= ---Ц-т----а +--------- r—edk

¹ 2s<\-sb²^z (2   24г(1-г²)²)_^_{(1 +} ^.2_)сЬ^

^1 =

Зк_х thz f к\ 6£(1-S²)²chz (65(1-S²)²

-2a (shzln(2chz)-zchz).

Таким образом, взаимодействие цепочек изменяет только форму кинка, вид которого представлен на рис. 9, качественно соответствующем случаям (а-г) на рис. 4 [3]. Численное моделирование (рис. 10) указывает на хорошее качественное соответствие с полученными аналитически результатами. Зависимости энергии топологического солитона q = (1, 0) от его скорости, полученные аналитически и численно представлены на рис. 5 (Дз) и рис. 6.

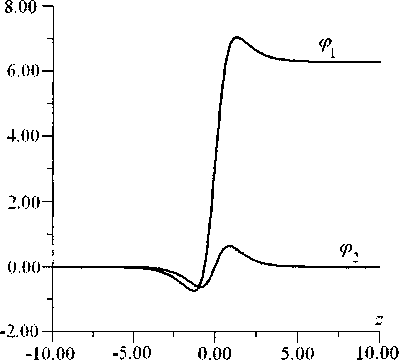
Рис. 9. Вид стационарного солитона с топологическим зарядом q = (1,0) для значения безразмерной скорости s = 0,9

Таким образом, теоретический анализ рассматриваемой модели однородной ДНК показал, что в системе могут быть решения в виде солитонов со следующими топологическими зарядами:

• 1)    q = (1, 0) (или q = (0, 1)) (по одной цепочке распространяется возмущенный кинк, а по второй

  

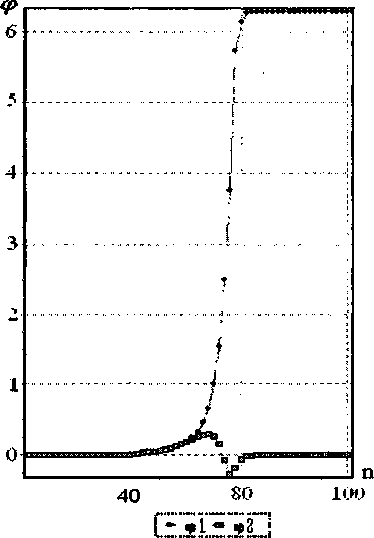
  Рис. 10. Вид стационарного солитона с топологическим зарядом q = (1,0) при скорости 5 = 0,901. К = 0,8714 Н/м. Ширина 19 звеньев цепи. Тип основания GC

  
  

цепочке - малое возмущение), соответствующие локальным движениям, возникающим при транскрипции ДНК;

• 2)    q = (1, 1) (по двум цепочкам распространяются в одном направлении и с одинаковыми скоростями два одинаковых возмущенных кинка), который соответствует переходу ДНК из одного конформационного состояния в другое;

• 3)    q = (1, -1) (по двум цепочкам распространяются кинк и антикинк), который описывает процесс репликации ДНК.

Получены зависимости энергии топологических солитонов от безразмерной скорости s. При этом энергетически наиболее выгоден солитон с топологическим зарядом q = (1, 0) (рис. 5, 6). Проведено сравнение результатов численного и аналитического решений. Результаты показывают, что решения, полученные аналитическим методом и численным экспериментом, имеют качественное сходство.

Математика

Авторы выражают искреннюю благодарность профессору М.А. Шамсутдинову за полезные обсуждения в ходе выполнения работы.