Топологическое описание образования кротовых нор в общей теории относительности

О кротовых норах в пространстве-времени специалисты по общей теории относительности много писали первоначально с 1950-х в связи с моделью электрического заряда, предложенной Уилером [1], затем с 1987 года, обсуждая модель машины времени, описанной Торном с совторами [2]. В обоих случаях речь шла о 3-мерных кротовых норах - своеобразных туннелях в 3-пространстве, искусственное образование которых нарушала односвязность пространства и требовала экзотической материи в качестве источника.

Однако, еще в 1982 году в наших статьях [3,4] было предложено создавать 4-мерные кротовые норы, которые нарушали связность 3-пространства, с целью сверхбыстрых перемещений во Вселенной или возврата в прошлое.

Образование кротовых нор с точки зрение топологии означает произведение топологических перестроек 3-пространства за счет приклеивания 4-ручек S3 х [0,1] к 4-мерному пространству-времени в случае 4-мерной кротовой поры, или приклеивание 3-ручки S2 х [0,1] к 3-мерному физическому пространству в случае 3-мерной кротовой норы (см. рис. 1, 2).

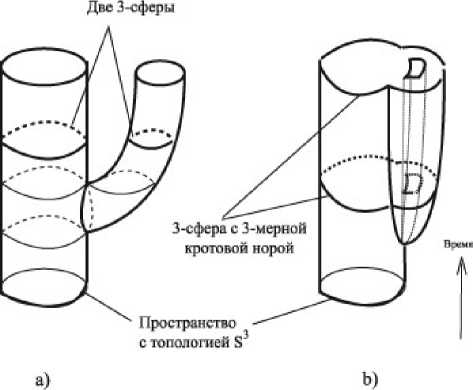
Рис. 1. а) Потеря связности 3-пространства с топологией 3-сферы. Образуются два 3-пространства, каждое из которых гомеоморфно 3-сфере; Ь) Потеря односвязности 3-пространстве с топологией 3-сферы. Имеем одно 3-пространство.

В работах [3,4] изучалась проблема разрыва 3-мерного риманова пространства. Показывалась роль потери непрерывности первых производных римановой метрики на поверхности разрыва. Как этот процесс описывается за счет изменения топологии, было показано в статьях [5,6].

В данной статье мы представляем усовершенствованную конструкцию образования кротовых нор, использующую изменяющееся во времени семейство топологий с конечной потерей непрерывности производных метрики, приводящее в итоге к пространству-времени с 3-мерной или 4-мерной кротовой норой.

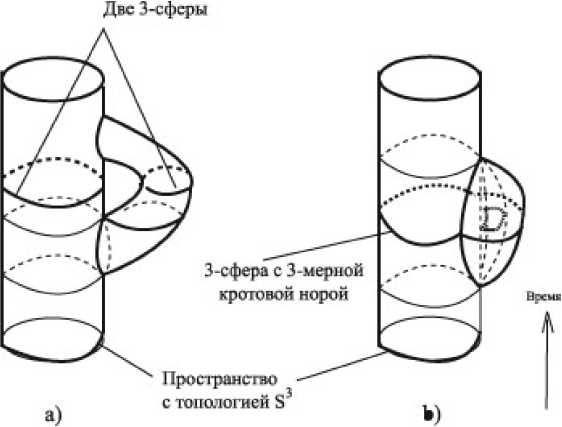
Рис. 2. а) Рождение 4-мерной кротовой норы. Пространство с топологией 3-сферы теряет связность. Образуются два пространства, каждое из которых гомеоморфно 3-сфере; Ь) Рождение 3-мерной кротовой норы в пространстве с топологией 3-сферы. Пространство теряет односвязность.

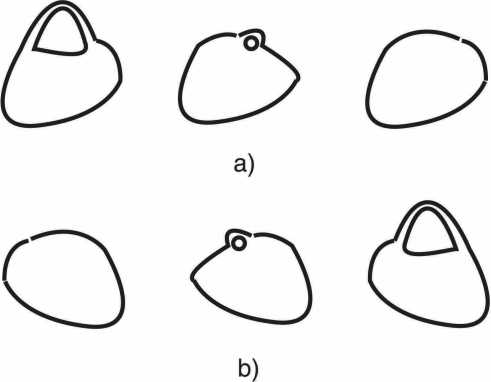
Рис. 3. а) Исчезновение 3-мерной кротовой норы, или 3-ручки; Ь) Рождение 3-мерной кротовой норы, или 3-ручки.

Для реализации описанной модели образования ручки рассмотрим параметрическое семейство функций s_t (г), 力 G [0 , 1], т G [0 , +8 ) , такое, что для любого г G [0 , +м)

s o (г) 三 1,   st (0) = 1,

lim st (г) = 1

『 一 + 为

и при г е (0, +8)семейство функций st представляет непрерывную деформацию функции s0 в функцию s1, причем все st (ж) непрерывны вместе с первыми производными. Единственной функцией, производная которой имеет разрыв первого рода в точке г = 1 является s1 (ж) (см. рис. 4 (Ь)). Наконец, пусть lim s’ (г) = —1,

И-0 1' 丿

lim 丁 一 1+0

^s 1 ^(г)

=+1.

Рассмотрим топологическое подпространство rt = {(『,32),5% (г), st (г 土 0)} с индуцированной топологией пятимерного арифметического пространства R5, где s%(г 土 0)=

lim р — 『 ± 0

6t ( р )・

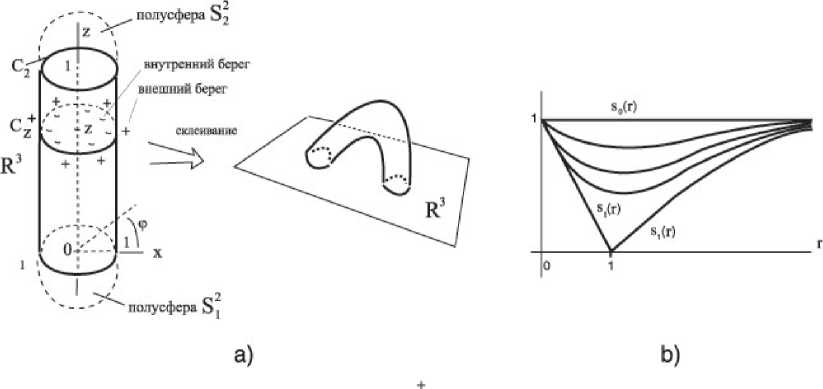
Рис. 4. а) Метаморфоза цилиндра Z; Ь) Графики функций s%(r), 力 С [0 , 1] .

Две точки ((r,g,z),Q,Q ) и ((r‘,d,z'),b,/3) пространства Г± назовем эквивалентными тогда и только тогда, когда, во-первых,

• 1)    (r,R z) = (r',d,z‘); 2) а = 6; 3) lim s^p) = lim /7(р); ртт— 0        ртт +0

и, во-вторых,

• 1)    г = 1, 0 < “ ， д < 2тт, z‘ = z (0 < z, z‘ < 1); 2) а = 6; 3) (а = В = lim s ； (p) = -1); p_ 1 — о и, в-третьих,

• 1)    г = 1, 0 < “ ， g < 2тт, z‘ = z (0 < z, z‘ < 1); 2) а = 6; 3) (а = В = lim s](p) = +1).

• —     —          .—     —                         p_ 1+0

Профакторизуем пространство Г] по введенному отпошению эквивалентности 〜. В результате при при t = 1 прострапство R³ превращается в многообразие с ручкой, т.е. в неодиосвязное некомпактное 3-многообразию с 3-мерной ручкой, которую физики называют 3-мерной кротовой норой (см. рис. 3 (Ь)).

1.1.    Изменение геометрии

Зададим семейство римановых метрик

山2 = Л2(г, z)[dr2 + dz2]+ г2 [В] (г, z)]—2dg2, отражающих изменение геометрии по мере изменения топологии, где функции 4, В] выбираются так, что, во-первых, при t < 1 они С 2-гладкие и, во -вторых, при t = 1 имеем:

lim А] =  lim А],   lim В] = lim В] при 0 < z < 1                  (1)

11+0    11 — 0    11+0    11 — 0

И

А] (1,z)[B] (1,z)]—1 т 0 пр и t т 1 — 0 (0 < z < 1).

Последнее условие — это геометрическое отражение условия стягивания окружностей С1, C_z , С2 в точку, при котором их длина должна стремиться к нулю.

Более точным, вместо условий (1) было бы условие наличия разрыва конечного скачка у (функции В] по перемешюіі г： дВ]        дВ]

lim —— = lim —— піш 0 < z < 1.                        (2)

• ■т1+0 дг   гт1 —0 dr

2.    Процесс разрыва 2-мерной поверхности на два «куска»

Это говорит о нарушении гладкости, как компонент тензора кривизны, так и тензора Риччи. Если принять, что риманово многообразие замкнутое (или провести его компактификацию), и использовать формулы типа Гаусса-Бонне-Черна [9], например формулы Ревентоса (см. в [9]), то это будет говорить о том, что при 力=1 за счет разрыва кривизны меняется одно из чисел Бетти, а，точнее. pi(M3). ііііыміі словами, образуется ручка.

1.2.    Физическая интерпретация

С точки зрения описания динамики образования ручки в 3-пространстве M3 (на языке физиков -кротовой норы) в пространстве-времени с метрикой d/2 = A^r, z)[dr2 + dz2] + r2[0(r, z)]-2dg2 - [0(r, z)]2必2, условие (2) означает появление 5-функции 8(r) в правой части вакуумных уравнений Эйнштейна, трактуемое как включение источника энергии на границе цилиндра Z в момент времени 力=1. Именно этот приток энергии и меняет топологию 3-мерного пространства, делая ее неодносвязной.

Посмотрим как можно осуществить топологическую перестройку на примере отрыва «куска» 2-мерной поверхности, избегая введения дополнительных функций 6 占 которые никак не связаны с геометрией разрываемого пространства. Будем исправлять этот недостаток, заменяя функцию ft на метрику поверхности, точнее, на коэффициенты 1-й квадратичной формы Е, F, G:

ds² = ^2 Qabd^ du^ = е (n,v)du2 + 2F (u, v)dudv + G(u, v)dv². a,b=1

Точнее, мы сочетаем идею изменения топологии, описываемой разрывами производной функции st, с идеей замены st на компоиеиты метрики Qab [Ю].

Пусть дана поверхность S, а на ней жорданова гладкая кривая L. Читатель может представить себе для лучшего понимания, что разрывать будем двумерную сферу по экватору L. Рассмотрим гладкое векторное поле 。， интегральные кривые которого исходят из точки (северный полюс сферы) вне кривой L и приходят в точку внутри кривой L (южный полюс), трансверсально пересекая L. Отметим, что, как будет видно из дальнейшего, для нас важным является происходящее в окрестности кривой L, и прочие точки поверхности не играют никакой роли. Для любой точки т из S можно вычислять предел производной метрики по проходящей через точку т интегральной кривой поля 。 с двух сторон — «справа» —0 и «слева» -0. Мы полагаем, что метрика в момент разрыва такова, что эти производные равны везде, кроме точек кривой L (т.е. кроме точек экватора).

Вводим условие:

U : пределы производной метрики по проходящей через точку т интегральной кривой поля 。 с двух сторон - «справа» +0 и «слева» —0 равны.

Говорим, что точки т,д е S эквивалентны, т.е. т 〜 д, если т = д, и выполнено условие U.

Если для времени 力 е [0 , 1) все компоненты метрики имеют гладкие производные, то фактор-пространство St = S/ 〜 гомеомор 小 тю поверхности S ii состоит из одной компоненты связности. Но если при 力 =1 проігзводиые метрики тіетот разине пределы «справа» ii «слева» на кривой L (на экваторе), т.е. условие U не выполняется, то фактор-пространство Si = S/ 〜 имеет уже две компоненты связности. Иначе говоря, мы разрываем поверхность на два «куска» К° = S \ int(K) ii K (рис. 5).

В нашем примере со сферой при 力 =1 точки на экваторе раздваиваются на северные точки (пределы -0) и на южные точки (пределы +0). Рождаются две полусферы с краями, состоящими из северных точек экватора и соответственно - южных точек экватора. Можно теперь отождествить все северные точки, и отдельно все южные точки, и получить две сферы. Иначе говоря, имеем

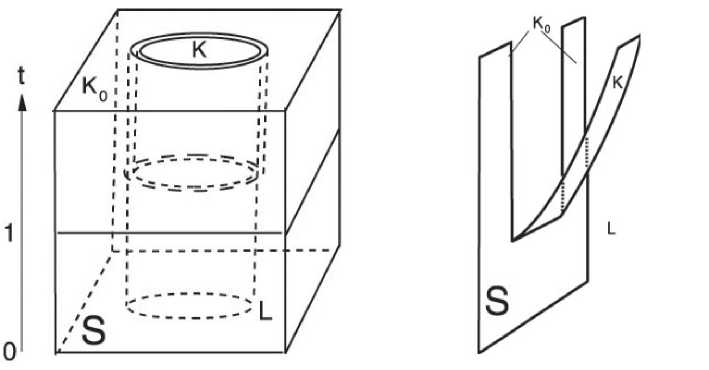
Рис. 5. Разрыв поверхности S на два куска К° и К по L. Слева 2-мерный случай, справа -1-мерный.

процесс отрыва южного полушария с последующим затягиванием краев разрыва в точки: получаем две сферы. С точки зрения топологии процесс безупречен, но возникает проблема с определением метрики на стянутых краях (см. § 1.1).

Математически образование ручек в 3-мерном многообразии достаточно подробно описано в рамках дифференциальной топологии. Но эти описания плохо удовлетворяют потребностям практической геометрии и особенно потребностям тех, кто работает в области общей теории относительности, являющейся теорией пространства-времени. Необходимо иметь достаточно простую конструкцию образования ручки в 3-мерном пространстве как с точки зрения топологии, так и с точки зрения геометрии.

3.    Отрыв области от риманова 3-пространства

Как показано в § 2, при решении задачи увеличения число компонент связности в 2-мерном случае можно избавиться от дополнительных функций s_t и использовать для задания желанной топологии, непосредственно метрику поверхности. Перенесем этот метод на 3-мерный случай. В результате мы по-новому опишем рождение 4-мерной кротовой норы, или 4-ручки, изображенное на рис. 2 (а).

Осуществим отрывание компактной области К с гладкой 2-мерной границей дК ) находящейся в 3-мерном римановом пространстве М 3.

Пусть то е К - точка, лежащая внутри области К. Из нее выпустим непересекающиеся кривые %, проходящие через каждую точку г е S трансверсально к дК.

На 3-многообразии М³ зададим семейство римановых метрик h_a^ (。， t е [0,1], такое, что һ&в (t) при 0 < t < 1 — С¹-гладкое тензорное поле, а при t = 1 оно имеет разрывы производных первого рода на границе дК замкнутой области К вдоль кривых 入乞.

Вводим условие:

U :пределы производной метрики по проходящей через точку г е S кривой 入 乞 с двух сторон - «справа» +0 и «слева» —0 равны.

Говорим, что точки х,у е М³ эквивалентны, т.е. т 〜 д, если т = ди выполнено условие U.

Для t е [0,1) все компоненты метрики иметот гладкие проігзводиые. следовательно (фактор-пространство Mt = М3/ 〜гомеомор(1)ію пространству М3 ii состоит из одной компоненты связ-ІІОСТІІ. Но при t = 1 проігзводиые метрики имеют разине пределы «справа» ii «слева» на кривой А (на грашш.е S). т.е. условие U не выполняется, ii поэтому 小актор-пространство М3 = М3/ 〜 имеет уже две компоненты связности. Иначе говоря, мы разорвали пространство на два «куска» К и К。= М3 \ int(K).

В данном параграфе мы реализовали ситуацию, изображенную на рис. 2 (а). Точки поверхности S при 力 =1 раздваиваются на «северные» точки (пределы -0) и на «южные» точки (пределы +0). Ро7кда ， тотся два. отдельных 3-мерных мііогогообра ： зпп с краем.

Можно теперь отождествить все «северные» точки, и отдельно все «южные» точки, и получить два многообразия без края.

Как уже говорилось, процесс безупречен с точки зрения топологии, но возникает упомянутая выше проблема с определением метрики на стянутых краях.

Вполне понятно теперь, что описанный метод можно применить и для случая рождения 3-мерной кротовой норы.

4.    Оценка затрат энергии на образование кротовой норы

Оценить энергию, необходимую для образования кротовой норы (ручки), можно с помощью одной из формул типа Гаусса-Бонне-Черна (см. [9]).

Примем, для простоты вычислений, что пространство-время является замкнутым ориентируемым многообразием < М4,д > сигнатуры < +---->.

Тогда имеет место формула (см. [9], (1.2)):

m4

w_iklm 爪法以壶

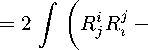
м 4

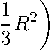
dv — 8 冗 2х(М 4),

где %/ki — тензор Вейля,

Х ( М⁴ ) = £ ( -1 )飴 k(M⁴ )

k=0

• —характеристика Эйлера-Пуанкаре многообразия М 4, а /к(М4) — ^-мерное число Бетти.

Появление 4-мерной ручки, изображено на рис. 2 (а), 3-мерной - на рис. 2 (Ь). При этом мно-гс 〉 с 〉 ора ： зііе М⁴ превраш,ается в мтюгоооравііе М⁴ ii меняются соответ*. твут ( . ) ттпіе qiicna Бетти. ІІнаііе говоря

Sx = х(М4) - х(М4) = 0.

Можем написать, что

■---, м 4

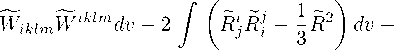
■---, м 4

м 4

W_MmW^lklmdv + 2 / (写留- 3^2^ dv = 8/Sx. м ⁴

В случае, например комфорно плоских метрик, тензор Вейля обнуляется и

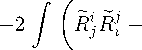
必 ⁴

3 后 2 ) dv + 2 / (招叫- м ⁴

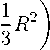
dv = 8 冗 ²Sx.

Поскольку тензор Риччи выражается с помощью уравнений Эйнштейна через тензор энергии- импульса

R2k = к (gk - 292kT), или ДЛЯ 7；k = EUzUk, g2kUgUk = 1,

R2k = к

(EUgUk -

2 92k £

,

то формулу (3) можно символически записать как

呂 ² у* (5e)²dv

в4

8тт 2 Ьх,

где 呂一 некоторая ( {ягзическая константа.

Следовательно, имеем для среднего значения скачка плотности энергии £, влекущего образование кротовой норы:

仅庁〉= ^28^ б»

Здесь В4 -множество-носитель топологической, гладкой и метрической структур пространств-времен М4 ii М4： м4 =<В4, 丁, g,g>,   М4 =< В4, f, §,g >, из которых мы в данной статье сконцентрировали внимание только на метаморфозе топологической структуры, предложив конструкцию возникновения кротовых нор.

Заключение

Нам удалось максимально просто описать процесс топологического образования кротовой норы, используя только термины, относящиеся к геометрии пространства. Предлагаемая конструкция, как мы отмечали, более доступна для восприятия физиками, чем конструкция, предложенная Коморовским [7].

Также, мы представили схему вычисления затрат энергии, требуемой для образования кротовой норы, которую, конечно, крайне сложно реализовать, но во всяком случае мы видим путь, идя по которому можно такие вычисления проводить.